ОБЛАСТЬ ТЕХНИЧЕСКОГО ПРИМЕНЕНИЯ
Настоящий документ относится к системам кодирования источника звука. В частности, настоящий документ относится к системам кодирования источника звука, использующим линейное предсказание в сочетании с набором фильтров.
ПРЕДПОСЫЛКИ
Есть два важных инструментальных средства обработки сигналов, применяемых в системах кодирования источника звуковых сигналов, а именно: наборы фильтров с критической дискретизацией и линейное предсказание. Наборы фильтров с критической дискретизацией (например, наборы фильтров на основе модифицированного дискретного косинусного преобразования, MDCT) делают возможным прямой доступ к частотно-временным представлениям, где можно использовать перцепционное несоответствие и избыточность сигнала. Линейное предсказание делает возможным эффективное моделирование источника звуковых сигналов, в частности в речевых сигналах. Сочетание этих двух инструментальных средств, т.е. использование предсказания в подполосах набора фильтров, главным образом, было использовано для кодирования звука с высокой битовой скоростью передачи данных. Для кодирования с низкой битовой скоростью передачи данных проблемой, связанной с предсказанием в подполосах, является поддержание низких издержек (т.е. битовой скорости передачи данных) для описания предсказателей. Другой проблемой является управление ограничением результирующего шума сигнала ошибки предсказания, получаемого предсказателем подполос.
В US2006/0015329 A1 описан способ кодирования звука, в котором применяют устройство для синтезирования форм волн для генерирования набора предсказанных дискретных значения звукового сигнала.
Возможным путем решения проблемы кодирования описания предсказателя подполос эффективным с точки зрения количества битов образом является оценка предсказателя исходя из ранее декодированных частей звукового сигнала и полностью избегать, таким образом, издержек описания предсказателя. Если предсказатель можно определить исходя из ранее декодированных частей звукового сигнала, то предсказатель можно определить в кодере и в декодере без необходимости в передаче описания предсказателя из кодера в декодер. Эта схема именуется адаптивной схемой предсказания в обратном порядке. Однако адаптивная схема предсказания в обратном порядке, как правило, значительно ухудшается при уменьшении битовой скорости передачи данных кодированного звукового сигнала. Одним из альтернативных или дополнительных путей к эффективному кодированию предсказателя подполос является выявление более естественного описания предсказателя, например описания, использующего структуру, внутренне присущую подлежащему кодированию звуковому сигналу. Например, кодирование речи с низкой битовой скоростью передачи данных, как правило, применяет адаптивную схему в прямом порядке, основанную на компактном представлении краткосрочного предсказателя (использующего краткосрочные корреляции) и долговременного предсказателя (использующего долгосрочные корреляции, обусловленные основным тоном, лежащим в основе речевого сигнала).
Для решения проблемы управления ограничением шума сигнала ошибки предсказания было сделано наблюдение того, что несмотря на то, что ограничением шума предсказателя можно хорошо управлять внутри подполосы, окончательный выходной звуковой сигнал кодера, как правило, проявляет артефакты паразитных частот (за исключением звуковых сигналов, проявляющих по существу плоскую форму спектрального шума).
Важным случаем предсказателя подполос является реализация долгосрочного предсказания в наборе фильтров с перекрывающимися окнами. Долгосрочный предсказатель, как правило, использует избыточности в периодических или близких к периодическим звуковых сигналах (таких как речевые сигналы, проявляющие внутренне присущий им основной тон), и его можно описать единственным параметром предсказания или небольшим количеством таких параметров. Долгосрочный предсказатель можно определить в непрерывном времени посредством задержки, отражающей периодичность звукового сигнала. Когда эта задержка велика в сравнении с длиной окна набора фильтров, долгосрочный предсказатель можно реализовать в области дискретного времени посредством сдвига, или дробной задержки, и можно преобразовать обратно в причинный предсказатель в области подполос. Такой долгосрочный предсказатель, как правило, не проявляет артефакты паразитных частот, но здесь существует значительный штраф в вычислительной сложности, вызванной необходимостью в дополнительных операциях набора фильтров для преобразования из временной области в область подполос. Кроме того, подход, заключающийся в определении задержки во временной области и преобразовании задержки в предсказатель подполос, не применим в случае, когда период подлежащего кодированию звукового сигнала сравним или не превышает размер окна набора фильтров.
Настоящий документ направлен на вышеупомянутые недостатки предсказания подполос. В частности, настоящий документ описывает способы и системы, делающие возможным эффективное с точки зрения битовой скорости передачи данных описание предсказателей подполос и/или делающие возможным уменьшение артефактов паразитных частот, вызываемых предсказателями подполос. В частности, способ и системы, описываемые в настоящем документе, позволяют реализовать аудиокодеры с низкой битовой скоростью передачи данных, использующие предсказание подполос, вызывающее пониженный уровень артефактов паразитных частот.
КРАТКОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ
Настоящий документ описывает способы и системы, улучшающие качество кодирования источника звука с применением предсказания в области подполос набора фильтров с критической дискретизацией. Эти способы и системы могут использовать компактное описание предсказателей подполос, причем описание основано на моделях сигнала. В качестве альтернативы или в дополнение, способы и системы могут использовать эффективную реализацию предсказателей непосредственно в области подполос. В качестве альтернативы или в дополнение, способы и системы могут использовать члены межполосного предсказателя подполос, описываемые в настоящем документе, для того чтобы сделать возможным уменьшение артефактов паразитных частот.
Как описывается в настоящем документе, компактное описание предсказателей подполос может содержать частоту синусоиды, период периодического сигнала, немного негармонический спектр, встречающийся при колебании жесткой струны, и/или множество тонов для полифонического сигнала. Показано, что в случае долгосрочного предсказателя периодическая модель сигнала обеспечивает высококачественные причинные предсказатели для интервала параметров запаздывания (или задержек), включающего значения, являющиеся более короткими и/или более длинными, чем размер окна набора фильтров. Это означает, что периодическую модель сигнала можно эффективно использовать для реализации долгосрочного предсказателя подполос. Предусмотрен плавный переход от предсказания на основе синусоидальной модели к приближению произвольной задержки.
Непосредственная реализация предсказателей в области подполос делает возможным доступ в явном виде к воспринимаемым характеристикам вырабатываемых искажений квантования. Кроме того, реализация предсказателей в области подполос делает возможным доступ к таким численным свойствам, как коэффициент передачи предсказания и зависимость предсказателей от параметров. Например, анализ на основе модели сигнала может выявить, что коэффициент передачи предсказания является значимым лишь для подмножества рассматриваемых подполос, а изменение коэффициентов предсказателя в зависимости от параметра, выбранного для передачи, может быть полезно при проектировании форматов параметров, а также эффективных алгоритмов кодирования. Более того, вычислительную сложность можно значительно снизить по сравнению с реализациями предсказателей, полагающимися на использование алгоритмов, действующих как во временной области, так и в области подполос. В частности, способы и системы, описываемые в настоящем документе, можно использовать для реализации предсказания подполос непосредственно в области подполос без необходимости в определении и применении предсказателя (например, долгосрочной задержки) во временной области.
Использование в предсказателях подполос межполосных членов позволяет значительно улучшить свойства ограничения шума в частотной области по сравнению с внутриполосными предсказателями (которые полагаются исключительно на внутриполосное предсказание). Действуя таким образом, можно уменьшить артефакты паразитных частот, посредством этого делая возможным использование предсказания подполос для систем кодирования звука с относительно низкими битовыми скоростями передачи данных.
В соответствии с одной из особенностей, описывается способ оценки первого дискретного значения первой подполосы звукового сигнала. Эта первая подполоса звукового сигнала могла быть определена с применением набора анализирующих фильтров, содержащего ряд анализирующих фильтров, создающих из звукового сигнала ряд сигналов подполос, соответственно, в ряду подполос. Звуковой сигнал во временной области может быть передан в набор анализирующих фильтров, приводя к ряду сигналов подполос в ряде подполос. Каждая подполоса из ряда подполос, как правило, охватывает отличающийся диапазон частот звукового сигнала, посредством этого обеспечивая доступ к разным частотным составляющим звукового сигнала. Ряд подполос может иметь равный или равномерный интервал между подполосами. Первая подполоса соответствует одной подполосе из ряда подполос, созданных набором анализирующих фильтров.
Набор анализирующих фильтров может обладать разнообразными свойствами. Набор синтезирующих фильтров, содержащий ряд синтезирующих фильтров, может иметь похожие или такие же свойства. Свойства, описываемые для набора анализирующих фильтров и для анализирующих фильтров, также применимы к свойствам набора синтезирующих фильтров и к синтезирующим фильтрам. Как правило, сочетание набора анализирующих фильтров и набора синтезирующих фильтров делает возможной совершенную реконструкцию звукового сигнала. Анализирующие фильтры из набора анализирующих фильтров могут быть инвариантны относительно сдвига друг относительно друга. В качестве альтернативы или в дополнение, анализирующие фильтры из набора анализирующих фильтров могут содержать общую оконную функцию. В частности, анализирующие фильтры из набора анализирующих фильтров могут содержать по-разному модулированные версии общей оконной функции. В одном из вариантов осуществления общая оконная функция является модулированной с применением косинусной функции, посредством этого приводя к набору косинусно-модулированных анализирующих фильтров. В частности, набор анализирующих фильтров может содержать одно или несколько (или может соответствовать одному или нескольким) из следующих преобразований: MDCT, QMF и/или ELT. Общая оконная функция может иметь конечную длительность К. Длительность общей оконной функции может быть такой, чтобы последовательные дискретные значения сигнала подполосы определялись с применением перекрывающихся сегментов звукового сигнала во временной области. Как таковой, набор анализирующих фильтров может содержать преобразование с перекрытием. Анализирующие фильтры из набора анализирующих фильтров могут образовывать ортогональный и/или ортонормированный базис. В качестве одного из дополнительных свойств набор анализирующих фильтров может соответствовать набору фильтров с критической дискретизацией. В частности, количество дискретных значений из ряда сигналов подполос может соответствовать количеству дискретных значений звукового сигнала во временной области.
Способ может включать определение параметра модели для модели сигнала. Следует отметить, что модель сигнала может быть описана с применением ряда параметров модели. Как таковой, указанный способ может включать определение этого ряда параметров модели для модели сигнала. Параметр (параметры) модели можно извлекать из принятого битового потока, содержащего или служащего признаком параметра модели и сигнала ошибки предсказания. В качестве альтернативы, параметр (параметры) модели можно определять, подбирая модель сигнала для звукового сигнала (например, на покадровой основе), например, с применением подхода среднеквадратичной ошибки.
Модель сигнала может содержать одну или несколько синусоидальных составляющих модели. В этом случае, параметр модели может служить признаком одной или нескольких частот одной или нескольких синусоидальных составляющих модели. В качестве примера, параметр модели может служить признаком основной частоты Ω модели мультисинусоидального сигнала, при этом мультисинусоидальный сигнал содержит синусоидальные составляющие модели на частотах, соответствующих кратным частотам qΩ основной частоты Ω. Как таковая, модель мультисинусоидального сигнала может содержать периодическую составляющую сигнала, при этом периодическая составляющая сигнала содержит ряд синусоидальных составляющих и при этом ряд синусоидальных составляющих имеет частоту, являющуюся кратной основной частоте Ω. Как будет показано в настоящем документе, такую периодическую составляющую сигнала можно использовать для моделирования задержки во временной области (например, используемой в долгосрочных предсказателях). Модель сигнала может содержать один или несколько параметров модели, служащих признаками сдвига и/или отклонения модели сигнала от периодической модели сигнала. Сдвиг и/или отклонение могут служить признаком отклонения частот ряда синусоидальных составляющих периодической модели сигнала от соответствующих кратных частот qΩ основной частоты Ω.
Модель сигнала может содержать ряд периодических составляющих сигнала. Каждая из периодических составляющих сигнала может быть описана с применением одного или нескольких параметров модели. Параметры модели могут служить признаками ряда основных частот 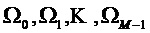 из ряда периодических составляющих сигнала. В качестве альтернативы или в дополнение, модель сигнала можно описать предварительно определяемым и/или корректируемым параметром ослабления (который может представлять собой один из параметров модели). Параметр ослабления может быть рассчитан на выравнивание или сглаживание линейчатого спектра периодической составляющей сигнала. Конкретные примеры моделей сигнала и связанных с ними параметров описываются в разделе вариантов осуществления настоящего документа.
из ряда периодических составляющих сигнала. В качестве альтернативы или в дополнение, модель сигнала можно описать предварительно определяемым и/или корректируемым параметром ослабления (который может представлять собой один из параметров модели). Параметр ослабления может быть рассчитан на выравнивание или сглаживание линейчатого спектра периодической составляющей сигнала. Конкретные примеры моделей сигнала и связанных с ними параметров описываются в разделе вариантов осуществления настоящего документа.
Параметр (параметры) модели можно определить так, чтобы уменьшать (например, минимизировать) среднее значение сигнала квадратичной ошибки предсказания. Сигнал ошибки предсказания можно определить на основе разности между первым дискретным значением и оценкой первого дискретного значения. В частности, среднее значение сигнала квадратичной ошибки предсказания можно определить на основе ряда последовательных первых дискретных значений сигнала первой подполосы и на основе соответствующего ряда оценочных первых дискретных значений. В частности, в настоящем документе предлагается моделировать звуковой сигнал или по меньшей мере сигнал первой подполосы звукового сигнала с применением модели сигнала, описываемой одним или несколькими параметрами модели. Параметры модели используют для определения одного или нескольких коэффициентов предсказания линейного предсказателя, определяющего первый оценочный сигнал подполосы. Разность между сигналом первой подполосы и оценочным сигналом первой подполосы приводит к сигналу подполосы ошибки предсказания. Один или несколько параметров модели можно определить так, чтобы уменьшать (например, минимизировать) среднее значение сигнала подполос квадратичной ошибки предсказания.
Способ может также включать определение коэффициента предсказания, подлежащего применению к предыдущему дискретному значению декодированного сигнала первой подполосы, полученного из сигнала первой подполосы. В частности, предыдущее дискретное значение можно определить путем сложения (квантованной версии) сигнала ошибки предсказания с соответствующим дискретным значением сигнала первой подполосы. Декодированный сигнал первой подполосы может быть идентичен сигналу первой подполосы (например, в случае кодера без потерь). Временной интервал предыдущего дискретного значения, как правило, находится перед временным интервалом первого дискретного значения. В частности, этот способ может включать определение одного или нескольких коэффициентов предсказания рекурсивного фильтра с предсказанием (с конечной импульсной характеристикой), выполненного с возможностью определения первого дискретного значения сигнала первой подполосы исходя из одного или нескольких предыдущих дискретных значений.
Один или несколько коэффициентов предсказания можно определить на основе модели сигнала, на основе параметра модели и на основе набора анализирующих фильтров. В частности, коэффициент предсказания можно определить на основе аналитической оценки модели сигнала и набора анализирующих фильтров. Аналитическая оценка модели сигнала и набора анализирующих фильтров может приводить к определению справочной таблицы и/или аналитической функции. Как таковой, коэффициент предсказания можно определить, используя справочную таблицу и/или аналитическую функцию, при этом справочную таблицу и/или аналитическую функцию можно предварительно определить на основе модели сигнала и на основе набора анализирующих фильтров. Справочная таблица и/или аналитическая функция могут предусматривать коэффициент (коэффициенты) предсказания в зависимости от параметра, полученного исходя из параметра (параметров) модели. Параметр, полученный исходя из параметра модели, может, например, представлять собой параметр модели, или его можно получить исходя из параметра модели с применением предварительно определенной функции. Как таковой, один или несколько коэффициентов предсказания можно определить вычислительно эффективно, используя предварительно определенную справочную таблицу и/или аналитическую функцию, предусматривающую один или несколько коэффициентов предсказания в зависимости (только) от одного или нескольких параметров, полученных (только) исходя из одного или нескольких параметров модели. Таким образом, определение коэффициента предсказания можно свести к простому поиску элемента в справочной таблице.
Как было указано выше, набор анализирующих фильтров может содержать или может проявлять модулированную структуру. Как результат такой модулированной структуры наблюдается, что абсолютное значение одного или нескольких коэффициентов предсказания не зависит от порядкового номера первой подполосы. Это означает, что справочная таблица и/или аналитическая функция может быть инвариантна относительно сдвига (без учета знака) в отношении порядкового номера ряда подполос. В таких случаях параметр, полученный исходя из параметра модели, т.е. параметра, введенного в справочную таблицу и/или аналитическую функцию с целью определения коэффициента предсказания, можно получить, выражая параметр модели относительным образом — в отношении подполосы из ряда подполос.
Как было описано выше, параметр модели может служить признаком основной частоты модели мультисинусоидального сигнала (например, периодической модели сигнала). В таких случаях определение коэффициента предсказания может включать определение кратной частоты основной частоты Ω, лежащей в пределах первой подполосы. Если кратная частота основной частоты Ω лежит в пределах первой подполосы, то можно определить относительное смещение кратной частоты основной частоты Ω от центральной частоты первой подполосы. В частности, можно определить относительное смещение этой кратной частоты основной частоты Ω, ближайшей к центральной частоте первой подполосы. Справочную таблицу и/или аналитическую функцию можно определить так, чтобы справочная таблица и/или аналитическая функция предусматривала коэффициент предсказания в зависимости от возможных относительных смещений от центральной частоты подполосы (например, в зависимости от нормированной частоты 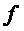 и/или в зависимости от параметра
и/или в зависимости от параметра 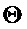 сдвига, описываемого в настоящем документе). Как таковой, коэффициент предсказания можно определить на основе справочной таблицы и/или на основе аналитической функции, используя определенное относительное смещение. Предварительно определенная справочная таблица может включать ограниченное количество элементов для ограниченного количества возможных относительных смещений. В этом случае перед поиском коэффициента предсказания по справочной таблице определяемое относительное смещение можно округлить до ближайшего возможного относительного смещения из ограниченного числа возможных относительных смещений.
сдвига, описываемого в настоящем документе). Как таковой, коэффициент предсказания можно определить на основе справочной таблицы и/или на основе аналитической функции, используя определенное относительное смещение. Предварительно определенная справочная таблица может включать ограниченное количество элементов для ограниченного количества возможных относительных смещений. В этом случае перед поиском коэффициента предсказания по справочной таблице определяемое относительное смещение можно округлить до ближайшего возможного относительного смещения из ограниченного числа возможных относительных смещений.
С другой стороны, если в пределах первой подполосы, точнее, в пределах расширенного диапазона частот, окружающего первую подполосу, не лежит кратная частота основной частоты Ω, коэффициент предсказания может быть приравнен нулю. В этих случаях оценка первого дискретного значения также будет нулевой.
Определение коэффициента предсказания может включать выбор одной из нескольких справочных таблиц на основе параметра модели. Например, параметр модели может служить признаком основной частоты Ω периодической модели сигнала. Основная частота Ω периодической модели сигнала соответствует периодичности T периодической модели сигнала. В настоящем документе показано, что в случае относительно небольших периодичностей T периодическая модель сигнала стремится к односинусоидальной модели. Кроме того, в настоящем документе показано, что в случае относительно больших периодичностей Т справочные таблицы медленно изменяются с абсолютным значением Т и главным образом зависят от относительного смещения (т.е. от параметра 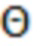 сдвига). Как таковой, ряд справочных таблиц можно предварительно определить для ряда различных значений периодичности Т. Параметр модели (т.е. периодичность Т) можно использовать для выбора подходящей справочной таблицы из ряда справочных таблиц, а коэффициент предсказания можно определить на основе выбранной справочной таблицы из ряда справочных таблиц (используя относительное смещение, например используя параметр
сдвига). Как таковой, ряд справочных таблиц можно предварительно определить для ряда различных значений периодичности Т. Параметр модели (т.е. периодичность Т) можно использовать для выбора подходящей справочной таблицы из ряда справочных таблиц, а коэффициент предсказания можно определить на основе выбранной справочной таблицы из ряда справочных таблиц (используя относительное смещение, например используя параметр 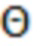 сдвига). Как таковой, параметр модели (представляющий, например, периодичность Т), который может иметь относительно высокую точность, можно с пониженной точностью декодировать в пару параметров (например, в периодичность Т и относительное смещение). Первый параметр (например, периодичность Т) из этой пары параметров можно использовать для выбора конкретной справочной таблицы, а второй параметр (например, относительное смещение) можно использовать для идентификации элемента в выбранной справочной таблице.
сдвига). Как таковой, параметр модели (представляющий, например, периодичность Т), который может иметь относительно высокую точность, можно с пониженной точностью декодировать в пару параметров (например, в периодичность Т и относительное смещение). Первый параметр (например, периодичность Т) из этой пары параметров можно использовать для выбора конкретной справочной таблицы, а второй параметр (например, относительное смещение) можно использовать для идентификации элемента в выбранной справочной таблице.
Способ может также включать определение оценки первого дискретного значения путем применения коэффициента предсказания к предыдущему дискретному значению. Применение коэффициента предсказания к предыдущему дискретному значению может включать умножение коэффициента предсказания на значение предыдущего дискретного значения, посредством чего получается оценка первого дискретного значения. Как правило, применяя коэффициент предсказания к последовательности предыдущих дискретных значений, определяют ряд первых дискретных значений из сигнала первой подполосы. Определение оценки первого дискретного значения также может включать применение масштабного коэффициента передачи к коэффициенту предсказания и/или к первому дискретному значению. Масштабный коэффициент передачи (или его указатель) можно использовать, например, для долгосрочного предсказания (LTP). Иными словами, масштабный коэффициент передачи может вытекать из другого предсказателя (например, из долгосрочного предсказателя). Масштабный коэффициент передачи может отличаться для разных подполос. Кроме того, масштабный коэффициент передачи может передаваться как часть кодированного звукового сигнала.
Как таковое, эффективное описание предсказателя подполос (содержащего один или несколько коэффициентов предсказания) создают, используя модель сигнала, описываемую параметром модели. Параметр модели используют для определения одного или нескольких коэффициентов предсказания для предсказателя подполос. Это означает, что аудиокодер не нуждается в передаче указателя одного или нескольких коэффициентов предсказания, но лишь указателя параметра модели. Как правило, параметр модели можно кодировать более эффективно (т.е. меньшим количеством битов), чем один или несколько коэффициентов предсказания. Поэтому использование предсказания на основе модели делает возможным кодирование подполос с низкой битовой скоростью передачи данных.
Способ может также включать определение маски предсказания, служащей признаком ряда предыдущих дискретных значений в ряду подполос несущего множества маски предсказания. Ряд подполос несущего множества маски предсказания может содержать по меньшей мере одну подполосу из ряда подполос, отличающуюся от первой подполосы. Как таковой, предсказатель подполос может быть выполнен с возможностью оценки дискретного значения из сигнала первой подполосы исходя из дискретных значений одного или нескольких других сигналов подполос из ряда сигналов подполос, отличающихся от сигнала первой подполосы. Это именуется в настоящем документе межполосным предсказанием подполос. Маска предсказания может определять упорядочение ряда предыдущих дискретных значений (например, временное запаздывание относительно временного интервала первой подполосы и/или запаздывание индекса подполосы относительно порядкового номера первой подполосы), используемых для оценки первого дискретного значения из сигнала первой подполосы.
Способ может продолжаться определением ряда коэффициентов предсказания, подлежащих применению к ряду предыдущих дискретных значений. Ряд коэффициентов предсказания можно определить на основе модели сигнала, на основе параметра модели и на основе набора анализирующих фильтров (например, с применением схем предсказания на основе модели, описанных выше в настоящем документе). Как таковой, ряд коэффициентов предсказания можно определить, используя один или несколько параметров модели. Иными словами, для определения ряда коэффициентов предсказания может быть достаточно ограниченного количества параметров модели. Это означает, что посредством использования предсказания подполос на основе модели можно эффективным с точки зрения битовой скорости передачи данных образом реализовать межполосное предсказание подполос.
Способ может включать определение оценки первого дискретного значения путем применения ряда коэффициентов предсказания, соответственно, к ряду предыдущих дискретных значений. Определение оценки первого дискретного значения, как правило, включает определение суммы ряда предыдущих дискретных значений, взвешенной по ряду соответствующих коэффициентов предсказания.
Как было описано выше, параметр модели может служить признаком периодичности Т. Ряд справочных таблиц, используемых для определения одного или нескольких коэффициентов предсказания, может содержать справочные таблицы для разных значений периодичности Т. В частности, ряд справочных таблиц может содержать справочные таблицы для разных значений периодичности Т в пределах интервала [Tmin, Tmax] с предварительно определенным размером шага ∆T. Как будет описано в настоящем документе, Tmin может находиться в интервале 0,25, а Tmax может находиться в интервале 2,5. Tmin можно выбрать так, чтобы при T<Tmin звуковой сигнал мог моделироваться с применением модели сигнала, содержащей односинусоидальную составляющую модели. Tmax можно выбрать так, чтобы при T>Tmax справочные таблицы для периодичностей от Tmax до Tmax+1 по существу соответствовали справочным таблицам для периодичностей от Tmax-1 до Tmax. То же в целом применимо для периодичностей Tmax+n до Tmax+n+1 при 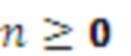 .
.
Способ может включать определение выбранной справочной таблицы в качестве справочной таблицы для периодичности Т, указанной параметром модели. После того как был сделан выбор справочной таблицы, содержащей или указывающей один или несколько коэффициентов предсказания, для идентификации в выбранной справочной таблице подходящего одного или нескольких элементов, указывающих соответственно один или несколько коэффициентов предсказания, можно использовать параметр поиска. Параметр поиска может соответствовать или может быть получен исходя из параметра 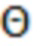 сдвига.
сдвига.
Способ может включать, для параметра модели, служащего признаком периодичности T>Tmax, определение остаточной периодичности Tr путем вычитания целочисленного значения из Т так, чтобы остаточная периодичность Tr лежала в интервале [Tmax-1, Tmax]. Тогда справочную таблицу для определения коэффициента предсказания можно определить как справочную таблицу для остаточной периодичности Tr.
Способ может включать, для параметра модели, служащего признаком периодичности T<Tmin, выбор справочной таблицы для определения одного или нескольких коэффициентов предсказания в качестве справочной таблицы для периодичности Tmin. Кроме того, параметр поиска (например, параметр 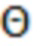 сдвига) для идентификации одного или нескольких элементов выбранной справочной таблицы, обеспечивающих один или несколько коэффициентов предсказания, можно масштабировать в соответствии с отношением
сдвига) для идентификации одного или нескольких элементов выбранной справочной таблицы, обеспечивающих один или несколько коэффициентов предсказания, можно масштабировать в соответствии с отношением 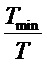 . Тогда один или несколько коэффициентов предсказания можно определить, используя выбранную справочную таблицу и масштабированный параметр поиска. В частности, один или несколько коэффициентов предсказания можно определить на основе одного или нескольких элементов выбранной справочной таблицы, соответствующих масштабированному параметру поиска.
. Тогда один или несколько коэффициентов предсказания можно определить, используя выбранную справочную таблицу и масштабированный параметр поиска. В частности, один или несколько коэффициентов предсказания можно определить на основе одного или нескольких элементов выбранной справочной таблицы, соответствующих масштабированному параметру поиска.
Как таковое, количество справочных таблиц может быть ограничено предварительно определенным интервалом [Tmin, Tmax], посредством чего ограничиваются требования к памяти аудиокодера/аудиодекодера. Тем не менее коэффициенты предсказания можно определить для всех возможных значений периодичности Т, используя предварительно определенные справочные таблицы, посредством этого делая возможным эффективную с вычислительной точки зрения реализацию аудиокодера/аудиодекодера.
В соответствии с одной из дальнейших особенностей описывается способ оценки первого дискретного значения из сигнала первой подполосы звукового сигнала. Как было описано выше, сигнал первой подполосы звукового сигнала можно определить, используя набор анализирующих фильтров, содержащий ряд анализирующих фильтров, создающих соответственно из звукового сигнала ряд сигналов подполос в ряду подполос. Вышеописанные характерные признаки также применимы и к описываемому ниже способу.
Способ включает определение маски предсказания, служащего признаком ряда предыдущих дискретных значений в ряду подполос несущего множества маски предсказания. Ряд подполос несущего множества маски предсказания содержит по меньшей мере одну подполосу из ряда подполос, отличающуюся от первой подполосы. В частности, ряд подполос несущего множества маски предсказания может содержать первую подполосу и/или ряд подполос несущего множества маски предсказания может содержать одну или несколько подполос, непосредственно примыкающих к первой подполосе.
Способ также может включать определение ряда коэффициентов предсказания, подлежащих применению к ряду предыдущих дискретных значений. Ряд предыдущих дискретных значений, как правило, получают исходя из ряда сигналов подполос звукового сигнала. В частности, ряд предыдущих дискретных значений, как правило, соответствует дискретным значениям из ряда декодированных сигналов подполос. Ряд коэффициентов предсказания может соответствовать коэффициентам предсказания из рекурсивного фильтра с предсказанием (с конечной импульсной характеристикой), который также учитывает одно или несколько дискретных значений подполос, отличающихся от первой подполосы. Оценку первого дискретного значения можно определить путем применения ряда коэффициентов предсказания, соответственно, к ряду предыдущих дискретных значений. Как таковой, способ делает возможным предсказание подполосы с применением одного или нескольких дискретных значений из других (например, смежных) подполос. Действуя таким образом, можно уменьшить артефакты паразитных частот, вызываемые кодерами на основе предсказания подполос.
Способ может также включать определение параметра модели для модели сигнала. Ряд коэффициентов предсказания можно определить на основе модели сигнала, основанной на параметре модели, и на основе набора анализирующих фильтров. Как таковой, ряд коэффициентов предсказания можно определить с применением предсказания на основе модели, описываемого в настоящем документе. В частности, ряд коэффициентов предсказания можно определить с применением справочной таблицы и/или аналитической функции. Справочную таблицу и/или аналитическую функцию можно предварительно определить на основе модели сигнала и на основе набора анализирующих фильтров. Кроме того, справочная таблица и/или аналитическая функция может предусматривать ряд коэффициентов предсказания (только) в зависимости от параметра, полученного исходя из параметра модели. Таким образом, параметр модели может непосредственно предусматривать ряд коэффициентов предсказания при использовании справочной таблицы и/или аналитической функции. Как таковой, этот параметр модели можно использовать для эффективного описания коэффициента межполосного предсказателя.
В соответствии с одной из дальнейших особенностей изобретения описывается способ кодирования звукового сигнала. Способ может включать определение ряда сигналов подполос исходя из звукового сигнала с применением набора анализирующих фильтров, содержащего ряд анализирующих фильтров. Способ можно продолжить оценкой дискретных значений ряда сигналов подполос с применением любого из способов предсказания, описываемых в настоящем документе, посредством чего получается ряд оценочных сигналов подполос. Кроме того, на основе соответствующих дискретных значений из ряда сигналов подполос и дискретных значений из ряда оценочных сигналов подполос можно определить дискретные значения из ряда сигналов подполос ошибок предсказания. Способ можно продолжить квантованием ряда сигналов подполос ошибок предсказания и генерированием кодированного звукового сигнала. Этот кодированный звуковой сигнал может служить признаком (например, может содержать) ряда квантованных сигналов подполос ошибок предсказания. Кроме того, кодированный сигнал может служить признаком (например, может содержать) одного или несколько параметров, использованных для оценки дискретных значений из ряда оценочных сигналов подполос, например, служащих признаком одного или нескольких параметров модели, использованных при определении одного или нескольких коэффициентов предсказания, которые затем были использованы для оценки дискретных значений из ряда оценочных сигналов подполос.
В соответствии с другой особенностью описывается способ декодирования кодированного звукового сигнала. Кодированный звуковой сигнал, как правило, служит признаком ряда квантованных сигналов подполос ошибок предсказания и одного или нескольких параметров, подлежащих использованию при оценке дискретных значений из ряда оценочных сигналов подполос. Способ может включать деквантование ряда квантованных сигналов подполос ошибок предсказания, посредством чего получается ряд деквантованных сигналов подполос ошибок предсказания. Кроме того, способ может включать оценку дискретных значений из ряда оценочных сигналов подполос с применением любого из способов предсказания, описываемых в настоящем документе. Дискретные значения из ряда декодированных сигналов подполос можно определить на основе соответствующих дискретных значений из ряда оценочных сигналов подполос и на основе дискретных значений из ряда деквантованных сигналов подполос ошибок предсказания. Декодированный звуковой сигнал можно определить исходя из ряда декодированных сигналов подполос с применением набора синтезирующих фильтров, содержащего ряд синтезирующих фильтров.
В соответствии с одной из дальнейших особенностей описывается система, выполненная с возможностью оценки одного или нескольких первых дискретных значений из сигнала первой подполосы звукового сигнала. Сигнал первой подполосы звукового сигнала можно определить, используя набор анализирующих фильтров, содержащий ряд анализирующих фильтров, создающих ряд сигналов подполос исходя из звукового сигнала в ряду соответствующих подполос. Система может содержать вычислитель предсказателя, выполненный с возможностью определения параметра модели для модели сигнала. Кроме того, вычислитель предсказателя может быть выполнен с возможностью определения одного или нескольких коэффициентов предсказания, подлежащих применению к одному или нескольким предыдущим дискретным значениям декодированного сигнала первой подполосы. Как таковой, вычислитель предсказателя может быть выполнен с возможностью определения одного или нескольких коэффициентов предсказания из рекурсивного фильтра с предсказанием, в частности рекурсивного фильтра с предсказанием подполос. Один или несколько коэффициентов предсказания можно определить на основе модели сигнала, основанной на параметре модели, и на основе набора анализирующих фильтров (например, используя способы предсказания на основе модели, описываемые в настоящем документе). Временные интервалы одного или нескольких предыдущих дискретных значений находятся, как правило, перед временными интервалами одного или нескольких первых дискретных значений. Система также может содержать предсказатель подполос, выполненный с возможностью определения оценки одного или нескольких первых дискретных значений путем применения одного или нескольких коэффициентов предсказания к одному или нескольким предыдущим дискретным значениям.
В соответствии с другой особенностью описывается система, выполненная с возможностью оценки одного или нескольких первых дискретных значений из сигнала первой подполосы звукового сигнала. Этот сигнал первой подполосы соответствует первой подполосе из ряда подполос. Сигнал первой подполосы, как правило, определяют, используя набор анализирующих фильтров, содержащий ряд анализирующих фильтров, создающих ряд сигналов подполос, соответственно, для ряда подполос. Система содержит вычислитель предсказателя, выполненный с возможностью определения маски предсказания, служащей признаком ряда предыдущих дискретных значений в ряду подполос несущего множества маски предсказания. Ряд подполос несущего множества маски предсказания содержит по меньшей мере одну подполосу из ряда подполос, отличающуюся от первой подполосы. Вычислитель предсказателя также выполнен с возможностью определения ряда коэффициентов предсказания (или рекурсивного фильтра с предсказанием), подлежащих применению к ряду предыдущих дискретных значений. Кроме того, система содержит предсказатель подполос, выполненный с возможностью определения оценки одного или нескольких первых дискретных значений путем применения ряда коэффициентов предсказания, соответственно, к ряду предыдущих дискретных значений.
В соответствии с другой особенностью описывается аудиокодер для кодирования звукового сигнала. Аудиокодер содержит набор анализирующих фильтров, выполненный с возможностью определения ряда сигналов подполос исходя из звукового сигнала с применением ряда анализирующих фильтров. Кроме того, аудиокодер содержит вычислитель предсказателя и предсказатель подполос, описываемые в настоящем документе, выполненные с возможностью оценки дискретных значений ряда сигналов подполос, посредством чего получается ряд оценочных сигналов подполос. Кроме того, кодер может содержать разностный модуль, выполненный с возможностью определения дискретных значений из ряда сигналов подполос ошибок предсказания на основе соответствующих дискретных значений из ряда сигналов подполос и ряда оценочных сигналов подполос. Для квантования ряда сигналов подполос ошибок предсказания можно использовать модуль квантования. Кроме того, модуль генерирования битового потока может быть выполнен с возможностью генерирования кодированного звукового сигнала, служащего признаком ряда квантованных сигналов подполос ошибок предсказания и одного или нескольких параметров (например, одного или нескольких параметров модели), используемых при оценке дискретных значений из ряда оценочных сигналов подполос.
В соответствии с одной из дальнейших особенностей описывается аудиодекодер, выполненный с возможностью декодирования кодированного звукового сигнала. Кодированный звуковой сигнал служит признаком (например, содержит) ряда квантованных сигналов подполос ошибок предсказания и одного или нескольких параметров, использованных при оценке дискретных значений из ряда оценочных сигналов подполос. Аудиодекодер может содержать обратный квантователь, выполненный с возможностью деквантования ряда квантованных сигналов подполос ошибок предсказания, посредством чего получается ряд деквантованных сигналов подполос ошибок предсказания. Кроме того, декодер содержит вычислитель предсказателя и предсказатель подполос, описываемые в настоящем документе, выполненные с возможностью оценки дискретных значений из ряда оценочных сигналов подполос. Для определения дискретных значений ряда декодированных сигналов подполос на основе соответствующих дискретных значений из ряда оценочных сигналов подполос и на основе дискретных значений из ряда деквантованных сигналов подполос ошибок предсказания можно использовать суммирующий модуль. Кроме того, для определения декодированного звукового сигнала исходя из ряда декодированных сигналов подполос с применением ряда синтезирующих фильтров можно использовать набор синтезирующих фильтров.
В соответствии с одной из дальнейших особенностей описывается программа, реализованная программно. Программа, реализованная программно, может быть приспособлена для исполнения на процессоре и для выполнения этапов способов, описываемых в настоящем документе, при осуществлении на процессоре.
В соответствии с другой особенностью описывается носитель данных. Носитель данных может содержать программу, реализованную программно и приспособленную для исполнения на процессоре и для выполнения этапов способов, описываемых в настоящем документе, при осуществлении на процессоре.
В соответствии с одной из дальнейших особенностей описывается компьютерный программный продукт. Компьютерный программный продукт может содержать исполняемые команды для выполнения этапов способов, описываемых в настоящем документе, при исполнении на компьютере.
Следует отметить, что способы и системы, включая их предпочтительные варианты осуществления, описываемые в этой патентной заявке, можно использовать автономно или в сочетании с другими способами и системами, описываемыми в настоящем документе. Кроме того, все особенности способов и систем, описываемых в этой патентной заявке, можно произвольно сочетать. В частности, произвольно можно сочетать друг с другом характерные признаки, изложенные в формуле изобретения.
КРАТКОЕ ОПИСАНИЕ ГРАФИЧЕСКИХ МАТЕРИАЛОВ
Настоящее изобретение описывается ниже на иллюстративных примерах, не ограничивающих объем или суть изобретения, со ссылкой на сопроводительные графические материалы, в которых:
фиг. 1 изображает блок-схему одного из примеров аудиодекодера, применяющего линейное предсказание в области набора фильтров (т.е. в области подполос);
фиг. 2 показывает пример масок предсказания в частотно-временной сетке;
фиг. 3 иллюстрирует пример табличных данных для вычислителя предсказателя на основе синусоидальной модели;
фиг. 4 иллюстрирует пример ограничения шума в результате внутриполосного предсказания подполос;
фиг. 5 иллюстрирует пример ограничения шума в результате межполосного предсказания подполос; и
фиг. 6a изображает один из примеров двумерной сетки квантования, лежащей в основе табличных данных для вычисления предсказателя на основе периодической модели;
фиг. 6b иллюстрирует использование разных масок предсказания для разных интервалов периодичностей сигнала; и
фиг. 7a и 7b показывают схемы последовательностей иллюстративных способов кодирования и декодирования с применением предсказания подполос на основе модели.
ПОДРОБНОЕ ОПИСАНИЕ
Описываемые ниже варианты осуществления являются лишь иллюстрирующими принципы настоящего изобретения для предсказания на основе модели в наборе фильтров с критической дискретизацией. Следует понимать, что специалистам в данной области техники будут очевидны модификации и изменения схем и подробностей, описываемых в настоящем документе. Поэтому намерение заключается в ограничении только объемом предстоящей формулы изобретения, а не конкретными подробностями, представленными в настоящем документе с целью описания и разъяснения вариантов осуществления.
Фиг. 1 изображает блок-схему одного из примеров аудиодекодера 100, применяющего линейное предсказание в области набора фильтров (также именуемой областью подполос). Аудиодекодер 100 принимает битовый поток, содержащий информацию в отношении сигнала ошибки предсказания (также именуемого остаточным сигналом) и, возможно, информацию в отношении описания предсказателя, использованного соответствующим кодером для определения сигнала ошибки предсказания исходя из исходного входного звукового сигнала. Информация в отношении сигнала ошибки предсказания может относиться к подполосам входного звукового сигнала, а информация в отношении описания предсказателя может относиться к одному или нескольким предсказателям подполос.
Для данной полученной информации битового потока обратный квантователь 101 может выводить дискретные значения 111 сигналов подполос ошибок предсказания. Эти дискретные значения могут быть добавлены к выводу 112 предсказателя 103 подполос, а сумма 113 может проходить в буфер 104 подполос, ведущий учет предыдущих декодированных дискретных значений 113 подполос декодированного звукового сигнала. Вывод предсказателя 103 подполос можно именовать оценочными сигналами 112 подполос. Декодированные дискретные значения 113 подполос декодированного звукового сигнала могут подаваться в набор 102 синтезирующих фильтров, преобразующий дискретные значения подполос во временную область, посредством этого приводя к дискретным значениям 114 временной области декодированного звукового сигнала.
Иными словами, декодер 100 может действовать в области подполос. В частности, декодер 100 может определять ряд оценочных сигналов 112 подполос, используя предсказатель 103 подполос. Кроме того, декодер 100 может определять ряд остаточных сигналов 111 подполос, используя обратный квантователь 101. Соответствующие пары из ряда оценочных сигналов 112 подполос и ряда остаточных сигналов 111 подполос можно складывать, получая соответствующий ряд декодированных сигналов 113 подполос. Этот ряд декодированных сигналов 113 подполос может подаваться в набор 102 синтезирующих фильтров, приводящий к декодированному звуковому сигналу 114 во временной области.
В одном из вариантов осуществления предсказателя 103 подполос данное дискретное значение из данного оценочного сигнала 112 подполосы можно получить путем линейной комбинации дискретных значений подполос из буфера 104, соответствующих иному времени и иной частоте (т.е. иной подполосе), отличных от данного дискретного значения из данного оценочного сигнала 112 подполосы. Иными словами, дискретное значение из оценочного сигнала 112 подполосы в первый момент времени и в первой подполосе можно определить на основе одного или нескольких дискретных значений из декодированных сигналов 113 подполос, относящихся ко второму моменту времени (отличному от первого момента времени) и относящихся ко второй подполосе (отличной от первой подполосы). Совокупность коэффициентов предсказания и их прикрепление к временной и частотной маске может определять предсказатель 103, и эту информацию представляет вычислитель 105 предсказателя декодера 100. Вычислитель 105 предсказателя выводит информацию, определяющую предсказатель 103 посредством преобразования данных модели сигнала, заключенных в принятом битовом потоке. Может быть передан дополнительный коэффициент передачи, модифицирующий масштаб вывода предсказателя 103. В одном из вариантов осуществления вычислителя 105 предсказателя данные модели сигнала представлены в форме эффективно параметризованного линейчатого спектра, при этом каждую линию в этом параметризованном линейчатом спектре или группе последовательных линий в параметризованном линейчатом спектре используют для указания табличных значений коэффициентов предсказателя. Как таковые, данные модели сигнала, доставленные в принятом битовом потоке, можно использовать для идентификации элементов в предварительно определенной справочной таблице, при этом элементы из справочной таблицы предусматривают одно или несколько значений коэффициентов предсказателя (также именуемых коэффициентами предсказания), подлежащих использованию предсказателем 103. Способ, применяемый для поиска в таблице, может зависеть от компромиссов между сложностью и требованиями к памяти. Например, для достижения наиболее низкой сложности можно использовать поиск по типу ближайшего соседа, в то время как интерполяционный способ поиска может обеспечивать аналогичную производительность для таблицы меньшего размера.
Как было указано выше, принимаемый битовый поток может содержать один или несколько передаваемых в явном виде коэффициентов передачи (или передаваемых в явном виде указателей коэффициентов передачи). Коэффициенты передачи можно применять как часть операции предсказания или после нее. Один или несколько передаваемых в явном виде коэффициентов передачи могут отличаться для разных подполос. Передаваемые в явном виде (в форме указателей) дополнительные коэффициенты передачи доставляются в дополнение к одному или нескольким параметрам модели, используемым для определения коэффициентов предсказания предсказателя 103. Как таковые, дополнительные коэффициенты передачи можно использовать для масштабирования коэффициентов предсказания предсказателя 103.
Фиг. 2 показывает пример несущих множеств маски предсказания в частотно-временной сетке. Несущие множества маски предсказания можно использовать для предсказателей 103, действующих в наборе фильтров с равномерной частотно-временной разрешающей способностью, таком как набор косинусно-модулированных фильтров (например, набор фильтров MDCT). Обозначение проиллюстрировано схемой 201, в которой целевое дискретное значение 211 подполосы темного оттенка представляет собой вывод предсказания на основе дискретного значения 212 подполосы светлого оттенка. На схемах 202—205 совокупность дискретных значений подполос светлого оттенка указывает несущее множество маски предсказания. Сочетание исходных дискретных значений 212 подполос и целевых дискретных значений 211 подполос будет именоваться маской 201 предсказания. Частотно-временную сетку можно использовать для упорядочения дискретных значений подполос вблизи целевого дискретного значения подполосы. Индекс временных интервалов увеличивается слева направо, а индекс частот подполос увеличивается снизу вверх. Фиг. 2 показывает иллюстративные случаи масок предсказания и несущие множества масок предсказателя, и следует отметить, что можно использовать другие различные маски предсказания и несущие множества масок предсказателя. Примерами масок предсказания являются:
• Маска 202 предсказания определяет внутриполосное предсказание оценочного дискретного значения 221 подполосы в момент времени k исходя из двух предыдущих декодированных дискретных значений 222 подполосы в моменты времени k–1 и k–2.
• Маска 203 предсказания определяет межполосное предсказание оценочного дискретного значения 231 подполосы в момент времени k и в подполосе n на основе трех предыдущих декодированных дискретных значений 232 подполос в момент времени k–1 в подполосах n–1, n, n+1.
• Маска 204 предсказания определяет межполосное предсказание трех оценочных дискретных значений 241 подполос в момент времени k и в трех различных подполосах n–1, n, n+1 на основе трех предыдущих декодированных дискретных значений 242 подполос в момент времени k–1 в подполосах n–1, n, n+1. Межполосное предсказание можно выполнять так, чтобы каждое оценочное дискретное значение 241 подполосы можно было определить на основе всех трех предыдущих декодированных дискретных значений 242 подполос в подполосах n–1, n, n+1.
• Маска 205 предсказания определяет межполосное предсказание оценочного дискретного значения 251 подполосы в момент времени k и в подполосе n на основе двенадцати предыдущих декодированных дискретных значений 252 подполос в моменты времени k–2, k–3, k–4, k–5 и в подполосах n–1, n, n+1.
Фиг. 3 иллюстрирует табличные данные для вычислителя 105 предсказателя на основе синусоидальной модели, предусмотренного в наборе косинусно-модулированных фильтров. Несущее множество маски предсказания является таким же, как на схеме 204. Для данного параметра частоты в качестве центральной целевой подполосы можно выбрать подполосу с ближайшей центральной частотой подполосы. Разность между параметром частоты и центральной частотой центральной целевой подполосы можно вычислить в единицах разноса частот набора фильтров (элементов разрешения). Это дает значение –0,5-0,5, которое можно округлить до ближайшего доступного элемента в табличных данных, изображенных абсциссами на девяти графиках 301 по фиг. 3. Это вырабатывает матрицу размера 3×3 из коэффициентов, подлежащих применению к самым новым значениям из ряда декодированных сигналов 113 подполос в буфере 104 подполос для целевой подполосы и двух смежных с ней подполос. Результирующий вектор размера 3×1 составляет вклад предсказателя 103 подполос в эти три подполосы для данного параметра частоты. Этот процесс можно повторить аддитивным образом для всех синусоидальных составляющих в модели сигнала.
Иными словами, фиг. 3 иллюстрирует один из примеров описания предсказателя подполос на основе модели. Предполагается, что входной звуковой сигнал содержит одну или несколько синусоидальных составляющих с основными частотами 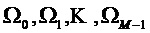 . Для каждой одной или нескольких синусоидальных составляющих можно, используя предварительно определенную маску предсказания (например, маску 204 предсказания), определить предсказатель подполос. Основная частота
. Для каждой одной или нескольких синусоидальных составляющих можно, используя предварительно определенную маску предсказания (например, маску 204 предсказания), определить предсказатель подполос. Основная частота 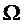 входного звукового сигнала может лежать в пределах одной из подполос набора фильтров. Эта подполоса может именоваться центральной подполосой для этой конкретной основной частоты
входного звукового сигнала может лежать в пределах одной из подполос набора фильтров. Эта подполоса может именоваться центральной подполосой для этой конкретной основной частоты 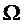 . Основную частоту
. Основную частоту 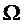 можно выразить как значение в интервале –0,5-0,5 относительно центральной частоты центральной подполосы. Аудиокодер может передавать информацию, касающуюся этой основной частоты
можно выразить как значение в интервале –0,5-0,5 относительно центральной частоты центральной подполосы. Аудиокодер может передавать информацию, касающуюся этой основной частоты 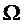 , в декодер 100. Вычислитель 105 предсказателя декодера 100 может использовать матрицу размера три на три по фиг. 3 для определения матрицы три на три из коэффициентов предсказания путем определения значения 302 коэффициента для значения 303 относительной частоты основной частоты
, в декодер 100. Вычислитель 105 предсказателя декодера 100 может использовать матрицу размера три на три по фиг. 3 для определения матрицы три на три из коэффициентов предсказания путем определения значения 302 коэффициента для значения 303 относительной частоты основной частоты 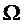 . Это означает, что коэффициент предсказателя 103 подполос, использующего маску 204 предсказания, можно определить, используя только принятую информацию, касающуюся конкретной основной частоты
. Это означает, что коэффициент предсказателя 103 подполос, использующего маску 204 предсказания, можно определить, используя только принятую информацию, касающуюся конкретной основной частоты 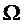 . Иными словами, путем моделирования входного звукового сигнала с применением, например, модели из одной или нескольких синусоидальных составляющих можно создать эффективное с точки зрения битовой скорости передачи данных описание предсказателя подполос.
. Иными словами, путем моделирования входного звукового сигнала с применением, например, модели из одной или нескольких синусоидальных составляющих можно создать эффективное с точки зрения битовой скорости передачи данных описание предсказателя подполос.
Фиг. 4 иллюстрирует пример ограничения шума, являющегося результатом внутриполосного предсказания подполос в наборе косинусно-модулированных фильтров. Модель сигнала, использованная для выполнения внутриполосного предсказания подполос, представляет собой авторегрессивный стохастический процесс второго порядка с островершинным резонансом, описываемый дифференциальным уравнением второго порядка, управляемым случайным гауссовским белым шумом. Кривая 401 показывает измеренный спектр абсолютных значений для одной из реализаций процесса. Для этого примера применяют маску 202 предсказания по фиг. 2. То есть вычислитель 105 предсказателя представляет предсказатель 103 подполос для заданной целевой подполосы 221 на основе только предыдущих дискретных значений 222 в той же подполосе. Замена обратного квантователя 101 генератором гауссовского белого шума приводит к синтезированному спектру 402 абсолютных значений. Как видно, при синтезе возникают сильные артефакты паразитных частот, так как синтезированный спектр 402 содержит пики, не совпадающие с исходным спектром 401.
Фиг. 5 иллюстрирует пример ограничения шума, возникающего в результате межполосного предсказания подполос. Условия являются такими же, как по фиг. 4, за исключением того, что применяется маска 203 предсказания. Поэтому вычислитель 105 представляет предсказатель 103 для заданной целевой подполосы 231 на основе предыдущих дискретных значений 232 подполос в этой целевой подполосе и в двух смежных подполосах. Как видно на фиг. 5, спектр 502 синтезированного сигнала по существу совпадает со спектром 501 исходного сигнала, т.е. при использовании межполосного предсказания подполос проблемы паразитных частот по существу подавляются.
Таким образом, фиг. 4 и 5 иллюстрируют то, что при использовании межполосного предсказания подполос, т.е. при предсказании дискретного значения подполосы на основе предыдущих дискретных значений подполос из одной или нескольких смежных подполос, можно уменьшить артефакты паразитных частот, вызванные предсказанием подполосы. В результате предсказание подполос также можно применить в контексте аудиокодеров с низкой битовой скоростью передачи данных без риска вызова слышных артефактов паразитных частот. Использование межполосного предсказания подполос, как правило, увеличивает количество коэффициентов предсказания. Однако, как показано на фиг. 3, использование моделей входного звукового сигнала (например, использование синусоидальной модели или периодической модели) делает возможным эффективное описание предсказателя подполос, посредством этого позволяя использовать межполосное предсказание подполос для аудиокодеров с низкой битовой скоростью передачи данных.
Ниже со ссылкой на фиг. 1—6 и посредством добавления соответствующей математической терминологии будет дано описание принципов предсказания на основе модели в наборе фильтров с критической дискретизацией.
Возможной моделью сигнала, лежащей в основе линейного предсказания, является модель слабостационарного стохастического процесса 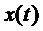 с нулевым средним, статистика которого определяется его автокорреляционной функцией
с нулевым средним, статистика которого определяется его автокорреляционной функцией 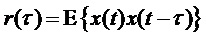 . Для рассмотрения в качестве хорошей модели наборов фильтров с критической дискретизацией пусть
. Для рассмотрения в качестве хорошей модели наборов фильтров с критической дискретизацией пусть 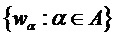 — совокупность вещественнозначных форм синтезируемых сигналов
— совокупность вещественнозначных форм синтезируемых сигналов 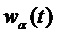 , составляющих ортогональный базис. Иными словами, набор фильтров можно представить формами сигналов
, составляющих ортогональный базис. Иными словами, набор фильтров можно представить формами сигналов 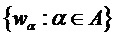 . Дискретные значения подполос сигнала
. Дискретные значения подполос сигнала 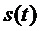 во временной области получаются путем скалярных произведений
во временной области получаются путем скалярных произведений
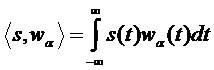 , (1)
, (1)
а сигнал находят как
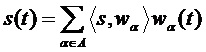 . (2)
. (2)
Дискретные значения подполос 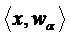 из процесса
из процесса 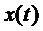 представляют собой случайные переменные, ковариационная матрица Rαβ которых определяется автокорреляционной функцией
представляют собой случайные переменные, ковариационная матрица Rαβ которых определяется автокорреляционной функцией 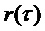 следующим образом:
следующим образом:
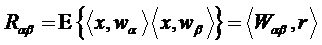 , (3)
, (3)
где 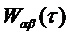 — взаимная корреляция двух форм синтезируемых сигналов:
— взаимная корреляция двух форм синтезируемых сигналов:
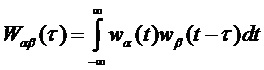 . (4)
. (4)
Линейное предсказание дискретного значения подполосы 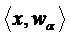 определяется исходя из совокупности декодированных дискретных значений подполос
определяется исходя из совокупности декодированных дискретных значений подполос 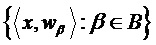 как
как
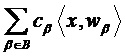 . (5)
. (5)
В уравнении (5) множество 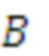 определяет исходные дискретные значения подполос, т.е. множество
определяет исходные дискретные значения подполос, т.е. множество 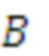 определяет несущее множество маски предсказания. Среднее значение квадратичной ошибки предсказания имеет вид:
определяет несущее множество маски предсказания. Среднее значение квадратичной ошибки предсказания имеет вид:
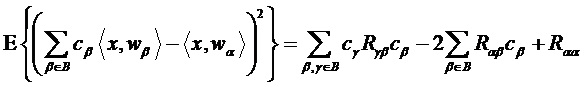 , (6)
, (6)
и решение минимальной среднеквадратичной ошибки (MSE) получают путем решения нормальных уравнений для коэффициентов предсказания 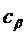 :
:
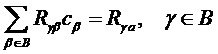 . (7)
. (7)
Если коэффициенты предсказания удовлетворяют уравнению (7), правую сторону уравнения (6) приводят к виду 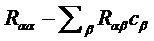 . Нормальные уравнения (7) можно эффективно решать, используя, например, алгоритм Левинсона-Дарбина.
. Нормальные уравнения (7) можно эффективно решать, используя, например, алгоритм Левинсона-Дарбина.
В настоящем документе предлагается передавать параметрическое представление модели сигнала, из которой коэффициенты предсказания 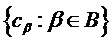 можно получить в вычислителе 105 предсказателя. Например, модель сигнала может предусматривать параметрическое представление автокорреляционной функции
можно получить в вычислителе 105 предсказателя. Например, модель сигнала может предусматривать параметрическое представление автокорреляционной функции 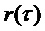 модели сигнала. Декодер 100 может получать автокорреляционную функцию
модели сигнала. Декодер 100 может получать автокорреляционную функцию 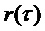 , используя принятое параметрическое представление, и может объединять автокорреляционную функцию
, используя принятое параметрическое представление, и может объединять автокорреляционную функцию 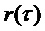 с взаимной корреляцией
с взаимной корреляцией 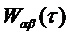 формы синтезируемого сигнала, чтобы получать элементы ковариационной матрицы, требуемые для нормальных уравнений (7). Эти уравнения можно затем решать с целью получения коэффициентов предсказания.
формы синтезируемого сигнала, чтобы получать элементы ковариационной матрицы, требуемые для нормальных уравнений (7). Эти уравнения можно затем решать с целью получения коэффициентов предсказания.
Иными словами, подлежащий кодированию входной звуковой сигнал можно смоделировать процессом 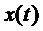 , который можно описать, используя ограниченное количество параметров модели. В частности, модельный процесс
, который можно описать, используя ограниченное количество параметров модели. В частности, модельный процесс 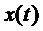 может быть таким, что его автокорреляционную функцию
может быть таким, что его автокорреляционную функцию 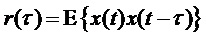 можно описать, используя ограниченное количество параметров. Ограниченное количество параметров для описания автокорреляционной функции
можно описать, используя ограниченное количество параметров. Ограниченное количество параметров для описания автокорреляционной функции 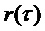 можно передать в декодер 100. Вычислитель 105 предсказателя декодера 100 может определять автокорреляционную функцию
можно передать в декодер 100. Вычислитель 105 предсказателя декодера 100 может определять автокорреляционную функцию 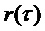 , исходя из принятых параметров, и может использовать уравнение (3) для определения ковариационной матрицы
, исходя из принятых параметров, и может использовать уравнение (3) для определения ковариационной матрицы 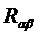 сигналов подполос, из которой можно определить нормальное уравнение (7). Нормальное уравнение (7) может быть затем решено вычислителем 105 предсказателя, посредством чего получаются коэффициенты
сигналов подполос, из которой можно определить нормальное уравнение (7). Нормальное уравнение (7) может быть затем решено вычислителем 105 предсказателя, посредством чего получаются коэффициенты 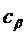 предсказания.
предсказания.
Ниже описаны примеры моделей сигналов, которые можно эффективно использовать для применения вышеописанной схемы предсказания на основе модели. Модели сигналов, описываемые ниже, как правило, являются в высокой степени значимыми для кодирования звуковых сигналов, например для кодирования речевых сигналов.
Один из примеров модели сигнала имеет вид синусоидального процесса:
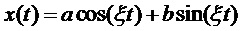 , (8)
, (8)
где случайные переменные 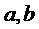 являются некоррелирующими, имеют нулевое среднее и вариантность, равную единице.
являются некоррелирующими, имеют нулевое среднее и вариантность, равную единице.
Автокорреляционная функция этого синусоидального процесса имеет вид:
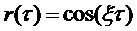 . (9)
. (9)
Обобщение такого синусоидального процесса в мультисинусной модели содержит набор (угловых) частот 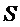 , т.е. содержит ряд различных (угловых) частот
, т.е. содержит ряд различных (угловых) частот 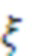 ,
,
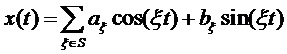 . (10)
. (10)
Полагая, что все случайные переменные 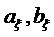 являются попарно некоррелирующими, имеют нулевое среднее и вариантность, равную единице, мультисинусный процесс имеет автокорреляционную функцию:
являются попарно некоррелирующими, имеют нулевое среднее и вариантность, равную единице, мультисинусный процесс имеет автокорреляционную функцию:
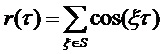 . (11)
. (11)
Спектральная плотность мощности (PSD) мультисинусного процесса (соответствующая преобразованию Фурье автокорреляционной функции) представляет собой линейчатый спектр:
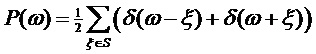 . (12)
. (12)
Численные соображения могут приводить к замене чисто мультисинусного процесса автокорреляционной функцией тождественного процесса с ослабленным мультисинусным процессом, имеющим автокорреляционную функцию 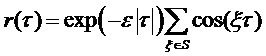 , где
, где 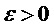 — относительно небольшой параметр ослабления. Последняя модель приводит к строго положительной PSD без импульсных функций.
— относительно небольшой параметр ослабления. Последняя модель приводит к строго положительной PSD без импульсных функций.
Примеры компактных описаний набора из S частот мультисинусной модели являются следующими:
1. Единственная основная частота 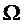 :
: 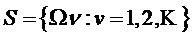
2. М основных частот: Ω0,Ω1,…,ΩМ-1: 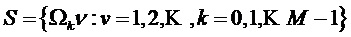
3. Единственная боковая полоса, сдвинутая на основную частоту 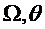 :
: 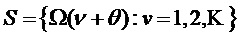
4. Слабо негармоническая модель: 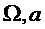 :
: 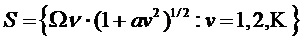 , где
, где 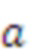 описывает негармоническую составляющую модели.
описывает негармоническую составляющую модели.
Как таковую, мультисинусную модель (возможно, ослабленную), проявляющую PSD, заданную уравнением (12), можно эффективно описать, используя одно из вышеперечисленных иллюстративных описаний. Для примера, полный набор 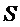 частот в линейчатом спектре по уравнению (12) можно описать, используя только единственную основную частоту Ω. Если подлежащий кодированию входной звуковой сигнал вполне можно описать, используя мультисинусную модель, проявляющую единственную основную частоту
частот в линейчатом спектре по уравнению (12) можно описать, используя только единственную основную частоту Ω. Если подлежащий кодированию входной звуковой сигнал вполне можно описать, используя мультисинусную модель, проявляющую единственную основную частоту 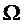 , то предсказатель на основе модели можно описать единственным параметром (например, основной частотой
, то предсказатель на основе модели можно описать единственным параметром (например, основной частотой 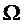 ) независимо от количества коэффициентов предсказания (т.е. независимо от маски 202, 203, 204, 205 предсказания), используемых предсказателем 103 подполос.
) независимо от количества коэффициентов предсказания (т.е. независимо от маски 202, 203, 204, 205 предсказания), используемых предсказателем 103 подполос.
Случай 1 для описания набора 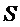 частот приводит к процессу
частот приводит к процессу 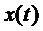 , моделирующему входные звуковые сигналы с периодом
, моделирующему входные звуковые сигналы с периодом 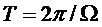 . При включении в уравнение (11) нулевой частоты (DC) с вариантностью ½ и подверганию результата изменению масштаба в
. При включении в уравнение (11) нулевой частоты (DC) с вариантностью ½ и подверганию результата изменению масштаба в 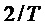 раз, автокорреляционную функцию этой периодической модели можно записать как
раз, автокорреляционную функцию этой периодической модели можно записать как
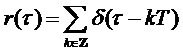 . (13)
. (13)
С учетом определения коэффициента ослабления 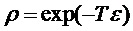 автокорреляционная функция ослабленной версии периодической модели имеет вид:
автокорреляционная функция ослабленной версии периодической модели имеет вид:
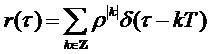 . (14)
. (14)
Уравнение (14) также соответствует автокорреляционной функции процесса, определяемого единственным циклом задержки, снабжаемым белым шумом 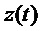 , то есть процесса модели:
, то есть процесса модели:
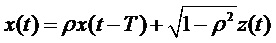 . (15)
. (15)
Это означает, что периодический процесс, проявляющий единственную основную частоту 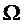 , соответствует задержке во временной области, при этом задержка представляет собой
, соответствует задержке во временной области, при этом задержка представляет собой 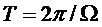 .
.
Вышеупомянутые всеобщие модели сигналов, как правило, имеют плоский спектр мощности в большом масштабе по причине допущения единичной вариантности синусоидальных амплитудных параметров 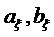 . Однако следует отметить, что модели сигналов, как правило, рассматривают лишь локально для подмножества подполос набора фильтров с критической дискретизацией, причем набор фильтров служит инструментальным средством формирования полного спектра. Иными словами, для сигнала, имеющего форму спектра с малым изменением в сравнении с ширинами подполос, модели плоского спектра мощности будут обеспечивать хорошее согласование с сигналом, и, соответственно, предсказатели на основе модели будут выражать достаточные уровни коэффициента передачи предсказания.
. Однако следует отметить, что модели сигналов, как правило, рассматривают лишь локально для подмножества подполос набора фильтров с критической дискретизацией, причем набор фильтров служит инструментальным средством формирования полного спектра. Иными словами, для сигнала, имеющего форму спектра с малым изменением в сравнении с ширинами подполос, модели плоского спектра мощности будут обеспечивать хорошее согласование с сигналом, и, соответственно, предсказатели на основе модели будут выражать достаточные уровни коэффициента передачи предсказания.
В более общем смысле модель PSD можно было бы описать в выражении стандартных параметризаций авторегрессивного (AR) процесса или процесса авторегрессивного скользящего среднего (ARMA). Это могло бы повысить производительность предсказания на основе модели за счет возможного увеличения количества описательных параметров модели.
Другое изменение получают, отбрасывая предположение о стационарности стохастической модели сигнала. Тогда автокорреляционная функция становится функцией двух переменных 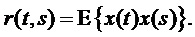 . Например, значимые нестационарные синусоидальные модели могут содержать амплитудную (АМ) и частотную (FM) модуляцию.
. Например, значимые нестационарные синусоидальные модели могут содержать амплитудную (АМ) и частотную (FM) модуляцию.
Кроме того, можно задействовать более детерминированную модель сигнала. Как будет видно в некоторых приводимых ниже примерах, такое предсказание может иметь исчезающе малую ошибку в некоторых случаях. В таких случаях можно избежать вероятностного подхода. Если предсказание является совершенным для всех сигналов в пространстве модели, нет необходимости в вычислении среднего значения производительности предсказания посредством вероятностной меры пространства рассматриваемой модели.
Ниже описываются различные особенности, касающиеся наборов модулированных фильтров. В частности, описываются особенности, оказывающие влияние на определение ковариационной матрицы, посредством чего обеспечиваются эффективные средства для определения коэффициентов предсказания предсказателя подполос.
Набор модулированных фильтров можно описать как содержащий двумерное индексное множество форм синтезируемых сигналов 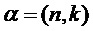 , где
, где 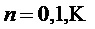 — индекс подполосы (полоса частот), и где
— индекс подполосы (полоса частот), и где 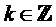 — индекс дискретного значения подполосы (временной интервал). Для простоты описания предполагается, что формы синтезируемых сигналов приведены в непрерывном времени и нормированы на единичный шаг по времени:
— индекс дискретного значения подполосы (временной интервал). Для простоты описания предполагается, что формы синтезируемых сигналов приведены в непрерывном времени и нормированы на единичный шаг по времени:
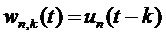 , (16)
, (16)
где
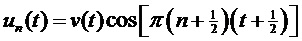 , (17)
, (17)
в случае набора косинусно-модулированных фильтров. Предполагается, что оконная функция 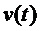 является вещественнозначной и четной. До незначительных изменений закона модуляции это охватывает диапазон случаев с высокой значимостью, таких как MDCT (модифицированное дискретное косинусное преобразование), QMF (квадратурный зеркальный фильтр) и ELT (расширенные перекрывающиеся преобразования) с L подполос при дискретизации с временным шагом
является вещественнозначной и четной. До незначительных изменений закона модуляции это охватывает диапазон случаев с высокой значимостью, таких как MDCT (модифицированное дискретное косинусное преобразование), QMF (квадратурный зеркальный фильтр) и ELT (расширенные перекрывающиеся преобразования) с L подполос при дискретизации с временным шагом 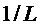 . Предполагается, что окно имеет конечную длительность или длину с несущим множеством в интервале
. Предполагается, что окно имеет конечную длительность или длину с несущим множеством в интервале 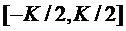 , где К — коэффициент перекрытия перекрывающегося преобразования, и где
, где К — коэффициент перекрытия перекрывающегося преобразования, и где 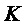 указывает длину оконной функции.
указывает длину оконной функции.
По причине структуры, инвариантной относительно сдвига, можно найти, что функцию взаимной корреляции формы синтезируемого сигнала (определенную в уравнении (4)) можно записать как:
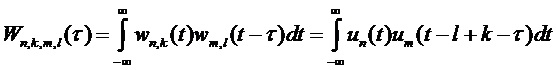 . (18)
. (18)
То есть 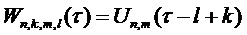 с учетом определения
с учетом определения 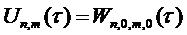 . Структура (17) модуляции допускает дальнейшее разложение в
. Структура (17) модуляции допускает дальнейшее разложение в
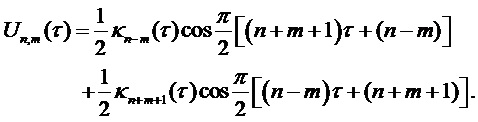 , (19)
, (19)
где кернфункция 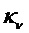 отображает дискретизацию с шагом по частоте подполосы набора фильтров, переменным в соответствии с распределением Вигнера-Вилле окна набора фильтров:
отображает дискретизацию с шагом по частоте подполосы набора фильтров, переменным в соответствии с распределением Вигнера-Вилле окна набора фильтров:
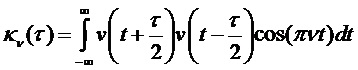 . (20)
. (20)
Ядро является вещественным и четным по 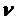 и
и 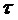 по причине вышеупомянутых предположений об оконной функции
по причине вышеупомянутых предположений об оконной функции 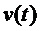 . Ее преобразование Фурье является произведением характеристик сдвинутых окон:
. Ее преобразование Фурье является произведением характеристик сдвинутых окон:
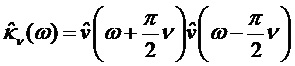 . (21)
. (21)
Из уравнений (20) и (21) видно, что ядро 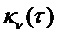 становится исчезающее малым для
становится исчезающее малым для 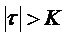 и обладает быстрым спадом в зависимости от
и обладает быстрым спадом в зависимости от 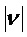 при типичном выборе окон
при типичном выборе окон 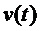 набора фильтров. Как следствие, вторым членом уравнения (19), включающим
набора фильтров. Как следствие, вторым членом уравнения (19), включающим 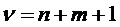 , часто можно пренебречь за исключением самых нижних подполос.
, часто можно пренебречь за исключением самых нижних подполос.
Для автокорреляционной функции 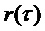 заданной модели сигнала вышеупомянутые формулы можно вставить в определения ковариационной матрицы дискретных значений подполос, заданной уравнением (3). Получим
заданной модели сигнала вышеупомянутые формулы можно вставить в определения ковариационной матрицы дискретных значений подполос, заданной уравнением (3). Получим 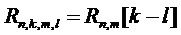 с определением
с определением
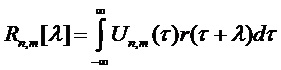 . (22)
. (22)
В зависимости от спектральной плотности мощности 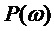 данной модели сигнала (которая соответствует преобразованию Фурье автокорреляционной функции
данной модели сигнала (которая соответствует преобразованию Фурье автокорреляционной функции 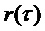 ) находим
) находим
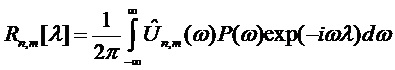 , (23)
, (23)
где 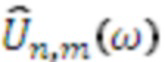 — преобразование Фурье
— преобразование Фурье 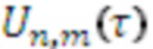 , где
, где 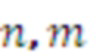 определяют индексы подполос, и где
определяют индексы подполос, и где 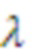 представляет запаздывание интервала времени (
представляет запаздывание интервала времени (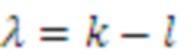 ). Выражение из уравнения (23) можно переписать как
). Выражение из уравнения (23) можно переписать как
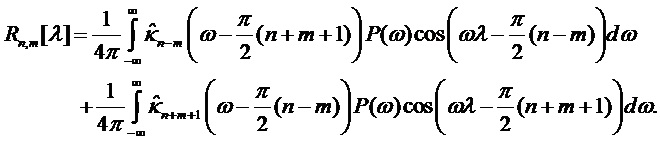 (24)
(24)
Важное наблюдение заключается в том, что первый член уравнения (24) по существу обладает свойством инвариантности относительно сдвигов по частоте. Если пренебречь вторым членом уравнения (24) и сдвинуть 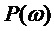 на целое число, в
на целое число, в 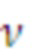 раз превышающее интервал между подполосами
раз превышающее интервал между подполосами 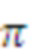 , до
, до 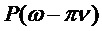 , можно найти соответствующий сдвиг в ковариациях
, можно найти соответствующий сдвиг в ковариациях 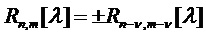 , где знак зависит от (целочисленных) значений запаздывания по времени
, где знак зависит от (целочисленных) значений запаздывания по времени 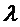 . Это отражает преимущество использования набора фильтров с модулированной структурой в сравнении с общим случаем набора фильтров.
. Это отражает преимущество использования набора фильтров с модулированной структурой в сравнении с общим случаем набора фильтров.
Уравнение (24) обеспечивает эффективные средства для определения матричных коэффициентов ковариационной матрицы дискретных значений подполос, если известна PSD лежащей в ее основе модели сигнала. Например, в случае схемы предсказания на основе синусоидальной модели, использующей модель сигнала 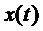 , содержащую единственную синусоиду с (угловой) частотой
, содержащую единственную синусоиду с (угловой) частотой 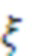 , PSD имеет вид:
, PSD имеет вид: 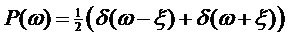 . Подстановка
. Подстановка 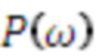 в уравнение (24) дает четыре члена, тремя из которых можно пренебречь в предположении, что
в уравнение (24) дает четыре члена, тремя из которых можно пренебречь в предположении, что 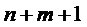 является большим числом. Остающийся член обращается в
является большим числом. Остающийся член обращается в
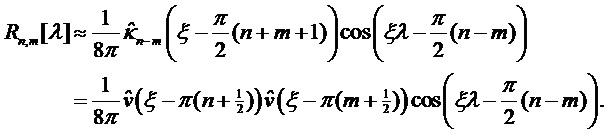 (25)
(25)
Уравнение (25) обеспечивает эффективные средства для определения ковариационной матрицы 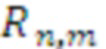 подполосы. Дискретное значение
подполосы. Дискретное значение 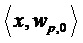 подполосы можно надежно предсказать при помощи совокупности окружающих дискретных значений
подполосы можно надежно предсказать при помощи совокупности окружающих дискретных значений 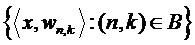 подполос, которые, как предполагается, оказывают значительное влияние на рассматриваемую частоту. Абсолютную частоту
подполос, которые, как предполагается, оказывают значительное влияние на рассматриваемую частоту. Абсолютную частоту 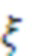 можно выразить в относительном выражении, по отношению к центральной частоте
можно выразить в относительном выражении, по отношению к центральной частоте 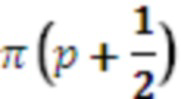 подполосы, как
подполосы, как 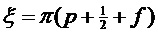 , где
, где 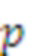 — индекс подполосы для подполосы, содержащей частоту
— индекс подполосы для подполосы, содержащей частоту 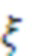 , и где
, и где 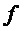 — параметр нормированной частоты, принимающий значения от –0,5 до +0,5 и указывающий положение частоты
— параметр нормированной частоты, принимающий значения от –0,5 до +0,5 и указывающий положение частоты 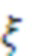 относительно центральной частоты подполосы
относительно центральной частоты подполосы 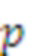 . Установив ковариационную матрицу подполосы
. Установив ковариационную матрицу подполосы 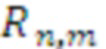 , коэффициенты предсказателя
, коэффициенты предсказателя 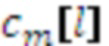 , применяемые к дискретному значению подполосы в подполосе m с индексом дискретного значения l для оценки дискретного значения подполосы в подполосе n с индексом дискретного значения k, находят, решая нормальные уравнения (7), которые в рассматриваемом случае можно записать как
, применяемые к дискретному значению подполосы в подполосе m с индексом дискретного значения l для оценки дискретного значения подполосы в подполосе n с индексом дискретного значения k, находят, решая нормальные уравнения (7), которые в рассматриваемом случае можно записать как
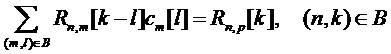 . (26)
. (26)
В уравнении (26) множество  описывает несущее множество маски предсказания, проиллюстрированное, например, на фиг. 2. Иными словами, множество
описывает несущее множество маски предсказания, проиллюстрированное, например, на фиг. 2. Иными словами, множество  определяет подполосы m и индексы l дискретных значений, используемые для предсказания целевого дискретного значения.
определяет подполосы m и индексы l дискретных значений, используемые для предсказания целевого дискретного значения.
Ниже иллюстративным образом представлены решения нормальных уравнений (26) для различных несущих множеств маски предсказания (как показано на фиг. 2). Пример причинного внутриполосного предсказателя второго порядка получен путем выбора несущего множества маски предсказания 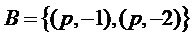 . Такое несущее множество маски предсказания соответствует маске 202 предсказания по фиг. 2. Нормальные уравнения (26) для этого предсказания с двумя ответвлениями при использовании приближения по уравнению (25) обращаются в
. Такое несущее множество маски предсказания соответствует маске 202 предсказания по фиг. 2. Нормальные уравнения (26) для этого предсказания с двумя ответвлениями при использовании приближения по уравнению (25) обращаются в
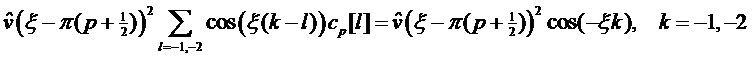 . (27)
. (27)
Решение уравнения (27) имеет вид 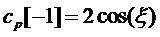 ,
, 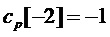 , и является единственным до тех пор, пока частота
, и является единственным до тех пор, пока частота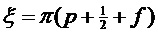 не будет выбрана так, что
не будет выбрана так, что 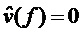 . Можно найти, что среднее значение квадратичной ошибки предсказания в соответствии с уравнением (6) является исчезающе малым. Следовательно, синусоидальное предсказание является совершенным с точностью приближения уравнения (25). Свойство инвариантности относительно сдвигов по частоте здесь проиллюстрировано тем, что при использовании определения
. Можно найти, что среднее значение квадратичной ошибки предсказания в соответствии с уравнением (6) является исчезающе малым. Следовательно, синусоидальное предсказание является совершенным с точностью приближения уравнения (25). Свойство инвариантности относительно сдвигов по частоте здесь проиллюстрировано тем, что при использовании определения 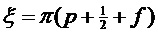 коэффициент
коэффициент 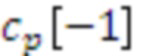 предсказания можно переписать в выражении нормированной частоты f как
предсказания можно переписать в выражении нормированной частоты f как 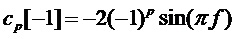 . Это означает, что коэффициенты предсказания зависят только от нормированной частоты
. Это означает, что коэффициенты предсказания зависят только от нормированной частоты 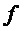 в пределах отдельной подполосы. Абсолютные значения коэффициентов предсказания, однако, не зависят от индекса
в пределах отдельной подполосы. Абсолютные значения коэффициентов предсказания, однако, не зависят от индекса 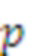 подполосы.
подполосы.
Как обсуждалось выше для фиг. 4, внутриполосное предсказание имеет некоторые недостатки в отношении артефактов паразитных частот при ограничении шума. Следующий пример относится к улучшенному поведению, проиллюстрированному на фиг. 5. Причинное межполосное предсказание, как следует из настоящего документа, получают, выбирая несущее множество маски предсказания 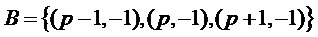 , требующее лишь одного более раннего временного интервала вместо двух и выполняющее ограничение шума с меньшими вкладами паразитных частот, чем для классической маски 202 предсказания из первого примера. Несущее множество маски предсказания
, требующее лишь одного более раннего временного интервала вместо двух и выполняющее ограничение шума с меньшими вкладами паразитных частот, чем для классической маски 202 предсказания из первого примера. Несущее множество маски предсказания 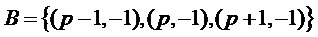 соответствует маске 203 предсказания по фиг. 2. Нормальные уравнения (26), основанные на приближении уравнения (25), сокращаются в данном случае до двух уравнений для трех неизвестных коэффициентов
соответствует маске 203 предсказания по фиг. 2. Нормальные уравнения (26), основанные на приближении уравнения (25), сокращаются в данном случае до двух уравнений для трех неизвестных коэффициентов 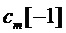 ,
, 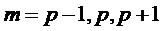 :
:
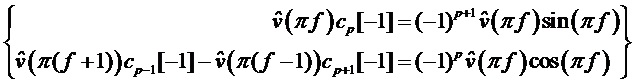 . (28)
. (28)
Можно найти, что любое решение уравнений (28) приводит к стремлению к нулю среднего значения квадратичной ошибки предсказания в соответствии с уравнением (6). Возможной стратегией выбора одного решения среди бесконечного количества решений уравнений (28) является минимизация суммы квадратов коэффициентов предсказания. Это приводит к коэффициентам, имеющим вид:
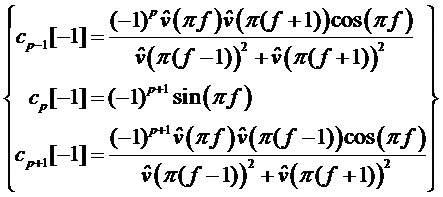 . (29)
. (29)
Из формул (29) видно, что коэффициенты предсказания зависят только от нормированной частоты 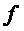 относительно средней точки целевой подполосы
относительно средней точки целевой подполосы 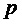 , а также зависят от четности целевой подполосы
, а также зависят от четности целевой подполосы 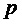 .
.
Используя то же несущее множество маски предсказания 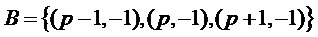 для предсказания трех дискретных значений
для предсказания трех дискретных значений 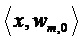 подполос для
подполос для 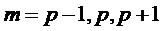 , как проиллюстрировано маской 204 предсказания по фиг. 2, получают матрицу предсказания размера 3×3. При введении более естественной стратегии во избежание неопределенности в нормальных уравнениях, а именно подставляя ослабленную синусоидальную модель
, как проиллюстрировано маской 204 предсказания по фиг. 2, получают матрицу предсказания размера 3×3. При введении более естественной стратегии во избежание неопределенности в нормальных уравнениях, а именно подставляя ослабленную синусоидальную модель 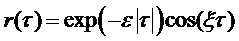 , соответствующую
, соответствующую 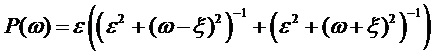 , численные вычисления приводят к элементам матрицы предсказания размера 3×3 по фиг. 3. Элементы матрицы предсказания показаны в зависимости от нормированной частоты
, численные вычисления приводят к элементам матрицы предсказания размера 3×3 по фиг. 3. Элементы матрицы предсказания показаны в зависимости от нормированной частоты 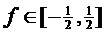 в случае перекрытия
в случае перекрытия 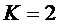 с синусоидальной оконной функцией
с синусоидальной оконной функцией 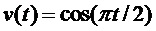 и в случае нечетной подполосы
и в случае нечетной подполосы 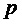 .
.
Таким образом, было показано, что для описания характеристик, лежащих в основе подлежащего кодированию входного звукового сигнала, можно использовать модели сигнала 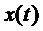 . Параметры, описывающие автокорреляционную функцию
. Параметры, описывающие автокорреляционную функцию 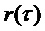 , можно передавать в декодер 100, посредством этого делая возможным вычисление декодером 100 предсказателя исходя из переданных параметров и из знания модели сигнала
, можно передавать в декодер 100, посредством этого делая возможным вычисление декодером 100 предсказателя исходя из переданных параметров и из знания модели сигнала 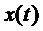 . Было показано, что для наборов модулированных фильтров можно получить эффективные средства для определения ковариационной матрицы подполос модели сигнала и для решения нормальных уравнений с целью определения коэффициентов предсказателя. В частности, было показано, что результирующие коэффициенты предсказателя являются инвариантными относительно сдвигов подполос и, как правило, зависят только от нормированной частоты относительно конкретной подполосы. В результате можно предусмотреть предварительно определяемые справочные таблицы (такие как таблица, проиллюстрированная на фиг. 3), позволяющие определять коэффициенты предсказателя, зная нормированную частоту
. Было показано, что для наборов модулированных фильтров можно получить эффективные средства для определения ковариационной матрицы подполос модели сигнала и для решения нормальных уравнений с целью определения коэффициентов предсказателя. В частности, было показано, что результирующие коэффициенты предсказателя являются инвариантными относительно сдвигов подполос и, как правило, зависят только от нормированной частоты относительно конкретной подполосы. В результате можно предусмотреть предварительно определяемые справочные таблицы (такие как таблица, проиллюстрированная на фиг. 3), позволяющие определять коэффициенты предсказателя, зная нормированную частоту 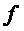 , не зависящую (без учета значения четности) от индекса
, не зависящую (без учета значения четности) от индекса 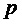 подполосы, для которой определяются эти коэффициенты предсказателя.
подполосы, для которой определяются эти коэффициенты предсказателя.
Ниже в дальнейших подробностях описывается предсказание на основе периодической модели с применением единственной основной частоты  . Автокорреляционная функция
. Автокорреляционная функция 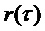 такой периодической модели имеет вид уравнения (13). Эквивалентная PSD, или линейчатый спектр, имеет вид:
такой периодической модели имеет вид уравнения (13). Эквивалентная PSD, или линейчатый спектр, имеет вид:
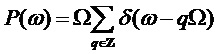 . (30)
. (30)
Когда период 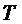 периодической модели является достаточно малым, например
периодической модели является достаточно малым, например 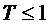 , основная частота
, основная частота 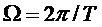 является достаточно большой, чтобы сделать возможным применение синусоидальной модели, полученной выше с применением частоты гармоники
является достаточно большой, чтобы сделать возможным применение синусоидальной модели, полученной выше с применением частоты гармоники 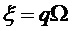 , ближайшей к центральной частоте
, ближайшей к центральной частоте 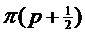 подполосы
подполосы 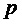 подлежащего предсказанию целевого дискретного значения подполосы. Это означает, что с применением вышеописанной синусоидальной модели можно верно смоделировать и предсказать периодические сигналы, имеющие малый период
подлежащего предсказанию целевого дискретного значения подполосы. Это означает, что с применением вышеописанной синусоидальной модели можно верно смоделировать и предсказать периодические сигналы, имеющие малый период 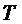 , т.е. период, являющийся малым относительно временного шага набора фильтров.
, т.е. период, являющийся малым относительно временного шага набора фильтров.
Когда период 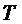 является достаточно большим по сравнению с длительностью
является достаточно большим по сравнению с длительностью 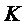 окна
окна 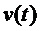 набора фильтров, предсказатель уменьшается до приближения задержки на
набора фильтров, предсказатель уменьшается до приближения задержки на 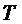 . Как будет показано, коэффициенты этого предсказателя можно считывать непосредственно из функции взаимной корреляции форм сигналов, имеющей вид уравнения (19).
. Как будет показано, коэффициенты этого предсказателя можно считывать непосредственно из функции взаимной корреляции форм сигналов, имеющей вид уравнения (19).
Вставка модели в соответствии с уравнением (13) в уравнение (22) приводит к уравнению
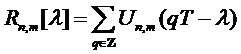 , (31)
, (31)
Важным наблюдением является то, что если 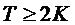 , то для каждой
, то для каждой 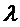 ненулевым является самое большее один член уравнения (31), поскольку
ненулевым является самое большее один член уравнения (31), поскольку 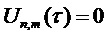 для
для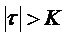 . Выбирая несущее множество маски предсказания
. Выбирая несущее множество маски предсказания 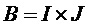 с диаметром временного интервала
с диаметром временного интервала 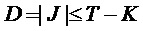 , можно наблюдать, что
, можно наблюдать, что 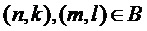 предполагает
предполагает 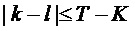 , и поэтому единственным членом уравнения (31) является член, для которого
, и поэтому единственным членом уравнения (31) является член, для которого 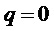 . Из этого следует, что
. Из этого следует, что 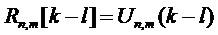 , что представляет собой скалярное произведение ортогональных форм сигналов и что стремится к нулю как при
, что представляет собой скалярное произведение ортогональных форм сигналов и что стремится к нулю как при 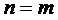 , так и при
, так и при 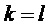 . В общем, нормальные уравнения (7) обращаются в
. В общем, нормальные уравнения (7) обращаются в
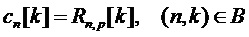 . (32)
. (32)
Несущее множество маски предсказания можно выбрать так, чтобы оно было центрировано около 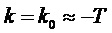 , и в этом случае правая сторона уравнения (32) вносит свой единственный вклад от
, и в этом случае правая сторона уравнения (32) вносит свой единственный вклад от 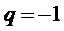 . Тогда коэффициенты имеют вид:
. Тогда коэффициенты имеют вид:
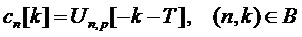 , (33)
, (33)
при этом можно подставить выражение в явном виде из уравнения (19). Геометрия несущего множества маски предсказания в этом случае могла бы иметь внешний вид несущего множества маски предсказания для маски 205 предсказания по фиг. 2. Среднее значение квадратичной ошибки предсказания, имеющей вид уравнения (6), равно квадратичной норме проекции 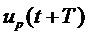 на интервал, охватываемый дополнением приблизительных форм сигналов
на интервал, охватываемый дополнением приблизительных форм сигналов 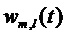 ,
, 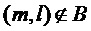 .
.
Ввиду вышесказанного из настоящего документа следует, что дискретное значение 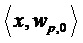 подполосы (в подполосе p и с временным индексом 0) можно предсказать, используя подходящее несущее множество
подполосы (в подполосе p и с временным индексом 0) можно предсказать, используя подходящее несущее множество 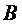 маски предсказания, центрированное около
маски предсказания, центрированное около 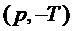 , с временным диаметром, приблизительно равным Т. Нормальные уравнения можно решать для каждого значения Т и р. Иными словами, для каждой периодичности Т входного звукового сигнала и для каждой подполосы р коэффициенты предсказания при заданном несущем множестве В маски предсказания можно определить, используя нормальные уравнения (33).
, с временным диаметром, приблизительно равным Т. Нормальные уравнения можно решать для каждого значения Т и р. Иными словами, для каждой периодичности Т входного звукового сигнала и для каждой подполосы р коэффициенты предсказания при заданном несущем множестве В маски предсказания можно определить, используя нормальные уравнения (33).
При большом количестве подполос р и широком интервале периодов Т сведение в таблицу всех коэффициентов предсказателя напрямую является непрактичным. Но в случае, подобном случаю с синусоидальной моделью, модулированная структура набора фильтров предполагает значительное уменьшение необходимого размера таблицы посредством свойства инвариантности относительно сдвигов по частоте. Как правило, достаточно изучить сдвинутую гармоническую модель с параметром сдвига  , центрированную около центра подполосы р, т.е. центрированную около
, центрированную около центра подполосы р, т.е. центрированную около 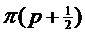 , определяемую подмножеством
, определяемую подмножеством 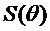 положительных частот из совокупности частот
положительных частот из совокупности частот 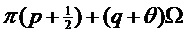 ,
, 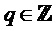 ,
,
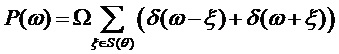 . (34)
. (34)
Действительно, при заданном Т и достаточно большом индексе р подполосы, периодическую модель в соответствии с уравнением (30) можно воспроизвести с хорошим приближением посредством сдвинутой модели в соответствии с уравнением (34) путем подходящего выбора параметра 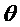 сдвига. Вставка уравнения (34) в уравнение (24) при
сдвига. Вставка уравнения (34) в уравнение (24) при 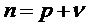 и
и 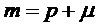 (при этом
(при этом 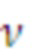 и
и 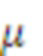 определяют индексы подполос около подполосы р из несущего множества маски предсказания) и преобразования на основе анализа Фурье приводят к следующему выражению для ковариационной матрицы:
определяют индексы подполос около подполосы р из несущего множества маски предсказания) и преобразования на основе анализа Фурье приводят к следующему выражению для ковариационной матрицы:
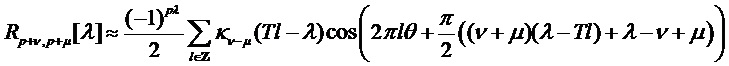 . (35)
. (35)
Как видно, выражение (35) зависит от индекса р целевой подполосы только посредством коэффициента 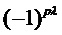 . Для случая большого периода Т и малого временного запаздывания
. Для случая большого периода Т и малого временного запаздывания 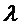 в выражение (35) вносит вклад только первый член для l=0, и снова можно найти, что ковариационная матрица представляет собой единичную матрицу. Тогда правая сторона нормальных уравнений (26) для подходящего несущего множества В маски предсказания, центрированного около
в выражение (35) вносит вклад только первый член для l=0, и снова можно найти, что ковариационная матрица представляет собой единичную матрицу. Тогда правая сторона нормальных уравнений (26) для подходящего несущего множества В маски предсказания, центрированного около 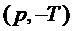 , дает коэффициенты предсказания непосредственно как
, дает коэффициенты предсказания непосредственно как
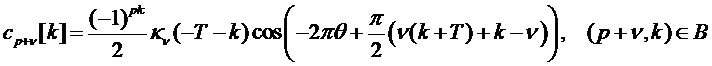 . (36)
. (36)
Это воспроизводит вклад первого члена уравнений (19)-(33) с каноническим выбором сдвига 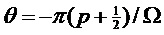 .
.
Уравнение (36) позволяет определять коэффициенты 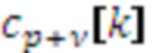 предсказания для подполосы
предсказания для подполосы 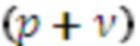 с временным индексом
с временным индексом 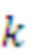 , при этом подлежащее предсказанию дискретное значение представляет собой дискретное значение из подполосы
, при этом подлежащее предсказанию дискретное значение представляет собой дискретное значение из подполосы 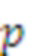 с временным индексом 0. Как видно из уравнения (36), коэффициенты
с временным индексом 0. Как видно из уравнения (36), коэффициенты 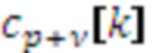 предсказания зависят от индекса р целевой подполосы только посредством коэффициента
предсказания зависят от индекса р целевой подполосы только посредством коэффициента 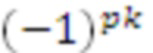 , который влияет на знак коэффициента предсказания. Абсолютное значение коэффициента предсказания, однако, не зависит от индекса р целевой подполосы. С другой стороны, коэффициент
, который влияет на знак коэффициента предсказания. Абсолютное значение коэффициента предсказания, однако, не зависит от индекса р целевой подполосы. С другой стороны, коэффициент 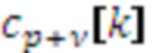 предсказания зависит от периодичности Т и от параметра
предсказания зависит от периодичности Т и от параметра 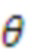 сдвига. Кроме того, коэффициент
сдвига. Кроме того, коэффициент 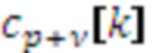 предсказания зависит от
предсказания зависит от 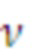 и
и 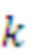 , т.е. от несущего множества В маски предсказания, используемого для предсказания целевого дискретного значения в целевой подполосе р.
, т.е. от несущего множества В маски предсказания, используемого для предсказания целевого дискретного значения в целевой подполосе р.
В настоящем документе предлагается создавать справочную таблицу, позволяющую отыскивать набор коэффициентов 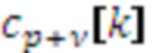 предсказания для предварительно определенного несущего множества В маски предсказания. Для данного несущего множества В маски предсказания справочная таблица предусматривает набор коэффициентов
предсказания для предварительно определенного несущего множества В маски предсказания. Для данного несущего множества В маски предсказания справочная таблица предусматривает набор коэффициентов 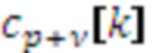 предсказания для предварительно определенного набора значений периодичности Т и значений параметра
предсказания для предварительно определенного набора значений периодичности Т и значений параметра 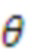 сдвига. С целью ограничения количества элементов справочной таблицы следует ограничить количество предварительно определенных значений периодичности Т и количество предварительно определенных значений параметра
сдвига. С целью ограничения количества элементов справочной таблицы следует ограничить количество предварительно определенных значений периодичности Т и количество предварительно определенных значений параметра 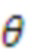 сдвига. Как видно из выражения (36) подходящая величина шага квантования для предварительно определенных значений периодичности Т и параметра
сдвига. Как видно из выражения (36) подходящая величина шага квантования для предварительно определенных значений периодичности Т и параметра 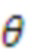 сдвига должна зависеть от периодичности Т. В частности, видно, что для относительно больших периодичностей Т (относительно длительности К оконной функции) можно использовать относительно большие шаги квантования для периодичности Т и параметра
сдвига должна зависеть от периодичности Т. В частности, видно, что для относительно больших периодичностей Т (относительно длительности К оконной функции) можно использовать относительно большие шаги квантования для периодичности Т и параметра 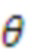 сдвига. В другом предельном случае для относительно малых периодичностей Т, стремящихся к нулю, нужно учитывать только один синусоидальный вклад, поэтому периодичность Т теряет свою важность. С другой стороны, формулы для синусоидального предсказания в соответствии с уравнением (29) требуют того, чтобы нормированный сдвиг по абсолютной частоте
сдвига. В другом предельном случае для относительно малых периодичностей Т, стремящихся к нулю, нужно учитывать только один синусоидальный вклад, поэтому периодичность Т теряет свою важность. С другой стороны, формулы для синусоидального предсказания в соответствии с уравнением (29) требуют того, чтобы нормированный сдвиг по абсолютной частоте 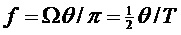 изменялся медленно, поэтому величину шага квантования для параметра
изменялся медленно, поэтому величину шага квантования для параметра 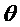 сдвига следует масштабировать на основе периодичности Т.
сдвига следует масштабировать на основе периодичности Т.
В общем, в настоящем документе предлагается использовать равномерное квантование периодичности Т с фиксированной величиной шага. Параметр 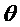 сдвига также можно квантовать равномерным образом, однако, с величиной шага, пропорциональной
сдвига также можно квантовать равномерным образом, однако, с величиной шага, пропорциональной 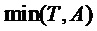 , где значение А зависит от специфики оконной функции набора фильтров. Более того, для Т<2 интервал параметров
, где значение А зависит от специфики оконной функции набора фильтров. Более того, для Т<2 интервал параметров 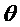 сдвига можно ограничить как
сдвига можно ограничить как 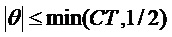 с некоторой постоянной С, отражающей некоторый предел сдвигов
с некоторой постоянной С, отражающей некоторый предел сдвигов 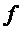 по абсолютной частоте.
по абсолютной частоте.
Фиг. 6а иллюстрирует один из примеров результирующей сетки квантования в плоскости 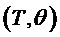 для А=2. Рассматривается только интервал
для А=2. Рассматривается только интервал 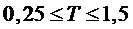 полной двумерной зависимости, в то время как для остального представляющего интерес интервала можно использовать по существу одномерные параметризации, заданные уравнениями (29) и уравнениями (36). В частности, для периодичностей Т, стремящихся к нулю (например, Т<0,25), предсказание на основе периодической модели по существу соответствует предсказанию на основе синусоидальной модели, и коэффициенты предсказания можно определить, используя формулы (29). С другой стороны, для периодичностей Т, существенно превышающих длительность окна K (например, Т>1,5), с применением уравнения (36) можно определить набор коэффициентов
полной двумерной зависимости, в то время как для остального представляющего интерес интервала можно использовать по существу одномерные параметризации, заданные уравнениями (29) и уравнениями (36). В частности, для периодичностей Т, стремящихся к нулю (например, Т<0,25), предсказание на основе периодической модели по существу соответствует предсказанию на основе синусоидальной модели, и коэффициенты предсказания можно определить, используя формулы (29). С другой стороны, для периодичностей Т, существенно превышающих длительность окна K (например, Т>1,5), с применением уравнения (36) можно определить набор коэффициентов 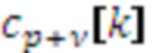 предсказания, использующих предсказание на основе периодической модели. Это уравнение можно переопределить путем подстановки
предсказания, использующих предсказание на основе периодической модели. Это уравнение можно переопределить путем подстановки 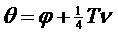 . Находим:
. Находим:
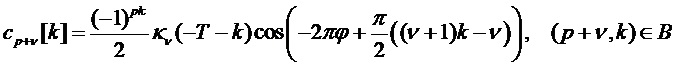 . (37)
. (37)
Отводя 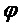 роль, приданную параметру
роль, приданную параметру 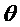 при сведении в таблицу, получается по существу раздельная структура в эквивалентной плоскости
при сведении в таблицу, получается по существу раздельная структура в эквивалентной плоскости 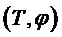 . С точностью до изменений знака в зависимости от индексов подполос и временных интервалов зависимость от Т содержится в первом, медленно меняющемся множителе, а зависимость от
. С точностью до изменений знака в зависимости от индексов подполос и временных интервалов зависимость от Т содержится в первом, медленно меняющемся множителе, а зависимость от 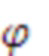 содержится в 1-периодичном втором множителе в уравнении (37).
содержится в 1-периодичном втором множителе в уравнении (37).
Модифицированный параметр 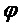 сдвига можно интерпретировать как сдвиг гармонического ряда в единицах основной частоты при измерении от средней точки средних точек исходного и целевого элементов разрешения. Преимущественным является сохранение этой модифицированной параметризации
сдвига можно интерпретировать как сдвиг гармонического ряда в единицах основной частоты при измерении от средней точки средних точек исходного и целевого элементов разрешения. Преимущественным является сохранение этой модифицированной параметризации 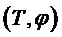 для всех значений периодичностей Т, поскольку симметрии в уравнении (37), очевидные в отношении одновременных изменений знака
для всех значений периодичностей Т, поскольку симметрии в уравнении (37), очевидные в отношении одновременных изменений знака 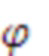 и
и  , будут в целом сохраняться, и их можно использовать для уменьшения размеров таблиц.
, будут в целом сохраняться, и их можно использовать для уменьшения размеров таблиц.
Как указано выше, фиг. 6а изображает двумерную сетку квантования, лежащую в основе табличных данных для вычисления предсказателя на основе периодической модели в наборе косинусно-модулированных фильтров. Эта модель сигнала является такой для сигнала с периодом Т 602, измеренным в единицах временного шага набора фильтров. Эквивалентно, эта модель содержит линии частот целочисленных множителей, также известные как гармоники, основной частоты, соответствующей периоду Т. Для каждой целевой подполосы параметр 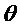 601 сдвига указывает расстояние от ближайшей гармоники до центральной частоты, измеренное в единицах основной частоты Ω. Параметр
601 сдвига указывает расстояние от ближайшей гармоники до центральной частоты, измеренное в единицах основной частоты Ω. Параметр 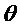 601 сдвига имеет значение –0,5-0,5. Черные кресты 603 на фиг. 6а иллюстрируют соответствующую плотность узловых точек квантования для сведения в таблицу предсказателей с высоким коэффициентом передачи предсказания на основе периодической модели. Для больших периодов (например, Т>2) сетка является равномерной. Повышенная плотность в параметре
601 сдвига имеет значение –0,5-0,5. Черные кресты 603 на фиг. 6а иллюстрируют соответствующую плотность узловых точек квантования для сведения в таблицу предсказателей с высоким коэффициентом передачи предсказания на основе периодической модели. Для больших периодов (например, Т>2) сетка является равномерной. Повышенная плотность в параметре 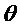 сдвига, как правило, требуется тогда, когда период Т уменьшается. Однако в области за пределами линий 604 расстояние
сдвига, как правило, требуется тогда, когда период Т уменьшается. Однако в области за пределами линий 604 расстояние 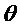 больше одного элемента разрешения по частоте набора фильтров, поэтому большинством узловых точек сетки в этой области можно пренебречь. Многоугольник 605 ограничивает область, достаточную для полного сведения в таблицу. В дополнение к наклонным линиям немного за пределами линий 604 представлены границы Т=0,25 и Т=1,5. Это возможно, поскольку с небольшими периодами 602 можно обращаться как с отельными синусоидами и поскольку предсказатели для больших периодов 602 можно аппроксимировать по существу одномерными таблицами, зависящими, главным образом, от параметра
больше одного элемента разрешения по частоте набора фильтров, поэтому большинством узловых точек сетки в этой области можно пренебречь. Многоугольник 605 ограничивает область, достаточную для полного сведения в таблицу. В дополнение к наклонным линиям немного за пределами линий 604 представлены границы Т=0,25 и Т=1,5. Это возможно, поскольку с небольшими периодами 602 можно обращаться как с отельными синусоидами и поскольку предсказатели для больших периодов 602 можно аппроксимировать по существу одномерными таблицами, зависящими, главным образом, от параметра 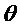 сдвига (или от модифицированного параметра
сдвига (или от модифицированного параметра 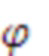 сдвига). Для варианта осуществления, проиллюстрированного на фиг. 6а, несущее множество маски предсказания, как правило, аналогично маске 205 предсказания по фиг. 2 для больших периодов Т.
сдвига). Для варианта осуществления, проиллюстрированного на фиг. 6а, несущее множество маски предсказания, как правило, аналогично маске 205 предсказания по фиг. 2 для больших периодов Т.
Фиг. 6b иллюстрирует предсказание на основе периодической модели в случае относительно больших периодов Т и в случае относительно малых периодов Т. Видно, что для больших периодов Т из верхней схемы, т.е. для относительно небольших основных частот Ω 613, оконная функция 612 набора фильтров захватывает относительно большое количество линий, или импульсов 616 Дирака, для PSD периодического сигнала. Импульсы 616 Дирака расположены при частотах 610 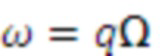 , где
, где 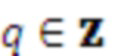 . Центральные частоты подполос набора фильтров расположены при частотах
. Центральные частоты подполос набора фильтров расположены при частотах 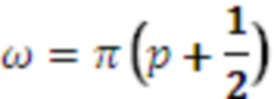 , где
, где 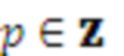 . Для заданной подполосы р расположение частоты импульса 616 с частотой
. Для заданной подполосы р расположение частоты импульса 616 с частотой 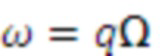 , ближайшей к центральной частоте данной подполосы
, ближайшей к центральной частоте данной подполосы 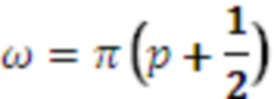 , можно описать в относительном выражении как
, можно описать в относительном выражении как 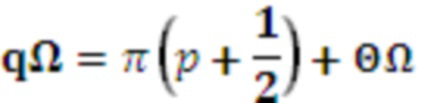 , с параметром
, с параметром 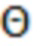 сдвига в интервале от –0,5 до +0,5. Как таковой, член
сдвига в интервале от –0,5 до +0,5. Как таковой, член 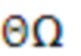 отражает расстояние (по частоте) от центральной частоты
отражает расстояние (по частоте) от центральной частоты 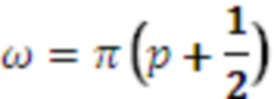 до ближайшей частотной составляющей 616 гармонической модели. Это проиллюстрировано верхней схемой по фиг. 6b, где центральной частотой является
до ближайшей частотной составляющей 616 гармонической модели. Это проиллюстрировано верхней схемой по фиг. 6b, где центральной частотой является 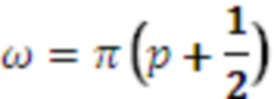 и где расстояние 618
и где расстояние 618 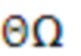 проиллюстрировано для случая относительно большого периода Т. Видно, что параметр
проиллюстрировано для случая относительно большого периода Т. Видно, что параметр 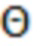 сдвига позволяет описывать весь гармонический ряд при рассмотрении в перспективе из центра подполосы
сдвига позволяет описывать весь гармонический ряд при рассмотрении в перспективе из центра подполосы 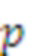 .
.
Нижняя схема по фиг. 6b иллюстрирует случай относительно малых периодов Т, т.е. относительно больших основных частот Ω 623, особенно основных частот 623, которые больше ширины окна 612. Видно, что в таких случаях оконная функция 612 может содержать только единственный импульс 626 периодического сигнала так, что сигнал можно рассматривать как синусоидальный сигнал в окне 612. Это означает, что для относительно малых периодов Т схема предсказания на основе периодической модели сходится к схеме предсказания на основе синусоидальной модели.
Фиг. 6b также иллюстрирует примеры масок 611, 621 предсказания, которые можно использовать соответственно для схемы предсказания на основе периодической модели и для схемы предсказания на основе синусоидальной модели. Маска 611 предсказания, используемая для схемы предсказания на основе периодической модели, может соответствовать маске 205 предсказания по фиг. 2 и может содержать несущее множество 614 маски предсказания для оценки целевого дискретного значения 615 подполосы. Маска 621 предсказания, используемая для схемы предсказания на основе синусоидальной модели, может соответствовать маске 203 предсказания по фиг. 2 и может содержать несущее множество 624 маски предсказания для оценки целевого дискретного значения 625 подполосы.
Фиг. 7а иллюстрирует пример способа 700 кодирования, включающий предсказание подполосы на основе модели с применением периодической модели (содержащей, например, единственную основную частоту Ω). Рассматривается кадр входного звукового сигнала. Для этого кадра можно определить (этап 701) периодичность Т или основную частоту Ω. Аудиокодер может содержать элементы декодера 100, проиллюстрированного на фиг. 1, в частности аудиокодер может содержать вычислитель 105 предсказателя и предсказатель 103 подполос. Периодичность Т или основную частоту Ω можно определить так, чтобы среднее значение сигналов 111 подполос квадратичных ошибок предсказания в соответствии с уравнением (6) уменьшалось (например, минимизировалось). Для примера, аудиокодер может применять подход «грубой силы», определяющий сигналы 111 подполос ошибок предсказания с применением различных основных частот Ω и определяющий основную частоту Ω, для которой среднее значение сигналов 111 подполос квадратичных ошибок предсказания уменьшается (например, минимизируется). Этот способ продолжается квантованием результирующих сигналов 111 подполос ошибок предсказания (этап 702). Кроме того, способ включает этап генерирования 703 битового потока, содержащего информацию, служащую признаком определенной основной частоты Ω и квантованных сигналов 111 подполос ошибок предсказания.
При определении основной частоты Ω на этапе 701, аудиокодер может использовать уравнения (36) и/или (29) с целью определения коэффициентов предсказания для конкретной основной частоты Ω. Набор возможных основных частот Ω может быть ограничен количеством битов, доступных для передачи информации, служащей признаком определенной основной частоты Ω.
Следует отметить, что система кодирования звука может использовать предварительно определенную модель (например, периодическую модель, содержащую единственную основную частоту Ω, или любую другую из моделей, представленных в настоящем документе) и/или предварительно определенную маску 202, 203, 204, 205 предсказания. С другой стороны, система кодирования звука может быть снабжена дополнительными степенями свободы путем предоставления аудиокодеру возможности определения соответствующей модели и/или соответствующей маски предсказания для подлежащего кодированию звукового сигнала. Информацию относительно выбранной модели и/или выбранной маски предсказания затем кодируют в битовом потоке и доставляют в соответствующий декодер 100.
Фиг. 7b иллюстрирует один из примеров способа 710 декодирования звукового сигнала, который был закодирован с применением предсказания на основе модели. Предполагается, что декодер 100 осведомлен о модели сигнала и маске предсказания, использованных кодером (либо посредством принятого битового потока, либо по причине предварительно определенных установок). Кроме того, в иллюстративных целях предполагается, что была использована периодическая модель предсказания. Декодер 100 извлекает из принятого битового потока информацию относительно основной частоты Ω (этап 711). Используя информацию относительно основной частоты Ω, декодер 100 может определять периодичность Т. Основную частоту Ω и/или периодичность Т можно использовать для определения набора коэффициентов предсказания для разных предсказателей подполос (этап 712). Предсказатели подполос можно использовать для определения оценочных сигналов подполос (этап 713), которые объединяют с деквантованными сигналами 111 подполос ошибок предсказания, получая декодированные сигналы 113 подполос. Декодированные сигналы 113 подполос можно подвергнуть фильтрации (этап 715) с применением набора 102 синтезирующих фильтров, посредством этого получая декодированный звуковой сигнал 114 во временной области.
Вычислитель 105 предсказателя может использовать уравнения (36) и/или (29) для определения коэффициентов предсказания для предсказателей 103 подполос на основе принятой информации относительно основной частоты Ω (этап 712). Это можно выполнить эффективно, используя справочную таблицу, проиллюстрированную на фиг. 6а и 3. Для примера, вычислитель 105 предсказателя может определять периодичность Т и определять, лежит ли эта периодичность ниже предварительно определенного нижнего порогового значения (например, Т=0,25). Если это так, то используется схема предсказания на основе синусоидальной модели. Это означает, что на основе принятой основной частоты Ω определяются подполосы р, содержащие кратную частоту 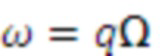 , где
, где 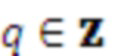 , основной частоты. Затем с применением отношения
, основной частоты. Затем с применением отношения 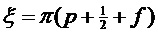 определяется нормированная частота f, где частота
определяется нормированная частота f, где частота 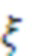 соответствует кратной частоте
соответствует кратной частоте 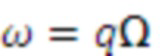 , лежащей в подполосе р. Вычислитель 105 предсказателя может затем использовать уравнение (29) или предварительно вычисленную справочную таблицу для определения набора коэффициентов предсказания (с применением маски 203 предсказания по фиг. 2 или маски 621 предсказания по фиг. 6b).
, лежащей в подполосе р. Вычислитель 105 предсказателя может затем использовать уравнение (29) или предварительно вычисленную справочную таблицу для определения набора коэффициентов предсказания (с применением маски 203 предсказания по фиг. 2 или маски 621 предсказания по фиг. 6b).
Следует отметить, что для каждой подполосы можно определять отличающийся набор коэффициентов предсказания. Однако в случае схемы предсказания на основе синусоидальной модели набор коэффициентов предсказания, как правило, определяется только для подполос р, находящихся под значительным воздействием кратной частоты 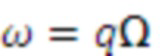 , где
, где 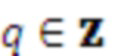 , основной частоты. Для других подполос коэффициенты предсказания не определяются, что означает, что оценочные сигналы 112 подполос для таких других подполос являются нулевыми.
, основной частоты. Для других подполос коэффициенты предсказания не определяются, что означает, что оценочные сигналы 112 подполос для таких других подполос являются нулевыми.
Для того чтобы уменьшить вычислительную сложность декодера 100 (и кодера, использующего такой же вычислитель 105 предсказателя), вычислитель 105 предсказателя может использовать предварительно определенную справочную таблицу, предоставляющую набор коэффициентов предсказания, обусловленных значениями Т и  . В частности, вычислитель 105 предсказателя может использовать ряд справочных таблиц для ряда разных значений Т. Каждая таблица из ряда справочных таблиц представляет отличающийся набор коэффициентов предсказания для ряда разных значений параметра
. В частности, вычислитель 105 предсказателя может использовать ряд справочных таблиц для ряда разных значений Т. Каждая таблица из ряда справочных таблиц представляет отличающийся набор коэффициентов предсказания для ряда разных значений параметра  сдвига.
сдвига.
В практической реализации ряд справочных таблиц может быть предусмотрен для разных значений параметра Т периода. Для примера, справочные таблицы можно предусмотреть для значений Т в интервале 0,25-2,5 (как проиллюстрировано на фиг. 6а). Справочные таблицы могут быть предусмотрены для предварительно определенной степени разбиения, или величины шага, различных параметров Т периода. В одной из иллюстративных реализаций величина шага для нормированного параметра Т периода составляет 1/16, и для T=8/32-80/32 предусмотрены разные справочные таблицы для квантованных коэффициентов предсказания. Таким образом, может быть предусмотрено всего 37 разных справочных таблиц. Каждая таблица может предусматривать квантованные коэффициенты предсказания в зависимости от параметра  сдвига или в зависимости от модифицированного параметра
сдвига или в зависимости от модифицированного параметра  сдвига. Справочные таблицы для T=8/32-80/32 можно использовать для интервала с приращением на половину величины шага, т.е.
сдвига. Справочные таблицы для T=8/32-80/32 можно использовать для интервала с приращением на половину величины шага, т.е. 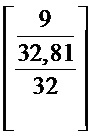 . Для заданной периодичности, отличающейся от доступных периодичностей, для которых были определены справочные таблицы, можно использовать справочную таблицу для ближайшей доступной периодичности.
. Для заданной периодичности, отличающейся от доступных периодичностей, для которых были определены справочные таблицы, можно использовать справочную таблицу для ближайшей доступной периодичности.
Как было описано выше, для длинных периодов Т (например, для периодов Т, превышающих период, для которого определена справочная таблица) можно использовать уравнение (36). В качестве альтернативы, для периодов Т, превышающих периоды, для которых были определены справочные таблицы, например для периодов Т>81/32, период Т можно разделить на целочисленную задержку Ti и на остаточную задержку Tr так, что T=Ti+Tr. Это разделение может быть таким, что остаточная задержка Tr будет лежать в пределах интервала, для которого применимо уравнение (36) и для которого доступны справочные таблицы, например, в пределах интервала [1,5, 2,5] или [49/32, 81/32] для приведенного выше примера. Действуя таким образом, можно определять коэффициенты предсказания с применением справочной таблицы для остаточной задержки Tr, и предсказатель 103 подполос может действовать на буфере 104 подполос, который был задержан на величину целочисленной задержки Ti. Например, если период T=3,7, то целочисленная задержка может составлять Ti=2, и за ней следует остаточная задержка Tr=1,7. Предсказатель может применяться на основе коэффициентов для Tr=1,7 на буфере сигналов, (дополнительно) задержанном на Ti=2.
Этот подход разделения полагается на разумное предположение о том, что экстрактор аппроксимирует задержку посредством Т в интервале [1,5, 2,5] или [49/32, 81/32]. Преимущество процедуры разделения по сравнению с применением уравнения (36) заключается в том, что коэффициенты предсказания можно определять в вычислительно эффективных операциях на справочных таблицах.
Как было описано выше, для коротких периодов (T<0,25) при определении коэффициентов предсказания можно использовать уравнение (29). В качестве альтернативы, может быть полезно использование (уже доступных) справочных таблиц (с целью уменьшения вычислительной сложности). Было сделано наблюдение, что модифицированный параметр 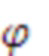 сдвига ограничен интервалом
сдвига ограничен интервалом 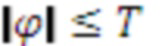 с величиной шага дискретизации
с величиной шага дискретизации 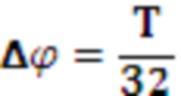 (для T<0,25 и для C=1, A=1/2).
(для T<0,25 и для C=1, A=1/2).
В настоящем документе предложено повторно использовать справочную таблицу для самого нижнего периода Т=0,25 посредством масштабирования модифицированного параметра 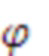 сдвига коэффициентом
сдвига коэффициентом 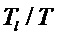 , при этом
, при этом 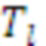 соответствует самому нижнему периоду, для которого доступна справочная таблица (например, Tl=0,25). Для примера, при Т = 0,1 и
соответствует самому нижнему периоду, для которого доступна справочная таблица (например, Tl=0,25). Для примера, при Т = 0,1 и 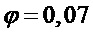 таблицу для T=0,25 можно запросить с повторно масштабированным параметром
таблицу для T=0,25 можно запросить с повторно масштабированным параметром 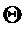 сдвига. Действуя таким образом, также можно вычислительно эффективно определять коэффициенты предсказания для коротких периодов (T<0,25) с применением операций поиска в таблицах. Кроме того, можно уменьшить требования к памяти предсказателя, так как можно уменьшить количество справочных таблиц.
сдвига. Действуя таким образом, также можно вычислительно эффективно определять коэффициенты предсказания для коротких периодов (T<0,25) с применением операций поиска в таблицах. Кроме того, можно уменьшить требования к памяти предсказателя, так как можно уменьшить количество справочных таблиц.
В настоящем документе была описана схема предсказания подполос на основе модели. Схема предсказания подполос на основе модели делает возможным эффективное описание предсказателей подполос, т.е. описание, требующее лишь относительно небольшого количества битов. Как результат эффективного описания предсказателей подполос можно использовать схемы межполосного предсказания подполос, ведущие к уменьшению артефактов паразитных частот. В целом, это делает возможным создание аудиокодеров с низкой битовой скоростью передачи данных, использующих предсказание подполос.
| название | год | авторы | номер документа |
|---|---|---|---|
| ПРЕДСКАЗАНИЕ НА ОСНОВЕ МОДЕЛИ В НАБОРЕ ФИЛЬТРОВ С КРИТИЧЕСКОЙ ДИСКРЕТИЗАЦИЕЙ | 2014 |
|
RU2636093C2 |
| ПРЕДСКАЗАНИЕ НА ОСНОВЕ МОДЕЛИ В НАБОРЕ ФИЛЬТРОВ С КРИТИЧЕСКОЙ ДИСКРЕТИЗАЦИЕЙ | 2014 |
|
RU2742460C2 |
| ЗВУКОВЫЕ КОДИРУЮЩЕЕ УСТРОЙСТВО И ДЕКОДИРУЮЩЕЕ УСТРОЙСТВО | 2014 |
|
RU2630887C2 |
| ЗВУКОВЫЕ КОДИРУЮЩЕЕ УСТРОЙСТВО И ДЕКОДИРУЮЩЕЕ УСТРОЙСТВО | 2014 |
|
RU2740359C2 |
| ЗВУКОВЫЕ КОДИРУЮЩЕЕ УСТРОЙСТВО И ДЕКОДИРУЮЩЕЕ УСТРОЙСТВО | 2014 |
|
RU2740690C2 |
| ЗВУКОВЫЕ КОДИРУЮЩЕЕ УСТРОЙСТВО И ДЕКОДИРУЮЩЕЕ УСТРОЙСТВО | 2020 |
|
RU2828411C2 |
| УСОВЕРШЕНСТВОВАННЫЙ КВАНТОВАТЕЛЬ | 2021 |
|
RU2823174C2 |
| УСОВЕРШЕНСТВОВАННЫЙ КВАНТОВАТЕЛЬ | 2017 |
|
RU2752127C2 |
| УСОВЕРШЕНСТВОВАННЫЙ КВАНТОВАТЕЛЬ | 2014 |
|
RU2640722C2 |
| МНОГОКАНАЛЬНЫЙ АУДИОКОДЕР БЕЗ ПОТЕРЬ | 2005 |
|
RU2387023C2 |
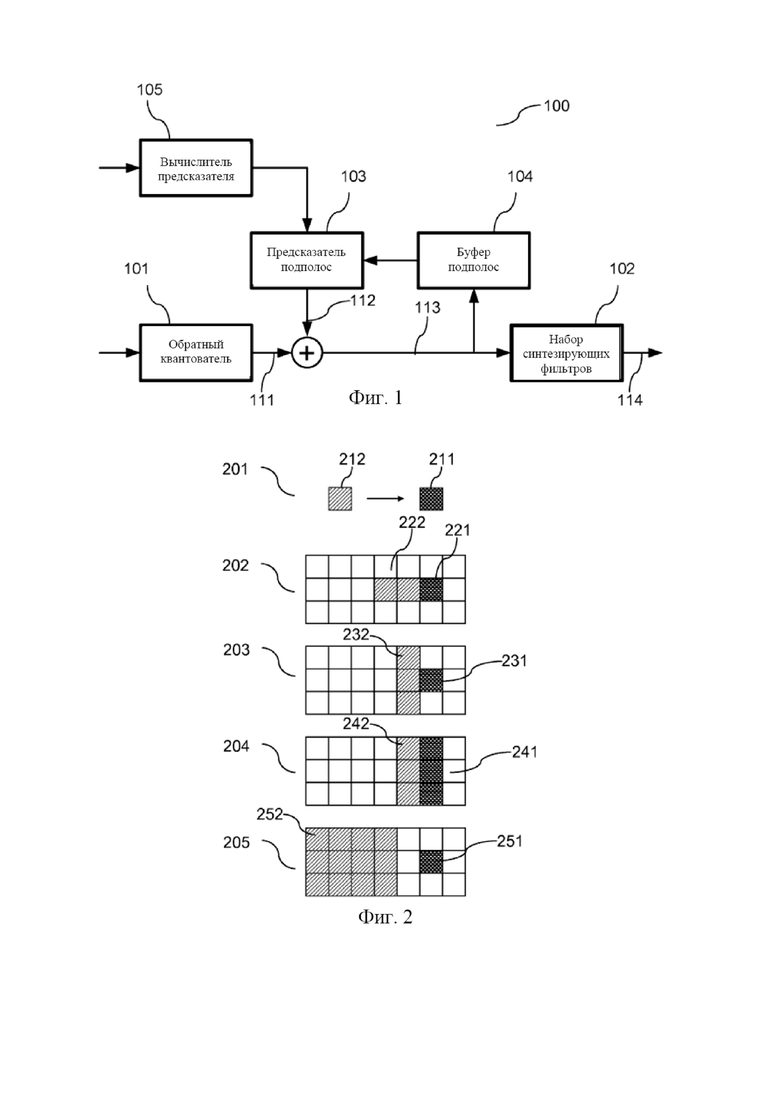
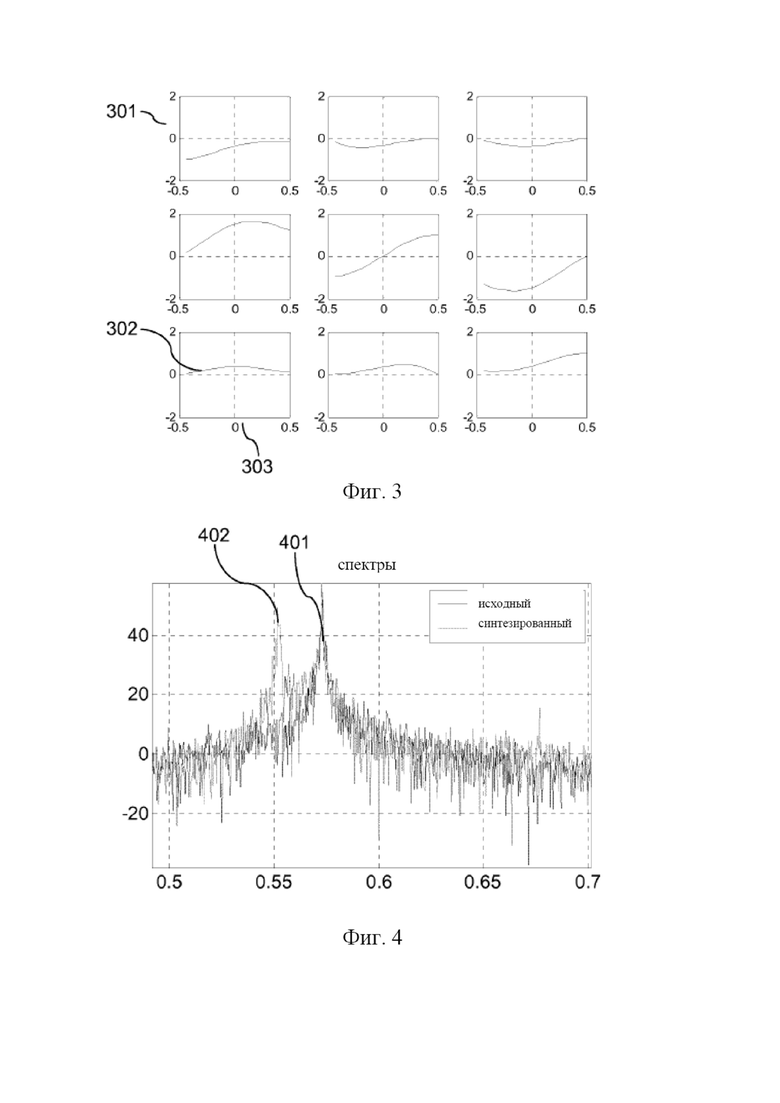
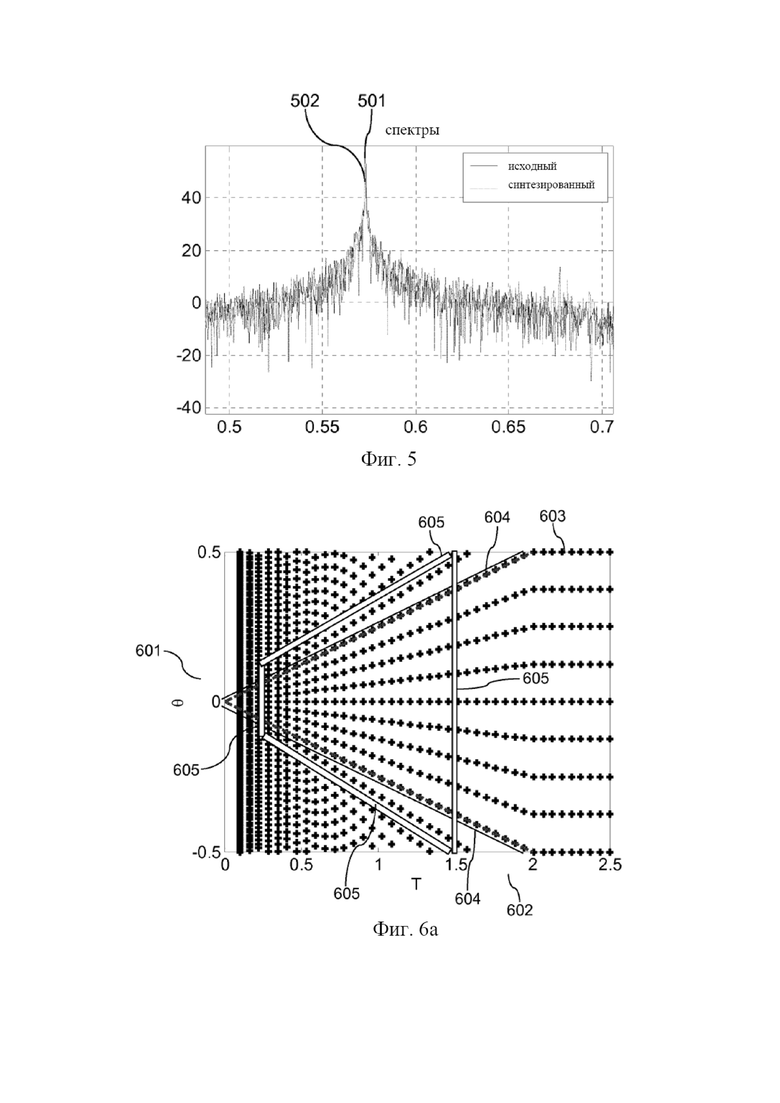
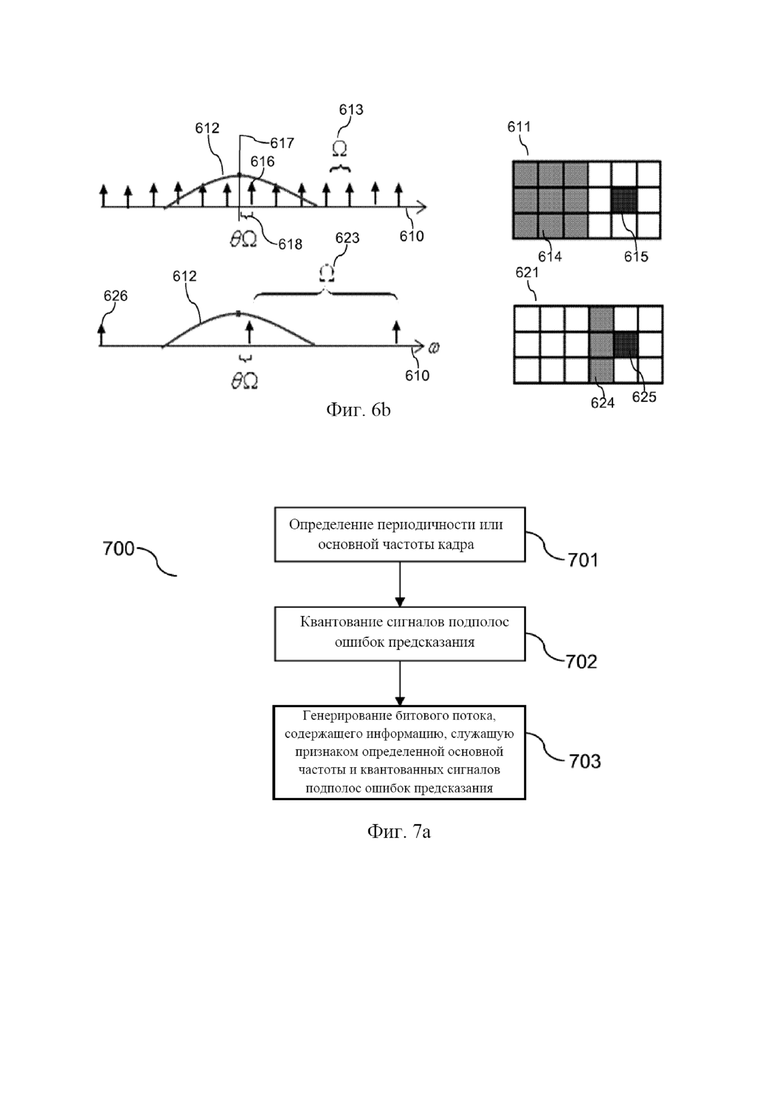
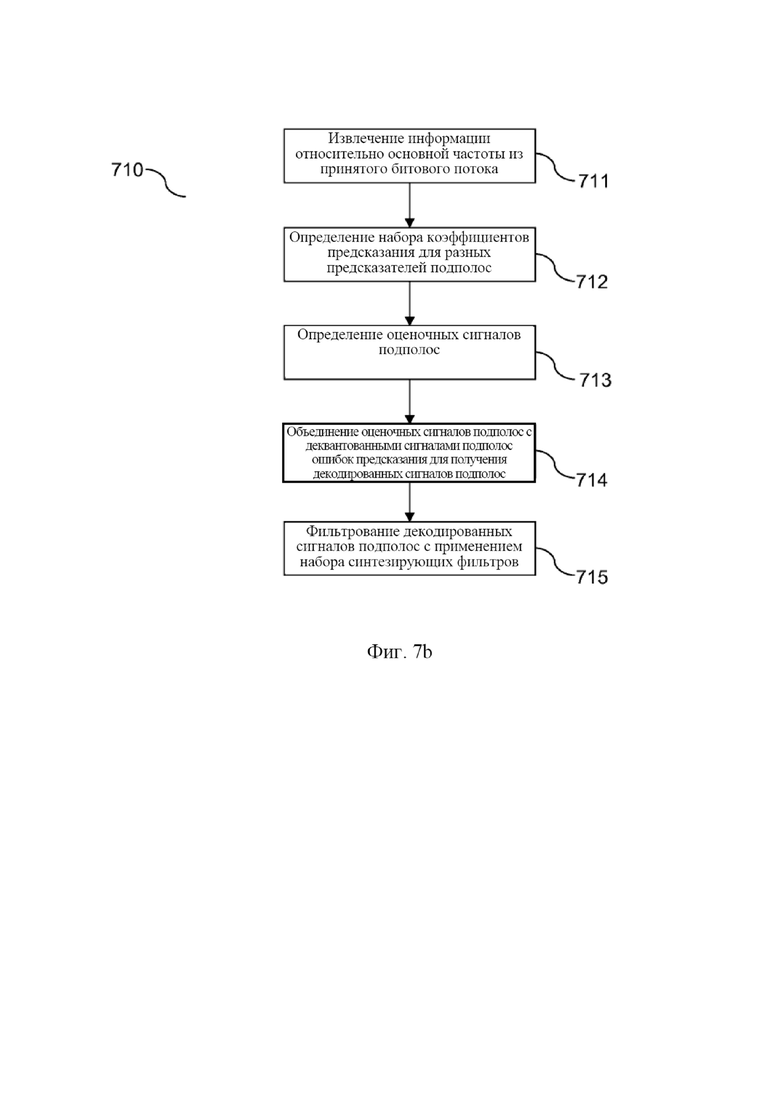
Изобретение относится к системам кодирования источника звука. Технический результат заключается в повышении эффективности кодирования. Определяют данные модели сигнала, содержащие параметр модели. Определяют первый коэффициент предсказания, подлежащий применению к первому предыдущему дискретному значению сигнала подполосы. Временной интервал первого предыдущего дискретного значения непосредственно предшествует временному интервалу первого дискретного значения. Первый коэффициент предсказания определяют в ответ на параметр модели с применением первой аналитической функции. Определяют второй коэффициент предсказания, подлежащий применению ко второму предыдущему дискретному значению сигнала подполосы. Временной интервал второго предыдущего дискретного значения непосредственно предшествует временному интервалу первого предыдущего дискретного значения. Второй коэффициент предсказания определяют в ответ на параметр модели с применением второй аналитической функции. Выполняют оценку дискретного значения посредством применения первого коэффициента предсказания к первому предыдущему дискретному значению и посредством применения второго коэффициента предсказания ко второму предыдущему дискретному значению. 3 н.п. ф-лы, 9 ил.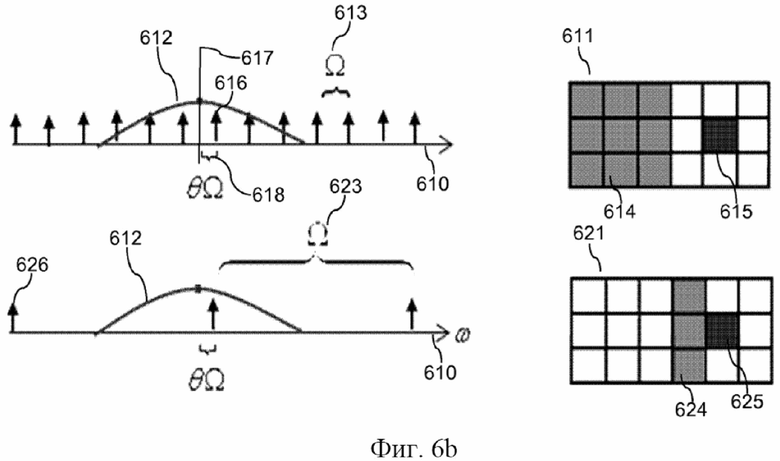
1. Способ оценки дискретного значения сигнала подполосы из двух или более предыдущих дискретных значений сигнала подполосы, выполняемый устройством обработки звуковых сигналов, при этом сигнал подполосы соответствует одной из множества подполос представления области подполос звукового сигнала, при этом способ включает:
определение данных модели сигнала, содержащих параметр модели;
определение первого коэффициента предсказания, подлежащего применению к первому предыдущему дискретному значению сигнала подполосы; при этом временной интервал первого предыдущего дискретного значения непосредственно предшествует временному интервалу первого дискретного значения; при этом первый коэффициент предсказания определяют в ответ на параметр модели с применением первой аналитической функции;
определение второго коэффициента предсказания, подлежащего применению ко второму предыдущему дискретному значению сигнала подполосы; при этом временной интервал второго предыдущего дискретного значения непосредственно предшествует временному интервалу первого предыдущего дискретного значения; при этом второй коэффициент предсказания определяют в ответ на параметр модели с применением второй аналитической функции; и
оценку дискретного значения посредством применения первого коэффициента предсказания к первому предыдущему дискретному значению и посредством применения второго коэффициента предсказания ко второму предыдущему дискретному значению;
при этом первая аналитическая функция и вторая аналитическая функция отличаются, и способ реализуют, по меньшей мере частично, посредством одного или нескольких процессоров устройства обработки звуковых сигналов.
2. Устройство обработки звуковых сигналов, выполненное с возможностью оценки дискретного значения сигнала подполосы из двух или более предыдущих дискретных значений сигнала подполосы, при этом сигнал подполосы соответствует одной из множества подполос представления области подполос звукового сигнала, при этом устройство обработки звуковых сигналов содержит:
вычислитель предсказателя, выполненный с возможностью:
определения данных модели сигнала, содержащих параметр модели;
определения первого коэффициента предсказания, подлежащего применению к первому предыдущему дискретному значению сигнала подполосы; при этом временной интервал первого предыдущего дискретного значения непосредственно предшествует временному интервалу первого дискретного значения; при этом первый коэффициент предсказания определяют в ответ на параметр модели с применением первой аналитической функции; и
определения второго коэффициента предсказания, подлежащего применению ко второму предыдущему дискретному значению сигнала подполосы; при этом временной интервал второго предыдущего дискретного значения непосредственно предшествует временному интервалу первого предыдущего дискретного значения; при этом второй коэффициент предсказания определяют в ответ на параметр модели с применением второй аналитической функции; и
предсказатель подполос, выполненный с возможностью оценки первого дискретного значения посредством применения первого коэффициента предсказания к первому предыдущему дискретному значению и посредством применения второго коэффициента предсказания ко второму предыдущему дискретному значению;
при этом первая аналитическая функция и вторая аналитическая функция отличаются, и один или несколько из вычислителя предсказателя и предсказателя подполос реализованы, по меньшей мере частично, посредством одного или нескольких процессоров устройства обработки звуковых сигналов.
3. Постоянный машиночитаемый носитель данных, содержащий последовательность команд, при осуществлении которых компьютер выполняет способ по п. 1.
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
| US 6633839 B2, 14.10.2003 | |||
| Способ приготовления лака | 1924 |
|
SU2011A1 |
| Способ приготовления лака | 1924 |
|
SU2011A1 |
| Способ приготовления лака | 1924 |
|
SU2011A1 |
| Колосоуборка | 1923 |
|
SU2009A1 |
| US 8055506 B2, 08.11.2011 | |||
| RU 2010152580 A, 27.06.2012 | |||
| АУДИОКОДИРОВАНИЕ С ИСПОЛЬЗОВАНИЕМ ПОНИЖАЮЩЕГО МИКШИРОВАНИЯ | 2008 |
|
RU2452043C2 |
Авторы
Даты
2024-06-11—Публикация
2020-12-18—Подача