Предлагаемый способ электронного контроля/реконструкции подверженной искажениям поверхности рефлектора крупногабаритной гибридной зеркальной антенны (ГЗА) относится к антенной технике, в первую очередь, к спутниковым многолучевым ГЗА, покрывающим рабочую область серией лучей. В условиях эксплуатационных нагрузок (из-за изменения теплового потока от Солнца при движении спутника по орбите) форма рефлектора ГЗА отклоняется от номинальной, что нарушает ориентацию лучей и снижает энергетический уровень покрытия рабочей зоны. Контроль текущего состояния отражающей поверхности рефлектора составляет основу (первый этап) процесса стабилизации лучей в этих условиях. Контроль поверхности рефлектора электронными средствами по сигналам, принимаемым от известного удаленного радио маяка, составляют перспективную альтернативу фотометрическим средствам контроля.
Известен предложенный Романовым П.В. способ электронного контроля (реконструкции) профиля рефлектора [P. Romanov, Multibeam antenna reflector distortions reconstruction via processing antenna array signals, 2020 7th All-Russian Microwave Conference (RMC), Moscow, Russia, 2020, pp.155-158; Романов П.В., Стабилизация лучей спутниковой многолучевой гибридной зеркальной антенны по сигналам антенной решетки при наличии шумов. «Вестник ПГТУ». Серия: радиотехнические и инфокоммуникационные системы. Выпуск 1, 2022 г. С. 6-20], который состоит в приеме сигналов от наземного маяка, выделении комплексных амплитуд {Sn} несущей этих сигналов, вычислении поля {Ер} в области около номинального рефлектора при возбуждении антенной решетки в соответствии с комплексно сопряженными сигналами {Sn*} и поиске точек, в которых фаза поля {Ер} совпадает с фазой плоской электромагнитной волны (ПЭМВ), распространяющейся в направлении на маяк. Недостаток способа состоит в большом объеме вычислений, реализующих циклы поискового алгоритма в отсутствии аналитического решения.
Прототипом заявляемого способа является способ контроля (реконструкции) профиля рефлектора, описанный в статье [Чони Ю.И., Романов П.В. Беспоисковый алгоритм реконструкции текущего профиля рефлектора гибридной зеркальной антенны по сигналам антенной решетки. «Антенны», №2 (276), 2022. С. 12-20]. Способ состоит в приеме сигналов от наземного маяка, расположенного по оптической оси номинального рефлектора, выделении комплексных амплитуд {Sn} несущей этих сигналов, вычислении поля {Ер} в точках номинального рефлектора при возбуждении антенной решетки в соответствии с комплексно сопряженными сигналами {Sn*}, и вычислении координат точек текущего профиля рефлектора путем смещения точек номинального рефлектора вдоль радиус-векторов от этих точек к фокусу соответствующего параболоида на отрезок Δrр=Δψр/k, где k=2π/λ есть волновое число, а Δψр=arg(Ep) - zp/k есть разность фаз полей Ер и ПЭМВ, распространяющейся на маяк. Недостаток прототипа заключается в необходимости вычислений в большом числе точек рефлектора, поскольку шаг между ними не должен превышать долей длины волны λ, чтобы было возможно избавиться от пилообразных скачков обратной тригонометрической функции arg(Ep) применением процедуры распаковывания (unwrapping), основанной на сопоставлении близких значений arg(Ep) в соседних точках. Поэтому число М расчетных точек рефлектора велико, и, несмотря на отсутствие поисковых циклов, объем вычислений не мал.
Целью предлагаемого способа является сокращение вычислительных затрат при контроле текущего профиля поверхности рефлектора. Решаемая техническая задача состоит в снижении нагрузки на процессор системы контроля, что имеет важное практическое значение, поскольку контроль профиля рефлектора осуществляется в реальном масштабе времени, как первый этап процесса управления ГЗА или стабилизации ее лучей.
Предлагаемый способ электронного контроля/реконструкции подверженной искажениям поверхности рефлектора крупногабаритной ГЗА заключается в облучении ГЗА, рефлектор которой в номинальном состоянии является параболоидом вращения с фокусным расстоянием Fr: zp=(хр2+yp2)/4Fr (р=0..М), узко полосным сигналом от удаленного источника с известными угловыми координатами (θоб, ϕоб), выделении комплексных амплитуд сигналов {Sn}, принятых элементами (n=1..N) антенной решетки (АР), вычислении комплексных амплитуд поля
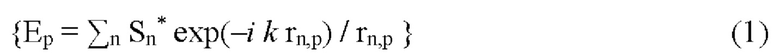
в точках номинального рефлектора, где астерик * означает комплексное сопряжение,k=2π/λ есть волновое число, a rn,p=((хр - xn)2+(ур - yn)2+(zp - zn)2)1/2 - расстояние между точками (xn, yn, zn) расположения элементов АР и расчетными точками (хр, ур, zp) поверхности рефлектора, технический результат достигается тем, что поле {Ер} пересчитывается в поле {Up} на апертурной плоскости Р, перпендикулярной направлению (θоб, ϕоб), по правилу
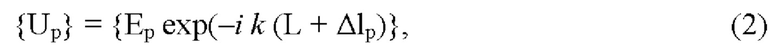
где Δlp=(хр sinθaosϕ+урsinθsinϕ+zpcosθ) - расстояние между точками (хр, ур, zp) рефлектора и плоскостью, проходящей через начало системы координат перпендикулярно направлению (θоб, ϕоб), L - расстояние апертурной плоскости Р от начала системы координат. Затем среди точек рефлектора (р=0..М) выбирают точку р', не подверженную смещениям, вычисляют разности фаз Δψр=arg(Up / UP') и определяют координаты точек (хр'; ур', zp') текущего профиля рефлектора по формулам: Δlр=Δψр/k(1+(xpcos(ϕоб)sin(θоб)+yPsin(ϕоб)sin(θоб)+(Fr-zp)cos(θоб))/ρP),
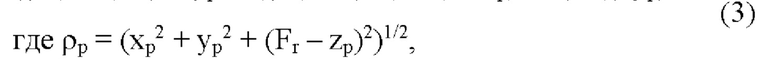
хр'=хр+Δlp cos(ϕоб) sin(θоб),
yp'=yP+Δlр sin(ϕоб) sin(θоб),
zp'=zp+Δlp cos(θоб),
смысл которых состоит в смещении точки номинального рефлектора на отрезок Δlp по лучу (θоб, ϕоб), причем значение Δlр обеспечивает компенсацию разность фаз Δψр за счет изменения расстояния до апертурной плоскости Р с учетом сдвига фазы поля сферической волны Ер от АР.
И по физическому смыслу (и формально!) разность фаз Δψр=arg(Up/UP') не зависит от расстояния L, и его значение можно принято любым, включая абстрактное L=0.
В отличие от прототипа фазовую структуру поля Ер сопоставляют с фазовым фронтом ПЭМВ не в точках рефлектора, где эти фазы резко изменяются в диапазоне в десятки раз превышающем 2π, а в точках апертурой плоскости Р, на которой поле ПЭМВ синфазно, а фаза поля Up, формирующего максимум в направлении (θоб, ψоб), близка к синфазному распределению. Поэтому проблема со скачками функции arg(Up), как минимум, существенно ослабляется, и сетка расчетных точек рефлектора (р=0..М) может быть разрежена до ячеек размером в несколько длин волн, что существенно снижает число точек М и объем вычислений.
Дополнительный технический результат состоит в уменьшении числа элементов измерительного кластера (элементов антенной решетки, используемых в вычислениях по реконструкции текущего профиля рефлектора), который достигается за счет того, что измеренные сигналы {Sn} сравнивают по амплитуде с некоторым пороговым сигналом Ао и в состав измерительного кластера включают элементы АР, удовлетворяющие условию |Sn|>Ао, и последующую обработку сигналов {Sn*} по формуле (1) осуществляют суммированием только по выделенным элементам, причем уровень сигнала Ао определяют из условия перехвата измерительным кластером существенной доли принимаемой АР мощности Σn |Sn|2, при которой обеспечивается приемлемая точность реконструкции.
3. Способ по п. 2, отличающийся тем, что в качестве выделенной области АР используют номинальный кластер, формирующий луч в направлении (θоб, ψоб).
В условиях априори малых искажений профиля рефлектора выделенной областью АР может служить группа элементов номинального кластера, формирующего луч в направлении (θоб, ψоб).
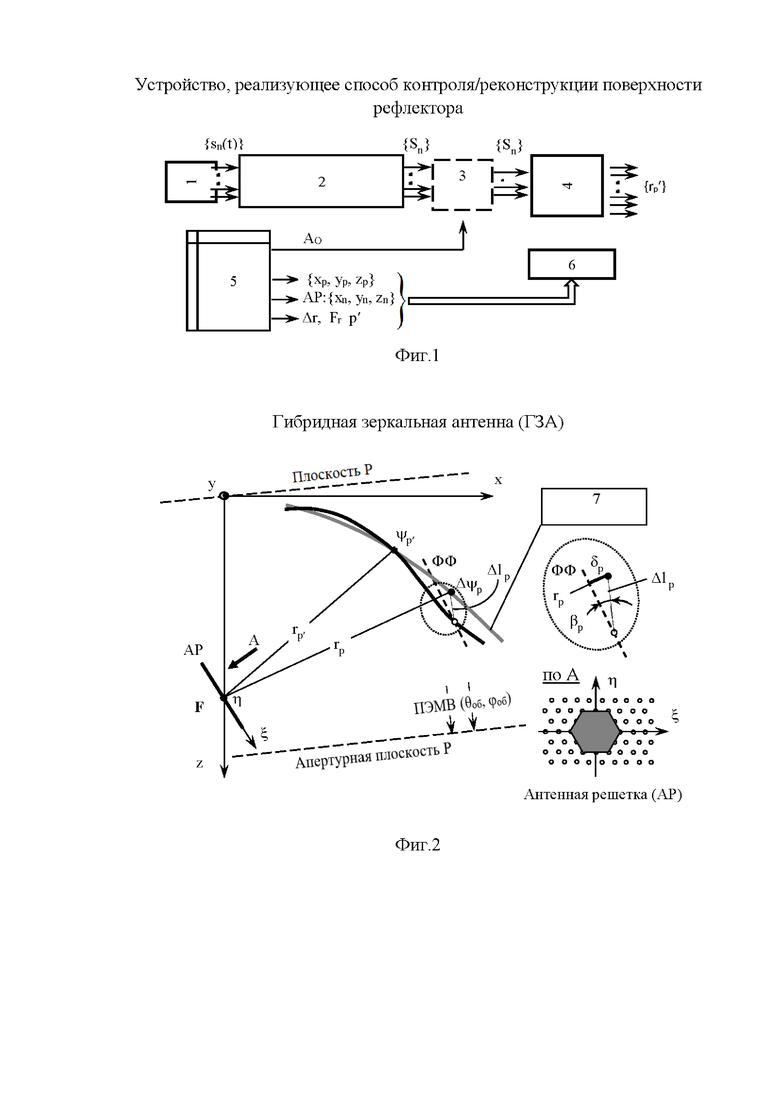
На фиг. 1 представлена структура устройства, реализующего заявляемый способ электронного контроля/реконструкции поверхности рефлектора ГЗА, где 1 - ГЗА, 2 - N-канальный цифровой приемник, 3 - Селектор каналов |Sn|>Ао, 4 - Расчет полей {Ер}, {Up},смещений Δ1р и и, 5 - исходные данные, 6 - процессор.
На фиг. 2 представлена типичная геометрия спутниковой ГЗА, система координат и размеры, которые использовались при компьютерном моделировании результатов контроля профиля рефлектора ГЗА по заявляемому способу. Здесь 7 - номинальный рефлектор.
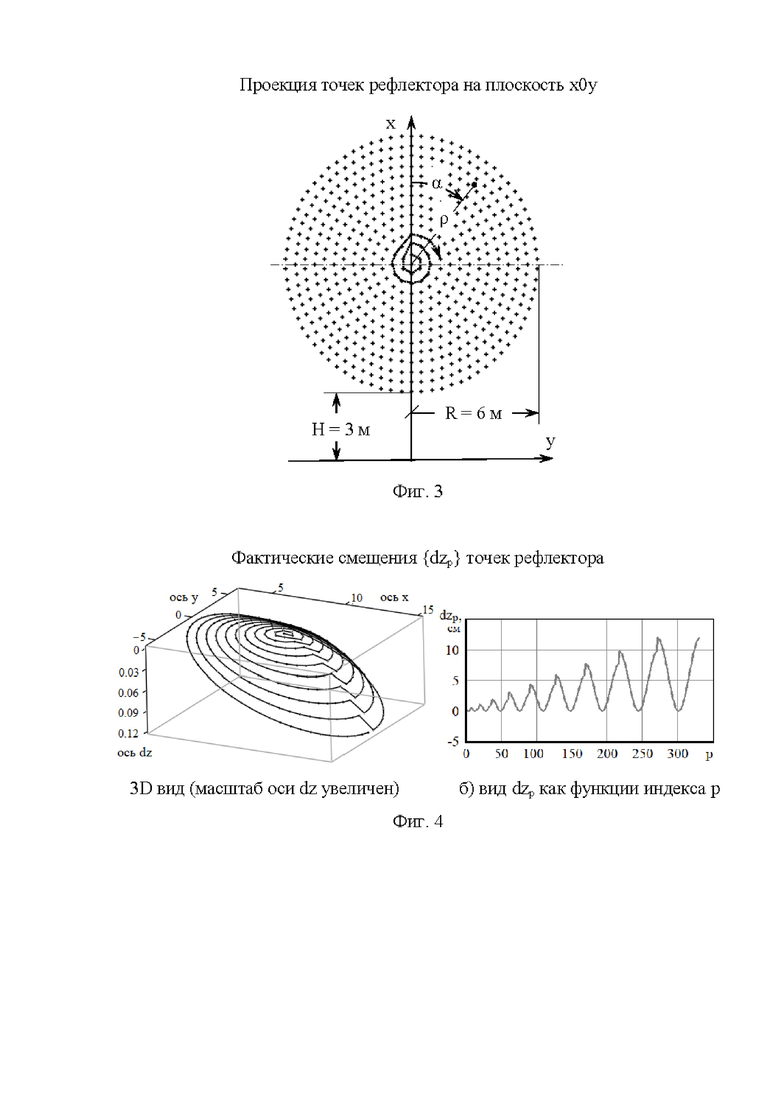
Фиг. 3 иллюстрирует расположение расчетных точек в проекции на плоскость х0у и порядок их обхода при росте индекса р (от 0 до М=330).
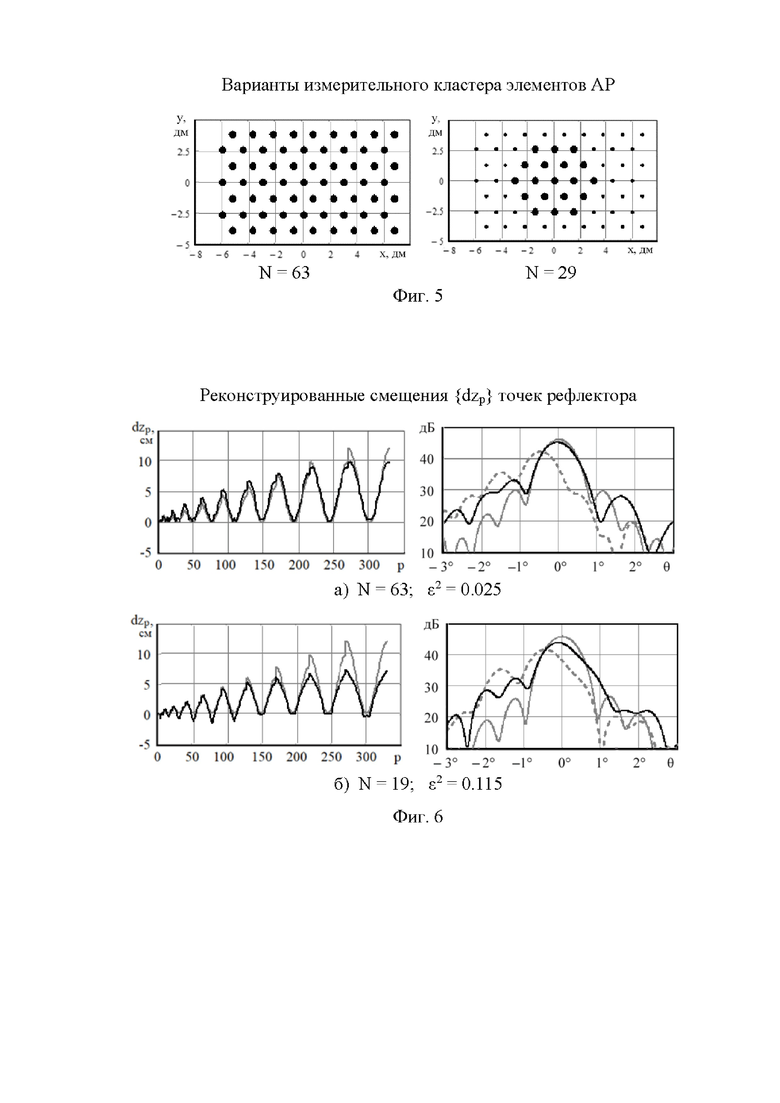
На фиг. 4 изображены фактические смещения {dzp} точек рефлектора при моделируемых искажениях рефлектора в виде 3D поверхности и в виде зависимости от индекса р точек.
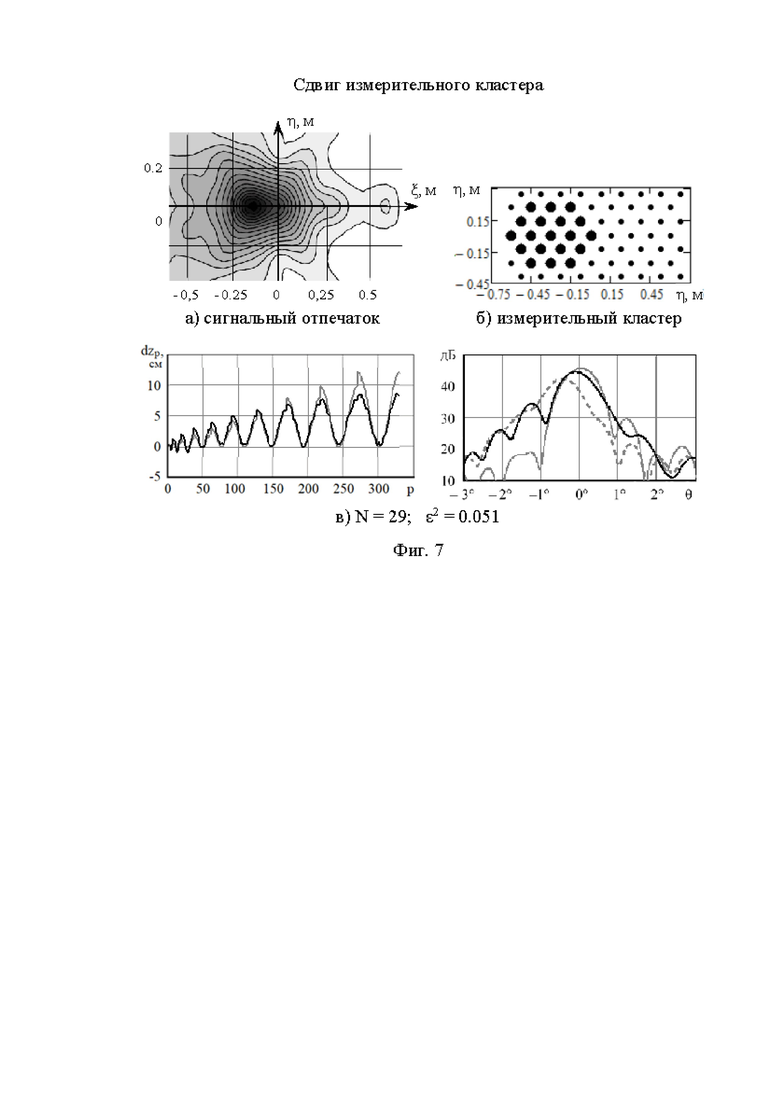
На фиг. 5 представлены конфигурации двух вариантов измерительного кластера элементов АР.
Фигура 6 иллюстрирует точность реконструкции профиля рефлектора и стабилизации центрального луча ГЗА.
На фиг. 7 представлены результаты моделирования при адаптации измерительного кластера по сигнальному отпечатку на АР.
Рассмотрим осуществление заявляемого способа электронного контроля/реконструкции подверженной искажениям поверхности рефлектора крупногабаритной гибридной зеркальной антенны (ГЗА). Для конкретности, на примере многолучевой ГЗА геостационарного спутника с осью рефлектора, ориентированной на наземный облучающий радиомаяк (θоб=0, ψоб=0).
На фиг. 1 представлена укрупненная структурная схема устройства, реализующего заявляемый способ. Сигналы {sn(t)} от АР поступают в N-канальный цифровой приемник [описание доступно по ссылке https://dic.academic.ra/dic.nsf/ruwiki/1188771#], осуществляющий когерентный прием сигналов, фильтрацию и оцифровку комплексных амплитуд {Sn} их несущих. Процессор реализует вычисления в соответствии с выше приведенными формулами (1), (2) и (3). Реконструированные координаты {rр'} точек рефлектора в текущем состоянии используются системой стабилизации лучей ГЗА или управления ею. Блок селектора каналов, выделенный пунктиром на структурной схеме, реализует функции, указанные в п. 2 формулы изобретения, и может отсутствовать, если состав измерительного кластера фиксирован и не адаптируется в реальном времени к текущей ситуации.
На фиг.2 представлены типичная геометрия ГЗА, построенной по оптической схеме с вынесенным фокусом, что исключает затенение апертуры ГЗА конструкцией АР. Кроме того, поясняются геометрические и физические факторы, стоящие за формулами (3). Для этого выделена малая эллиптическая область вблизи конкретной точки р номинального рефлектора, обозначенная жирной черной точкой. Точка, обозначенная окружностью, смещена к апертурной плоскости Р на отрезок Δ1р в направлении (θоб, ψоб). Пусть Δψр=arg(Up/Up`) - разность фаз в точках плоскости Р, соответствующих индексам р и р'. Смещение точки р на Δ1Р к апертуре Р вызывает опережение фазы на k Δ1р за счет сокращения дистанции до апертуры плюс дополнительное опережение фазы на k δР за счет сокращения расстояния, проходимого сферической волной поля Ер. На фиг. 2 в увеличенном эллипсе справа соответствующий отрезок выделен жирной линией. Очевидно, что δР=Δ1р cos(π/2 - βр), и косинус, как скалярное произведение вектора Δ1р и орта ρР/|ρр|, определяются формулой
(xpcos(ψоб) sin(θоб)+УР sin(ψоб) sin(θo6)+(Fr-zp) cos(θоб))/ρP,
где ρр=(хр2+ур2+(Fr - zp)2)1/2
Приравнивая Δψр и k Δ1р (1+cos(π/2 - (βр), получаем формулы (3) для смещения Δ1р и для точек хр', ур', zp' реконструированного рефлектора. В основе предлагаемого способа лежат следующие факты.
1) Спутниковые многолучевые ГЗА имеют габариты порядка сотни и более длин волн, строятся по длиннофокусной (кривизна рефлектора не велика) офсетной схеме (АР не затеняет апертуру ГЗА) и формируют лучи в ограниченном телесном угле (в пределах ±8°) около оптической оси рефлектора. Поэтому краевые эффекты и деполяризация поля пренебрежимо малы. Методы геометрической оптики в скалярном (акустическом) варианте корректно отражает физику процессов подобных ГЗА [Мочалов, В.В. «Аттестация алгоритма акустической аппроксимации», Телекоммуникации и радиотехника, 2019, т.73, №12. С.122-126, DOI: 10.18127 / j20700784-201912-19]. Тем более, что реальные эксплуатационные искажения поверхности рефлектора относительно малы и гладки.
2) Известный [Сазонов Д.М., Антенны и устройства СВЧ: учеб. для радиотехнич. спец. вузов - М. высш. шк., 1988, формула (13.27) на стр. 357] и понятный по физическим соображениям принцип формирования максимума КНД (синфазное сложение полей излучателей) в желаемом направлении (θоб, ψоб) сводится к возбуждению АР в соответствии с комплексно сопряженными значениями вторичных (в присутствии рефлектора) ДН fn(θ, ϕ) элементов АР в направлении (θоб, ψоб)- Очевидно, что сигналы {Sn}, принимаемые элементами АР от маяка, пропорциональны значениями ДН {Sn~ fn(θоб, ψоб)}- Поэтому возбуждение АР в соответствии с комплексно сопряженными сигналами {Sn*} обеспечивает максимум КНД в направлении на маяк.
3) С другой стороны, максимум КНД в направлении (θоб, ψоб) соответствует синфазному полю в апертуре.
Таким образом, рефлектор при текущем его состоянии трансформирует фазовый фронт поля от АР, возбужденной в соответствии с сигналами Sn*, в участок ПЭМВ на апертуре ГЗА, и суть заявляемого способа состоит в вычислении точек текущего профиля рефлектора за счет таких смещений точек номинального рефлектора, при которых фазовая структура поля {Ер} преобразуется в синфазный фронт {Up} на апертурной плоскости.
Преимущества предлагаемого способа по сравнению с прототипом проявляются в значительном сокращении объема вычислений и, соответственно, нагрузки на процессор, осуществляющий эти вычисления. В частности, для беспоискового алгоритма реконструкции профиля рефлектора по прототипу [Чони Ю.И., Романов П.В. Беспоисковый алгоритм реконструкции текущего профиля рефлектора гибридной зеркальной антенны по сигналам антенной решетки. «Антенны», №2 (276), 2022. С. 12-20, стр. 15 в конце первого абзаца под рис. 2] необходим «отмеченным выше порядком расположения точек на все возрастающих окружностях при шаге радиусов в λ/2 и дискрете ≈λ/2 точек на них» (конец цитаты). При диаметре рефлектора 80 λ требуемое число точек для прототипа составляет М=19 440.
Представленные ниже на фиг. 3-7 результаты моделирования заявляемого способа подтверждают его работоспособность при шаге сетки точек рефлектора Δr=4λ, что соответствует их числу М=330 в 60 раз меньше требуемого по прототипу. Кстати, значение М=330 в полной мере согласуется с оценкой минимально приемлемого значения М=250, указанного в конце левой колонки на стр. 72 статьи [Калабегашвили Г.И., Бикеев Е.В., Матыленко М.Г. Поиск минимального количества точек отражающей поверхности рефлектора, необходимого для оценки отклонения диаграммы направленности крупногабаритных трансформируемых антенн. Сибирский журнал науки и технологий. 2018. Т. 19, №1. С. 66-75. Доступно по ссылке https://vestnik.sibsau.ru/vestnik/862/].
Расчетные точки рефлектора (хр, ур, zp) в проекции на плоскость х0у (фиг. 3) образуют концентрические окружности с дискретом 4λ, и расположены на них равномерно с шагом около АХ. Ось z направлена по оптической оси. В номинальном состоянии рефлектор является параболоидом вращения с фокусным расстоянием Fr=7.4 м: z(x, у)=(х2+y2)/4Fr. При длине волны λ=15 см (рабочая частота 2Ггц) число М=330. Центральная точка рефлектора нумеруется как р=0, и рост индекса р соответствует обходу точек по окружности с перескоком на соседнюю, как показано на фиг. 3 (интервала р=0..24). Принято, что направление облучения соответствует оптической оси (θоб=0, ψоб=0).
Моделировались искажения профиля рефлектора в виде изменений координаты z, z'(x, у)=z(x, у)+dz при dz(x, у)=0.4 λ, (1+cos(α)) (ρ/R)2, где (ρ, α) - полярные координаты точек (х, у). Это соответствует отклонениям точек рефлектора в виде «козырька» с максимумом в 12 см в верхней точке рефлектора (х=Н+R, у=0). На фиг. 4а показан 3D-вид искажений dz(x, у), причем в интересах наглядности, масштаб по оси dz изменен на 2 порядка по сравнению с масштабами осей х и у. На фиг.4б представлены те же искажения dzp=dz(xp, ур) в зависимости от индекса р. Осциллирующий характер этой зависимости соответствует траектории перемещения точки по рефлектору: по окружностям с перескоком на соседнюю (фиг. 3).
Моделировались два варианта измерительных кластеров, представленных на фиг. 5: а) АР габаритов 1.45 м на 1 м, 63 элементы которой расположены в узлах гексагональной сетки с ячейками в 15 см; б) кластер из 19-ти элементов.
Результаты моделирования представлены на фиг. 6, где черными кривыми на правых рисунках показаны реконструированные смещения точек рефлектора, а серыми - фактические смещения (повторяют соответствующую зависимость на фиг. 5). В подрисуночных подписях приведены значения СКО ε2=Σр |2р'факт - Zp'peк|2/Σp |Zp |2р'факт |2, характеризующие точность реконструкции. Естественно, точность тем выше, чем больше габариты измерительного кластера. Слева на фиг. 6 представлены диаграммы направленности (ДН), формируемые тем же кластером, который используется при контроле/реконструкции поверхности рефлектора. Здесь и в дальнейшем серыми сплошными линиями представлен луч номинального рефлектора с максимумом в направлении (θоб=0, ψоб=0), серой пунктирными линигми - луч искаженного рефлектора при сохранении амплитудно-фазового распределения номинального рефлектора; черными линиями - луч искаженного рефлектора при амплитудно-фазовом распределении кластера, скорректированном по результатам реконструкции.
В соответствии с п. 2 предлагаемого способа контроля/реконструкции поверхности рефлектора ГЗА, положение и состав измерительного кластера выбираются такими, чтобы перехватывать большую часть принимаемой АР мощности. На фиг. 7 приведены результаты моделирования подобного подхода. При козырьковом, как описано выше, искажении рефлектора имеет место сигнальный отпечаток (амплитудный рельеф сигналов АР {|Sn|}), представлен на фиг. 7а линиями уровней. Измерительный кластер из 19-ти элементов сдвинут из центра АР вслед за максимумом сигнального отпечатка. При этом точность реконструкции искажений поверхности рефлектора и качество стабилизированного луча возрастают, как показано на графиках фиг. 7в. Эти результаты подтверждают дополнительный технический эффект представлены, который состоит в повышении точности реконструкции при сохранении числа элементов измерительного кластера или в уменьшении числа элементов кластера при той же точности реконструкции.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ стабилизации лучей спутниковой гибридной зеркальной антенной по сигналам наземного радиомаяка | 2023 |
|
RU2826368C1 |
| Способ стабилизации лучей спутниковой многолучевой гибридной зеркальной антенны по сигналам от смещенных наземных маяков | 2019 |
|
RU2727860C1 |
| ГИБРИДНАЯ ЗЕРКАЛЬНАЯ АНТЕННА С РАСШИРЕННЫМИ УГЛАМИ СЕКТОРНОГО СКАНИРОВАНИЯ | 2007 |
|
RU2352033C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ РАДИОТЕХНИЧЕСКИХ ХАРАКТЕРИСТИК КРУПНОГАБАРИТНЫХ АНТЕНН ДЛЯ КОСМИЧЕСКИХ АППАРАТОВ БЕЗ ИХ НЕПОСРЕДСТВЕННЫХ ИЗМЕРЕНИЙ | 2013 |
|
RU2541206C2 |
| СКАНИРУЮЩАЯ ГИБРИДНАЯ ЗЕРКАЛЬНАЯ АНТЕННА | 2009 |
|
RU2392703C1 |
| СПОСОБ ФОРМИРОВАНИЯ КЛАСТЕРНЫХ ЗОН ОБЛУЧАЮЩЕЙ РЕШЕТКОЙ МНОГОЛУЧЕВОЙ ГИБРИДНОЙ ЗЕРКАЛЬНОЙ АНТЕННЫ | 2014 |
|
RU2578289C1 |
| Способ фокусирования поля N-элементной антенной решетки | 2024 |
|
RU2828163C1 |
| Гибридная зеркальная антенна кругового обзора | 2024 |
|
RU2821244C1 |
| Устройство для задания конфигурации области | 1978 |
|
SU752382A1 |
| МНОГОЛУЧЕВАЯ НЕАПЛАНАТИЧЕСКАЯ ГИБРИДНАЯ ЗЕРКАЛЬНАЯ АНТЕННА | 2001 |
|
RU2181519C1 |
Изобретение относится к антенной технике, в частности к спутниковым многолучевым гибридным зеркальным антеннам (ГЗА), и представляет собой способ контроля-реконструкции подверженной искажениям поверхности рефлектора крупногабаритной ГЗА. Технический результат - снижение нагрузки на процессор системы контроля. Результат достигается тем, что предложен способ контроля-реконструкции подверженной искажениям поверхности рефлектора крупногабаритной гибридной зеркальной антенны (ГЗА), включающий облучение ГЗА, рефлектор которой в номинальном состоянии является параболоидом вращения, узкополосным сигналом от удаленного источника с известными угловыми координатами, выделение комплексных амплитуд сигналов, принятых элементами антенной решетки (АР), вычисление комплексных амплитуд поля в точках номинального рефлектора, отличающийся тем, что поле в точках номинального рефлектора пересчитывается в поле на апертурной плоскости, перпендикулярной направлению удаленного источника с известными угловыми координатами. 2 з.п. ф-лы, 7 ил.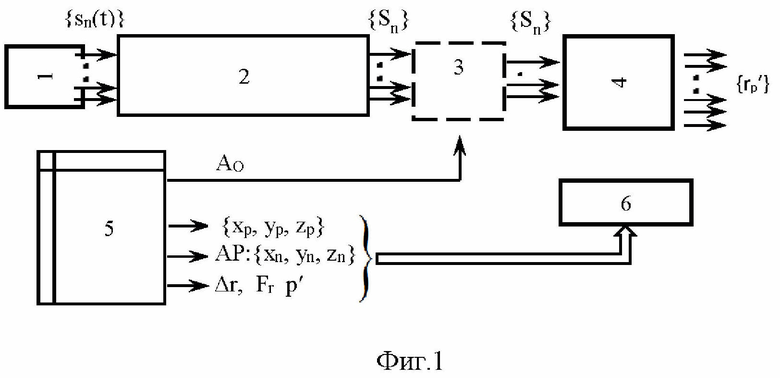
1. Способ контроля-реконструкции подверженной искажениям поверхности рефлектора крупногабаритной гибридной зеркальной антенны (ГЗА), включающий облучение ГЗА, рефлектор которой в номинальном состоянии является параболоидом вращения zp=(хр2+yp2)/4Fp (р=0..М), узкополосным сигналом от удаленного источника с известными угловыми координатами (θоб, ϕоб), выделение комплексных амплитуд сигналов {Sn}, принятых элементами (n=1..N) антенной решетки (АР), вычисление комплексных амплитуд поля
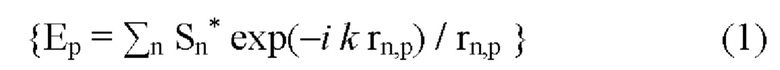
в точках номинального рефлектора, где астерик * означает комплексное сопряжение, k=2π/λ есть волновое число, а rn,р - расстояние между точками (xn, yn, zn) расположения элементов АР и точками (хр, ур, zp) на поверхности рефлектора, отличающийся тем, что поле {Ер} пересчитывается в поле {Up} на апертурной плоскости Р, перпендикулярной направлению (θоб, ϕоб), по правилу
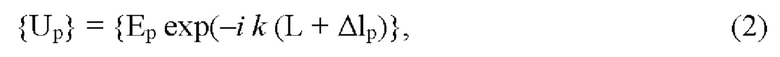
где Δ1р=(хр sinθ cosϕ + ур sinθ sinϕ + zp cosθ) - длина лучей между точками (хр, ур, zp) рефлектора и плоскостью, проходящей через начало системы координат перпендикулярно направлению (θоб, ϕоб), L - расстояние апертурной плоскости Р от начала системы координат, затем среди точек рефлектора (р=1..М) выбирают точку р', не подверженную смещениям, вычисляют разности фаз Δψр=arg(Up/UP') и определяют координаты точек (хр'; ур', zp') искаженного рефлектора по правилу:
Δ1р=Δψр/k(1+(xpcos(ϕоб)sin(θоб)+yPsin(ϕоб)sin(θоб)+(Fr-zp)cos(θоб))/ρp)
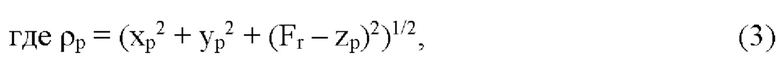
хр'=хр+Δ1p cos(ϕоб) sin(θоб),
ур'=ур+Δ1p sin(ϕоб) sin(θоб),
zp'=zp+Δ1p cos(θоб).
2. Способ по п. l, отличающийся тем, что измеренные сигналы {Sn} сравнивают по амплитуде с некоторым пороговым сигналом А0 и в состав измерительного кластера включают элементы АР, удовлетворяющие условию |Sn|>Ао, и последующую обработку сигналов {Sn*} по формуле (1) осуществляют суммированием только по выделенным элементам, причем уровень сигнала А0 определяют из условия перехвата измерительным кластером существенной доли принимаемой АР мощности Σn |Sn|2, при которой обеспечивается приемлемая точность реконструкции.
3. Способ по п. 2, отличающийся тем, что в качестве выделенной области АР используют номинальный кластер, формирующий луч в направлении (θоб, ϕоб).
| Чони Ю.И., Романов П.В | |||
| Беспоисковый алгоритм реконструкции текущего профиля рефлектора гибридной зеркальной антенны по сигналам антенной решетки, Журнал "Антенны", N2 (276), 2022, стр | |||
| Способ гальванического снятия позолоты с серебряных изделий без заметного изменения их формы | 1923 |
|
SU12A1 |
| Романов П.В., Чони Ю.И | |||
| Реконструкция профиля рефлектора спутниковой многолучевой гибридной зеркальной антенны путем обработки сигнала наземного маяка, | |||
Авторы
Даты
2024-07-23—Публикация
2023-12-09—Подача