Область техники, к которой относится изобретение
Предлагаемое в качестве изобретения техническое решение относится к методам обработки данных, используемых для построения систем, позволяющих решать задачи распознавание образов, классификации и количественного содержания целевого параметра (регрессии), на основе измерений, представляющих из себя непрерывные одномерные сигналы.
В частности, изобретение может быть использовано для определения газов и их концентрации на основе сигналов, например, с полупроводниковых сенсоров; определения типов неорганических соединений и их концентраций в растворах на основе методов спектроскопии; и др.
Уровень техники
Обработка многомерных векторных сигналов является общей задачей анализа данных, которая в свою очередь может сводиться к распознаванию образов для определения количественного значения целевого параметра, предсказания его будущих значений или определения его принадлежности к той или иной целевой группе. Для устойчивого решения поставленной задачи в рамках парадигмы моделей машинного обучения необходимо подобрать значения коэффициентов модели машинного обучения после проведения процедуры обучения на массиве примеров релевантных задаче (обучающей выборке), итеративно подаваемых модели и корректировки обучаемых коэффициентов на основе ответов модели.
Простой иллюстрацией такого подхода является метод ближайшего соседа (US 2013/0197384 A1), определяющий количественные характеристики и принадлежность примера к классу на основе непосредственной схожести поступившего сигнала с сигналом из обучающей выборки. Однако такой подход не позволяет проследить зависимости внутри данных и получить их численное описание, с чем легко справляются классические линейные регрессионные модели (US 007142105 B2, US 2016/0132617 A1), результатом которых является подбор коэффициентов для параметров векторных сигналов исходной размерности, линейная комбинация которых соответствует целевому значению.
Развитием данного подхода является отображение пространства входных примеров в пространство меньшей размерности для более устойчивой аппроксимации значений примеров. Наиболее распространенным методом, реализующим данную концепцию, является метод главных компонент, который может быть использован для определения типов газов в смеси на основе координат обработанных примеров в пространстве главных компонент (ЕР 3619526). Слабой стороной данного метода является построение отображения в пространство низкой размерности на основе статистических характеристик измеряемых признаков, без учета целевых показателей (в данном примере типов газов), соответствующих измерения.
Данного недостатка лишена модель частичных наименьших квадратов (US 2006/0155486), являющаяся модификацией метода главных компонент, но использующая совместно матрицы входных векторных сигналов (показаний полупроводниковых сенсоров на протяжении временных интервалов с заданным изменением температуры) и желаемых значений (типов газов) для построения системы координат меньшей размерности. Авторы отмечают недостатки представленных линейных моделей машинного обучения и предполагают проведение процедур предобработки, на основе простых математических операций вроде логарифмирования, потенцирования и пр. для описания нелинейных зависимостей в данных.
Более общим методом обработки данных с нелинейными зависимостями является использование нейронных сетей, использующую метод обратного распространения ошибки, обеспечивающий высокую точность и согласованность результатов, например, для задачи диагностики заболеваний по измерениям выдыхаемого воздуха (IN 202211021394) или загрязнения воздуха окружающей среды опасными компонентами (US 2016/0125307 A1).
Недостатком известных технических решений является избыточность числа параметров модели нейронной сети при работе с задачами обработки измерений реальных приборов, поскольку нейронная сеть требует огромного числа примеров обучающей выборки, в противном случае может наблюдаться эффект переобучения, в рамках которого нейронная сеть выучивает все примеры обучающей выборки, но практически полностью теряет способность к устойчивому решению задачи. В связи с эти эффективное применение нейронные сети в основном находят в задачах с огромным количеством измерений, например, обработке сигналов биоэлектрической активности, записанной с помощью ЭЭГ и МЭГ (US 8725669 B1), либо в задачах анализа данных сети интернет и сетевого траффика в частности (US 20200387797 A1). Такие объемы данных позволяют обучать нейронные сети в составе комплексов генеративные состязательных сетей в рамках парадигмы «обучения без учителя» (US 10956808 B1), что существенно упрощает подготовку данных, поскольку не требует подготовки набора целевых показателей, соответствующих обрабатываемым входным примерам. Обратной стороной является сложность обучения нейронных сетей и требование к объему и представительности обучающей выборки, ведь статистическая природа обучения нейросетевой модели означает низкую уверенность ответов модели для так называемых примеров-выбросов, т.е. примеров чьи значения находятся на границах или за пределами распределения примеров обучающей выборки.
Наиболее простым подходом к работе с такими примерами является расчет классических статистических оценок, например, анализом набора статистических показателей данных измеряющих сенсоров (US 20220019863). Использование классических статистических тестов затруднительно при работе с многомерными векторными сигналами, в связи с чем для работы с векторными сигналами высокой размерности используется оценка расстояния в пространстве векторных сигналов от заранее вычисленного центроида групп данных, например, расстояние Махаланобиса (US 20200025700) или Евклидова расстояния для минорных кластеров модели К-средних (US 10318886 B2). Как было упомянуто ранее, более эффективным является переход к низкоразмерному отображению исходных примеров, например, в пространство главных компонент (US 8850608 B2), на основе амплитуды координат которых можно сделать вывод о том, является ли векторный сигнал выбросом или нет. Развитием данного подхода является анализ отображений примеров в глубоких слоях нейронной сети (US 20210350113 A1) и последующим сравнением такого отображения нового векторного примера с примерами обучающей выборки нейронной сети. Данное сравнение может проводится, как с помощью дополнительной модели машинного обучения, например, метода проекционной регрессии преследования (ЕР 3652596), так и на основе ансамбля схожих нейросетевых моделей (US 20030191728 A1) обучавшихся на данных с разными статистическими свойствами (например, использовались различные параметры добавления шума). Основной претензией к ансамблевым подходам является увеличение времени вычислений (WO 2022036441), которые потребуются для решения данной задачи, поскольку в ходе его реализации потребуется подобрать параметры для множества моделей машинного обучения, обучаемых на множестве наборов данных
Наиболее близким к заявляемому техническому решению является способ и система для анализа сигналов, представленного в векторной форме, для распознавания образов (US 11593650 B2). Способ включает создание тренировочного массива данных и трансформацию признаков этого массива в стандартное представление; обучение модели машинного обучения для определения примеров-выбросов в рамках решения задачи классификации; распознавание образов на основе глубокой нейронной сети для примеров, прошедших процедуру фильтрации.
Раскрытие сущности изобретения
Задачей настоящего изобретения является создание способа обработки данных векторных сигналов для распознавания образов на основе методов полиномиальной аппроксимации, частичных наименьших квадратов и нейронных сетей - такой комплекс методов обработки исходного сигнала снижает влияние артефактов, наблюдаемых при изменении условий среды и смене температурного режима сенсора, что повышает устойчивость решения задачи определения целевого параметра (концентрации водорода).
Техническим результатом изобретения является возможность количественного определения целевого параметра, устойчивого к присутствию шумовых эффектов в оригинальном измерении.
Поставленная задача решается обработкой векторных сигналов для распознавания образов с помощью первичной обработки сигналов и обученной нейросетевой модели, посредством выполнения шагов (этапов), включающих:
А) первичную обработку измеренного одномерного сигнала x(t), включающую в себя:
i) удаление низкочастотного шума (так называемых, медленных дрейфовых эффектов), путем подбора коэффициентов полинома третьего порядка для точек измерений показаний сенсора xj(t) из разных термостатических областей высокой температуры. Далее из вектора сенсорного сигнала x(t) вычитается кривая γ(t), аппроксимированная на всю длину сенсорного сигнала на основе подобранных коэффициентов;
ii) корректировка локальной базовой линии внутри термостатической области низкой температуры. Такая корректировка требуется далеко не для всех векторных сигналов, а потому является опциональной.
Б) Нормировка сигнала на основе предварительно рассчитанных векторов среднего μ(t) и стандартного отклонения σ(t) выборки, на которой была обучена модель частичных наименьших квадратов (PLS), в результате получаем вектор xs(t)
В) Проекция примера на пространство «счетов» S модели частичных наименьших квадратов (PLS) через умножение на обратную матрицу «нагрузок» L-1.
Г) Оценка, является ли рассматриваемый пример выбросом через расчет расстояния в пространстве счетов относительно центра. Если это расстояние превышает выбранный порог ρ, то пример признается «выбросом» и не анализируется далее.
Д) При соответствии примера критерию в п. Г, сигнал, полученный после прохождения всех шагов пункта А подвергается процедуре так называемой «мин-макс нормировки», в ходе которой из сигнала вычитается вектор «минимального значения» xmin(t) (предварительно рассчитан на обучающей выборке), а затем результирующий вектор поэлементно делится на значения вектор «максимального значения» xmax(t) (также предварительно рассчитанного на обучающей выборке), в результате получаем вектор xm(t)
Е) Векторный сигнал подается на вход обученной регрессионной модели (нейросети (NNET)), которая определяет нормированную концентрацию водорода в газовой смеси.
Ж) Скалярное значение, полученное на шаге Е подвергается процедуре обратной нормировки, путем умножения на некоторую константу (ymax) и прибавлении значения «сдвига» (ymin), заранее рассчитанных на тренировочной выборке. В случае, если итоговое значение, полученное в ходе вышеописанных процедур выходит за рамки интервала [ymin, ymax], данное значение заменяется соответствующей (максимальной или минимальной) границей интервала.
В качестве одномерного сигнала x(t) используют значения, получаемые с измерительного оборудования в ходе циклических процедур нагрева и охлаждения сенсора по заранее заданному профилю. Образцы массива измеренного сигнала выбирают по границам предустановленного цикла, в результате чего получаются векторы данных одинаковой длины. Стоит отметить, что перечисленные модели (PLS, NNET), векторы (μ(t), σ(t), xmin(t), xmax(t)), а также критерий p были предварительно рассчитаны на основе примеров так называемой обучающей выборки - серии измерений, наблюдения которых также были подвергнуты вышеперечисленным процедурам, но и также использовались для расчета для соответствующих значений (например, среднего примеров данной выборки μ(t) и ее стандартного отклонения σ(t)) В качестве целевого параметра используют количественный параметр.
PLS модель осуществляет разложение исходного сигнала следующим образом:
Xm=SLT
Обучение моделей PLS и NNET проводят посредством минимизации внутреннего критерия - суммы квадратов регрессионных остатков на тренировочном наборе:
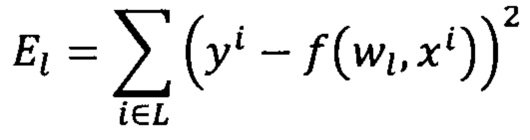
Выбор лучших моделей (при выборе гипер-парамтеров, таких как количество нейронов модели NNET и размерности вектора нагрузок PLS) осуществляют на основе внешнего критерия, рассчитанного для обученных моделей на валидационном наборе - суммы квадратов регрессионных остатков моделей, построенных на тренировочном наборе, с нормировкой на соответствующие целевые значения:
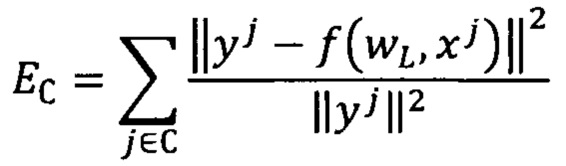
Порог ρ может быть рассчитан согласно выбранному критерию (например, ±6*σ(t)), рассчитанному в пространстве «счетов», спроецированных из примеров тренировочного набора;
Краткое описание чертежей
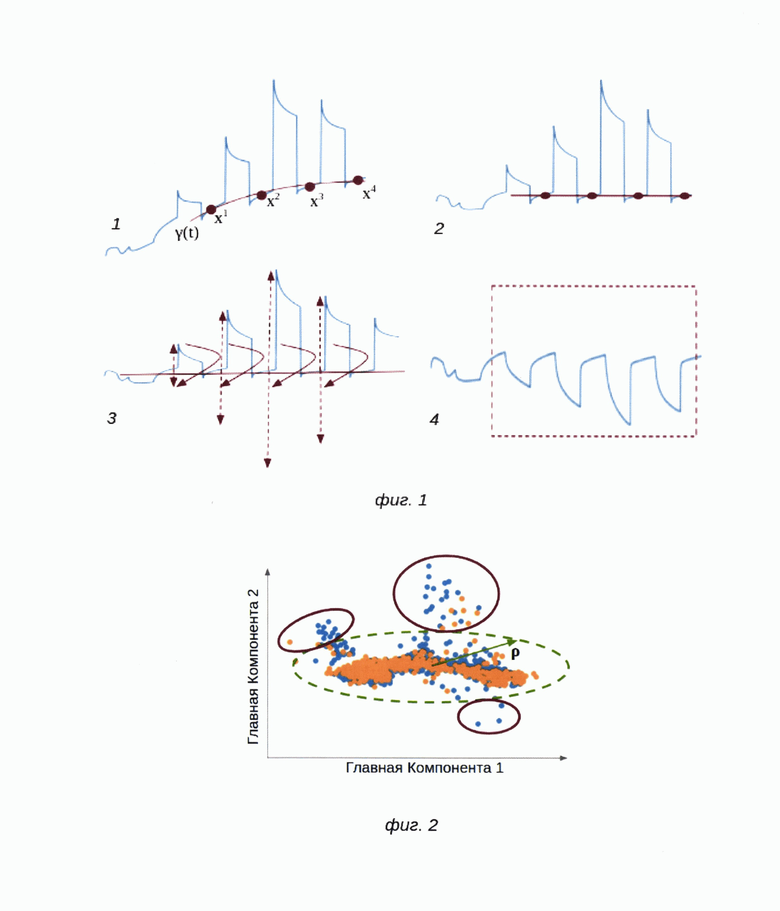
Изобретение поясняется чертежами, где на фиг. 1 представлен вид непрерывного исходного сигнала сопротивления газовых сенсоров при концентрации H2 20 ppm на протяжении 4х локальных циклов измерений (нагрев-охлаждение), полученного при реализации примера конкретного выполнения посредством заявляемого способа. Позициями на фигуре обозначены: 1 - непрерывный сигнал сопротивления (синий) и (красным схематично изображены точки (х1, х2, х3, х4) по которым будет производится подбор коэффициентов полинома и кривая γ(t), аппроксимированная вдоль всего сигнала на основе коэффициентов полинома, которая вычитается из сигнала для компенсации дрейфа); 2 - непрерывный сигнал сенсора после корректировки базовой линии (все ранее выбранные точки (выделены красным) оказались на уровне базовой линии); 3 - компенсация локального дрейфа путем вычитания из интервала низкой температуры значений, соответствующих амплитуде спайков (продемонстрирован красной стрелкой направленной вверх) при переключении термостатического режима с высокой к низкой температуре; 4 - формирование результирующего вектора измерений (вырезается вектор определенной длины для последующих процедур нормировки и обработки моделями частичных наименьших квадратов и нейросети).
На фиг. 2 представлена проекция векторов-сигналов в пространство «счетов» модели частичных наименьших квадратов, в частности представлены проекции вдоль первой и второй главных компонент. Разными цветами представлены примеры тренировочного (синий) и валидационного (оранжевый) наборов, зеленая пунктирная область выбрана на основе критерия ρ: примеры находящиеся внутри данной области -релевантные примеры, примеры, находящиеся за пределами данной области (выделены красной пунктирной линией) - «выбросы», исключаются из дальнейшего анализа.
Осуществление изобретения
Ниже представлено более детальное описание осуществления заявляемого способа, которое предназначено для пояснения сущности заявляемого изобретения. Настоящее изобретение может подвергаться различным изменениям и модификациям, понятным специалисту на основе прочтения приведенного описания. Такие изменения не ограничивают объем притязаний. Например, могут изменяться типы критериев, используемых для подстройки коэффициентов моделей, может изменяться критерий релевантности примера, объем исходных данных для подстройки параметров моделей и расчета векторов образов, используемых для процедуры нормировки (среднее, стандартное отклонение, минимальное, максимальное значения), абсолютные значения заранее заданных параметров и т.д. Способ не ограничен каким-либо типом нейронной - сети или алгоритмом обучения, а также размерностью входных данных.
Согласно способу на первом этапе (А) сигнал, соответствующий выбранному набору циклов нагрева и охлаждения сенсора, подвергают процедурам предобработки с целью удаления шума и амплитудных скачков сигнала, как показано на фиг. 1. В начале из исходного сигнала x(t) выбирается поднабор точек x=j(t) из локальных областей высоких температур, как показано на фиг. 1(1) для последующего устранения низкочастотного дрейфа вычитанием полиномов малых порядков [A. Gallant and W. Fuller. Fitting segmented polynomial regression models whose join points have to be estimated. Journal of the American Statistical Association, 68(341): 144-147, 1973]. После удаления низкочастотного дрейфа (фиг. 2(2)) наступает очередь удаления амплитудных артефактов локальных низкотемпературных областей, что продемонстрировано фиг. 1(3). Амплитудные артефакты (спайки) представляют из себя резкий подъем амплитуды сенсорного ответа при переключении режима сенсора на низкотемпературный режим. Для компенсации данного артефакта следует определить модуль амплитуды спайка и вычесть из интервала сигнала x(t), соответствующего данной локальной области низких температур. Поскольку спайковый артефакт может наблюдаться на протяжении нескольких точек измерения, для его точной локализации можно использовать подход определения границ на основе фильтров, известных из уровня техники (например, одномерный Собел-фильтр [В. Jähne, Н. Scharr, and S. Korkel. Principles of filter design. In Handbook of Computer Vision and Applications. Academic Press, 1999]). Внутри границ области резкого возрастания сенсорного ответа рассчитывается кумулятивная сумма и затем это значение вычитается из соответсвующей локальной области низкой температуры. Описанная выше процедура компенсации амплитудных артефактов проводится независимо для каждой локальной области низких температур; в заключение края векторного сигнала могут быть удалены согласно заранее определенным координатам, для получения итогового вектора определенной размерности, необходимой для корректной работы моделей частичных наименьших квадратов и нейронной сети, как показано на примере фиг. 1(4).
На этапах Б-Г с векторным сигналом производятся манипуляции, необходимые для оценки его релевантности решаемой задаче, да бы быть уверенными в корректности итогового ответа системы. Для этого на этапе Б сигнал подвергают стандартной процедуре автошкалирования [R. Wehners. Chemometrics with R: Multivariate Data Analysis in the Natural Sciences and Life Sciences (Use R!). Springer, p. 300, 2011] и преобразования в пространство счетов модели (этап В) частичных наименьших квадратов [Haenlein, Michael; Kaplan, Andreas, M. (2004). "A Beginner's Guide to Partial Least Squares Analysis". Understanding Statistics. 3(4): 283-297], которая в данном случае используется для детектирования так называемых «выбросов», что также является известным из уровня техники подходом [Rousseeuw, P. J., Debruyne, М., Engelen, S., & Hubert, М. (2006). Robustness and outlier detection in chemometrics. Critical reviews in analytical chemistry. 36(3-4), 221-242]. Процедура детектирования выбросов (этап Г) заключается в оценке координаты рассматриваемого образца в низкоразмерном пространстве «счетов» модели частичных наименьших квадратов, относительно допустимой области, определенной критерием р, как проиллюстрировано на фиг. 2. Отметим, что хотя пространство главных компонент является ортогональным, однако значимость координат пространства убывает с увеличением их порядкового номера, что может приводить к значительным различиям в амплитудном размахе значений вдоль главных компонент, в связи с чем критерий может вычисляться на основании расстояния Махаланобиса [De Maesschalck, R.; D. Jouan-Rimbaud, D.L. Massart (2000) The Mahalanobis distance. Chemometrics and Intelligent Laboratory Systems 50: 1-18] или более консервативного критерия, например выход за пределы интервала ±3σ относительно любой из старших главных компонент
На этапах Д-Ж производится нормировка векторного сигнала, полученного в результате осуществления этапа А (этап Д) и последующее применение искусственной нейронной сети (этап Е) и конвертацией ее ответа в согласованные физические единицы (этап Ж). Применение искусственных нейронных сетей соответствует мировому уровню техники [Leijnen, S., & Veen, F.V. (2020). The neural network zoo. Multidisciplinary Digital Publishing Institute Proceedings, 47(1), 9.], однако выбор конкретной архитектуры (или ансамбля моделей с различными архитектурами) и параметров нейронной сети представляется отдельной исследовательской задачей, решаемой на подготовительном этапе, представленном ниже. Хорошо известно, что выбор той или иной архитектуры нейроннойсети и ее передаточных функций напрямую влияет на процедуры нормировки [Adeyemo, A., Wimmer, Н., & Powell, L.М. (2019). Effects of normalization techniques on logistic regression in data science. Journal of Information Systems Applied Research, 12(2), 37.], однако в связи с тем, что представленное изобретение используется для обработки сигналов выравненных по базовой линии (на этапе А), а целевым параметром является концентрация водорода, которая имеет вполне определенное нулевое значение, то для этапов Д-Ж предлагается использовать «мин-макс» нормировку и передаточные функции нейронной сети, нижней границей значений которых является 0.
Целью вышеуказанного подготовительного этапа является обучение моделей частичных наименьших квадратов (используемой на этапе В) и нейронной сети (используемой на этапе Е), а также расчета нормировочных коэффициентов для этапов Б, Д, Ж и критерия оценки релевантности примера этапа Г. Для реализации данного этапа на протяжении длительного времени производятся измерения сенсорных показаний для разных концентраций водорода, задаваемых на экспериментальной установке; каждое измерение состоит из набора температурных циклов охлаждение-нагрев, общие температурные профили температурных циклов идентичны относительно разных измерений. Все примеры измерений разделяются на тренировочный (первые 90% всех измерений, расположенных хронологически) и валидационный наборы (последние 10% всех измерений, расположенных хронологически) Т. Hastie, R. Tibshirani, J. Friedman, The Elements of Statistical Learning, Springer-Verlag New York, 745 p. 2009], затем подвергаются процедурам описанным для этапа А, в результате чего получаются наборы Xtrain и Xval и соответствующие им наборы концентраций Ytrain и Yval. Для массива тренировочных образцов рассчитываются нормировочные константные векторы (минимальный (xmin(t)), максимальный (xmax(t)), средний μ(t), стандартное отклонение σ(t)) и граничные значения минимальной и максимальной концентраций (ymin и ymax, соответственно). Затем измерения из наборов измерений и концентраций подвергаются процедурам нормировки, описанным на этапах Б и Д, для подбора параметров моделей частичных наименьших квадратов и нейронной сети, соответственно. Процедура непосредственного подбора коэффициентов модели производится с помощью метода наименьших квадратов Т. Hastie, R. Tibshirani, J. Friedman, The Elements of Statistical Learning, Springer-Verlag New York, 745 p. 2009] или градиентного спуска [Bishop, C.M. Pattern Recognition and Machine Learning. - Springer, 2006. - 738 p,], целевой функцией которого является минимизация на каждой итерации обучения внутреннего критерия среднеквадратичного отклонения значений, предсказанных моделью на основе поданных измерений, относительно соответствующих реальных значений целевого параметра. Выбор же оптимальных параметров модели (таких как количество главных компонент модели частичных наименьших квадратов или тип архитектуры и количество скрытых слоев нейронной сети) осуществляется на основе внешнего критерия (суммы квадратов регрессионных остатков моделей, построенных на тренировочном наборе, с нормировкой на соответствующие целевые значения), рассчитываемого однократно для обученной модели на валидационной выборке примеров.
Для демонстрации эффективности разработанного подхода был проведен цикл измерений состава воздуха с помощью прототипа полупроводникового газового сенсора производства ООО «Олфактум» (Россия). Сенсоры работали в непрерывном режиме, частота дискретизации сигнала составляла 0.1 сек, при этом было реализовано циклическое изменение их температуры, как показано на фиг. 1. Продолжительность цикла измерения составляет 60 секунд, в течение которых температура сенсора ступенчато варьируется от 300 до 450°С, что позволяет обеспечить протекание реакции с водородом, а также восстановить поверхность чувствительного элемента до исходного состояния. Перед началом каждого эксперимента проводили продувку камеры с сенсором синтетическим имитатором альвеолярного воздуха (кислород 14% об, углекислый газ 6% об, азот - остальное, отн. влажность не менее 80%) без примеси водорода в течение 10 минут. Измерения для заданного типа газа осуществляли по 40 минут, прерывая их 20-минутными продувками установки синтетическим имитатором альвеолярного воздуха. В ходе каждого такого временного отрезка ток воздуха через сенсорную камеру чередовался с формированием неподвижной атмосферы с помощью переключения клапанов газового стенда для имитации применения анализатора человеком. Чередование тока воздуха и неподвижной атмосферы осуществлялось каждые 2 минуты. Таким образом проводилась регистрация двух последовательных циклов работы в режиме тока и неподвижного воздуха и для каждой концентрации водорода в ходе одного эксперимента накапливалось по 20 откликов. Основная масса экспериментов проводилась по следующим двум чередующимся схемам: 1) Концентрации H2 последовательно уменьшаются в ряду 200-190-180-170-160-150-140-130-120-110-100-90-70-60-50-40-30-20-10-5-3-1 млн-1.
2) Концентрации H2 последовательно уменьшаются в ряду 195-185-175-165-155-145-135-125-115-105-95-85-75-65-55-45-35-25-15-7-4-2 млн-1.
Таким образом, один эксперимент по накоплению данных имел продолжительность порядка 25 часов. Величина потока через сенсорную камеру поддерживалась постоянной в течение всего эксперимента во всех экспериментах на уровне 50 мл/мин. Эти две схемы проведения экспериментов по формированию базы данных откликов были расширены за счет добавления в ток альвеолярного воздуха сероводорода в концентрации 0,25, 0,5 и 1 млн-1. Таким образом общий перечень различных типов экспериментов, проводившихся при составлении базы данных откликов сенсора, составил 8 штук. Всего было проведено 14 экспериментов.
В ходе реализации вычислительной части на тренировочном наборе данных была реализована модель на основе нейросети с 128 нейронами, а также на основе метода наименьших квадратов с оптимальными параметрами, рассчитанными на основе валидационного набора с использованием внешнего критерия. Каждый из образцов данных подвергался предварительной обработке согласно пп. А, В, Г, Д, Е, Ж раскрытия изобретения, в результате чего была получена количественная оценка искомого параметра - концентрация водорода.
Для технической реализации вычислительного алгоритма использовали компьютер на базе процессора intel 8250U, видеокарта nvidia gtx 1050ti, 16gb ram на базе операционной системы linux. Использование графического ускорителя, библиотек numpy, sklearn, pytorch языка python позволили ускорить вычисления и организовать многопоточные вычисления.
Таким образом, преимущество разработанного подхода было продемонстрировано в возможности решения как задачи определения типа газа, так и определения концентраций отдельных газов и их смеси. По сравнению с известным способом по патенту US 8064722 B1, заявляемый способ, помимо возможности определения типа газа (качественного целевого параметра), позволяет определять концентрацию исследуемых газов (количественного целевого параметра), а также обеспечивает высокую точность определения целевого параметра (качественного или количественного) с возможностью отказа детектирования выбросов и отказа от распознавания.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОБРАБОТКИ ВЕКТОРНЫХ СИГНАЛОВ ДЛЯ РАСПОЗНАВАНИЯ ОБРАЗОВ НА ОСНОВЕ ВЕЙВЛЕТ-АНАЛИЗА | 2017 |
|
RU2690001C1 |
| СПОСОБ И СИСТЕМА КОНЕЧНОГО АВТОМАТА ДЛЯ РАСПОЗНАВАНИЯ РАБОЧЕГО СОСТОЯНИЯ СЕНСОРА | 2018 |
|
RU2744908C1 |
| Способ анализа медицинских данных с помощью нейронной сети LogNNet | 2021 |
|
RU2754723C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ МОШЕННИЧЕСКИХ ТРАНЗАКЦИЙ ПОЛЬЗОВАТЕЛЯ | 2024 |
|
RU2839053C1 |
| СПОСОБ ТЕСТ-ИДЕНТИФИКАЦИИ МНОГОКОМПОНЕНТНЫХ ГАЗОВЫХ СМЕСЕЙ БЕНЗОЛА, ТОЛУОЛА, ФЕНОЛА, ФОРМАЛЬДЕГИДА, АЦЕТОНА И АММИАКА | 2011 |
|
RU2456590C1 |
| СПОСОБ И СИСТЕМА КЛАССИФИКАЦИИ ДАННЫХ ДЛЯ ВЫЯВЛЕНИЯ КОНФИДЕНЦИАЛЬНОЙ ИНФОРМАЦИИ В ТЕКСТЕ | 2019 |
|
RU2755606C2 |
| СПОСОБ СОЗДАНИЯ МОДЕЛИ АНАЛИЗА ДИАЛОГОВ НА БАЗЕ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА ДЛЯ ОБРАБОТКИ ЗАПРОСОВ ПОЛЬЗОВАТЕЛЕЙ И СИСТЕМА, ИСПОЛЬЗУЮЩАЯ ТАКУЮ МОДЕЛЬ | 2019 |
|
RU2730449C2 |
| НЕЙРОННАЯ ТОЧЕЧНАЯ ГРАФИКА | 2019 |
|
RU2729166C1 |
| Способ определения направления на цель цифровой антенной решеткой моноимпульсной радиолокационной станции | 2021 |
|
RU2761106C1 |
| СПОСОБ ФОРМИРОВАНИЯ СИСТЕМЫ УПРАВЛЕНИЯ МОЗГ-КОМПЬЮТЕР | 2019 |
|
RU2704497C1 |
Изобретение относится к способу обработки данных. Технический результат направлен на повышение точности обработки сигналов. Способ обработки векторных сигналов для распознавания образов на основе нейронных сетей с детектирование выбросов, включает A) получение массива образцов измеренного сигнала для формирования обучающей выборки, Б) первичную обработку измеренного одномерного сигнала x(t) посредством: i) удаления низкочастотного шума; ii) локальной корректировки базовой линии внутри областей стационарных областей низкой температуры. На этапе B) производят последующую нормировку предобработанного сигнала; Г) нормированный согласно п. В) образец затем проецируется на пространство счетов S модели PLS путем; Д) для каждого образца оценивается его релевантность решаемой задачи, Е) частое наблюдение «выбросов» по п. Д) говорит о систематических проблемах измерительной установки или математической модели; Ж) в случае если образец удовлетворяет критерию п. Д), далее он подвергается так называемой «мин-макс» нормировке, З) образец, подвергнутый обработке по п. Ж), подается на вход нейронной сети; И) значение, полученное в результате применения нейронной сети по п. З), подвергается обратной «мин-макс» нормировке, путем умножения на максимальное значение концентрации ymax(t) и прибавления минимального значения ymin(t) концентраций водорода (скалярные значения ymin(t) и ymax(t) концентраций водорода заранее рассчитаны на основе тренировочной выборки примеров по п. А), которое представляет собой искомое целевое значение концентрации водорода. 14 з.п. ф-лы, 2 ил.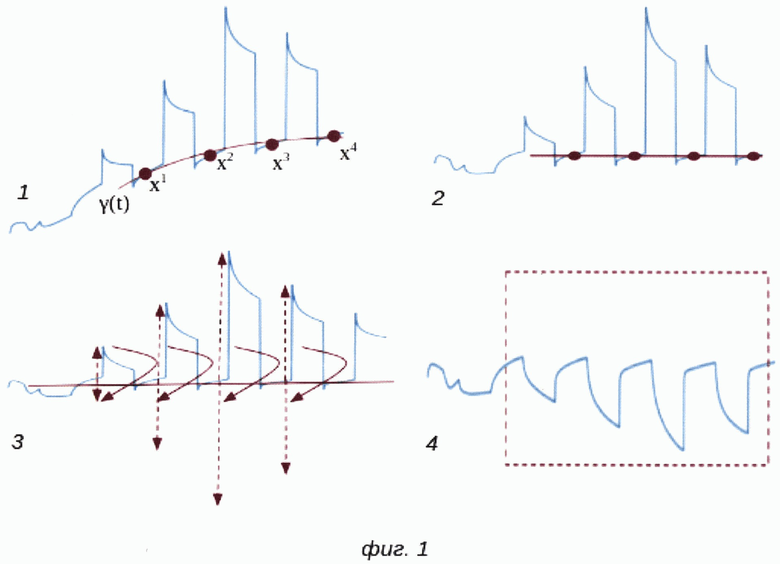
1. Способ обработки векторных сигналов для распознавания образов на основе нейронных сетей с детектированием выбросов, включающий
A) получение массива образцов измеренного сигнала для формирования обучающей выборки, разделенной на тренировочный, валидационный и тестовый набор, где каждому образцу измеренного сигнала сопоставляют известное значение по меньшей мере одного целевого параметра;
Б) первичную обработку измеренного одномерного сигнала x(t) посредством:
i) удаления низкочастотного шума (медленного дрейфа);
ii) локальной корректировки базовой линии внутри областей стационарных областей низкой температуры;
B) последующую нормировку предобработанного сигнала путем вычитания среднего μ(t) и поэлементного деления на стандартное отклонение σ(t) (заранее рассчитанных на основе тренировочной выборки примеров по п. А);
Г) нормированный согласно п. В) образец затем проецируется на пространство счетов S модели PLS путем матричного умножения на обратную матрицы нагрузок LT (коэффициенты которой заранее рассчитаны на тренировочном наборе по п. А в рамках формирования PLS-модели);
Д) для каждого образца оценивается его релевантность решаемой задачи, согласно критерию ρ в пространстве счетов по п. Г); в случае несоответствия критерию образец признается «выбросом» и не подвергается дальнейшему анализу;
Е) частое наблюдение «выбросов» по п. Д) говорит о систематических проблемах измерительной установки или математической модели, в связи с чем рекомендуется остановить наблюдения, выявить и устранить неисправность;
Ж) в случае если образец удовлетворяет критерию п. Д), далее он подвергается так называемой «мин-макс» нормировке, путем поэлементного вычитания минимального xmin(t) и деления на максимальное xmax(t) значения образов (векторы xmin(t) и xmax(t) заранее рассчитаны на основе тренировочной выборки примеров по п. А);
З) образец, подвергнутый обработке по п. Ж), подается на вход нейронной сети (значения обучаемых параметров и архитектура предварительно рассчитаны на тренировочной выборке по п. А, лучший набор параметров выбран на основе внешнего критерия, рассчитанного на валидационном наборе);
И) значение, полученное в результате применения нейронной сети по п. З), подвергается обратной «мин-макс» нормировке, путем умножения на максимальное значение концентрации ymax(t) и прибавления минимального значения ymin(t) концентраций водорода (скалярные значения ymin(t) и ymax(t) концентраций водорода заранее рассчитаны на основе тренировочной выборки примеров по п. А), которое представляет собой искомое целевое значение концентрации водорода.
2. Способ по п. 1, характеризующийся тем, что в качестве одномерного сигнала x(t) используют значения, получаемые с измерительного оборудования.
3. Способ по п. 1, характеризующийся тем, что низкочастотный шум (медленный дрейф базовой линии) удаляют с использованием полиномиальной модели.
4. Способ по п. 1, характеризующийся тем, что производится локальная корректировка базовой линий для стационарных областей низкой температуры путем вычитания из диапазона амплитуды спайков, наблюдаемых в момент охлаждения сенсора.
5. Способ по п. 1, характеризующийся тем, что нормирование предобработанного сигнала осуществляют посредством вычитания вектора «минимального сигнала» и деления значений сигнала в каждой точке на вектор «максимального сигнала» рассчитанных на «обучающей выборке» ранее измеренных сигналов.
6. Способ по п. 1, характеризующийся тем, что образцы массива измеренного сигнала выбирают одинаковой длины.
7. Способ по п. 1, характеризующийся тем, что образцы измеренного сигнала проецируются в пространство счетов модели PLS.
8. Способ по п. 1, характеризующийся тем, что образцы массива измеренного сигнала могут быть отклонены как не релевантные, на основе критерия, рассчитанного в пространстве векторов «счетов» модели PLS.
9. Способ по п. 1, характеризующийся тем, каждый из наборов массива образцов измеренного сигнала - тренировочного и валидационного, формируют из подмножества образцов измерений, полученных в ходе экспериментов, проведенных в разное время.
10. Способ по п. 1, характеризующийся тем, что в качестве целевого параметра используют количественный параметр.
11. Способ по п. 1, характеризующийся тем, что модель PLS представляет массив сигналов:
Xm=SLT,
где Xm - матрица исходных сигналов, S - матрица счетов (проекций образцов сигнала в пространство меньшей размерности), LT - матрица нагрузок (проекций координат многомерного сигнала в пространство меньшей размерности).
12. Способ по п. 1, характеризующийся тем, что в качестве модели для определения количественного параметра используется нейронная сеть.
13. Способ по п. 1, характеризующийся тем, что предварительное обучение моделей проводят посредством минимизации внутреннего критерия - суммы квадратов регрессионных остатков на тренировочном наборе:
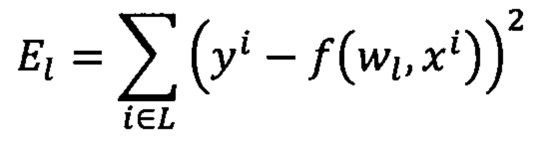
14. Способ по п. 1, характеризующийся тем, что минимизацию внутреннего критерия для модели PLS осуществляют с помощью алгоритма наименьших квадратов:
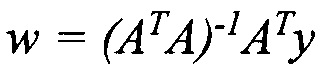
15. Способ по п. 1, характеризующийся тем, что подбор гиперпараметров для обучаемых моделей проводится на основе отбора лучших моделей, выбор которых осуществляют на основе внешнего критерия, рассчитанного на валидационном наборе - суммы квадратов регрессионных остатков моделей, построенных на тренировочном наборе, с нормировкой на соответствующие целевые значения:
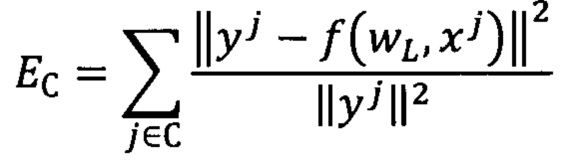
| US 11593650 B2, 28.02.2023 | |||
| Способ получения продуктов конденсации фенолов с формальдегидом | 1924 |
|
SU2022A1 |
| Способ регенерирования сульфо-кислот, употребленных при гидролизе жиров | 1924 |
|
SU2021A1 |
| СПОСОБ ОБРАБОТКИ ВЕКТОРНЫХ СИГНАЛОВ ДЛЯ РАСПОЗНАВАНИЯ ОБРАЗОВ НА ОСНОВЕ ВЕЙВЛЕТ-АНАЛИЗА | 2017 |
|
RU2690001C1 |
| Способ и система для прогнозирования значений временного ряда с использованием искусственной нейронной сети | 2019 |
|
RU2744041C1 |
Авторы
Даты
2024-11-14—Публикация
2024-01-25—Подача