Область техники
Настоящее изобретение относится к методам обработки данных, используемых для построения систем, позволяющих решать задачи распознавание образов, классификации и количественного содержания целевого параметра (регрессии), на основе измерений, представляющих из себя непрерывные одномерные сигналы, с использованием вейвлетного анализа для обучения адаптивной модели.
В частности, изобретение может быть использовано для определения газов и их концентрации на основе сигналов, например, с полупроводниковых сенсоров; определения типов неорганических соединений и их концентраций в растворах на основе методов спектроскопии; и др.
Уровень техники
Из уровня техники известны способы, обеспечивающие решение задач распознавания образов, классификации и определения количественного содержания целевого параметра, после проведения, так называемой, процедуры обучения с учителем на массиве соответствующих решаемой задаче входных и выходных данных, итеративно подаваемых в систему.
В частности, известен способ определения типов газов, измеренных на массиве сенсоров с адаптивными регрессионными алгоритмами и компьютерно-реализуемая система (US 2006/0155486 А1). Согласно способу измеряют сопротивление металл-оксидных сенсоров, определяют интервалы показаний на протяжении отдельных циклов работы сенсоров в процессе их нагрева от температуры окружающей среды до температуры 1000°C, в качестве регрессоров используют алгоритмы многомерной линейной регрессии и ПЛС (проекций на латентные структуры или частичных наименьших квадратов), проводят процедуру предобработки исходных данных на основе простых математических операций логарифмирования, потенцирования, а также ограничивают масштаб изменений последовательно измеряемых значений. Также, проблему нестационарных дрейфовых эффектов, проявляющихся в измеренном сигнале, решают посредством локальных линейных регрессоров, задачей которых является корректировка локально возникающих трендов. Многомерные регрессионные модели использовались в сходных задачах, описанных в патентах US 007142105 B2, US 2016/0132617 A1, US 2016/0231229 А1, определения концентраций и типов газов на основе спектроскопических измерений. Помимо линейных моделей для определения типов и концентраций газовых смесей известно использование нелинейного метода К-ближайших соседей (US 2013/0197384 A1), с помощью которого была продемонстрирована возможность диагностики респираторных заболеваний путем определения компонент газовой смеси по показаниям surface acoustic wave sensors. Решение на основе выбранного алгоритма (способа) сравнивалось с результатом модели обученной искусственной нейронной сети - еще одного популярного метода, обладающего свойствами универсальной аппроксимации функций и имеющего широкое применение: например в задаче определения загрязнений воздуха (US 2016/0125307 A1) и поиска областей утечки газов из баллонов (US 2014/0165729 A1). Недостатком известных технических решений является избыточность числа параметров модели, что затрудняет процесс их подбора и снижает обобщающие способности моделей. Данная проблема возникает в связи с зависимостью числа параметров нейронной сети от числа входных переменных, поскольку в отличие от простых линейных моделей в нейронной сети связь между входными и выходными переменными осуществляется через, так называемые, скрытые слои нейронов, в которых осуществляется применение некоторой заданной передаточной функции к взвешенной сумме значений предыдущего слоя, в данном случае - входных признаков. Таким образом, количество параметров нейронной сети равно сумме произведений числа нейронов каждого слоя с ближайшим предыдущим, т.е., если на вход нейронной сети подаются примеры сигналов, состоящих из 100 точек и при этом нейронная сеть содержит 10 нейронов в единственном скрытом слое и предсказывает 2 выходных значения, решая тем самым задачу бинарной классификации, то количество параметров модели увеличивается до значения 100*10+10*2=1020.
Кроме того, существенным недостатком сложных нелинейных методов, к которым относятся и нейронные сети, является их плохая устойчивость к наличию шумов в сигнале, подаваемом на входной слой нейронной сети. Присутствие шумов характерно для сигналов реальных измерений. Для борьбы с шумами и дрейфовыми эффектами применяют большое количество различных методик: разреженное представление исходных сигналов с помощью случайного гауссова распределения (US 2016/0123943 A1) для последующей фильтрации значений обучении нейронной сети на выбранных признаках; аппроксимацию полиномами Лагранжа исходного сигнала массива сенсоров и анализ параметров аппроксимирующей модели (US 2013/0064423 А1); нейронные сети автоассоциативной памяти для устранения шумов и эффективного сжатия подаваемых примеров сигналов биоэлектрической активности, записанной с помощью ЭЭГ (электроэнцефалограмма) и МЭГ (магнитоэнцефалограмма) (US 8725669 B1); добавление шума в обучающую выборку, параметры распределения которого подбирают с генетическим алгоритмом (US 20030191728 A1). Указанные подходы также имеют ряд существенных недостатков, затрудняющих их использование: полиномы Лагранжа хорошо описывают гладкие функции, однако будут испытывать серьезные трудности в случае наличия резких локальных изменений уровня сигнала, что является довольно характерным явлением для тех же газовых сенсоров при переключении нагревательного элемента сенсора на охлаждение. Нейронная сеть автоассоциативной памяти требует огромной обучающей выборки ввиду большого количества параметров, при этом в любом случае может проявляться отсутствие формальных ограничений на ее ответы и потенциальная опасность переучивания системы на одном типе дисторсии сигнала, после чего система будет пытаться устранить именно ее независимо от ее наличия или присутствия других типов шумов и смещений базовой линии. Реализация с генетическим алгоритмом предполагает обучение нейронных сетей после каждой итерации добавления шума, говоря терминами генетических алгоритмов: после генерации поколения индивидуумов, т.е. набора выборок с несколько отличающимися параметрами распределения, на каждой из которых потребуется обучения нейронной сети. Основным недостатком данного подхода является необходимость обучения огромного числа нейросетевых моделей, что требует наличия значительных вычислительных ресурсов и времени вычислений.
Более классическими методами устранения шумов в измеряемом сигнале являются спектральные методы, базирующиеся на фурье-преобразовании. Существенным недостатком такого представления сигнала является утеря его локальной структуры. Данный недостаток был устранен в рамках развивающейся с конца 80х годов теории вейвлетов, а именно введением требований ограниченности, локализованности и ортогональности на функции-вейвлеты, с которыми осуществляется свертка. Последнее позволяет реконструировать сигнал после удаления некоторых компонент в вейвлет-пространстве, что является классической техникой для устранения шумов в сигнале. Подобный механизм был применен в патентах US 2015/0149119 А1, US 6211515 B1, US 6647252, где осуществляется отсечка коэффициентов жестким порогом на определенных уровнях детализации. Однако такой подход может оказаться неэффективным, поскольку подобная процедура отсекает лишь заданный набор частот и амплитуд, тогда как дисторсия может иметь более сложный характер, для чего следует применять более сложные механизмы по отбору вейвлет-коэффициентов. Таким образом, после отсечения шумовых компонент сигнала в пространстве вейвлет коэффициентов можно не реконструировать сигнал, а использовать отобранные вейвлет-коэффициенты для решения конечной задачи. В качестве методов отбора в патентах US 2016/0305865 и US 8064722 использовался метод главных компонент, переводящий данные в новые координаты, соответствующие направлениям максимальной дисперсии. В патенте US 8064722 в качестве альтернативы был использован дисперсионный анализ (ANOVA) для выбора тех вейвлет-коэффициентов, которые изменяются в зависимости от состава газовой смеси (целевого параметра). Полученные таким образом переменные использовались в качестве входных признаков для решения конечной задачи определения типа газов алгоритмами классификации: K-ближайших соседей (US 2016/0305865); нейронные сети и метод линейного дискриминантного анализа (US 8064722). Следует отметить, что вейвлет-преобразование на каждом уровне детализации фактически производит понижение размерности данных (например, результатом классического алгоритма дискретного вейвлет-преобразования сигнала N переменных являются N/2j вейвлет-коэффициентов на каждом уровне детализации j) и эффективное решение конечной задачи может быть получено путем прямого использования вейвлет-коэффициентов в качестве входных признаков классификатора (нейронной сети), минуя дополнительные процедуры отбора признаков (US 2011/0071376 A1 и US 8595164). Предполагается, что существенные признаки будут выбраны самой нейронной сетью на этапе обучения, тогда как малозначительным переменным будут присвоены минимальные весовые коэффициенты и их присутствие не будет сказываться работе системы.
Альтернативным подходом к выбору существенных признаков является подход алгоритма метода группового учета аргумента (МГУА), использующий стратегию итеративного усложнения математической модели полиномиальной регрессии, реализуемой в рамках так называемого многорядного алгоритма. Данный алгоритм был применен для выбора существенных локальных областей из изображений в патенте US 7076098 B2.
Свойства вейвлет-функций позволяют использовать их не только для моделирования сигналов, но и поверхности функции отображения входных переменных на выходные, формируя так называемые вейвлоны - узлы сети обратного распространения, в отличие от классической нейронной сети представляющие из себя не преобразование взвешенной суммы входных признаков, а их множественное произведение, члены которого есть вейвлет-преобразование данных признаков. Параметры масштаба и положения подстраиваются на основе алгоритма градиентного спуска, поэтому на вейвлет-функции накладывается ограничение дифференцируемости. К недостаткам вейвлет нейронных сетей можно отнести невозможность работы с входными данными большой размерности, поскольку эта же размерность будет соответствовать количеству слагаемых в вейвлоне, в связи с чем, будет затруднен процесс корректировки параметров вейвлонов в процесс обучения. В связи с указанной проблемой данный алгоритм применяется в задачах, оперирующих лишь несколькими переменными, как например, в патенте US 2016/0161448 A1, оперирующий с датчиками потока магнитного поля по трем пространственным координатам.
Наиболее близким к заявляемому решению является способ и система для анализа сигнала сенсоров, представленного в векторной форме, для распознавания образов (US 8064722 B1). Способ включает создание тренировочного массива данных, нормализацию и трансформацию этого массива в вейвлет-коэффициенты; отбор существенных признаков с помощью анализа вариации, распознавание образов в рамках решения задачи классификации - определения газового состава осуществляют по отобранным вейвлет-коэффициентам.
Однако отбор существенных вейвлет-коэффициентов в известном способе проводится с помощью метода дисперсионного анализа, что предполагает простые линейные связи между входными и выходными значениями; однако их связь может иметь более сложный характер, из-за чего в линейном приближении некоторые существенные признаки могут быть отброшены, что негативно сказывается на точности получаемого результата.
Раскрытие изобретения
Задачей настоящего изобретения является создание способа обработки данных векторных сигналов для распознавания образов на основе вейвлет-анализа, обеспечивающего выделение наиболее важных участков исходного сигнала для решения задачи определения целевого параметра.
Техническим результатом изобретения является возможность определения целевого параметра (качественного или количественного), устойчивого к присутствию шумовой составляющей, за счет выделения из измеряемых сигналов разномасштабных участков, наиболее релевантных решаемой задаче с высокой устойчивостью к искажению сигнала.
Поставленная задача решается обработкой векторных сигналов для распознавания образов на основе вейвлет-анализа, посредством выполнения шагов (этапов), включающих:
A) первичную обработку измеренного одномерного сигнала x(t) посредством удаления высокочастотного шума, с последующим нормированием предобработанного сигнала с получением массива образцов измеренного сигнала для формирования обучающей выборки, разделенной на тренировочный, валидационный и тестовый набор, где каждому образцу измеренного сигнала сопоставляют известное значение, по меньшей мере, одного целевого параметра;
Б) для каждого образца из полученного массива обучающей выборки определяют окна текущего уровня детализации, соответствующих заданным значением параметров ширины s и положения их центров - t, с обеспечением перекрытия соседних окон;
B) каждый образец из полученного массива обучающей выборки обрабатывают с помощью вейвлет-преобразования, с осуществлением свертки вейвлет-функций по перекрывающимся окнам данного уровня детализации с получением вейвлет-коэффициентов (a1…an);
Г) выбирают опорную функцию, максимальное количество ее переменных, с последующим построением семейства моделей для отображения с помощью выбранной функции вейвлет-коэффициентов (a1…an) на, по меньшей мере, одно целевое значение;
Д) после чего каждую модель из семейства по п. Г) обучают на тренировочном наборе с подбором весовых параметров моделей w1…wn и последующим выбором лучших моделей по критерию, рассчитанному на валидационном наборе;
Е) проверку выбранных моделей на шаге Г) на тестовой выборке путем расчета критерия оценки сходимости алгоритма;
Ж) выбор значимых участков, соответствующих окнам данного уровня детализации,
З) переход к следующему уровню детализации внутри выбранных по п. Ж) значимых участков - окон текущего уровня детализации, соответствующих лучшим моделям, содержащим вейвлет-коэффициенты аi, ранее рассчитанным внутри этих окон;
И) для каждого окна из значимых участков, определенных на первом уровне детализации, применяют соответствующее вейвлет-преобразование с меньшим параметром масштаба с получением детализированного представления набора значимых участков,
после чего этапы В)-И) повторяют до достижения критерия сходимости, определяемого по значению целевой функции на тестовом наборе, в результате чего получают набор парных комбинаций s и t, соответствующих значимым участкам измеренного сигнала, по которым определяют искомый целевой параметр.
В качестве одномерного сигнала x(t) используют значения, непрерывно получаемые с измерительного оборудования. Высокочастотный шум удаляют с использованием медианного фильтра. Нормирование предобработанного сигнала осуществляют посредством деления значений сигнала в каждой точке на интегральное значение измеренного сигнала. Образцы массива измеренного сигнала выбирают одинаковой длины. Каждый из наборов массива образцов измеренного сигнала - тренировочного, тестового и валидационного, формируют из подмножества образцов измерений, полученных в ходе экспериментов, проведенных в разное время. В качестве целевого параметра используют количественный или качественный параметр.
Вейвлет-преобразовние представляет собой
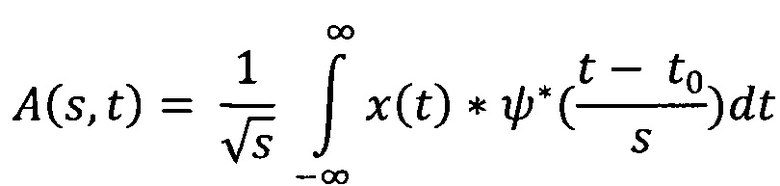
где x(t) - исходный сигнал, ψ* - комплексно-сопряженная материнская вейвлет-функция.
В качестве вейвлет-функции используют функции, удовлетворяющими следующим свойствам: локализации; нулевого среднего; ограниченности; дифференцируемости; самоподобия.
Перекрытие соседних окон составляет не менее 30% от ширины окна.
Свертку сигнала с вейвлет-функцией осуществляют в фурье-пространстве, для чего: вычисляют Фурье-образ дискретных сигналов, представляющих из себя последовательности значений {xn}:
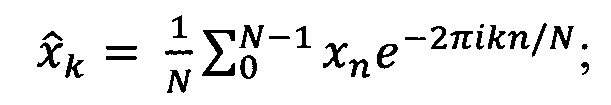
вычисляют Фурье-образ вейвлет-функции:
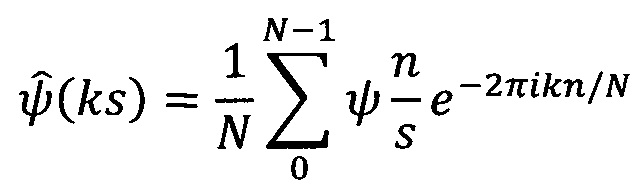
умножают Фурье-образ дискретных сигналов на комплексно-сопряженный Фурье-образ вейвлет-функции и производят обратное Фурье-преобразование:
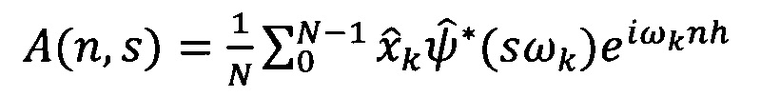
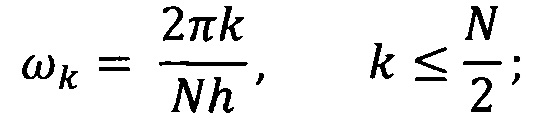
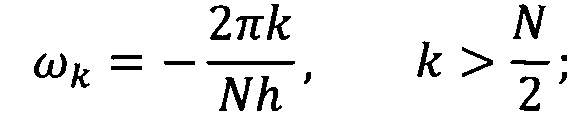
где n - 0, 1, …, N-1, N - число отсчетов в исследуемом ряду данных; h - интервал между последовательными отсчетами временного домена, k/h ⊂ (0, …, (N-1)/h) образует множество частот исходного сигнала xn.
В качестве опорной функции выбирают линейную функцию, состоящую из членов нулевого и первого порядка:
y0=w00
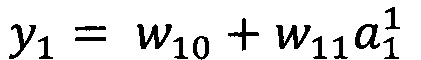
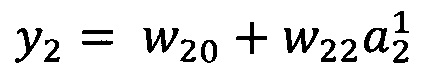
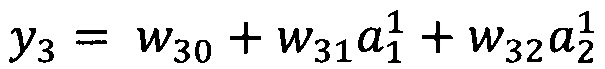
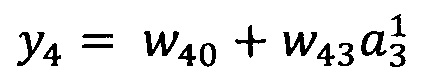
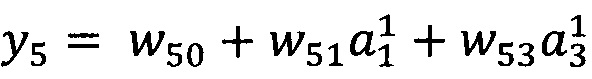
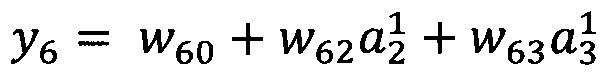
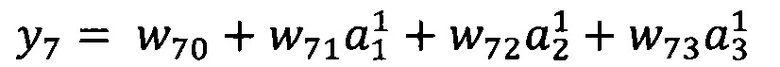
Обучение проводят посредством минимизации внутреннего критерия - суммы квадратов регрессионных остатков на тренировочном наборе:
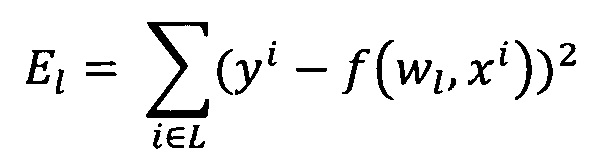
Минимизацию внутреннего критерия осуществляют с помощью алгоритма наименьших квадратов:
w=(ATA)-1ATy
Выбор лучших моделей осуществляют на основе внешнего критерия, рассчитанного на валидационном наборе - суммы квадратов регрессионных остатков моделей, построенных на тренировочном наборе, с нормировкой на соответствующие целевые значения:
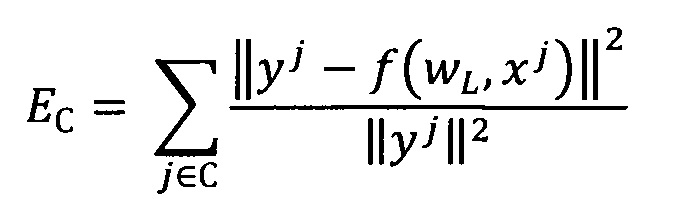
Из построенного семейства моделей выбирают четвертую часть моделей, являющихся лучшими по оценке внешнего критерия на валидационном наборе.
Переход к следующему уровню детализации осуществляют лишь в том случае, если точность определения целевого параметра на тестовом наборе для хотя бы одной из отобранных моделей превзошла результаты, полученные на предыдущем уровне детализации;
Краткое описание чертежей
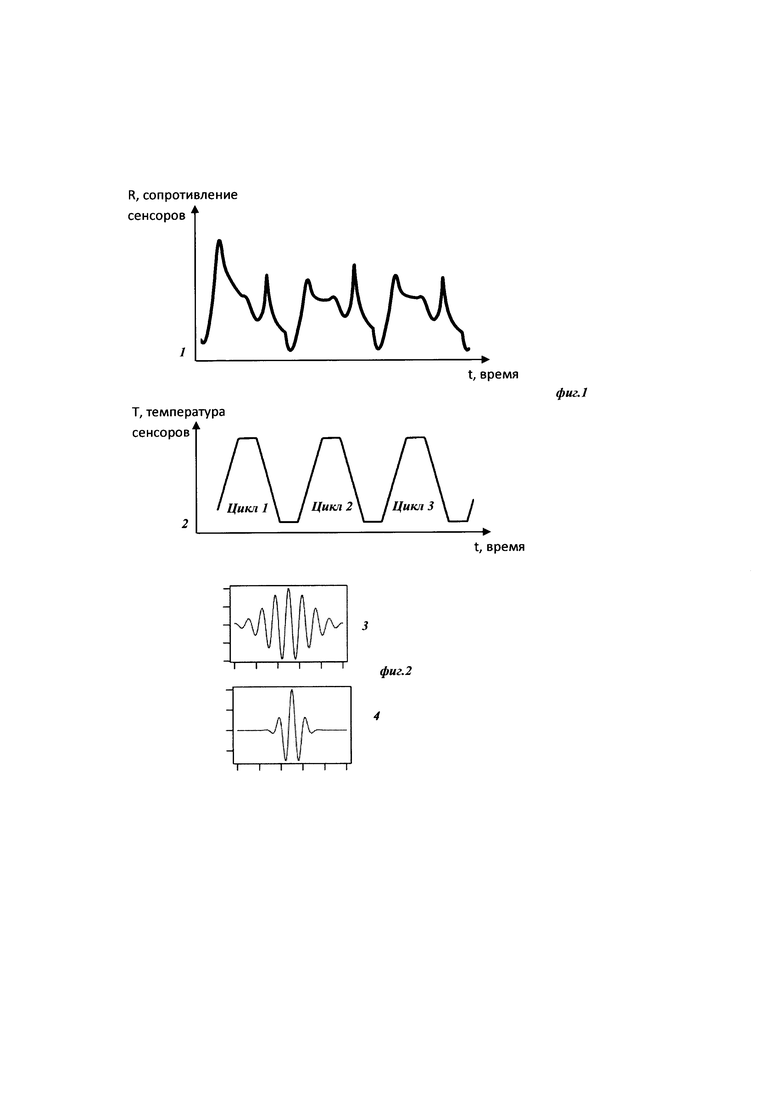
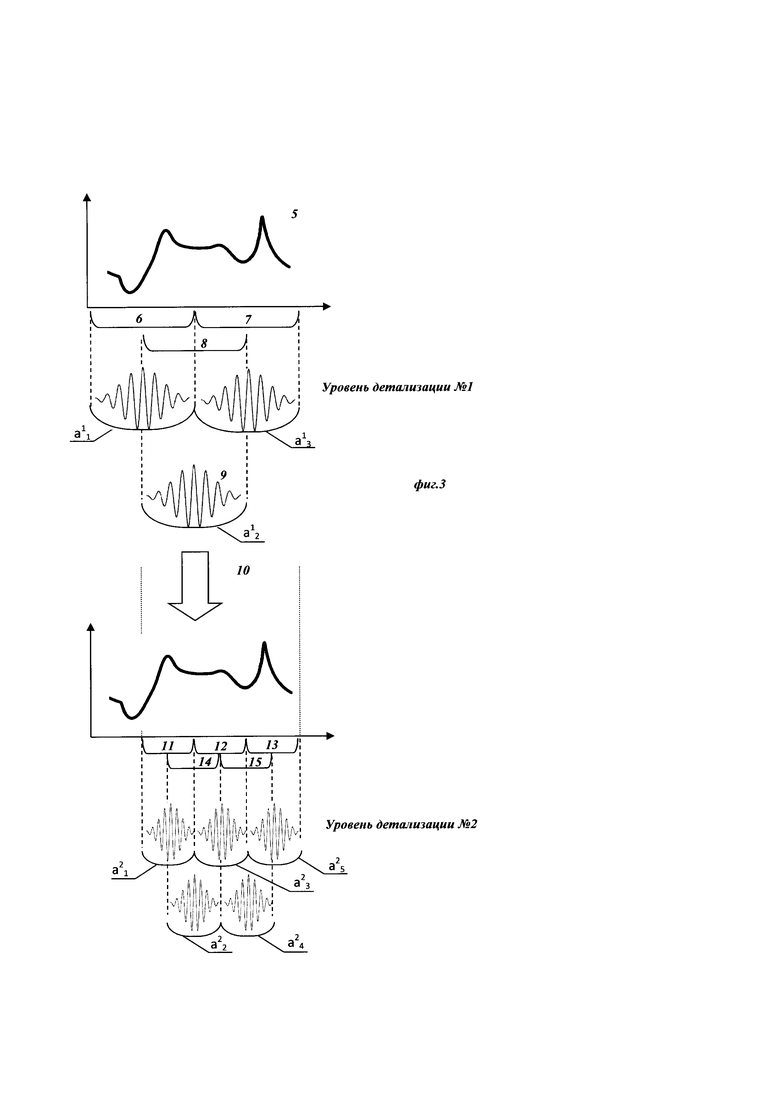
Изобретение поясняется чертежами, где на фиг. 1 представлен вид непрерывного исходного сигнала сопротивления газовых сенсоров при концентрации СО 20 ppm на протяжении 3x циклов измерений, полученного при реализации примера конкретного выполнения посредством заявляемого способа. Позициями на фигуре обозначены 1 - непрерывный сигнал сопротивления; 2 - непрерывный сигнал термометра, отражающий контролируемое изменение температуры сенсоров на протяжении нескольких циклов измерений. На фиг. 2 представлен вид вейвлет-функции Морле в зависимости от параметра центральной частоты. Вейвлет-функция в позиции 3 на данной фигуре имеет в 2.5 раза меньшее значение центральной частоты, чем изображенная в позиции 4. На фиг. 3 представлено графическое изображение двух итераций предлагаемого способа. На позиции 5 изображен пример предобработанного образца исходного сигнала, из которого выделены области, представленные позициями 6, 7 и 8, после чего производят свертку с вейвлет-функцией, представленной в позиции 9, результатом чего являются переменные а11, а12, а13. Стрелка, обозначенная позицией 10, изображает описанную процедуру отбора информативных диапазонов сигнала, после чего выбранные участки (в данном примере, позиции 7, 8) дробятся в соответствии с параметром масштаба уровня детализации 2, покрывая сигнал окнами, изображенными в позициях 11, 12, 13, 14, 15, после чего процедуру повторяют со сверткой, в результате чего получают массив переменных а21, а22, а23, а24, а25, которые могут быть использованы в последующей процедуре отбора до сходимости алгоритма.
Осуществление изобретения
Ниже представлено более детальное описание осуществления заявляемого способа, которое предназначено для пояснения сущности заявляемого изобретения. Настоящее изобретение может подвергаться различным изменениям и модификациям, понятным специалисту на основе прочтения приведенного описания. Такие изменения не ограничивают объем притязаний. Например, могут изменяться типы целевых показателей, может изменяться критерий сходимости расчета, объем исходных данных для проведения расчетов, абсолютные значения заранее заданных параметров и т.д. Способ не ограничен каким-либо классом вейвлет-функций или алгоритмом обучения, а также размерностью входных данных.
Согласно способу на первом этапе (А) осуществляют предобработку измеренного сигнала с целью удаления шума и амплитудных скачков сигнала, которая может быть реализована различными методами, известными из уровня техники: например, вычитания пьедестала [Steven W. Smith. The Scientist and Engineer's Guide to Digital Signal Processing. - Second Edition. - San-Diego: California Technical Publishing, 1999], устранения локального дрейфа полиномами малых порядков [A. Gallant and W. Fuller. Fitting segmented polynomial regression models whose join points have to be estimated. Journal of the American Statistical Association, 68(341):144-147, 1973]; ограничения выбросов, путем ограничения допустимой амплитуды скачков локальной производной, фильтрация высокочастотного шума с помощью сглаживающих фильтров, таких как скользящее среднее или медианный фильтр [Steven W. Smith. The Scientist and Engineer's Guide to Digital Signal Processing. - Second Edition. - San-Diego: California Technical Publishing, 1999], а также частотных фильтров [Britton С. Rorabaugh. Approximation Methods for Electronic Filter Design. - New York: McGraw-Hill, 1999.], позволяющих устранить высокочастотный шум и медленные осцилляции, связанные с дрейфом базовой линии.
После удаления из сигнала шума и амплитудных скачков производят разделение непрерывного сигнала на отдельные образцы равной длины, в рамках циклов, как показано в примере на фиг. 1. Общий массив примеров-образцов сигнала разделяют на 3 набора: тренировочный, вылидационный и тестовый. Классической рекомендацией для этой процедуры является разделение набора случайным образом в соотношении 70:20:10 соответственно [Т. Hastie, R. Tibshirani, J. Friedman, The Elements of Statistical Learning, Springer-Verlag New York, 745 p. 2009], однако ее конечной целью является обеспечение представительности наборов данных [Li D-C, Hu SC, Lin L-S, Yeh C-W Detecting representative data and generating synthetic samples to improve learning accuracy with unbalanced data sets. PLoS ONE 12(8): e0181853, 2017], каждый из которых должен содержать такие образцы, чтобы целевой параметр внутри наборов лежал в рамках общих границ. Дополнительным фактором, обеспечивающим объективную оценку точности решения задачи, является подход к умышленному формированию наборов из образцов данных, полученных в рамках экспериментов, независимых от тех, чьи образцы были включены в тренировочную выборку. Такой подход исключает зависимость системы от общих условий проведения эксперимента (влажность, атмосферное давление и т.п.), а также временных особенностей поведения измерительного оборудования («старение» сенсорного материала, внешние наводки измерительной электроцепи и т.п.).
На следующем этапе (Б) каждому образцу сопоставляют целевой параметр. Пример, приведенный в рамках данного описания, касается определения типов и концентраций газов в смеси, включает часть, связанную с классификацией (определением типа газа), характеризующейся узким набором дискретных значений, и части, связанной с регрессией (определением концентрации газа), характеризующейся некоторой непрерывной сеткой значений в рамках установленных границ минимального и максимального значения. Для определения типов и концентраций газов строят статистическую модель, что сводится к минимизации целевой функции, вид которой зависит от определяемого искомого параметра - является он качественным или количественным. Так, для задачи определения количественного целевого параметра (представляющего из себя непрерывный набор значений, задача регрессии) предпочтительно использование значения среднеквадратичного отклонения [Т. Hastie, R. Tibshirani, J. Friedman, The Elements of Statistical Learning, Springer-Verlag New York, 745 p. 2009], тогда как для определения качественного целевого параметра (представляющего из себя одно из нескольких детерминированных значений целевого параметра, задача классификации) предпочтительно использование так называемой функции softmax. При выборе целевых функций необходимо, чтобы функции удовлетворяли требованию дифференцируемости для случаев, когда предполагается использовать алгоритм градиентного спуска при обучении моделей [Bishop, С.М. Pattern Recognition and Machine Learning. - Springer, 2006. - 738 p].
На следующем этапе (В) выбирают семейства вейвлет-функций. Стандартные требования к вейвлет-функциям (локализованность, нулевое среднее и пр. [Charles K. Chui. An Introduction to Wavelets, Volume 1 (Wavelet Analysis and Its Applications) 1 st Edition. Academic Press, 266 p. 1992] дополняют требованием дифференцируемости для обеспечения возможности применения алгоритма градиентного спуска при обучении моделей. Отличительной особенностью заявляемого способа является отсутствие необходимости проведения обратного преобразования из пространства вейвлет-коэффициентов в исходное пространство, что снимает требование к ортогональности вейвлет-функций и становится возможным одновременное использование вейвлет-функций различных семейств вейвлетов. Пример вейвлет-функции: вейвлет Морле 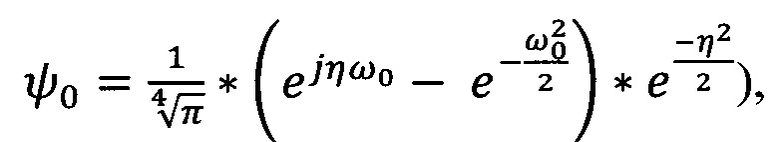 где ω0 - центральная частота вейвлета, j - мнимая единица, η - условное обозначение положения точки на оси в пространственном домене.
где ω0 - центральная частота вейвлета, j - мнимая единица, η - условное обозначение положения точки на оси в пространственном домене.
После выбора вейвлет функций задают начальные параметры - центральные частоты выбранных вейвлетов, значение масштаба и степень перекрытия соседних окон. Значение перекрытия вейвлет-окон выбирают не менее 30%, предпочтительным является 50% перекрытие вейвлет-окон. Масштаб первого уровня выбирают порядка половины числа отсчетов образца сигналов, чтобы в результате преобразования получилось несколько вейвлет-коэффициентов, как изображено в верхней части фиг. 3.
Вейвлет-преобразование можно осуществлять напрямую, при этом наиболее эффективным является использование алгоритма проведения операции свертки в Фурье-пространстве [Hramov, А.Е., Koronovskii, А.А., Makarov, V.A., Pavlov, A.N., Sitnikova, E. Wavelets in Neuroscience. Springer-Verlag Berlin Heidelberg, 318 p. 2015], например, с использованием имеющихся на рынке программных продуктов, реализующих алгоритм Фурье-преобразования [https://software.intel.com/en-us/mkl/features/fft, https://developer.nvidia.com/cufft, https://www.xilinx.com/products/intellectual-property/fft.html]. В рамках выбранного алгоритма получают Фурье-образы образцов сигналов и вейвлет-функции, после чего производят их свертку и проделывают обратное Фурье-преобразование, чтобы вернуться в исходное пространство. Результатом данного шага является набор вейвлет-коэффициентов - по одному коэффициенту для каждого окна.
На следующем этапе реализации изобретения (Г) после определения вейвлет-коэффициентов проводят построение семейства моделей, отображающих подаваемый набор коэффициентов на значения целевого параметра. Семейство содержит модели, осуществляющие преобразование входных переменных с помощью опорной функции, каждая модель внутри семейства содержит свой уникальный набор переменных. Таким образом, семейство состоит из моделей, получающих на вход все возможные комбинации входных переменных, среди которых будут отобраны лучшие на основании значения внешнего критерия, рассчитанного на валидационном наборе. Поскольку при большом количестве переменных количество моделей, которые потребуется обучить на данном шаге равно n!, то количество входных переменных ограничивают сверху, для уменьшения числа моделей до 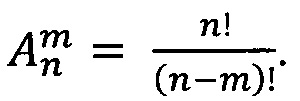 В качестве опорной функции рекомендуется использовать линейную функцию, однако возможно применение и полиномиальных функций и универсальных аппроксиматоров функций, например, радиальных базисных функций [Schwenker, Friedhelm; Kestler, Hans A.; Palm,
В качестве опорной функции рекомендуется использовать линейную функцию, однако возможно применение и полиномиальных функций и универсальных аппроксиматоров функций, например, радиальных базисных функций [Schwenker, Friedhelm; Kestler, Hans A.; Palm,  Three learning phases for radial-basis-function networks. Neural Networks. 14: 439-458. 2001] и искусственных нейронных сетей [Simon Haykin. Neural Networks: A Comprehensive Foundation (2nd ed.). Upper Saddle River, NJ: Prentice Hall. 842 p. 1999].
Three learning phases for radial-basis-function networks. Neural Networks. 14: 439-458. 2001] и искусственных нейронных сетей [Simon Haykin. Neural Networks: A Comprehensive Foundation (2nd ed.). Upper Saddle River, NJ: Prentice Hall. 842 p. 1999].
На следующем этапе (Д) для сокращения объема требуемых вычислений проводят обучение простых функций с помощью метода наименьших квадратов, однако для обучения сложных адаптивных моделей возможно использование модифицированных алгоритмов градиентного спуска [Caglar Gulcehre, Jose Sotelo, Marcin Moczulski, Yoshua Bengio. A Robust Adaptive Stochastic Gradient Method for Deep Learning. arXiv:1703.00788], которые позволяют обучать модель до приемлемого уровня за небольшое количество итераций. После окончания процедуры обучения моделей на тренировочном наборе производят оценку работы моделей на валидационном наборе, составленном из образцов, не участвовавших в процессе обучения моделей. После чего отбирают заданное число моделей, продемонстрировавших лучшие результаты, и проводят проверку оценки их эффективности на тестовом наборе данных, образцы которых не были задействованы ни в обучении, ни в выборе моделей. Если наблюдают улучшение точности определения целевого параметра на тестовом наборе (Е), в сравнении с результатами, полученными на предыдущих уровнях детализации, то области сигнала, соответствующие этим моделям, объявляют наиболее значимыми для данного уровня детализации (Ж). Если же улучшение точности определения целевого параметра на тестовом наборе не наблюдается или уровень детализации достиг значений уровня дискретизации сигналов (т.е. не представляется возможным выбрать окно меньшей ширины), то не переходят на следующий уровень детализации.
Если переходят к следующему уровню детализации на следующем этапе заявляемого способа (З), то выбирают новое значение параметра масштаба, предпочтительно двукратно меньше того, что использовалось на предыдущем уровне детализации и изменяют значение центральной частоты вейвлета для сохранения его формы в новом масштабе и далее размещают эти окна в выбранных на предыдущем шаге областях сигнала, рассчитывают вейвлет-коэффициенты (И) и далее повторяют пункты В.-И.
Пример осуществления изобретения
Для демонстрации эффективности разработанного подхода был проведен цикл измерений состава воздуха с помощью полупроводниковых газовых сенсоров производства SGX Sensortech (Швейцария). Сенсоры работали в непрерывном режиме, частота дискретизации сигнала составляла 0.1 сек, при этом было реализовано циклическое изменение их температуры, как показано на фиг. 1. Для уменьшения скачкообразности показаний сенсоров и плавности реакции ПИД управляющей системы были введены области термостабилизации на крайних значениях температуры, которую изменяли от 150 до 450 градусов цельсия со скоростью 15 градусов в секунду, длина каждой области стационарной температуры - 10 сек. Перед началом каждого эксперимента проводили продувку сенсоров уличным воздухом в течение одного часа. Измерения для заданного типа газа осуществляли по 2 часа, прерывая их получасовыми продувками установки уличным воздухом. Одна серия экспериментов включала не более трех серий измерений, после чего производили часовую продувку уличным воздухом и отключали измерительную установку. Последовательные серии экспериментов проводили на разных типов газов для исключения влияния фактора «старения» сенсорного материала на измеряемый сигнал. Эксперименты проводили с угарным газом (СО), водородом (Н2), смесью этих двух газов, уличным воздухом, а также уличным воздухом с контролируемым уровнем влажности. Газы СО и Н2 подавались из подключенных к установке баллонов, смешиваясь с нагнетаемым уличным воздухом; изменение их концентрации проводилось путем регулировки потока газа, выходящего из баллона. Концентрации менялись в диапазонах от 7 до 126 ppm (points per million) и 33 до 540 ppm для СО и Н2, соответственно, в рамках равномерной сетки из 9 значений. В тренировочный набор были включены образцы из 3x экспериментов для каждого типа газа, в валидационный - образцы из других двух экспериментов, в тестовый - из одного эксперимента.
Этап А был реализован проведением процедур, направленных на улучшение качества сигнала - очищение от шума производилось с помощью медианного фильтра шириной 8 отсчетов, устранение дрейфа базовой линии сенсоров проводилось путем устранения локальных трендов полиномами не выше третьего порядка. Каждый образец сигнала был составлен из вектора измеряемых значений сопротивления цикла нагревание-стабилизация-охлаждение-стабилизация - всего 600 отсчетов. Для устранения влияния абсолютной амплитуды сенсорного ответа образцы нормировались на собственное интегральное значение. Каждому образцу поставили в соответствие известный тип газа (качественная характеристика) и количественное (концентрация газа, для газов СО, Н2 и их смеси) (этап Б).
В качестве вейвлет-функции на этапе В был выбран вейвлет Морле, при расчете вейвлет-коэффициентов использовали только действительную часть, мнимые значения отбрасывали. Начальное значение центральной частоты выбирали 2*π3/2 что обеспечило 5 циклов синусоиды внутри выбранного масштаба. Значение параметра масштаба выбрали 200 точек, степень перекрытия соседних вейвлет-окон - 50%. Расчет вейвлетов-коэффициентов проводили в рамках осуществления свертки в Фурье-пространстве с предварительным Фурье-преобразованием образцов сигнала и вейвлет-функции и обратным преобразованием результата. Таким образом, для каждого выбранного окна на образце сигнала рассчитали по одному вейвлет-коэффициенту.
После того как были рассчитаны вейвлет-коэффициенты на них было построено семейство линейных моделей (этап Г), включающих все возможные комбинации переменных. Подбор коэффициентов моделей осуществляли методом наименьших квадратов на образцах сигнала тренировочного набора. Глобальное ограничение на количество переменных в модели составило 12, ограничение на минимально возможный размер окна - 8 отсчетов. На данном этапе проводили решение задачи классификации, кодирование желаемого значения проводили методом one-hot encoding, т.е. при наличии 4 различных значений целевого параметра (газовых сущностей): СО, Н2, смесь СО и Н2, уличный воздух, желаемое значение кодировали вектором из четырех значений, 3 из которых были равны нулю, а одно из них - единице, что соответствовало отсутствию или наличию газа. Задача регрессии была решена сходным образом с тем отличием, что выходные значения представлялись в виде массива непрерывно меняющихся значений внутри указанных диапазонов концентраций. Средняя абсолютная ошибка определения концентраций на тестовом наборе образцов составила менее 10% относительного значения концентрации.
В результате для данного уровня построили 120 моделей, после чего их точность работы оценили на валидационном наборе (этап Д). По данному критерию выбрали 25% лучших моделей. Поскольку это первый шаг, то проверку работы на тестовой выборке не проводили (этап Е). Таким образом, выбрали уникальные вейвлет-коэффициенты отобранных моделей и соответствующие им области объявили существенными для решения задачи (этап Ж).
Выбранные на шаге Ж области сигнала использовали на следующем уровне детализации (этап З), характеризующемся размером окна, вдвое меньшим, чем на предыдущем шаге, а центральная частота была увеличена в 4/3 раз для сохранения количества периодов синусоиды вейвлета Морле внутри окна. Сохраняя ту же степень перекрытия, выбрирали положения окон на образцах сигналов внутри выбранных областей и далее повторяли действия по п. В.-З.
Для технической реализации вычислительного алгоритма использовали компьютер на базе процессора intel 6600k, видеокарта nvidia gtx 1060gb, 32gb ram на базе операционной системы linux. Использование графического ускорителя и библиотеки tensorflow языка python позволили ускорить вычисления фурье-преобразования и организовать многопоточные вычисления.
Таким образом, преимущество разработанного подхода было продемонстрировано в возможности решения как задачи определения типа газа, так и определения концентраций отдельных газов и их смеси. По сравнению с известным способом по патенту US 8064722 B1, заявляемый способ, помимо возможности определения типа газа (качественного целевого параметра), позволяет определять концентрацию исследуемых газов (количественного целевого параметра), а также обеспечивает высокую точность определения целевого параметра (качественного или количественного) с выделением значимых разномасштабных областей измеряемого сигнала.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОБРАБОТКИ ВЕКТОРНЫХ СИГНАЛОВ ДЛЯ РАСПОЗНАВАНИЯ ОБРАЗОВ НА ОСНОВЕ НЕЙРОННЫХ СЕТЕЙ С ДЕТЕКТИРОВАНИЕМ ВЫБРОСОВ | 2024 |
|
RU2830154C1 |
| СПОСОБ И СИСТЕМА КОНЕЧНОГО АВТОМАТА ДЛЯ РАСПОЗНАВАНИЯ РАБОЧЕГО СОСТОЯНИЯ СЕНСОРА | 2018 |
|
RU2744908C1 |
| СПОСОБ ФОРМИРОВАНИЯ СИСТЕМЫ УПРАВЛЕНИЯ МОЗГ-КОМПЬЮТЕР | 2019 |
|
RU2704497C1 |
| СПОСОБ И СИСТЕМА АВТОМАТИЧЕСКОГО АНАЛИЗА ЭКГ | 2020 |
|
RU2767157C2 |
| Способ анализа медицинских данных с помощью нейронной сети LogNNet | 2021 |
|
RU2754723C1 |
| Способ диагностики рака легкого по анализу выдыхаемого пациентом воздуха на основе анализа биоэлектрических потенциалов обонятельного анализатора крысы | 2017 |
|
RU2666873C1 |
| СПОСОБ НЕЙРОСЕТЕВОГО ПРОГНОЗИРОВАНИЯ ИЗМЕНЕНИЯ ЗНАЧЕНИЙ ФУНКЦИИ С ЕЁ ПРЕДВАРИТЕЛЬНОЙ ВЕЙВЛЕТ-ОБРАБОТКОЙ И УСТРОЙСТВО ЕГО ОСУЩЕСТВЛЕНИЯ | 2015 |
|
RU2600099C1 |
| Способ обнаружения аномального трафика в сети | 2023 |
|
RU2811840C1 |
| КЛАССИФИКАЦИЯ САЙТОВ СПЛАЙСИНГА НА ОСНОВЕ ГЛУБОКОГО ОБУЧЕНИЯ | 2018 |
|
RU2780442C2 |
| Способ биогибридного скрининга рака легкого, рака желудка, сахарного диабета и туберкулеза легких по выдыхаемому обследуемым воздуху | 2022 |
|
RU2797334C1 |
Изобретение относится к способам обработки данных. Способ включает: A) первичную обработку сигнала x(t), нормирование предобработанного сигнала с получением массива образцов сигнала для формирования обучающей выборки, разделенной на тренировочный, валидационный и тестовый набор; Б) для каждого образца массива выборки определяют окна текущего уровня детализации (ОТУД), соответствующие заданным значением параметров ширины s и положения их центров - t, с обеспечением перекрытия соседних окон; B) каждый образец массива выборки обрабатывают с помощью вейвлет-преобразования; Г) выбирают опорную функцию, максимальное количество ее переменных с последующим построением семейства моделей для отображения с помощью выбранной функции вейвлет-коэффициентов (a1…an) на одно целевое значение; Д) после чего каждую модель из семейства по п. Г) обучают на тренировочном наборе с подбором весовых параметров моделей w1…wn и последующим выбором лучших моделей по критерию, рассчитанному на валидационном наборе; Е) проверку выбранных моделей на шаге Г) на тестовой выборке путем расчета критерия оценки сходимости алгоритма; Ж) выбор значимых участков (ЗУ), соответствующих окнам данного уровня детализации, З) переход к следующему уровню детализации внутри выбранных по п. Ж) ЗУ - ОТУД, соответствующих лучшим моделям, содержащим вейвлет-коэффициенты ai, ранее рассчитанным внутри этих окон; И) для каждого окна участков, определенных на первом уровне детализации, применяют соответствующее вейвлет-преобразование с меньшим параметром масштаба с получением детализированного представления набора ЗУ, после чего этапы В)-И) повторяют до достижения критерия сходимости, определяемого по значению целевой функции на тестовом наборе, в результате чего получают набор парных комбинаций s и t, соответствующих ЗУ измеренного сигнала, по которым определяют искомый целевой параметр. Технический результат заключается в повышении точности определения целевого параметра. 16 з.п. ф-лы, 3 ил.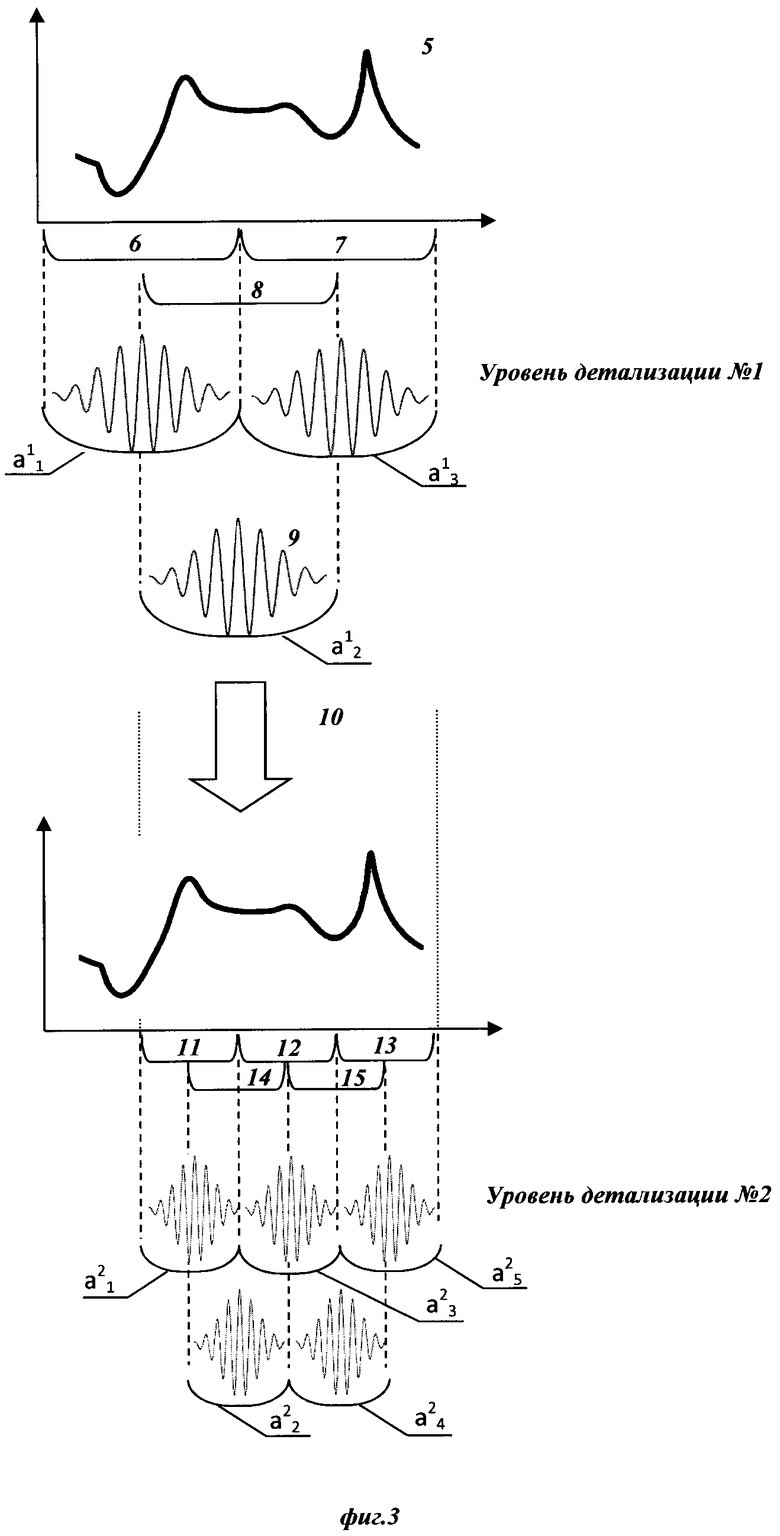
1. Способ обработки векторных сигналов для распознавания образов на основе вейвлет-анализа, включающий
A) первичную обработку измеренного одномерного сигнала x(t) посредством удаления высокочастотного шума с последующим нормированием предобработанного сигнала с получением массива образцов измеренного сигнала для формирования обучающей выборки, разделенной на тренировочный, валидационный и тестовый набор, где каждому образцу измеренного сигнала сопоставляют известное значение по меньшей мере одного целевого параметра;
Б) для каждого образца из полученного массива обучающей выборки определяют окна текущего уровня детализации, соответствующие заданным значением параметров ширины s и положения их центров - t, с обеспечением перекрытия соседних окон;
B) каждый образец из полученного массива обучающей выборки обрабатывают с помощью вейвлет-преобразования с осуществлением свертки вейвлет-функции по перекрывающимся окнам данного уровня детализации с получением вейвлет-коэффициентов (a1…аn);
Г) выбирают опорную функцию, максимальное количество ее переменных с последующим построением семейства моделей для отображения с помощью выбранной функции вейвлет-коэффициентов (a1…аn) на по меньшей мере одно целевое значение;
Д) после чего каждую модель из семейства по п. Г) обучают на тренировочном наборе с подбором весовых параметров моделей w1…wn и последующим выбором лучших моделей по критерию, рассчитанному на валидационном наборе;
Е) проверку выбранных моделей на шаге Г) на тестовой выборке путем расчета критерия оценки сходимости алгоритма;
Ж) выбор значимых участков, соответствующих окнам данного уровня детализации,
З) переход к следующему уровню детализации внутри выбранных по п. Ж) значимых участков - окон текущего уровня детализации, соответствующих лучшим моделям, содержащим вейвлет-коэффициенты аi, ранее рассчитанным внутри этих окон;
И) для каждого окна из значимых участков, определенных на первом уровне детализации, применяют соответствующее вейвлет-преобразование с меньшим параметром масштаба с получением детализированного представления набора значимых участков, после чего этапы В) - И) повторяют до достижения критерия сходимости, определяемого по значению целевой функции на тестовом наборе, в результате чего получают набор парных комбинаций s и t, соответствующих значимым участкам измеренного сигнала, по которым определяют искомый целевой параметр.
2. Способ по п. 1, характеризующийся тем, что в качестве одномерного сигнала x(t) используют значения, непрерывно получаемые с измерительного оборудования.
3. Способ по п. 1, характеризующийся тем, что высокочастотный шум удаляют с использованием медианного фильтра.
4. Способ по п. 1, характеризующийся тем, что нормирование предобработанного сигнала осуществляют посредством деления значений сигнала в каждой точке на интегральное значение измеренного сигнала.
5. Способ по п. 1, характеризующийся тем, что образцы массива измеренного сигнала выбирают одинаковой длины.
6. Способ по п. 1, характеризующийся тем, каждый из наборов массива образцов измеренного сигнала - тренировочного, тестового и валидационного, формируют из подмножества образцов измерений, полученных в ходе экспериментов, проведенных в разное время.
7. Способ по п. 1, характеризующийся тем, что в качестве целевого параметра используют количественный или качественный параметр.
8. Способ по п. 1, характеризующийся тем, что вейвлет-преобразовние представляет собой
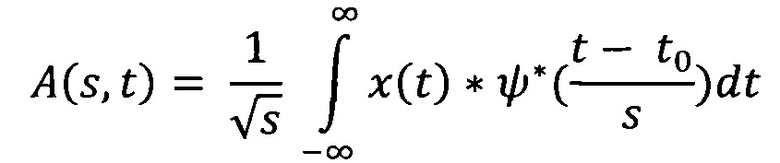 ,
,
где x(t) - исходный сигнал, ψ* - комплексно-сопряженная материнская вейвлет-функция.
9. Способ по п. 1, характеризующийся тем, что в качестве вейвлет-функции используют функции, удовлетворяющие следующим свойствам: локализации; нулевого среднего; ограниченности; дифференцируемости; самоподобия.
10. Способ по п. 1, характеризующийся тем, что перекрытие соседних окон составляет не менее 30% от ширины окна.
11. Способ по п. 1, характеризующийся тем, что свертку сигнала с вейвлет-функцией осуществляют в фурье-пространстве, для чего: вычисляют Фурье-образ дискретных сигналов, представляющих из себя последовательности значений {хn}:
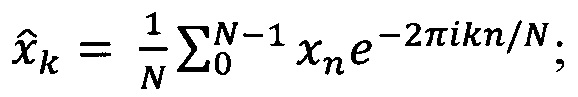
вычисляют Фурье-образ вейвлет-функции:
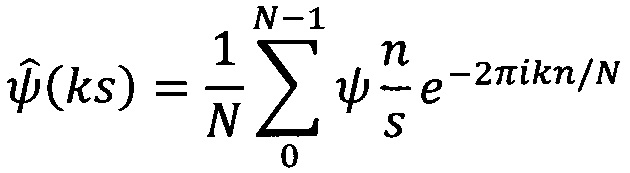 ,
,
умножают Фурье-образ дискретных сигналов на комплексно-сопряженный Фурье-образ вейвлет-функции и производят обратное Фурье-преобразование:
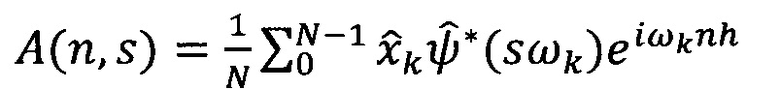 ;
;
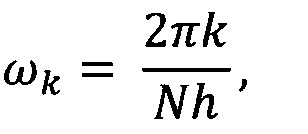
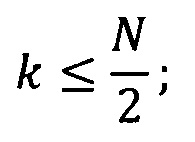
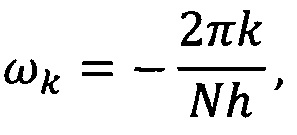
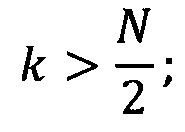
где n - 0, 1, …, N-1, N - число отсчетов в исследуемом ряду данных; h - интервал между последовательными отсчетами временного домена, k/h ⊂ (0, …, (N-1)/h) образует множество частот исходного сигнала хn.
12. Способ по п. 1, характеризующийся тем, что в качестве опорной функции выбирают
линейную функцию, состоящую из членов нулевого и первого порядка:
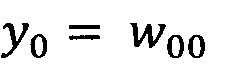
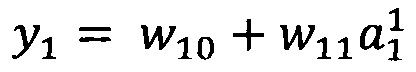
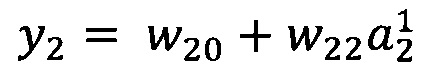
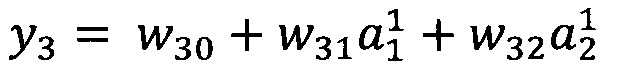
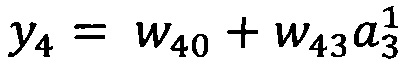
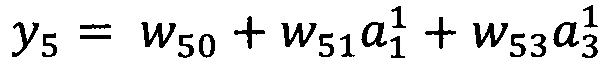
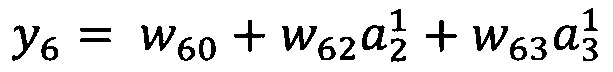
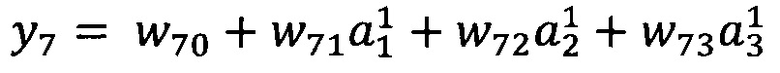 .
.
13. Способ по п. 1, характеризующийся тем, что обучение проводят посредством минимизации внутреннего критерия - суммы квадратов регрессионных остатков на тренировочном наборе:
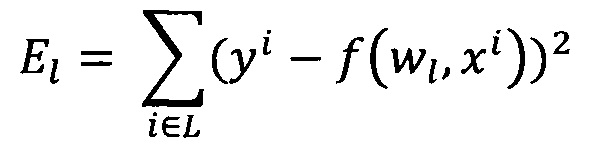 .
.
14. Способ по п. 13, характеризующийся тем, что минимизацию внутреннего критерия осуществляют с помощью алгоритма наименьших квадратов:
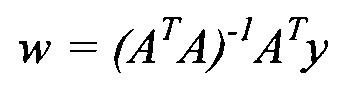 .
.
15. Способ по п. 1, характеризующийся тем, что выбор лучших моделей осуществляют на основе внешнего критерия, рассчитанного на валидационном наборе, - суммы квадратов регрессионных остатков моделей, построенных на тренировочном наборе, с нормировкой на соответствующие целевые значения:
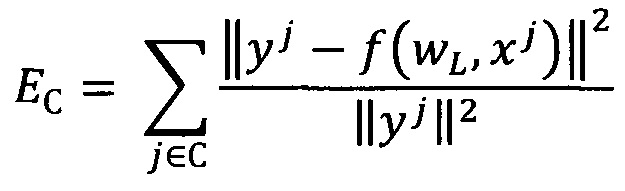 .
.
16. Способ по п. 1, характеризующийся тем, что из построенного семейства моделей выбирают четвертую часть моделей, являющихся лучшими по оценке внешнего критерия на валидационном наборе.
17. Способ по п. 1, характеризующийся тем, что переход к следующему уровню детализации осуществляют лишь в том случае, если точность определения целевого параметра на тестовом наборе для хотя бы одной из отобранных моделей превзошла результаты, полученные на предыдущем уровне детализации.
| US 8064722 B1, 22.11.2011 | |||
| US 2016161448 A1, 09.06.2016 | |||
| Сакрутина Е | |||
| А., Бахтадзе Н | |||
| Н | |||
| ИДЕНТИФИКАЦИЯ СИСТЕМ НА ОСНОВЕ ВЕЙВЛЕТ-АНАЛИЗА, доклад на 12-м Всероссийском совещании по проблемам управления, Москва, 2014 | |||
| US 8595164 B2, 26.11.2013. |
Авторы
Даты
2019-05-30—Публикация
2017-12-29—Подача