Изобретение относится к области вычислительной техники и может быть использовано для определения параметров ориентации множества лучей лазерного подсвета относительно системы координат видеокамеры. Способ предполагается использовать в системах технического зрения, которые состоят из конструктивно жестко закрепленных камеры и устройства многолучевого лазерного подсвета и предназначены для измерения расстояния до объектов наблюдаемой сцены.
Из уровня техники известны процедуры калибровки для определения взаимного расположения стереокамеры и трехмерного сканирующего лазерного дальномера (Абраменко А.А. Калибровка взаимного расположения стереокамеры и трехмерного сканирующего лазерного дальномера // Компьютерная оптика. 2019. Т. 43, №2. С. 220-230) и калибровки системы видеокамер и лидаров автономных мобильных комплексов (Блохинов Ю.Б., Андриенко Е.Э., Казахмедов К.К., Вишняков Б.В. Автоматическая калибровка системы видеокамер и лидаров для автономных мобильных комплексов // Компьютерная оптика. 2021. Т. 45, №3. С. 382-393). В данных процедурах применяются плоские тест-объекты с ArUco-маркерами. Данные маркеры представляют собой специальным образом закодированные метки (Garrido-Jurado S, Muñoz-Salinas R., Madrid-Cuevas F., Marín-Jiménez M. Automatic generation and detection of highly reliable fiducial markers under occlusion // Pattern Recognition. 2014. Vol. 47, Is. 6. P. 2280-2292; Romero-Ramirez F., Munoz-Salinas R., Medina-Carnicer R. Speeded up detection of squared fiducial markers // Image and Vision Computing. 2018. Vol. 76. P. 38-47), каждая из которых имеет свой индивидуальный номер и свою систему координат.
Процедура детектирования углов тест-объекта с нанесенными на него ArUco-маркерами в облаке точек измерений лидара состоит из следующих основных этапов:
1) детектирование светоотражающих меток;
2) кластеризация пространства на основе евклидова расстояния и выделение граничных точек;
3) получение уравнений пространственных прямых, на которых лежат граничные точки;
4) вычисление положений углов тест-объекта как точек пересечения прямых из шага 3).
Процедура детектирования углов тест-объекта с нанесенными на него ArUco-маркерами на изображении камеры содержит следующие основные этапы:
1) детектирование и уточнение углов ArUco-маркеров: выполняется с помощью функций библиотеки обработки изображений OpenCV, которые детектируют маркеры и возвращают набор их углов и соответствующий каждому маркеру индекс;
2) поиск и уточнение границ стенда: выполняется с помощью детектора границ Кэнни (Canny J.A. Computational approach to edge detection // IEEE Trans, on Pattern Analysis and Machine Intelligence. 1986. Vol. 8, Is. 6. P. 679-698);
3) вычисление положений углов стенда как точек пересечения прямых линий, описывающих его границы;
4) расчет отступов для параллельного переноса прямых, найденных на шаге 3), с использованием информации о линейных размерах ArUco-маркера.
Поскольку координаты углов тест-объектов в системе координат тест-объекта априорно известны, то, зная также координаты углов в системах координат как камеры, так и лидара, для их систем координат вычисляют матрицы поворота Rкам и Rлид, а также векторы параллельного переноса tкам и tлид относительно системы координат тест-объекта по методу наименьших квадратов (Umeyama S. Least-squares estimation of transformation parameters between two point patterns // IEEE Trans, on Pattern Analysis and Machine Intelligence. 1991. Vol. 13, Is. 4. P. 376-380).
Недостатком процедур калибровки является тот факт, что при детектировании углов тест-объекта в облаке точек с лидара применяется алгоритм кластеризации пространства. Данный этап необходим ввиду требования о наличии некоторой дистанции между тест-объектом и иными объектами сцены во время калибровки, поскольку аналитически нельзя отделить стоящие вплотную друг к другу объекты с прямолинейными границами. Поскольку плотность точек измерений лидара не столь высока, как плотность пикселей на изображении с камеры, то такая кластеризация позволяет выделить границы тест-объекта, а, следовательно, и его угловые точки только приближенно.
Известен алгоритм калибровки лидара и камеры по тест-объекту в форме плоского щита с круглым отверстием априорно известного радиуса (Fremont V., Rodriguez Florez S.A., Bonnifait P. Circular targets for 3D alignment of video and lidar sensors // Advanced Robotics. 2012. Vol. 26. P. 2087-2113). Путем автоматического выделения контура отверстия на изображении предварительно откалиброванной камеры (с известной матрицей внутренних параметров) и в облаке точек лидара для различных ракурсов съемки тест-объекта получают наборы соответствий пространственных координат центра отверстия тест-объекта в системе координат камеры и лидара. Это позволяет оценить внешние параметры: матрицу поворота R и вектор параллельного переноса t.
Недостатком алгоритма также является погрешность оценки параметров центра тест-объекта из-за низкой плотности облака точек лидара.
На применении плоского тест-объекта с отверстием известного радиуса также основан и способ калибровки стереопары и лидара, применяемый в подсистеме формирования 3D видео с круговым полем зрения для системы виртуальной реальности (патент US 9872010 В2, опубликовано 16.01.2018, МПК: H04N 13/02 (2006.01), G06T5/50 (2006.01)). При этом для калибровки используется всего два положения такого тест-объекта, снятых на различных удалениях от стереопары и лидара: условно ближнем и дальнем.
Система и способ калибровки камеры и лидара (патент CN112840232, опубликовано 25.05.2021, МПК: G06T 7/80(2006.01)) также основаны на съемке тест-объекта с двух дистанций, причем вторая из них больше, чем первая. При этом тест-объект представляет собой плоскую пластину с фиксированным расположением на ней отверстий априорно известной формы: квадратов, упорядоченных в шахматном порядке, или массива круглых отверстий с априори известным расстоянием между их центрами, или любую их комбинацию.
В системе и способе для калибровки лидара и камеры (патент US 10726579 В1, опубликовано 28.07.2020, МПК: H04N7/18 (2006.01), H04N 17/00 (2006.01), G06T7/80 (2017.01), G01S 7/497 (2006.01), G01S 17/42 (2006.01), G01S 17/86 (2020.01), G05D 1/02 (2020.01)) выполняется съемка калибровочного объекта, представляющего собой стандартный планарный шаблон для калибровки камер с нанесенным на него изображением типа «шахматное поле» (Zhang Z. A flexible new technique for camera calibration // IEEE Transactions on Pattern Analysis and Machine Intelligence. 2000. Vol. 22(11). P. 1330-1334). В данном способе системой калибровки принимается множество кадров с данными об облаках точек от лидара, которые включают в себя шаблон калибровки, и множество изображений, которые также включают в себя шаблон калибровки. Система калибровки вычисляет первую нормаль к плоскости калибровочного шаблона в первом кадре с облаком точек лидара и дополнительно вычисляет вторую нормаль к плоскости калибровочного шаблона в первом кадре изображения с камеры из принятого множества изображений. Система калибровки вычисляет параметры евклидова преобразования (поворот, параллельный перенос) между извлеченной первой нормалью и извлеченной второй нормалью и на основе вычисленного преобразования реализует калибровку лидара с камерой. Учет нормалей, вычисленных таким образом, по множеству снятых с различных ракурсов кадров с изображением калибровочного шаблона от камеры и лидара позволяет уменьшить ошибку оценивания параметров евклидова преобразования.
В системе и способе калибровки сенсоров системы датчиков (патент US 10962630 В1, опубликовано 30.03,2021, МПК: G06T7/80 (2017.01), G01S 7/497 (2006.01)) для оценивания параметров евклидова преобразования применения тест-объекта не требуется: поиск соответствий между пикселями изображения с камеры и точками облака измерений лидара основан на автоматическом выделении границ. В указанном способе калибровки датчиков получают двухмерное изображение от первого датчика (камеры), получают данные трехмерного облака точек от второго датчика (лидара), определяют (с помощью оператора Собела) области двумерного изображения, на которых имеются наиболее выраженные границы, вдоль которых наблюдается перепад яркости, и проецируют границы трехмерного облака точек данных на выделенные границы двумерного изображения. При этом вводят множество гипотез относительно возможных евклидовых преобразований между границей трехмерного облака точек и границей двумерного изображения, причем для множества преобразований вводят вероятности того, что пиксель границы двухмерного изображения соответствует точке границы трехмерного облака точек. Затем с помощью метода оптимизации ветвей и границ путем итеративной оценки из множества евклидовых преобразований определяют преобразование с наименьшей функцией штрафа, причем для преобразования с наименьшим штрафом обеспечивается наибольшая вероятность того, что пиксель границы двухмерного изображения соответствует точке границы трехмерного облака точек. При этом способ калибровки оперирует функцией штрафа, которая позволяет максимизировать вероятность соответствия границ на изображении и в облаке точек лидара.
Известен способ калибровки камеры и лидара для формирования карт высокого разрешения (патент US 10897575 В2, опубликовано 19,01.2021, МПК: H04N5/00 (2011.01), G06T 7/00 (2017.01)). Данный способ предполагает наличие тест-объекта, которым выступает планарный калибровочный шит с нанесенным на его поверхность шаблоном типа «шахматное поле» или «цветные прямоугольники». Координаты углов тест-объекта в системе координат камеры находят из решения задачи Perspective-n-Point (Fischler М.А., Bolles R.C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography // Communications of the ACM. 1981. Vol. 24, No. 6. P. 381-395), где точками с априорно известными координатами являются автоматически детектируемые на изображении углы квадратов или прямоугольников шаблона, нанесенного на тест-объект, поскольку отступы углов изображений шаблона от углов тест-объекта априорно известны. Координаты углов тест-объекта в системе координат лидара находят путем сегментации облака точек лидара. Процедура калибровки в способе прототипа заключается в том, что система «камера-лидар» формирует массив снимков тест-объекта с различных ракурсов и расстояний. На данных снимках автоматически определяют координаты углов тест-объекта в системах координат камеры и лидара. Далее выполняют репроекцию вычисленных по информации от лидарного облака точек пространственных координат углов тест-объекта на изображение с камеры для каждого ракурса съемки и итеративно с помощью численного алгоритма оптимизации уточняют параметры, связывающие системы координат камеры и лидара - матрицу поворота и вектор параллельного переноса. Как указано в описании прототипа, алгоритмом оптимизации может выступать, например, алгоритм Левенберга - Марквардта. Итерации повторяют до тех пор, пока не будет достигнут локальный минимум суммы квадратов ошибок репроекций. Соответствующие данному условию матрицу поворота и вектор параллельного переноса и принимают за искомые значения.
Для калибровки согласно данному способу необходимо, чтобы угловое расстояние между соседними лазерными лучами было малым и составляло не более чем доли градуса: в описании способа указано, что точки лазерного подсвета, расположенные на одной линии сканирования, находятся на угловом расстоянии Δϕ=0,2°.
Известен способ калибровки лидара и видеодатчиков (патент US 10436884 В2, опубликовано 08.10.2019, МПК: H04N7/18 (2006.01), G01S 7/497 (2006.01)). Реализуемый в данном изобретении способ калибровки по меньшей мере лазерного блока и блока машинного зрения, оба из которых установлены на общей мобильной платформе, включает:
- объединение упорядоченных во времени наборов информации о точках, полученных от лазерного устройства, для формирования облака точек в системе отсчета, связанной с мобильной платформой, на основе одного или нескольких правил преобразования, при этом одно или несколько правил преобразования определяют преобразования между системами отсчета, связанными с лазером блок в разные моменты времени в пределах периода времени для целевой системы отсчета, связанной с лазерным блоком, в целевой момент времени;
- извлечение множества характерных точек соответствий из облака точек, при этом характерные точки соответствуют пороговому разрыву при измерении глубины;
- оценку характерных точек соответствий с помощью информации о контурах изображений, полученной от блока машинного зрения, на основе целевой функции, причем указанная целевая функция определяется, по меньшей мере, положениями характерных точек соответствий при проецировании на систему отсчета, связанную с блоком машинного зрения;
генерирование по меньшей мере одного правила калибровки для калибровки между лазерным блоком и блоком технического зрения на основе, по меньшей мере, оценки характерных точек с помощью информации о контурах;
- выполнение калибровки между лазерным блоком и блоком машинного зрения с использованием по меньшей мере одного правила калибровки.
К недостатку рассмотренного способа следует отнести ошибки формирования пар соответствий характерных точек в условиях низкой освещенности, а также на периодических или слабо выраженных текстурах наблюдаемых объектов (Efimov A.I., Kudinov LA., Melnik O.V., Nikiforov М.В., Kholopov IS. Digital multispectral images superimposition based on preliminary calibration or contour analysis: ad-vantages and disadvantages // Proc. of ELEKTRO 2020 Conference. Taormina, Italy, 2020. P. 1-6).
В качестве прототипа выбран наиболее близкий по совокупности признаков способ взаимной калибровки видеокамеры и устройства веерного лазерного подсвета (патент RU2788666, опубликовано 24.01.2023, МПК: G06T7/80 (2017.01), G01S 7/497 (2006.01)), в котором формируют массив снимков планарного тест-объекта с различных ракурсов и расстояний, для каждого ракурса наблюдения тест-объекта определяют координаты его характерных точек в системах координат камеры и лазерного устройства, выполняют репроекцию точек с известными в системе координат лазерного устройства координатами на изображение с камеры и итеративно с помощью численного алгоритма оптимизации уточняют матрицу поворота и вектор параллельного переноса между системами координат камеры и лазерного устройства. При этом угловое расстояние между лучами устройства веерного лазерного подсвета составляет единицы градусов. В способе прототипа измеряют пространственные координаты проекций точек лазерного подсвета на плоскость тест-объекта в системе координат тест-объекта, вычисляют линейные расстояния между данными точками в каждой строке и в каждом столбце сетки проекций, по теореме косинусов составляют переопределенную относительно неизвестных расстояний от устройства лазерного подсвета до проекций точек подсвета систему нелинейных уравнений, решают ее численным методом и вычисляют пространственные координаты проекций точек подсвета на плоскость тест-объекта в системе координат устройства веерного лазерного подсвета.
К недостаткам способа прототипа следует отнести:
- необходимость итеративного численного решения переопределенной системы нелинейных уравнений;
- необходимость выполнять маркировку центров проекций лазерных лучей на поверхности тест-объекта вручную и измерять линейные расстояния между ними.
Техническая проблема, решаемая созданием заявленного изобретения, заключается в необходимости ручной маркировки точек проекций лучей лазерного подсвета на плоскости тест-объекта и ручного измерения их координат в системе координат тест-объекта, что исключает автоматизацию процедуры калибровки способа прототипа.
Технический результат изобретения заключается в автоматизации измерений необходимых для калибровки пространственных координат точек проекций лучей лазерного подсвета на плоскости тест-объекта.
Технический результат достигается следующим образом.
Как и в способе патента US 10726579 В1, в качестве тест-объекта в предлагаемом способе применяется планарный калибровочный шаблон типа «шахматное поле». Первоначально выполняется съемка N1≥15 кадров такого тест-объекта с различных ракурсов при выключенном устройстве лазерного подсвета. Далее калибровочный шаблон ориентируется таким образом, чтобы на него на различных дальностях при каждой ориентации попадали все точки лазерного подсвета, и выполняется съемка еще 2N2 кадров, причем N2≥2. При этом в каждом положении тест-объекта регистрируют кадр с выключенным и включенным устройством лазерного подсвета. Таким образом, получают N2(1)=N2 первых кадров без лазерных точек и N2(2)=N2 вторых кадров - с точками лазерного подсвета - с аналогичным ракурсом съемки шаблона.
Затем выполняют фотограмметрическую калибровку камеры по N1+N2(1) кадрам, например, с применением методики Джанга (Zhang Z. A flexible new technique for camera calibration // IEEE Transactions on Pattern Analysis and Machine Intelligence. 2000. Vol. 22(11). P. 1330-1334). По результатам калибровки получают оценки элементов матрицы внутренних параметров камеры K и элементов вектора коэффициентов дисторсии ее оптической системы согласно модели Брауна - Конради (Brown D.C. Close-range camera calibration // Photogrammetric Engineering. 1971. Vol. 37, No. 8. P. 855-866).
В процессе калибровки промежуточно вычисляют матрицы поворота и векторы параллельного переноса ti, i=1…N1+N2(1), для перехода от системы координат видеокамеры ОкамXкамYкамZкам к системам координат тест-объектов OTO(i)XTO(i)YTO(i)ZTO(i) и векторы параметров πi=[nxi, nyi, nzi, di]T, задающие уравнения их плоскостей в пространстве:
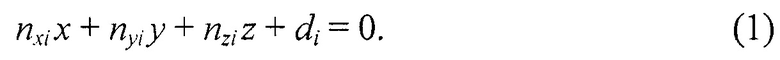
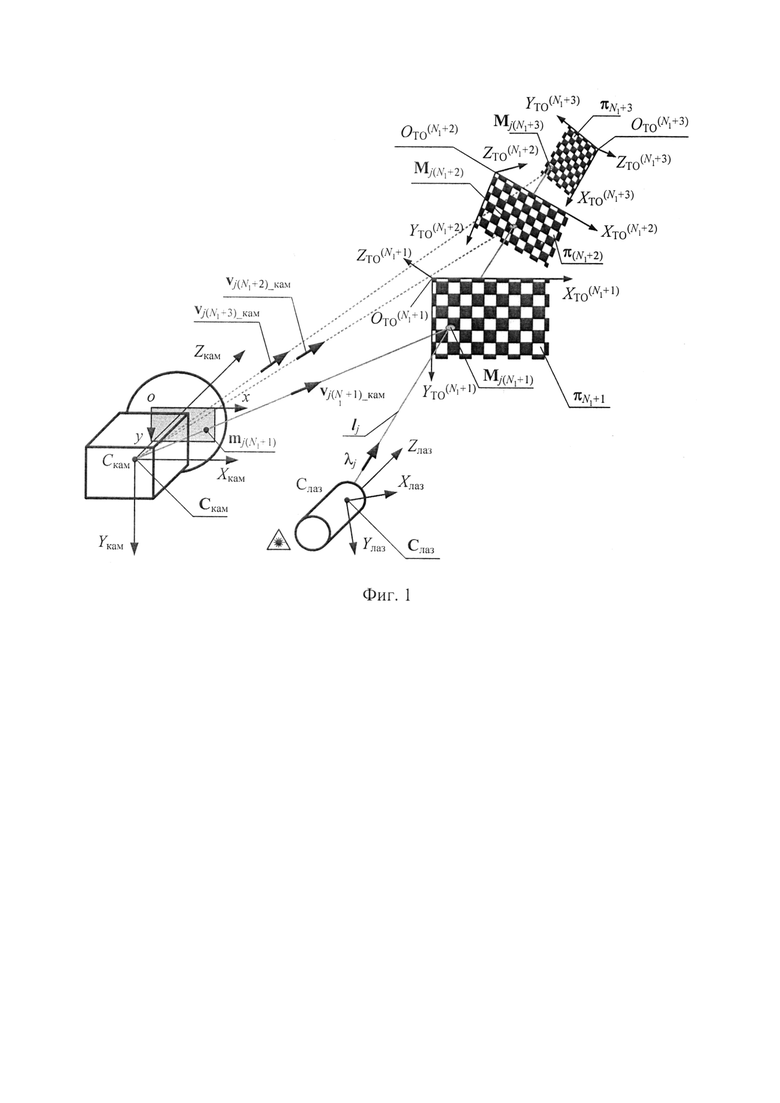
Далее на каждом из N2(2) вторых кадров выделяют с субпиксельной точностью однородные пиксельные координаты всех точек проекций лучей лазерного подсвета mjk, где j - номер луча лазерного подсвета j=1, 2, …, Nn, где k=N1+1, N1+2, … N1+N2(2), a Nл - количество лучей лазерного подсвета. Для наглядности, но без нарушения общности рассматриваемой задачи, на фиг. 1 геометрическая постановка задачи взаимной калибровки видеокамеры и устройства многолучевого лазерного подсвета рассмотрена всего для одного, j-го, луча подсвета и N2(2)=3. Для оценивания координат центров изображений точек подсвета с субпиксельной точностью применяют один из известных из уровня техники способов: например, с помощью двухпороговой или средневзвешенной обработки (Шадрин М.В. Лазерный триангуляционный 3D метод и устройство для прототипирования и изготовления сложных изделий: дис. канд. техн. наук. Рязань, 2020).
Автоматизировать процесс перемещения тест-объекта относительно видеокамеры позволяет, например, применение систем и устройств для выполнения автоматизированной фото- и видеограмметрической калибровки (патент RU2645432, опубликовано 21.02.2018, МПК: G01C 11/00 (2006.01); патент RU2749363, опубликовано 09.06.2021, МПК: G06T7/80 (2017.01)).
Затем полученные однородные пиксельные координаты нормируют,

и с применением одного из численных методов минимизации, например, Гаусса - Ньютона, Левенберга - Марквардта или Нелдера - Мида, выполняют компенсацию дисторсии. В результате получают нормированные однородные координаты mjk_норм* без дисторсии.
Далее формируют направляющие векторы для каждой точки mjk_норм* в системе координат видеокамеры
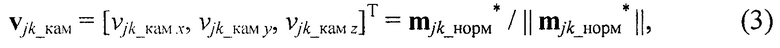
где 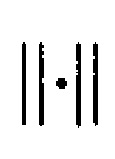 - оператор вычисления два-нормы вектора.
- оператор вычисления два-нормы вектора.
Направляющие векторы (3) позволяют вычислить пространственные координаты точек Mjk пересечения прямых, проходящих через точку начала системы координат камеры Скам, с плоскостями πk
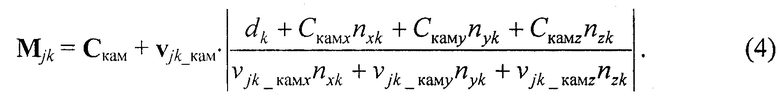
При выборе системы координат камеры в качестве основной, т.е. Скам=[Скамх, Скаму, Скамz]T=[0, 0, 0]T, выражения (4) упрощается:
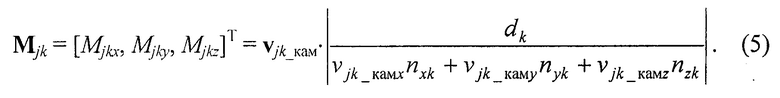
По рассчитанным пространственным координатам далее вычисляют направляющие векторы λj=[λjx, λjу, λjz]T прямых lj, вдоль которых дисперсия множества точек {Mjk}, k=N1+2, … N1+N2(2), минимальна. Указанные векторы могут быть вычислены, например, с помощью разложения по сингулярным числам (singular value decomposition, SVD) матрицы CovjTCovj, где Covj - ковариационная матрица для множества {Mjk},
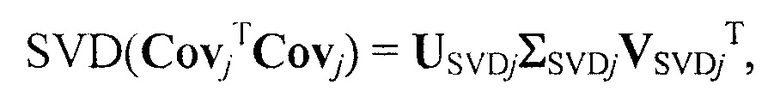
где ΣSVDj - диагональная матрица упорядоченных по убыванию сингулярных чисел, a USVDj и VSVDj - унитарные матрицы, состоящие из левых и правых сингулярных векторов соответственно.
В этом случае векторы λj являются соответствующими минимальным сингулярным числам ΣSVD_minj векторами матриц VSVDj.
Затем для каждой пары скрещивающихся прямых {lj, ip) с направляющими векторами λj и λр соответственно, j, р=1, 2, …, Nл, j≠р, соответствующих j-му и р-му лучам подсвета, вычисляют координаты точки Cjp середины отрезка минимальной длины, перпендикулярного обеим прямым (Виро О.Я., Дроботухина Ю.В. Конфигурации скрещивающихся прямых // Алгебра и анализ. 1989. Т. 1. Вып. 4. С. 222-246). Для этого составляют матрицу Djp и вектор djp такие, что
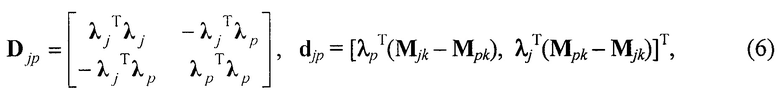
вычисляют весовые множители

точки Cj и Cp, лежащие на данных прямых,
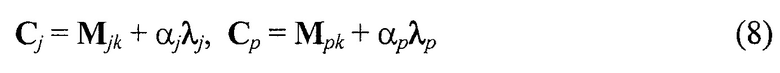
и координаты центра отрезка
Cip=0,5(Cj+Ср).
За пространственные координаты точки Слаз начала системы координат устройства многолучевого лазерного подсвета в системе координат камеры принимают математическое ожидание множества точек {Cjp}
Слаз=М{Cjp},
где М{⋅} - оператор оценки математического ожидания.
Информация о направляющих векторах λj и координатах точки Слаз в системе координат камеры и является результатом калибровки, поскольку указанные параметры позволяют восстановить пространственные координаты точки Mj, на которую падает j-й луч подсвета. Действительно, если оценены пиксельные координаты mj центра изображения точки подсвета и вычислен направляющий вектор vj на данную точку по (3), то по аналогии с (6)-(8) пространственные координаты Mj определяются посредством следующих вычислений:
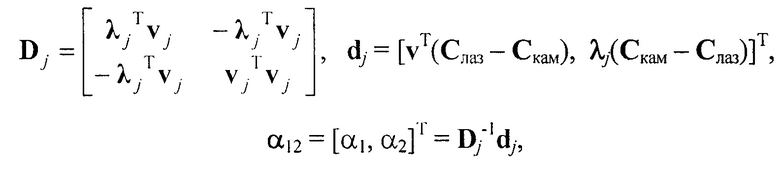
C1=Слаз+α1λj, C2=Скам+α2V,
Mj=0,5(C1+C2).
Таким образом, полученные в результате калибровки ансамбль направляющих векторов лучей подсвета {λj} и пространственные координаты точки начала системы координат устройства многолучевого подсвета Слаз обеспечивают восстановление пространственных координат измерительным устройством, состоящим из видеокамеры и устройства многолучевого лазерного подсвета.
Изобретение относится к вычислительной технике. Технический результат заключается в автоматизации измерений необходимых для калибровки пространственных координат точек проекций лучей лазерного подсвета на плоскости тест-объекта. На этапах способа: формируют массив снимков планарного тест-объекта с различных ракурсов и расстояний, определяют координаты точек тест-объекта в системах координат камеры и лазерного устройства; измеряют пространственные координаты проекций точек веерного лазерного подсвета на плоскость тест-объекта в системе координат тест-объекта; в каждой строке и в каждом столбце сетки проекций вычисляют линейные расстояния между данными точками, вычисляют пространственные координаты проекций точек подсвета на плоскость тест-объекта в системе координат устройства подсвета; выполняют репроекцию точек с известными пространственными координатами на изображение с камеры для каждого ракурса и итеративно уточняют матрицу поворота и вектор параллельного переноса между системами координат камеры и устройства веерного лазерного подсвета. 1 ил.
1. Способ взаимной калибровки видеокамеры и устройства многолучевого лазерного подсвета, в котором формируют массив снимков планарного тест-объекта с различных ракурсов и расстояний, для каждого ракурса наблюдения определяют координаты характерных точек тест-объекта в системе координат камеры, получают пространственные координаты проекций точек лазерного подсвета на плоскости тест-объекта в системе координат тест-объекта, отличающийся тем, что с помощью устройства для автоматизированной фото- и видеограмметрической калибровки снимают N1 кадров калибровочного шаблона при выключенном устройстве лазерного подсвета и первые и вторые N2 кадров - при попеременно выключенном и включенном устройстве подсвета в каждом положении тест-объекта соответственно, при этом в ходе съемки вторых N2 кадров с включенным устройством подсвета, причем N2≥2, тест-объект ориентируют таким образом, чтобы на него попадали все точки лазерного подсвета, получают направляющие векторы λj прямых lj, проходящих через точки проекций каждого j-го луча подсвета на плоскость тест-объекта, находят для каждой пары скрещивающихся прямых lj и lp, соответствующих j-му и р-му лучам подсвета, пространственные координаты точек Cjp, являющихся центрами отрезков минимальной длины, перпендикулярных обеим прямым lj и lp, и вычисляют координаты точки Слаз начала системы координат устройства многолучевого лазерного подсвета в системе координат видеокамеры как математическое ожидание множества точек {Cjp}.
| СПОСОБ ВЗАИМНОЙ КАЛИБРОВКИ ВИДЕОКАМЕРЫ И УСТРОЙСТВА ВЕЕРНОГО ЛАЗЕРНОГО ПОДСВЕТА | 2021 |
|
RU2788666C1 |
| US 10726579 B1, 28.07.2020 | |||
| CN 118033605 A, 14.05.2024 | |||
| CN 113050074 A, 29.06.2021 | |||
| CN 110021046 A, 16.07.2019 | |||
| АБРАМЕНКО А.А | |||
| "Калибровка взаимного расположения стереокамеры и трёхмерного сканирующего лазерного дальномера ", Компьютерная оптика, том 43, 2, опубл | |||
| Станок для придания концам круглых радиаторных трубок шестигранного сечения | 1924 |
|
SU2019A1 |
Авторы
Даты
2025-05-19—Публикация
2024-06-06—Подача