Изобретение относится к области вычислительной техники и может быть использовано для определения внешних параметров камеры - матрицы поворота и векторного параллельного переноса ее системы координат относительно системы координат устройства веерного лазерного подсвета. Способ предполагается использовать в системах технического зрения, которые состоят из конструктивно жестко закрепленных камеры и устройства веерного лазерного подсвета и предназначены для измерения расстояния до объектов наблюдаемой сцены.
Из уровня техники известны процедуры калибровки для определения взаимного расположения стереокамеры и трехмерного сканирующего лазерного дальномера (Абраменко А.А. Калибровка взаимного расположения стереокамеры и трехмерного сканирующего лазерного дальномера // Компьютерная оптика. 2019. Т. 43, №2. С.220-230) и калибровки системы видеокамер и лидаров автономных мобильных комплексов (Блохинов Ю.Б., Андриенко Е.Э., Казахмедов К.К., Вишняков Б.В. Автоматическая калибровка системы видеокамер и лидаров для автономных мобильных комплексов // Компьютерная оптика. 2021. Т. 45, №3. С.382-393). В данных процедурах применяются плоские тест-объекты с ArUco-маркерами. Данные маркеры представляют собой специальным образом закодированные метки (Garrido-Jurado S,  R., Madrid-Cuevas F.,
R., Madrid-Cuevas F.,  M. Automatic generation and detection of highly reliable fiducial markers under occlusion // Pattern Recognition. 2014. Vol.47, Is. 6. P. 2280-2292; Romero-Ramirez F.,
M. Automatic generation and detection of highly reliable fiducial markers under occlusion // Pattern Recognition. 2014. Vol.47, Is. 6. P. 2280-2292; Romero-Ramirez F.,  R., Medina-Carnicer R. Speeded up detection of squared fiducial markers // Image and Vision Computing. 2018. Vol.76. P. 38-47), каждая из которых имеет свой индивидуальный номер и свою систему координат.
R., Medina-Carnicer R. Speeded up detection of squared fiducial markers // Image and Vision Computing. 2018. Vol.76. P. 38-47), каждая из которых имеет свой индивидуальный номер и свою систему координат.
Процедура детектирования углов тест-объекта с нанесенными на него ArUco-маркерами в облаке точек измерений лидара состоит из следующих основных этапов:
1) детектирование светоотражающих меток;
2) кластеризация пространства на основе евклидова расстояния и выделение граничных точек;
3) получение уравнений пространственных прямых, на которых лежат граничные точки;
4) вычисление положений углов тест-объекта как точек пересечения прямых из шага 3).
Процедура детектирования углов тест-объекта с нанесенными на него ArUco-маркерами на изображении камеры содержит следующие основные этапы:
1) детектирование и уточнение углов ArUco-маркеров: выполняется с помощью функций библиотеки обработки изображений OpenCV, которые детектируют маркеры и возвращают набор их углов и соответствующий каждому маркеру индекс;
2) поиск и уточнение границ стенда: выполняется с помощью детектора границ Кэнни (Canny J.A. Computational approach to edge detection // IEEE Trans, on Pattern Analysis and Machine Intelligence. 1986. Vol.8, Is. 6. P. 679-698);
3) вычисление положений углов стенда как точек пересечения прямых линий, описывающих его границы;
4) расчет отступов для параллельного переноса прямых, найденных на шаге 3), с использованием информации о линейных размерах ArUco-маркера.
Поскольку координаты углов тест-объектов в системе координат тест-объекта априорно известны, то, зная также координаты углов в системах координат как камеры, так и лидара, для их систем координат вычисляют матрицы поворота Rкам и Клид, а также векторы параллельного переноса tкам и tлид относительно системы координат тест-объекта по методу наименьших квадратов (Umeyama S. Least-squares estimation of transformation parameters between two point patterns // IEEE Trans, on Pattern Analysis and Machine Intelligence. 1991. Vol.13, Is. 4. P. 376-380).
Недостатком процедур калибровки является тот факт, что при детектировании углов тест-объекта в облаке точек с лидара применяется алгоритм кластеризации пространства. Данный этап необходим ввиду требования о наличии некоторой дистанции между тест-объектом и иными объектами сцены во время калибровки, поскольку аналитически нельзя отделить стоящие вплотную друг к другу объекты с прямолинейными границами. Поскольку плотность точек измерений лидара не столь высока, как плотность пикселей на изображении с камеры, то такая кластеризация позволяет выделить границы тест-объекта, а, следовательно, и его угловые точки только приближенно.
Известен алгоритм калибровки лидара и камеры по тест-объекту в форме плоского щита с круглым отверстием априорно известного радиуса (Fremont V., Rodriguez Florez S.A., Bonnifait P. Circular targets for 3D alignment of video and lidar sensors // Advanced Robotics. 2012. Vol.26. P. 2087-2113). Путем автоматического выделения контура отверстия на изображении предварительно откалиброванной камеры (с известной матрицей внутренних параметров) и в облаке точек лидара для различных ракурсов съемки тест-объекта получают наборы соответствий пространственных координат центра отверстия тест-объекта в системе координат камеры и лидара. Это позволяет оценить внешние параметры: матрицу поворота R и вектор параллельного переноса t.
Недостатком алгоритма также является погрешность оценки параметров центра тест-объекта из-за низкой плотности облака точек лидара.
На применении плоского тест-объекта с отверстием известного радиуса также основан и способ калибровки стереопары и лидара, применяемый в подсистеме формирования 3D видео с круговым полем зрения для системы виртуальной реальности (патент US 9872010 В2, опубликовано 16.01.2018, МПК: H04N 13/02 (2006.01), G06T 5/50 (2006.01)). При этом для калибровки используется всего два положения такого тест-объекта, снятых на различных удалениях от стереопары и лидара: условно ближнем и дальнем.
Система и способ калибровки камеры и лидара (патент CN112840232, опубликовано 25.05.2021, МПК: G06T 7/80(2006.01)) также основаны на съемке тест-объекта с двух дистанций, причем вторая из них больше, чем первая. При этом тест-объект представляет собой плоскую пластину с фиксированным расположением на ней отверстий априорно известной формы: квадратов, упорядоченных в шахматном порядке, или массива круглых отверстий с априори известным расстоянием между их центрами, или любую их комбинацию.
В системе и способе для калибровки лидара и камеры (патент US 10726579 В1, опубликовано 28.07.2020, МПК: H04N7/18 (2006.01), H04N 17/00 (2006.01), G06T 7/80 (2017.01), G01S 7/497 (2006.01), G01S 17/42 (2006.01), G01S 17/86 (2020.01), G05D 1/02 (2020.01)) выполняется съемка калибровочного объекта, представляющего собой стандартный планарный шаблон для калибровки камер с нанесенным на него изображением типа «шахматное поле» (Zhang Z. A flexible new technique for camera calibration // IEEE Transactions on Pattern Analysis and Machine Intelligence. 2000. Vol.22(11). P. 1330-1334). В данном способе системой калибровки принимается множество кадров с данными об облаках точек от лидара, которые включают в себя шаблон калибровки, и множество изображений, которые также включают в себя шаблон калибровки. Система калибровки вычисляет первую нормаль к плоскости калибровочного шаблона в первом кадре с облаком точек лидара и дополнительно вычисляет вторую нормаль к плоскости калибровочного шаблона в первом кадре изображения с камеры из принятого множества изображений. Система калибровки вычисляет параметры евклидова преобразования (поворот, параллельный перенос) между извлеченной первой нормалью и извлеченной второй нормалью и на основе вычисленного преобразования реализует калибровку лидара с камерой. Учет нормалей, вычисленных таким образом, по множеству снятых с различных ракурсов кадров с изображением калибровочного шаблона от камеры и лидара позволяет уменьшить ошибку оценивания параметров евклидова преобразования.
В системе и способе калибровки сенсоров системы датчиков (патент US10962630B1, опубликовано 30.03.2021, МПК: G06T 7/80 (2017.01), G01S 7/497 (2006.01)) для оценивания параметров евклидова преобразования применения тест-объекта не требуется: поиск соответствий между пикселями изображения с камеры и точками облака измерений лидара основан на автоматическом выделении границ. В указанном способе калибровки датчиков получают двухмерное изображение от первого датчика (камеры), получают данные трехмерного облака точек от второго датчика (лидара), определяют (с помощью оператора Собела) области двумерного изображения, на которых имеются наиболее выраженные границы, вдоль которых наблюдается перепад яркости, и проецируют границы трехмерного облака точек данных на выделенные границы двумерного изображения. При этом вводят множество гипотез относительно возможных евклидовых преобразований между границей трехмерного облака точек и границей двумерного изображения, причем для множества преобразований вводят вероятности того, что пиксель границы двухмерного изображения соответствует точке границы трехмерного облака точек. Затем с помощью метода оптимизации ветвей и границ путем итеративной оценки из множества евклидовых преобразований определяют преобразование с наименьшей функцией штрафа, причем для преобразования с наименьшим штрафом обеспечивается наибольшая вероятность того, что пиксель границы двухмерного изображения соответствует точке границы трехмерного облака точек. При этом способ калибровки оперирует функцией штрафа, которая позволяет максимизировать вероятность соответствия границ на изображении и в облаке точек лидара.
В качестве прототипа выбран наиболее близкий по совокупности признаков способ калибровки камеры и лидара для формирования карт высокого разрешения (патент US 10897575 В2, опубл. 19.01.2021, МПК: H04N 5/00 (2011.01), G06T 7/00 (2017.01)). Данный способ предполагает наличие тест-объекта, которым выступает планарный калибровочный щит с нанесенным на его поверхность шаблоном типа «шахматное поле» или «цветные прямоугольники». Координаты углов тест-объекта в системе координат камеры находят из решения задачи Perspective-n-Point (Fischler М.А., Bolles R.C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography // Communications of the ACM. 1981. Vol.24, No. 6. P. 381-395), где точками с априорно известными координатами являются автоматически детектируемые на изображении углы квадратов или прямоугольников шаблона, нанесенного на тест-объект, поскольку отступы углов изображений шаблона от углов тест-объекта априорно известны. Координаты углов тест-объекта в системе координат лидара находят путем сегментации облака точек лидара. Процедура калибровки в способе прототипа заключается в том, что система «камера-лидар» формирует массив снимков тест-объекта с различных ракурсов и расстояний. На данных снимках автоматически определяют координаты углов тест-объекта в системах координат камеры и лидара. Далее выполняют репроекцию вычисленных по информации от лидарного облака точек пространственных координат углов тест-объекта на изображение с камеры для каждого ракурса съемки и итеративно с помощью численного алгоритма оптимизации уточняют параметры, связывающие системы координат камеры и лидара - матрицу поворота и вектор параллельного переноса. Как указано в описании прототипа, алгоритмом оптимизации может выступать, например, алгоритм Левенберга - Марквардта. Итерации повторяют до тех пор, пока не будет достигнут локальный минимум суммы квадратов ошибок репроекций. Соответствующие данному условию матрицу поворота и вектор параллельного переноса и принимают за искомые значения.
При этом в описании способа прототипа указано, что для калибруемого лидара справедливо следующее: точки лидара, расположенные на одной линии сканирования, находятся на угловом расстоянии Δϕ=0,2°=0,0034 рад друг от друга. Поэтому на малых расстояниях от калибруемой пары «камера-лидар» на полученных облаках трехмерных точек можно определить пространственные координаты углов тест-объекта с низкой погрешностью.
Действительно, при удалении тест-объекта на дальность L абсолютная погрешность

поэтому, например, для L = 1 м погрешность ε ≈ 0,0017 м, т.е. менее 2 мм.
В то же время для ряда оптико-электронных систем, в которых требуется обработка информации от камеры и лазерного устройства, угловое расстояние между лазерными точками может быть на порядок большим, т.е. составлять уже не доли, а единицы градусов. Например, для стереосистемы с лазерным подсветом, предназначенной для построения карты глубины под летательным аппаратом в режиме маловысотного полета (Баранчиков А.И., Муратов Е.Р., Никифоров М.Б., Устюков Д.И. Обнаружение точек лазерного подсвета стереосистемы на сложном фоне // Известия ТулГУ. Технические науки. 2018. Вып.9. С.10-19), расстояние между соседними лучами веерного источника лазерного подсвета составляет Δϕ=3,75°=0,064 рад, что при подстановке в (1) дает погрешность ε ≈ 0,03 м=3 см, т.е. не позволяет при калибровке с планарными тест-объектами определять пространственные координаты их углов с погрешностью менее единиц сантиметров.
Вторым фактором, ограничивающим применение способа прототипа для оптико-электронных систем с активным лазерным подсветом, например, с веерным расположением лучей, является отсутствие дальномерной информации от лазерного канала, поскольку устройство лазерного подсвета, в отличие от лидара, не измеряет дальность до объектов, а только формирует на их поверхностях проекции своих лучей.
Техническая проблема, решаемая созданием заявленного изобретения, заключается в высокой погрешности определения с помощью тест-объектов параметров евклидова преобразования, связывающих системы координат камеры и устройства лазерного подсвета с веерным расположением лучей и угловым расстоянием между соседними лучами в единицы градусов.
Технический результат изобретения заключается в определении пространственных координат проекций точек лазерного подсвета с веерным расположением лучей с угловым расстоянием между соседними лучами в единицы градусов с абсолютной погрешностью не более единиц миллиметров, т.е. сопоставимой с аналогичной погрешностью способа прототипа, для которого угловое расстояние между лучами является на порядок меньшим.
Технический результат достигается следующим образом.
Калибровочный планарный тест-объект с отверстиями или нанесенными на него маркерами (ArUco-маркеры, шахматное поле, цветные прямоугольники и др.) не используют: вместо этого проецируют точки устройства веерного лазерного подсвета, например, лазера, перед которым установлена дифракционная решетка (Ландсберг Г.С. Оптика: учебное пособие. 7-е изд. М.: ФИЗМАТЛИТ, 2017. 852 с) на планарный тест-объект с неплоскостностью не более единиц миллиметров. Таким тест-объектом на практике может выступать, например, выровненная стена внутри помещения.
Далее вручную приближенно маркируют центры проекций лазерных лучей на поверхности тест-объекта: при линейных размерах лазерного пятна не более 1 см абсолютная погрешность маркировки центра пятна в единицы миллиметров, как показывает практика, достижима.
Затем измеряют координаты нанесенных на тест-объект маркеров Mij в системе координат тест-объекта ОTOXTOYTOZTO. Такое измерение с абсолютной погрешностью менее 1 мм возможно, например, либо посредством предварительного нанесения на поверхность тест-объекта шаблона с шагом сетки в 1 мм (например, миллиметровой бумаги), либо применением координатно-измерительной машины. Во втором случае неплоскотность тест-объекта, на который проецируются точки лазерного подсвета, может составлять и более единиц миллиметров, поскольку измерения с помощью координатно-измерительной машины позволяют оценить в том числе и координату глубины каждого маркера с погрешностью менее 1 мм (https://www.hexagonmi.com/products/portable-measuring-arms/romer-absolute-arm-compact).
Далее с использованием теоремы косинусов определяют расстояния Lij от источника лазерного подсвета до маркеров Мij по известным расстояниям между ними dij↔k и di↔k,j вдоль строки и столбца соответственно, i,j, k=[-N0,5, N0,5], i≠k, j≠k, N0,5=]N/2[, где N - количество лазерных лучей устройства подсвета по вертикали и горизонтали, ]⋅[ - оператор округления до ближайшего меньшего целого, 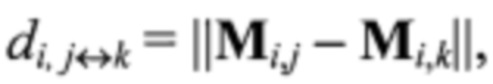 ,
, 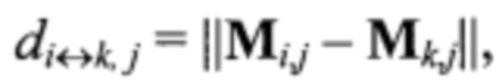 ||⋅|| - оператор вычисления евклидовой нормы вектора. При этом для составления уравнений по теореме косинусов анализируют треугольники с двумя вершинами в точках подсвета по строке или столбцу и третьей вершиной в начале системы координат устройства лазерного подсвета. Поскольку количество различных треугольников с вершинами, располагающимися в одной строке или в одном столбце точек подсвета, равно N(N-1)/2, то общее количество уравнений для всех строк и столбцов Ny=N2(N-1).
||⋅|| - оператор вычисления евклидовой нормы вектора. При этом для составления уравнений по теореме косинусов анализируют треугольники с двумя вершинами в точках подсвета по строке или столбцу и третьей вершиной в начале системы координат устройства лазерного подсвета. Поскольку количество различных треугольников с вершинами, располагающимися в одной строке или в одном столбце точек подсвета, равно N(N-1)/2, то общее количество уравнений для всех строк и столбцов Ny=N2(N-1).
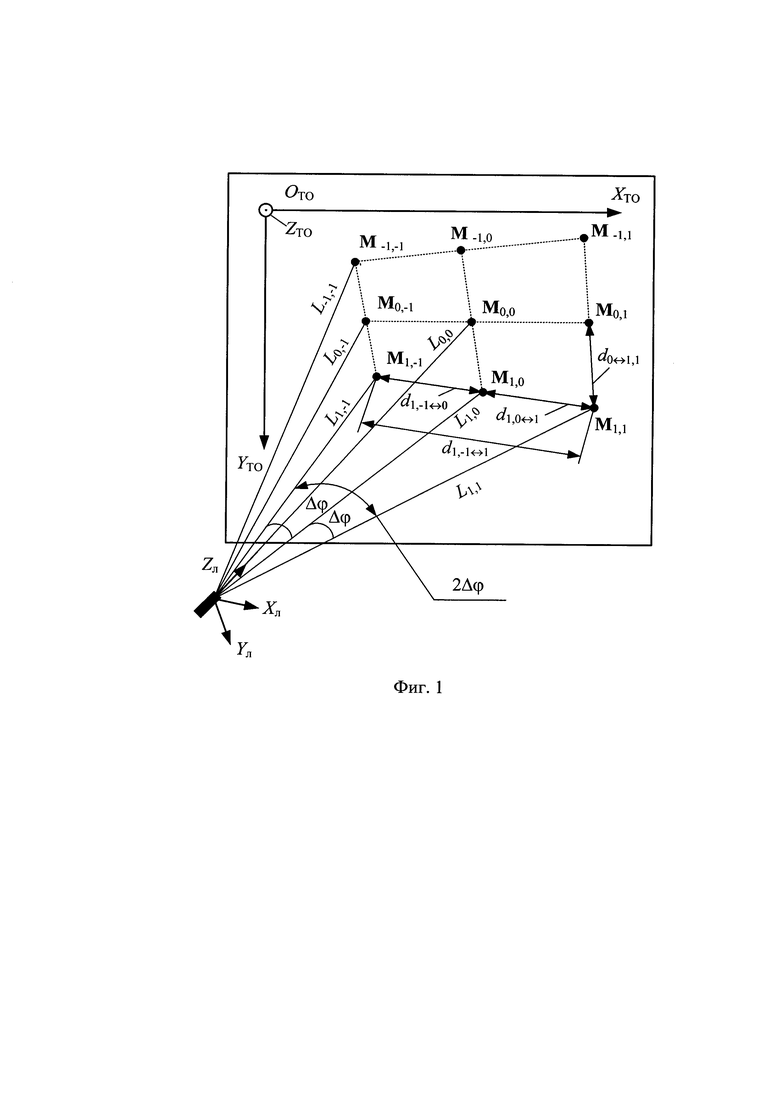
Геометрическая постановка задачи на примере c N=3 приведена на фиг. 1.
Для постановки задачи согласно фиг. 1 по теореме косинусов формируют нелинейную систему уравнений, состоящую из Ny=N2(N-1)=32⋅(3-1)=18 уравнений вида:
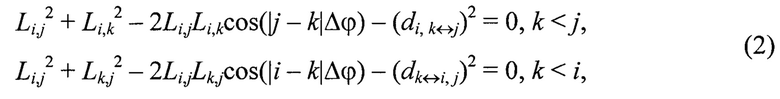
которая является переопределенной относительно неизвестных Li,j.
Псевдорешение нелинейной системы (2) находят с применением численного метода минимизации два-нормы ошибки псевдорешения, например, с помощью алгоритма Левенберга - Марквардта.
В качестве начального приближения для Li,j на первой итерации численного алгоритма оптимизации подставляют значения Li,j приближенно измеренные, например, с помощью рулетки.
Например, для геометрической постановки задачи согласно фиг. 1 переопределенная относительно вектора переменных {L-1,-1, L-1,0, L-1,1, L0,-1, L0,0, L0,1, L1,-1, L1,0, L1,1} система уравнений (2) имеет вид:
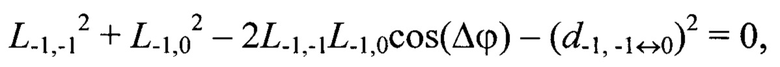
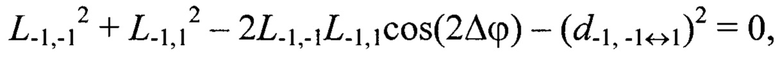
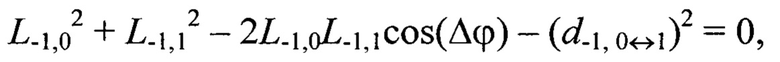
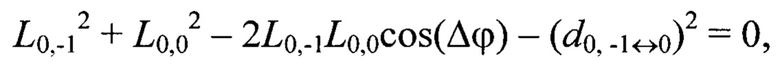
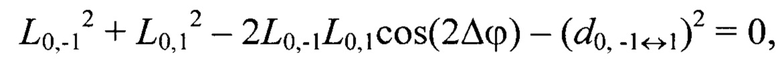
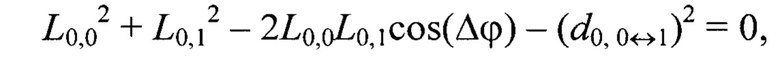
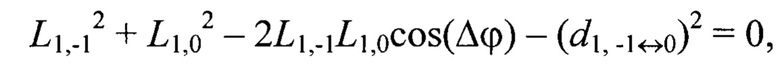
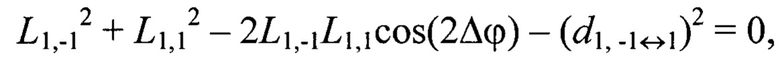
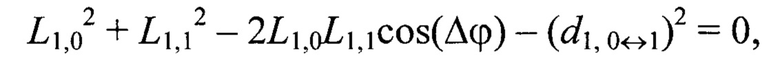
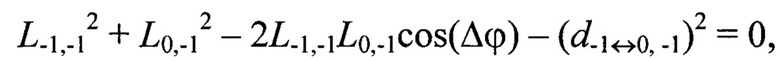
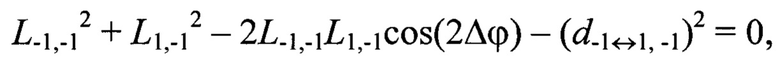
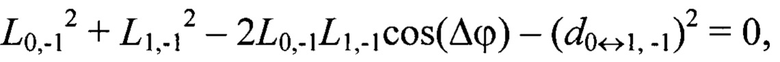
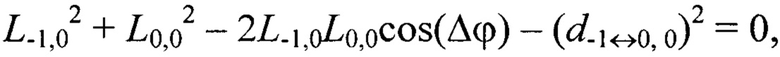
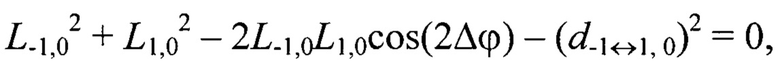
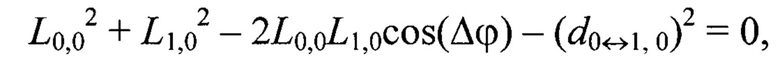
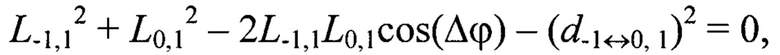
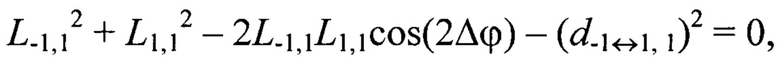
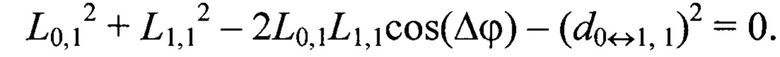
Далее по известным дальностям до маркеров Мi,j, i,j=[-N0,5, N0,5], вычисляют их пространственные координаты 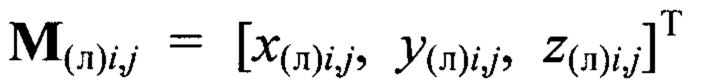 в системе координат устройства лазерного подсвета OлXлYлZл:
в системе координат устройства лазерного подсвета OлXлYлZл:
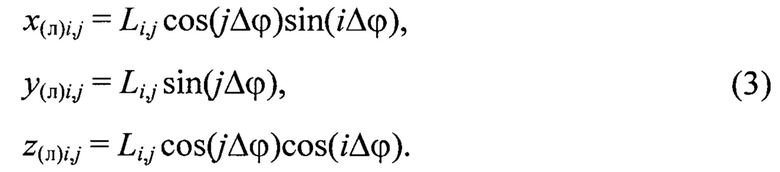
К вычисленным по (3) координатам 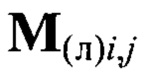 применяется операция репроецирования на плоскость изображения камеры. При этом предполагается, что матрица внутренних параметров камеры К и вектор коэффициентов дисторсии ее объектива уже априорно известны, например, получены в ходе фотограмметрической калибровки камеры по одному из известных способов (Hartley R., Zisserman A. Multiple View Geometry in Computer Vision: 2nd ed. Cambridge: Cambridge University Press, 2003. 656 p.).
применяется операция репроецирования на плоскость изображения камеры. При этом предполагается, что матрица внутренних параметров камеры К и вектор коэффициентов дисторсии ее объектива уже априорно известны, например, получены в ходе фотограмметрической калибровки камеры по одному из известных способов (Hartley R., Zisserman A. Multiple View Geometry in Computer Vision: 2nd ed. Cambridge: Cambridge University Press, 2003. 656 p.).
При искомых матрице поворота R и векторе переноса t между системами координат камеры и устройства лазерного подсвета для модели проективной камеры (при условии компенсации вносимых объективом геометрических искажений изображения по известному вектору коэффициентов дисторсии) будет выполняться условие минимума суммы квадратов ошибок репроекций:
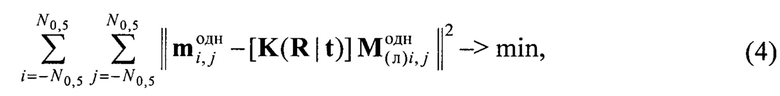
где
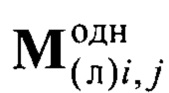 - однородные координаты маркеров
- однородные координаты маркеров 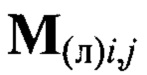 в системе координат устройства лазерного подсвета,
в системе координат устройства лазерного подсвета, 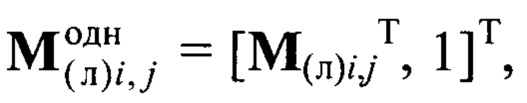
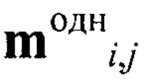 - однородные пиксельные координаты центров проекций изображений точек подсвета в плоскости изображения.
- однородные пиксельные координаты центров проекций изображений точек подсвета в плоскости изображения.
Оператор «|» в (4) обозначает операцию аугментации - пристыковки столбца к матрице справа.
Для уменьшения погрешности оценивания R и t оптимизацию по критерию минимума суммы квадратов ошибок репроекций по результатам измерений выполняют не для одного ракурса съемки тест-объекта, а для нескольких:
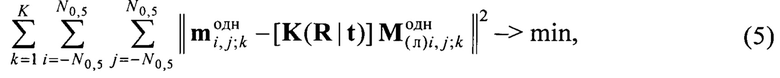
где К - количество ракурсов.
Нелинейный функционал (5) также оптимизируют с применением численного алгоритма, например, Левенберга - Марквардта.
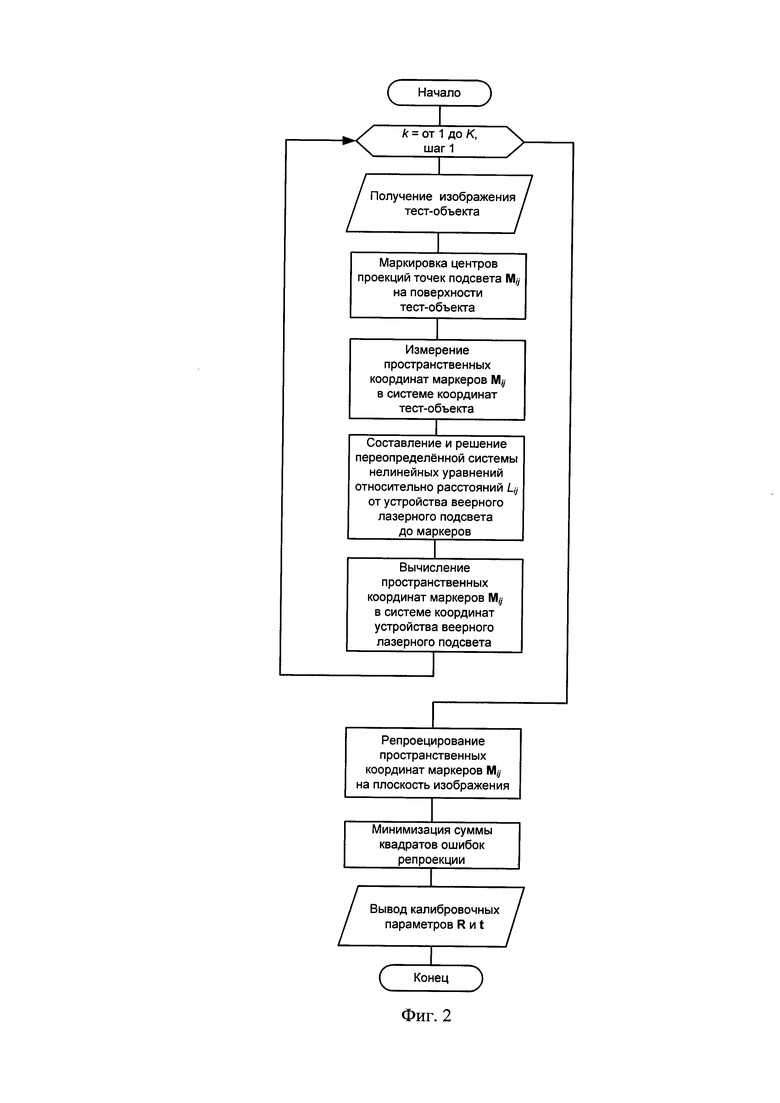
Схема алгоритма, по которому реализуют способ калибровки, приведена на фиг. 2.
Таким образом, предлагаемый способ позволяет выполнить калибровку камеры и устройства веерного лазерного подсвета, не измеряющего дальность до объектов сцены и имеющего угловое расстояние между лучами порядка единиц градусов.
Изобретение относится к способам калибровки оптических устройств. Технический результат заключается в обеспечении возможности определения пространственных координат проекций точек лазерного подсвета с веерным расположением лучей с угловым расстоянием между соседними лучами в единицы градусов с абсолютной погрешностью не более единиц миллиметров. Технический результат достигается за счет того, что формируют массив снимков планарного тест-объекта с различных ракурсов и расстояний и определяют координаты точек тест-объекта в системах координат камеры и лазерного устройства; измеряют пространственные координаты проекций точек подсвета на плоскость тест-объекта в системе координат тест-объекта, вычисляют расстояния между данными точками, составляют переопределенную относительно неизвестных расстояний систему нелинейных уравнений, решают ее и определяют пространственные координаты проекций точек подсвета на плоскость тест-объекта в системе координат подсвета; далее выполняют репроекцию точек с известными в системе координат подсвета пространственными координатами на изображение с камеры для каждого ракурса и уточняют матрицу поворота и вектор параллельного переноса между системами координат камеры и подсвета. 1 з.п. ф-лы, 2 ил.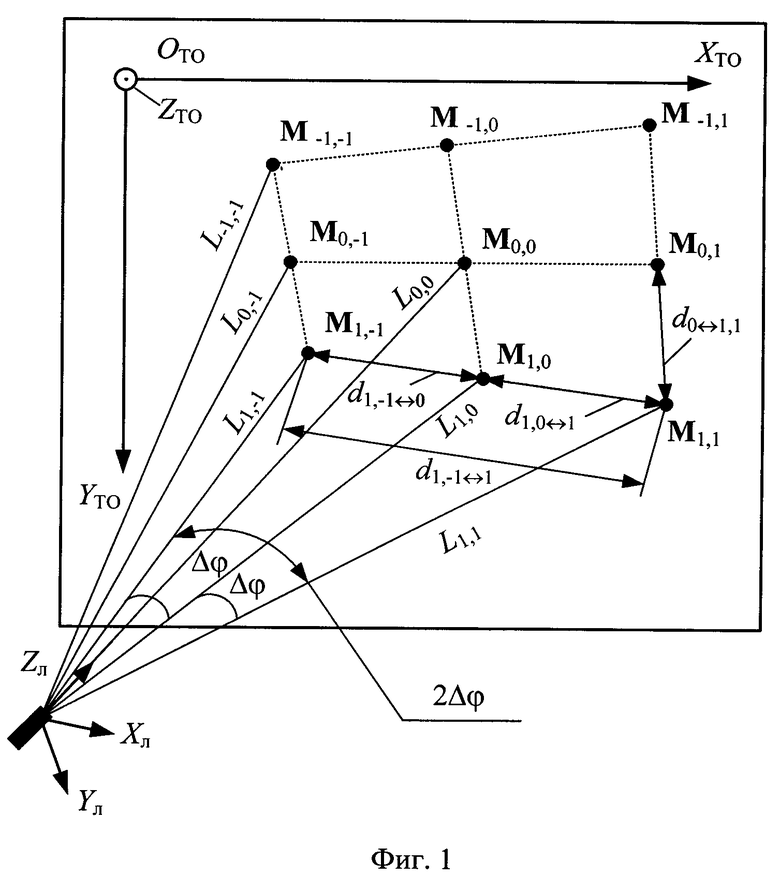
1. Способ взаимной калибровки видеокамеры и устройства веерного лазерного подсвета, в котором формируют массив снимков планарного тест-объекта с различных ракурсов и расстояний, для каждого ракурса наблюдения тест-объекта определяют координаты его характерных точек в системах координат камеры и лазерного устройства, выполняют репроекцию точек с известными в системе координат лазерного устройства координатами на изображение с камеры и итеративно с помощью численного алгоритма оптимизации уточняют матрицу поворота и вектор параллельного переноса между системами координат камеры и лазерного устройства, отличающийся тем, что угловое расстояние между лучами устройства веерного лазерного подсвета составляет единицы градусов, а также тем, что измеряют пространственные координаты проекций точек лазерного подсвета на плоскость тест-объекта в системе координат тест-объекта, вычисляют линейные расстояния между данными точками в каждой строке и в каждом столбце сетки проекций, по теореме косинусов составляют переопределенную относительно неизвестных расстояний от устройства лазерного подсвета до проекций точек подсвета систему нелинейных уравнений, решают ее численным методом и вычисляют пространственные координаты проекций точек подсвета на плоскость тест-объекта в системе координат устройства веерного лазерного подсвета.
2. Способ по п. 1, отличающийся тем, что для составления переопределенной системы уравнений по теореме косинусов выбирают треугольники с двумя вершинами в проекциях точек подсвета на плоскость тест-объекта по строке или столбцу и третьей вершиной в начале системы координат устройства лазерного подсвета.
| Способ получения цианистых соединений | 1924 |
|
SU2018A1 |
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| СПОСОБ АВТОКАЛИБРОВКИ СТЕРЕОКАМЕР, ИСПОЛЬЗУЕМЫХ В ЦЕЛЯХ АВТОМАТИЧЕСКОГО РАСПОЗНАВАНИЯ ЛИЦА ЧЕЛОВЕКА | 2015 |
|
RU2595620C1 |
| WO 2012143649, 26.10.2012. | |||
Авторы
Даты
2023-01-24—Публикация
2021-11-22—Подача