ПРИБОР ДЛЯ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И ДЛЯ НАХОЖДЕНИЯ КОРНЕЙ ЧИСЛЕННЫХ УРАВНЕНИЙ Советский патент 1926 года по МПК G06G3/08 

Во многих вопросах математической физики (задачи теории упругости, гидродинамики, электричества) вопрос сводится к нахождению функции u двух независимых переменных X и Y, удовлетворяющей уравнению в частных производных 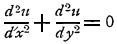в некоторой области изменений X и Y при заданных условиях на контуре этой области.

Предлагаемый прибор имеет целью механическое решение этой задачи при всех, обычно встречающихся, условиях на контуре и, кроме того, решение более общей задачи интегрирования уравнения а также нахождение корней (вещественных и комплексовых) каких угодно численных уравнений с любой степенью точности.

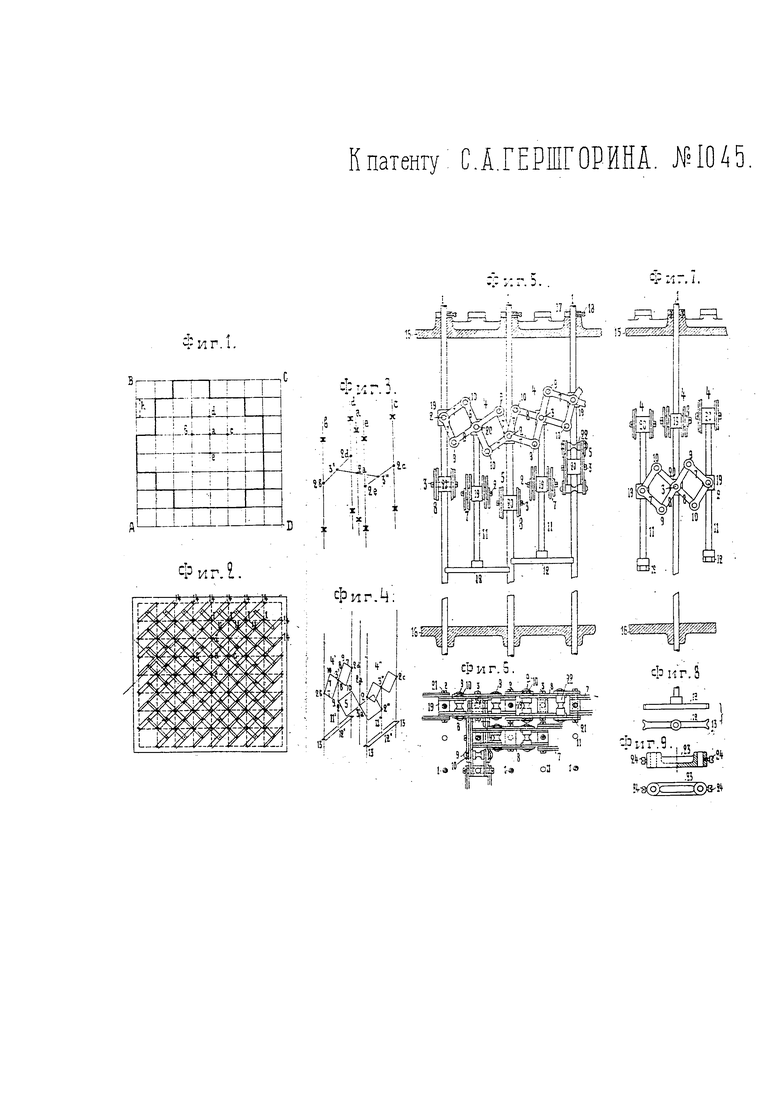
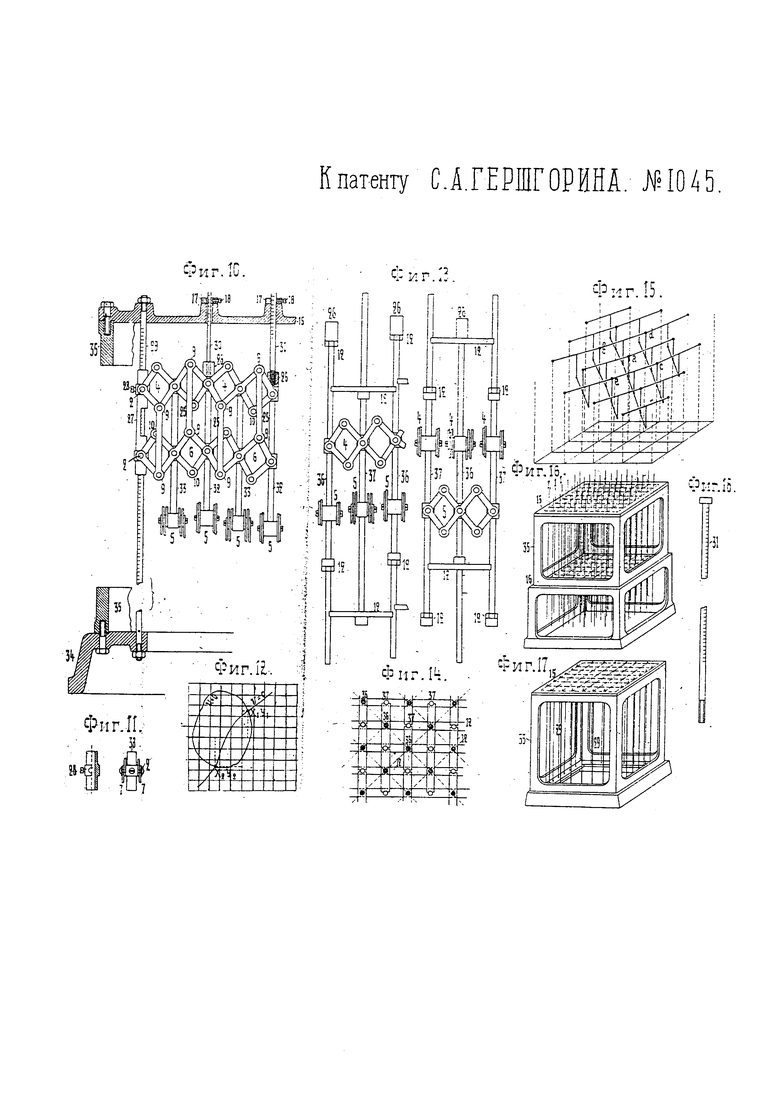
На фиг. 1, 3, 4 и 12 пояснена идея устройства и применения прибора; на фиг. 2 изображен схематический план прибора; на фиг. 5, 6, 7 - конструктивное осуществление элемента прибора в трех проекциях, при чем фиг. 5 представляет разрез по линии I-I фиг. 2, а фиг. 7 - разрез по линии II-II фиг. 2; фиг. 8 и 9 изображают детали устройства; фиг. 10, 13 и 14 - видоизменение в устройстве прибора; фиг. 11 и 18 - детали к ним; на фиг. 15 изображена общая схема соединений в приборе; на фиг. 16 и 17 - общий вид прибора.

Предлагаемый прибор основан на известном способе приближенного решения дифференциальных уравнений путем превращения их в уравнения в конечных разностях. Если принять, что переменные X и Y суть декартовы координаты на плоскости, то двумя взаимно - перпендикулярными системами равностоящих прямых, параллельных осям координат, делится плоскость на сеть квадратиков со стороной h (фиг. 1). В дальнейшем рассматривается значение искомой функции u только в вершинах этой сети. Перейдя, таким образом, к прерывному ряду значения функций, можно вторую производную заменить второй разностью, деленной на h². Следовательно, на основании известной формулы для вторых разностей, значения производных в какой-нибудь точке а (фиг. 1) выразятся так:

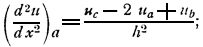
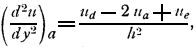
где u_n означает значение функций в точке n.

На подстановке этих значений уравнение принимает такой вид:

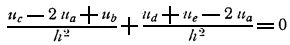
Умножив уравнение на h² и перенеся u_a в левую часть, получается:

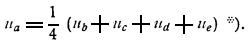
Это уравнение и должно рассматривать вместо уравнения Лапласа. Ему должны удовлетворять значения искомой функции во всех точках. Оно показывает, что в каждой точке значение u есть среднеарифметическое значение той же функции в 4 соседних точках. Если теперь задать значение функции u на контуре, то благодаря зависимости *), значение функции внутри контура определяется однозначно. Контуром может служить, как основной контур прибора (в данном случае, стороны квадрата ABCD), так и всякая другая кривая, расположенная внутри его. Его вид задается условиями задач. Если контур криволинейный, он должен быть заменен подходящей ломанной, вроде изображенной жирным шрифтом на фиг. 1.

Основная идея прибора состоит в следующем:

Во всех вершинах квадратной сетки, проведенной внутри квадрата ABCD, помещаются спицы, перпендикулярные к плоскости XY и могущие перемещаться в своем собственном направлении. Если между спицами создать такую механическую связь, чтобы высота поднятия какой-нибудь спицы 1а над некоторой основной плоскостью, параллельной плоскости XY, была равна средне-арифметическому между высотами поднятия 4 соседних спиц (1_b, 1_c, 1_d, 1_e), то при любом положении механизма высоты спицы будут давать в соответствующих точках значение некоторой функции u, удовлетворяющей уравнению *) и, следовательно, уравнению Лапласа. Для того, чтобы это решение подчинялось заданным условиям на контуре, нужно в каждой точке, лежащей на контуре, поднять спицу на величину, равную заданному значению функции u в данной точке контура и затем закрепить ее в указанном положении. По мере установки контурных спиц на требуемой высоте, спицы внутри контура будут передвигаться сами собою, и с закреплением последней спицы на контуре все внутренние спицы займут нужное положение. Остается измерить высоты всех спиц над основной плоскостью при помощи нанесенных на спицы делений или посредством масштаба: они и дадут решение данной задачи.

На фиг. 3 пояснено, как достигается требуемая связь между спицами. Пусть 2_a, 2_b, 2_c, 2_d и 2_е - постоянные точки на соответствующих спицах, одинаково удаленные от их концов. Соединим точки 2_b и 2_d таким образом, чтобы получить точку 3^I, которая всегда лежала посередине отрезка, соединяющего точки 2_b и 2_d. Высота этой точки над основной плоскостью будет всегда равна средне-арифметическому высот точек 2_b и 2_d. Соединяя точно так же точки 2_с и 2_е, получится точка 3′′, обладающая по отношению к последним аналогичным свойством. Если теперь соединить точку 2_а спицы 1_а с точками 3′ и 3′′ таким же образом, т.е. так, чтобы высота точки 2_a была средне-арифметической высот последних, то высота точки 2_а будет средне-арифметической высот точек 2_b, 2_c, 2_d, 2_e.

Требование, чтобы некоторая точка всегда находилась на середине отрезка, соединяющего две другие точки, осуществляется посредством параллелограммного механизма, представляющего собою двойной шарнирный четырехугольник или параллелограмм (фиг. 4). На фиг. 4, дающей схематическое осуществление построения фиг. 3, имеются 3 совершенно одинаковых двойных параллелограмма 4′, 4′′ и 5, каждый из которых состоит из четырех одинаковых коротких планок 7 и двух одинаковых длинных планок 8. Эти 6 планок соединены между собою в шарнирах 2, 3, 9 и 10. Оси шарниров 2 проходят через одноименные точки спиц. При описанном устройстве ось среднего шарнира 3 всегда будет находиться посредине между точками 2 соединяемых спиц при всех относительных положениях последних. Оси шарниров 3′ и 3′′ параллелограммов 4′ и 4′′ соединены с подвесками 11′ и 11′′, вертикальность которых обеспечивается поперечинами 12′ и 12′′ (фиг. 8), прикрепленными к ним перпендикулярно и оканчивающимися вилками 13, охватывающими соответствующие спицы, играющие в данном случае роль направляющих. Вертикальности подвесок 11 можно достигнуть и другими способами, например: 1) прибавив наряду с параллелограммом 4 еще второй комплект параллелограммов, присоединенных так, как параллелограммы, 6 на фиг. 10 (см. ниже), благодаря чему подвеска 11, две точки которой постоянно будут находиться на равных расстояниях от обоих параллельных между собою спиц, сама станет им параллельной, или 2) продолжив подвески книзу в виде спицы, пропустить их через направляющие отверстия нижней крышки, подобно основным спицам (слово вертикальность здесь и в дальнейшем понимается в условном смысле, так как ориентация прибора в пространстве не играет роли). Параллелограмм 5, плоскость которого перпендикулярна к плоскости параллелограммов 4′ и 4′′, соединяет точки 2′ и 2′′ подвесок с точкой 3_а спицы 1_a, при чем расстояния 2′3′=2′′3′′=2_a3_a, благодаря чему эффект достигается такой же, как при непосредственном соединении точек 3′, 3′′ и 2_а. Фиг. 4 дает лишь один элемент механизма, принадлежащий точке а. Им даются значения в точке а, как только даны значения в точках b, с, d и е. В свою очередь, точка с, напр., совершенно так же связана со своими соседними точками и т.д. Общий план прибора представлен схематически на фиг. 2, из которой видно, что все параллелограммы распадаются на две системы, параллельные обеим диагоналям квадрата, при чем на каждую спицу и подвеску (за исключением контурных спиц 14) приходятся параллелограммы обеих систем. На фиг. 15 показана общая схема механизма в перспективе, при чем параллелограммы условно обозначены отрезками, соединяющими соответствующие точки.

На фиг. 5, 6 и 7 дано конструктивное выполнение машины в трех проекциях. Спицы 1 проходят через отверстия в верхней крышке 15 и нижней 16. К верхней крышке прикреплены охватывающие спицы, кольца 17, в которые сбоку входят винтики 18, посредством которых каждая спица может быть зажата на любой высоте. На спицах и подвесках имеются утолщения в виде квадратов 19 и 20, которые служат для присоединения параллелограммов. Через них пропущены шарнирные болты 2 и 3, на выступающие концы которых насажены одноименные параллелограммные шарниры и которые как-нибудь предохранены от бокового выдвигания, напр., посредством шплинтов 21. Соединительные двойные параллелограммы в действительности сделаны парными, по одному с каждой стороны квадрата, и стянуты распорными стяжками 22, концы которых одновременно являются цапфами шарниров 9 и 10. Общий вид прибора показан на фиг. 16, при чем для ясности весь механизм опущен.

Во многих случаях на контуре задаются не значения функции, а значения ее частных производных по X и Y, т.е. при переходе к разностям, разности значений функции в двух соседних точках. Для осуществления такого условия устанавливается между соответствующими спицами требуемая разность высот, и затем они жестко соединяются в этом положении с помощью хомута 23 (фиг. 9), надеваемого на спицы и закрепляемого на них посредством винтов 24.

В описанном приборе рабочей частью спицы является часть 19-20; вся остальная часть служит лишь для направления движения этой части по определенной вертикальной прямой. В конструкциях фиг. 10 и 13 последнее достигается другим путем. Поэтому в приборе, изображенном на фиг. 10, спицы 1 заменены подвесками 32, которые соединены между собою и с вспомогательными подвесками 33, соответствующими подвескам 11 фиг. 5, по прежней схеме, только вместо каждого параллелограммного механизма 4 имеется пара совершенно одинаковых параллелограммных механизмов 4 и 6, расположенных один над другим и соединенных в шарнирах 9 планками 25. Так как по длине отрезки 22=33=99, то, благодаря указанному соединению, все подвески постоянно сохранят взаимную параллельность. В точках 14 (фиг. 2) расположенные на контуре квадрата ABCD подвески 32 заменены ползушками 27, скользящими по неподвижно закрепленным спицам 29, чем обеспечивается 1) их вертикальность и 2) отсутствие боковых перемещений. Первое обстоятельство влечет за собою вертикальность всех подвесок 32 и 33. Благодаря второму уничтожается возможность боковых смещений внутренних подвесок. Действительно, такие перемещения в направлении, напр., X, при условии вертикальности всех спиц, связаны соотношением *) на том же основании, что и вертикальные перемещения, и, следовательно, удовлетворяют уравнению Лапласа. Но известно, что решение уравнения Лапласа, равное нулю на всем контуре, тождественно равно 0 и внутри его. Из вышеприведенного видно было, что боковые перемещения на контуре равны 0. Следовательно, и для всех внутренних точек они неизбежно будут равны 0. Подвески 32 снабжены сверху головкой 26 с гаечной нарезкой. Показания в каждой точке могут быть прочтены, либо опуская сверху через отверстие в крышке специальный измерительный стержень до встречи с подвеской, либо при помощи легких спиц-указателей 30, ввернутых в гаечную нарезку. При необходимости установить какую-нибудь подвеску на желаемой высоте, в них ввинчивается спица 31 (фиг. 18), зажимаемая в кольце 17 винтом 18. Можно также, непосредственно, продолжив верхнюю часть подвески 32, пользоваться ею для закрепления и как указателем.

Другое видоизменение прибора, тоже без спиц, показано на фиг. 13. Прибор имеет подвески 35, выполняющие роль спиц, и вспомогательные подвески 37. Каждая подвеска имеет по две поперечины 12 (фиг. 8), которые скользят по тем двум соседним подвескам, с которыми она непосредственно соединена параллелограммным механизмом 4 или 5. Общая картина расположения поперечин показана на фиг. 14. Из нее видно, что каждая подвеска будет вполне надежно направляться но своей вертикальной прямой. Соединение параллелограммами выполнено так же, как; на фиг. 5. На контурных спицах скользят ползуны 38 (фиг. 11). В остальном прибор вполне сходен с прибором, изображенным на фиг. 10. Внешний вид обоих последних дан на фиг 17.

Интегрирование уравнения вида 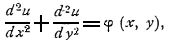где φ есть данная функция от X и Y (уравнение Пуассона), тоже сводится к решению уравнения Лапласа. С переходом к конечным разностям уравнение приобретает вид: 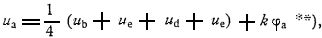где 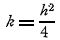- постоянная величина. Пусть значения функции u на контуре (они считаются заданными) будут u₀. Можно составить сколько угодно произвольных решений уравнения **), не задаваясь определенными. значениями на контуре. Напр., при произвольных значениях в двух первых горизонтальных рядах точек сетки получится из соотношения **) значения: в третьем ряду и т.д. Полученное таким образом решение обозначено через u₁, а его значение на контуре через u₁₀. Предполагается, что искомое u=u₁+u₂. Тогда все сводится к разысканию функции u₂, удовлетворяющей уравнению Лапласа: 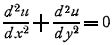при условиях на контуре u₂₀=u₀-u₁₀, что выполняется предлагаемым прибором.

Корни численных уравнений находятся на следующих основаниях: пусть дано уравнение ƒ(z)=0, где z рассматривается, как комплексная переменная x+iy. Функция ƒ(x+iy) распадается на две части - вещественную и мнимую - таким образом: ƒ(x+iy)=u(х, y)+iυ(х, у), при чем доказано, что полученные таким образом функции u и υ должны удовлетворять уравнению Лапласа и, следовательно, даются предлагаемым прибором по установке соответствующих значений на контуре. Поэтому вычисляются значения функции u в точках, лежащих на контуре квадрата ABCD и они устанавливаются на соответствующих спицах, после чего внутренние спицы дадут значения функции u внутри квадрата. На основании их, интерполируя, где нужно, между соседними спицами, строится на чертеже кривая u=0. Если поступить также с функцией υ, то получается кривая υ=0. Точки пересечения этих кривых x₁, у₁ и х₂, y₂ дадут комплексные корни х₁+iy₁ и х₂+iy₂ (фиг. 12). Вещественные корни получаются, как частные случаи комплексных. Значение каждого корня может быть уточнено, если маленький квадрат, в котором он лежит, рассмотреть, так сказать, "микроскопически", т.е. распространить его на весь квадрат ABCD и повторить указанный процесс, что, очевидно, можно продолжить до бесконечности.

1. Прибор для интегрирования дифференциальных уравнений Лапласа и Пуассона и для нахождения корней численных уравнений, отличающийся применением: а) расположенных в шахматном порядке параллельных друг другу спиц 1 (фиг. 4 и 7), свободно скользящих в отверстиях в крышке 15 и 16 прибора и в связи с контурными условиями, либо зажимаемых на определенной высоте, либо спариваемых посредством хомутика 23 (фиг. 9); б) подвесок 11, устанавливаемых параллельно основным спицам 1, и в) шарнирных параллелограммов 4, 5, расположенных параллельно обоим диагоналям квадратов и соединяющих спицы 1 между собою и с подвесками 11 таким образом (фиг. 4 и 15), чтобы перемещение каждой спицы было равно среднему арифметическому перемещению четырех ближайших соседних спиц.

2. Видоизменение указанного в п. 1 прибора, отличающееся применением, вместо спиц 1, подвесок 32 (фиг. 10), соединенных между собою и с вспомогательными подвесками 33 при помощи шарнирных параллелограммных механизмов 4 и 6, расположенных друг над другом и сочлененных в вершинах 9 планками 25, с целью не только получения требуемого соотношения между перемещениями, но и направления движения подвесок по определенной прямой.

3. Видоизменение указанного в п. 1 прибора, отличающееся применением, вместо спиц 1, подвесок 36 (фиг. 13) и вспомогательных подвесок 37, несущих каждая две поперечины 12, снабженные на концах вилками 13, захватывающими за соседние подвески, с целью направления их движения.