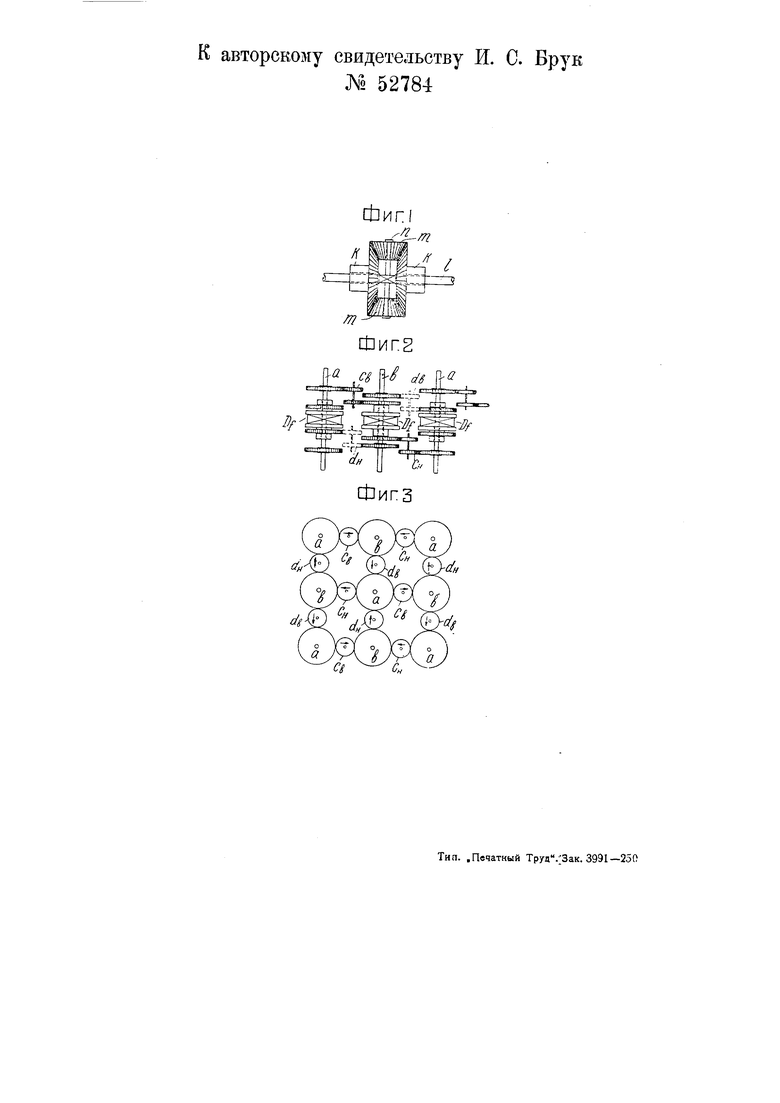
Заявлено 11 мая 19 Опубликовано 31 Предлагаемый прибор предназначен для интегрирования уравнения Лапласа, имеющего, как известно, вид дЧ1 , d4J f. dxf Т с1у2 - где X и у - координаты точек плоскости, а и-значение функции в этих точках. Согласно изобретению, в приборе применены валы, снабженные диференциалами, причем валы соединены с соседними диференциалами при помощи зубчатых передач таким образом, чтобы угол поворота любого вала был равен среднему арифметическому из углов поворота четырех окружающих валов, расположенных по вершинам квадрата. На фиг. 1 чертежа изображен обычный диференциал, на фиг. 2 и 3- схема расположения валов в предлагаемом приборе в двух проекциях. Каждый вал снабжен диференциалом, составленным из конических шестерен (фиг. 1). Шестерни /С сидят свободно на сквозной оси /. Ось п, несущая малые шестерни т, жестко связана с осью /. Если углы поворота шестерен К около оси / равны fi и %, .: года за арта 193 1-Ода/,-. 1 , , L ,... угол поворота оси / будет равен -Y Прибор по фиг. 2 и 3 состоит из ряда валов а, Ь, установленных параллельно. Каждый вал снабжен диференциалом D/ по фиг. 1, в котором на конических шестернях К предусмотрены цилиндрические зубчатки, служащие для связи с соседними валами через передачи Св, С„, rf,, du. По расположению шестерен и передач валы разделяются на два вида а и Ь. Валы а являются основными, валы b промежуточными. Передачи между валами выполнены четырех родов: от вала. а.к верхней шестерне диферени,иапаЬ (такие передачи обозначены через с, ), от вала а к нижней ше1ЬЛ-ИЛ-т f хстерне диференциала о (обозначены через С„ ), от вала b к верхней шестерне диференциала вала а и наконец от вала b к нижней шестерне диференциала вала а (обозначены соответственно rf, и rf ). Проследив действие устройства, можно убедиться, что угол поворота промежуточного вала 6, расположенного между двумя валами а, которым заданы повороты и -fo, будет равен у- Лналогично, вал Ь,
расположенный между валами а с углами поворота fg и , повернется
на угол . Следовательно, угол
поворота вала, расположенного на фиг. 3 посередине,
со - 1 + 2 + У8 + 4
Vs -4
т. 6. равен среднему арифметическому углов поворота четырех основных окружающих его валов.
Чтобы пояснить применение этого устройства для решения уравнения Лапласа, следует преобразовать последнее, заменив бесконечно малые конечными разностями. Тогда вместо вторых частных производных следует ввести вторые разности функции X VI у, положив приращения координат одинаковыми, например, Ал; Ду 1. Пусть в некоторой точке плоскости с координатами x tn и у п значение функции 6 будет (Jm,,,, а в точке с координатами m-f-l, п она равна f/,n+i, п. Тогда выражение для второй разности функции LJ, взятой по направлению оси X, можно представить в следующем виде
Д ( U-in + l, п 2 Urn, п -f- , н
Аналогично вторая разность по направлению оси у
А и и, „+1 - 2 и,п, п 4- О., „-1.
Подстановка этих выражений в уравнение Лапласа, переписанное в конечных разностях
Д. fy + Д, 0, сразу дает
i/in+l, -(-f/m, и-i-{-Um-l, n-}-Um, n-J-1
7- Um,n,
Это выражение показывает, что значение функции и в точке (т, п) должно равняться среднему арифметическому из значений функции в
вершинах квадрата, в центре которого находится точка (т, п).
В описанном выше приборе поворот четырех основных валов, расположенных по вершинам квадрата, вызывает поворот центрального вала, удовлетворяющий этому условию. Следовательно, увеличив до нужного количества число валов в приборе, можно применить его для приближенного решения уравнений Лапласа. Для этого нужно повернуть валы, расположенные на ограничивающем контуре, соответственно значениям функции и на этом контуре. Все остальные валы а, расположенные внутри контура, повернутся на углы, соответствующие значениям fJ в точках, где расположены эти валы. Снабдив валы приспособлениями для отсчета углов, можно с требуемой точностью определить эти углы и, следовательно, найти приближенные значения во всех соответствующих валам точках плоскости ху, причем значения U на контуре могут быть как положительными, так и отрицательными.
Предмет изобретения.
1.Прибор для интегрирования уравнений Лапласа, отличающийся применением ряда расположенных нормально плоскости, в которой расположена область интегрируемой функции, валов а и Ь, снабженных каждый диференциалом D/ и соединенных между собой зубчатыми передачами, образующими систему валов, причем угол поворота любого вала системы равен среднему арифметическому из углов поворота смежных с ним валов.
2.Применение в приборе по п. 1 промежуточных зубчатых передач с и d, с целью придания основным валам, для удобства отсчета углов поворота, одностороннего вращения.
к авторскому свидетельству И. С. Брук
№ 52784

| название | год | авторы | номер документа |
|---|---|---|---|
| Прибор для интегрирования уравнений Лапласа | 1936 |
|
SU52785A1 |
| Множительный прибор | 1947 |
|
SU74675A1 |
| Прибор для контроля и разметки гребных и т.п. винтов | 1945 |
|
SU68379A1 |
| Потенциометрическое устройство для решения алгебраических уравнений | 1948 |
|
SU83582A1 |
| Электрический прибор для определения и визуального отсчета на экране катодно-лучевой трубки корней алгебраического уравнения n-й степени | 1948 |
|
SU78876A1 |
| Прибор для автоматической съемки плана железнодорожного пути | 1928 |
|
SU19803A1 |
| Устройство для приближенного интегрирования графически заданных функций | 1937 |
|
SU53632A1 |
| Однопроводная силовая синхронная передача | 1948 |
|
SU83673A1 |
| Потенциометрическое устройство для решения системы линейных алгебраических уравнений | 1949 |
|
SU83457A2 |
| ПОВОРОТНЫЙ СТОЛ ДЛЯ ИСПЫТАНИЯ ПРИБОРОВ | 1935 |
|
SU47096A1 |

О- ds Pf
сЬиг
т
/{
Шиг2
ФигЗ
Авторы
Даты
1938-01-01—Публикация
1936-05-11—Подача