Область техники
Данное заявленное изобретение относиться к области ремонта оборудования АЭС, конкретно касается метода идентификации дефектов в отверстиях под шпильки главного разъема (далее отверстия) корпуса реактора.
Уровень техники
Корпус ядерного реактора является одним из важнейших узлов АЭС, и его качество имеет ключевое значение для обеспечения нормальной и безопасной эксплуатации ядерных энергетических систем. При обратной установке шпилек главного разъема в отверстия необходимо обеспечить высокую чистоту поверхности резьбы без заусенцев и посторонних предметов. Поэтому перед установкой необходимо проверить поверхность резьбы отверстий на соответствие соответствующим требованиям.
В настоящее время обычно используются устройства видеоконтроля для получения изображения отверстий, а затем визуально определяют чистоту резьбы и отсутствие дефектов, а также форму и размер дефектов, глядя на видео или изображение поверхности резьбы. Кроме того, оператор должен быть высококвалифицированным и иметь большой опыт работы на площадке, чтобы иметь возможность делать относительно точную оценку. Длительное наблюдение оператора за резьбой может легко вызвать зрительное утомление, что может привести к ошибочной или пропущенной оценке.
Раскрытие изобретения
Целью настоящего изобретения является создание метода трехмерной реконструкции резьбы отверстий под шпильки главного разъема корпуса реактора и автоматической идентификации дефектов, который позволяет быстро и точно контролировать резьбу в трехмерном масштабе, идентифицировать дефекты и вычислять размеры дефектов, а также выводить результаты контроля.
Техническое решение данного изобретения описано ниже:
Способ трехмерной реконструкции резьбы отверстий под шпильки главного разъема корпуса реактора и автоматической идентификации дефектов включает следующие шаги:
шаг 1: провести сканирование для получения двумерных координат поверхности резьбы;
шаг 2: информация о 2D-координатах поверхности резьбы, угловые данные сканирующего устройства и данные осевого положения объединяются в данные 3D-координат, т.е. 3D-данные облака точек;
шаг 3: провести предварительную обработку 3D-данных облака точек, определение вектора нормали 3D-данных облака точек и разделение 3D-данных облака точек на гладкую область и резкую область, а также их фильтрацию и обесшумливание отдельно;
шаг 3: сжатие 3D-данные облака точек с сохранением данных, превышающих пороговое значение;
шаг 5: провести трехмерную реконструкцию кривой поверхности контролируемого объекта и создать сетчатую модель;
шаг 6: провести идентификацию и измерение дефектов, характеризовать дефекты параметрами и выводить тип дефектов.
Указанный шаг 1 заключается в следующем:
сначала создать две системы координат: одна система координат oxz с собственной опорной точкой сканирующего устройства в качестве исходной точки, а измеренные 2D-данные поверхности резьбы представляют собой координаты точки в системе координат oxz, которые характеризуются как (x,z). Другая - система координат O2XYZ отверстия, O2 обозначает центр окружности в нижней плоскости отверстия, Z - направление оси отверстия вверх, X - тангенциальное направление по часовой стрелке к центру отверстия главного разъема корпуса реактора, Y - направление, указывающее на центр корпуса реактора, направление этой оси координат определяется в соответствии с правилом правой руки, H - высоту сканирующего устройства относительно дна отверстия, а θ - угол проекции сканирующего устройства на плоскость OXY в текущей системе координат;
после маркирования отверстий, подлежащих проверке, позиционирования и установки сканирующего устройства, сканирующая головка опускается до начального участка резьбы, поворачивается на один круг и синхронно собирает двумерные данные. Сканирующая головка поднимается до верха, и сканирующее устройство перемещается для продолжения сканирования всех отверстий для получения 2D-координат всех отверстий.
Указанное сканирующее устройство представляет собой структурированный световой сканер, который устанавливается на корпусе машины для позиционирования. Путем перемещения корпуса машины на поверхности фланца корпуса реактора вдоль положения различных отверстий осуществляет сканирование каждого отверстия, при достижении до положения одного отверстия из них с определенным номером сначала провести позиционирование корпуса машины для обеспечения фиксации положения корпуса машины относительно корпуса реактора при сканировании,
перед тем как сканирующая головка поднимется до верха, необходимо определить, достигает ли сканирующая головка до дна отверстия. Если она не достигает верха, то сканирующая головка опускается, а затем снова вращается на один круг, и 2D-данные собираются одновременно, пока она не достигнет дна.
Указанный шаг 2 заключается в следующем:
2D-данные поверхности резьбы, координаты которых характеризуются как (x,z) в системе координат oxz, а расстояние между опорной точкой сканирующего устройства и центром отверстия является постоянным, и обозначается как D, можно получить 3D-данные облака точек, то есть координаты (x,z) в системе координат O2XYZ, обозначаемые как:
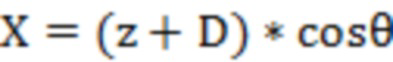
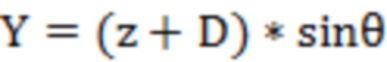
 .
.
Указанный шаг 3 заключается в следующем:
шаг 3.1: построить k-окрестность для полученных данных облака точек и вычислить вектор нормали облака точек. Провести оценку вектора нормали облака точек с помощью метода PCA и получить множество k точек пробоотбора, ближайших к точке пробоотбора pi в данных облака точек;
шаг 3.2: вычислить нормальное расстояние от точки пробоотбора до локальной касательной плоскости в ее k-окрестности. Классифицировать точки пробоотбора по характеристикам в соответствии с пороговым значением расстояния и разделить 3D-данные облака точек на гладкую и резкую области. Нормальное расстояние от точки пробоотбора до локальной касательной плоскости в окрестности определяется как гладкая область, если оно меньше или равно пороговому значению, и резкая область, если оно больше порогового значения.
Шаг 3.3: провести фильтрацию и обесшумливание гладкой и резкой областей соответственно.
Алгоритм двусторонней фильтрации используется для фильтрации и обесшумливания резкой области.
В частности, используется следующая формула:
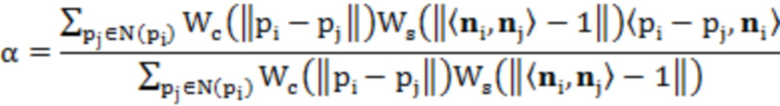
где pi - текущая обрабатываемая точка в наборе облаков точек; pj - точки в окрестности pi; ni, nj - векторы нормали pi, pj соответственно; α - коэффициент двусторонней фильтрации; Wc - гауссова керн-функция в пространственной области; Ws - гауссова керн-функция в частотной области.
Данные облака точек после фильтрации выражаются следующим образом:

здесь n - вектор нормали к касательной плоскости точки пробоотбора, 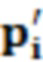 - положение облака точек после фильтрации.
- положение облака точек после фильтрации.
Провести фильтрацию и обесшумливание с использованием алгоритма взвешенного локального оптимального проецирования для гладкой области.
Конкретно в следующем:
использовать локальную информацию для локального улучшения данных облака точек. Путем введения весовой функции плотности создать наборы точек с более равномерным распределением, улучшить равномерность распределения облаков точек и гладкость поверхности, при этом используется следующая итерационная формула:
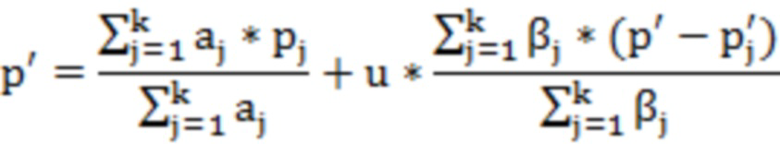
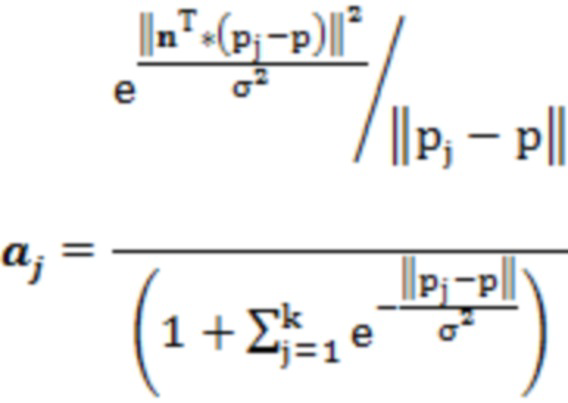
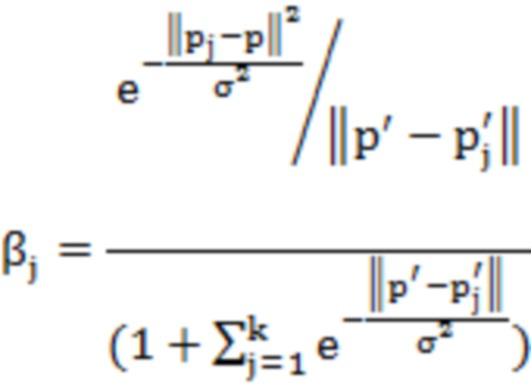
где u - константа, p - самое исходное положение облака точек, 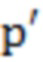 - новое положение после итерации,
- новое положение после итерации,  - количество смежных вершин,
- количество смежных вершин, 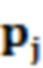 - текущая точка пробоотбора исходного облака точек,
- текущая точка пробоотбора исходного облака точек,  - выходное значение точки пробоотбора после итерационной операции,
- выходное значение точки пробоотбора после итерационной операции, 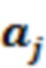 и
и 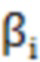 - соответствующие весовые коэффициенты, σ - стандартное отклонение текущей точки облака точек в окрестности, e- естественная константа.
- соответствующие весовые коэффициенты, σ - стандартное отклонение текущей точки облака точек в окрестности, e- естественная константа.
Указанный шаг 4 заключается в следующем:
во-первых, с помощью метода сферического линейного уравнения, основанного на методе наименьших квадратов, провести оценку кривизны 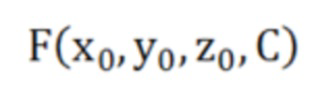 данных облака точек после фильтрации и обесшумливания (шаг 3) по следующей формуле:
данных облака точек после фильтрации и обесшумливания (шаг 3) по следующей формуле:
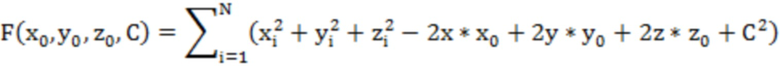
где 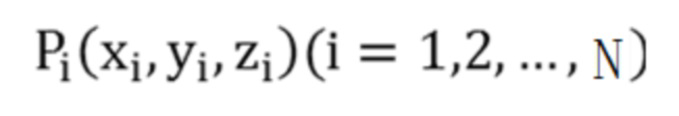 - координаты точек xi, yi, zi на сферической поверхности в системе координат O2XYZ;
- координаты точек xi, yi, zi на сферической поверхности в системе координат O2XYZ;  - координаты центра сферы; R - радиус сферы; С - константа, подлежащая решению; N – количество точек подогнанной сферической поверхности, а координаты соседних точек из набора облака соседних точек с центром
- координаты центра сферы; R - радиус сферы; С - константа, подлежащая решению; N – количество точек подогнанной сферической поверхности, а координаты соседних точек из набора облака соседних точек с центром 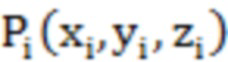 подставляются в вышеприведенную формулу для получения серии систем уравнений, С получается методом наименьших квадратов;
подставляются в вышеприведенную формулу для получения серии систем уравнений, С получается методом наименьших квадратов;
затем создать локальную систему координат, параллельно перенести исходную точку для получения ее пространственных координат в новой локальной системе координат, и окончательно вычислить неизвестные параметры и кривизну.
Наконец, значение кривизны сравнивается с установленным пороговым значением. Если оно больше порогового значения, оно сохраняется, а если оно меньше порогового значения, оно отбрасывается.
Указанный шаг 5 заключается в следующем:
шаг 5.1 - провести оценку нормального вектора со взвешенной коррекцией
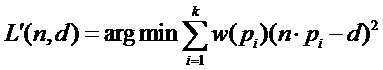
где n - вектор нормали касательной плоскости точки пробоотбора; d - расстояние от точки до подогнанной плоскости; k - количество точек окрестности;  - текущая точка пробоотбора;
- текущая точка пробоотбора; 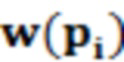 - взвешенное значение, выражение в следующем:
- взвешенное значение, выражение в следующем:
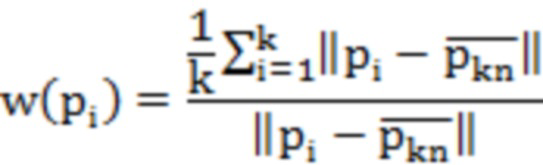
здесь  - центр тяжести k-окрестности
- центр тяжести k-окрестности  ;
;
шаг 5.2 -разделение облака точек и возвращение к множеству блоков.
Для ожидаемого разделения набора данных облака точек P на К областей сначала произвольно выбрать К точек из данных облака в качестве начальных центров К разделенных областей, вычислить евклидовое расстояние от каждой точки из облака точек до К начальных центров разделенных областей, распределить их в разделенные области, представленные ближайшими начальными центрами разделения, а затем настроить центр каждой разделенной области, повторять вышеуказанный процесс вычисления до тех пор, пока не изменятся все центры области, затем остановить итерацию, процесс разделения заканчивается, и выводится результаты разделения областей;
шаг 5.3 - провести поблочное прореживание и повторный отбор проб.
Вычислить кривизну точек в каждой области отдельно по разделенным областям блока, вычислить кривизну точки в каждой области отдельно и среднее значение кривизны в области. Если кривизна точки пробоотбора меньше среднего значения, то данная точка отбрасывается, в противном случае сохраняется отбор проб исходной точки;
шаг 5.4 -вычислить узловую функцию для достижения оптимизации сглаживания.
Фундаментальная функция узловой функции F0выражается как:
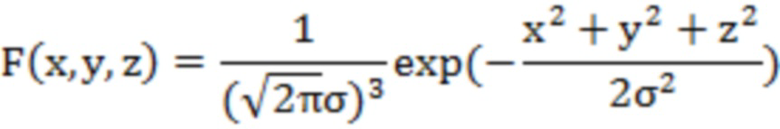
здесь  - стандартное отклонение гауссовской фильтрации;
- стандартное отклонение гауссовской фильтрации;
шаг 5.5 - вычислить глубину наибольшего октодерева дерева блоков.
Если задать максимальную глубину глобального октодерева равной Dmax, а минимальную глубину - Dmin, то максимальная глубина локального октодерева каждого блока облака точек может быть выражается как:
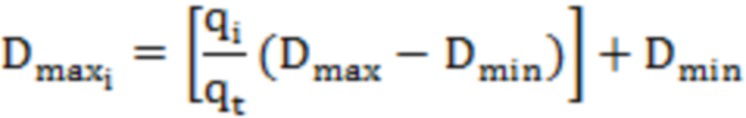
здесь среднее значение кривизны выражается как  ;
; 
шаг 5.6 - извлечение изоповерхности для получения отображения изоповерхности треугольниками в любом вокселе.
Определить, лежит ли его вершина вне или внутри изоповерхности, а затем определить схему разбиения изоповерхности по состоянию вершины.
Если значение данных вершины вокселя больше или равно значению изоповерхности, то вершина определяется как находящаяся вне изоповерхности и отмечается как положительная точка, т.е. 1. Если значение данных вершины вокселя меньше значения изоповерхности, то вершина определяется как находящаяся внутри изоповерхности и отмечается как отрицательная точка, т.е. 0.
Каждый воксель имеет в общей сложности восемь вершин, и каждая вершина имеет два состояния, положительное и отрицательное, а изоповерхности могут пересекать воксель в общей сложности 256 способами, образуя отображение изоповерхности треугольниками в любом вокселе.
Шаг 5.7 - создание сетчатой модели.
По положительному и отрицательному состоянию поля направленного расстояния 8 вершин получаются треугольники, координаты вершин треугольников, то есть точки пересечения края точек вокселя с реконструируемой кривой поверхностью получаются путем линейной интерполяции двух вершин края точек вокселя.
Указанный шаг 6 конкретно выполняется следующем образом:
шаг 6.1 - создание целевой функции идентификации дефектов

где  - облако точек в стандартной модели;
- облако точек в стандартной модели; 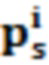 - облако точек, подлежащее подгонке; R - матрица поворота; T - матрица переноса; NP- количество облаков точек в стандартной модели; оптимальные R и T, которые вычислены методом наименьших квадратов; затем выполняется итерация до тех пор, пока вычисленное значение
- облако точек, подлежащее подгонке; R - матрица поворота; T - матрица переноса; NP- количество облаков точек в стандартной модели; оптимальные R и T, которые вычислены методом наименьших квадратов; затем выполняется итерация до тех пор, пока вычисленное значение 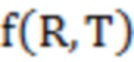 не будет минимальным;
не будет минимальным;
шаг 6.2 - кластерное разделение областей дефектов и извлечение характеристик.
Определить местоположение дефектов поверхности по расстоянию.
Среднее значение расстояний отклонения выражается как:
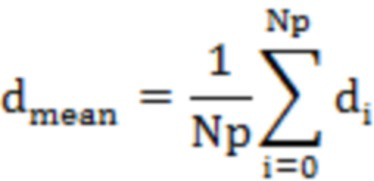
здесь di обозначает расстояние от точки до кривой поверхности модели облака точек;
определить расстояние отклонения всех точек и среднее значение, сохранить точку xi, соответствующую di, в классе X, когда di>dmean, и пройти все точки, чтобы выделить области с большим расстоянием отклонения от поверхности модели облака точек;
шаг 6.3 - характеризовать дефекты параметрами, определить площадь, периметр и соотношение длины к ширине дефекта и в конечном итоге выводить тип дефектов.
Площадь дефекта - это геометрическая характеристика, которая измеряет размер области дефекта. Метод расчета в следующем:
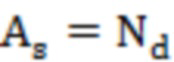
здесь 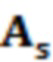 - площадь дефектной зоны; S – измеренная дефектная область;
- площадь дефектной зоны; S – измеренная дефектная область;  - количество облаков точек в дефектной области.
- количество облаков точек в дефектной области.
Периметр дефекта - это длина граничной контурной линии, которая окружает дефектную область и рассчитывается как:
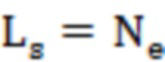
здесь 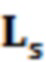 - периметр дефектной область;
- периметр дефектной область; 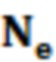 - количество характеристик границы дефектной области.
- количество характеристик границы дефектной области.
Соотношение длины к ширине дефекта используется для определения его формы и рассчитывается следующим образом:
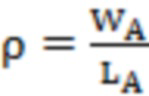 .
.
Значительный результат данного изобретения заключается в получении двумерных координат поверхности резьбы структурированным световым сканером, на основе информации о высоте и угле резьбы, полученной кодером, и вычислении трехмерных координат с помощью калибровочных параметров системы, фильтрации 3D-данных облака точек, реконструкции кривой поверхности резьбы и автоматической идентификации дефектов.
Сканирование с помощью структурированного светового датчика позволяет провести трехмерную реконструкцию поверхности резьбы, по сравнению с существующим методом формирования двумерного изображения резьбы, позволяет более четко представить трехмерные детали поверхности резьбы, дает более подробные данные для оценки и идентификации дефектов резьбы.
Расположение и перемещение структурированного светового датчика позволяет получать 3D-данные облака точек на поверхности резьбы с разрешением до 0,1 мм с помощью технологии синхронизации движения и преобразования координат. Условия испытания: испытать резьбовое кольцо стандартного размера методом данного оборудования для получения трехмерной модели этого резьбового кольца, основными характерными значениями которого являются большой диаметр, средний диаметр, малый диаметр, шаг резьбы, высота профиля резьбы, угол подъема резьбы и т.д. с погрешностью не более 0,1 мм от измеренного значения.
Процесс обработки данных облака точек, с помощью обесшумливания облака точек, сжатия данных и других операций, не только сохраняет подробную информацию о данных резьбы, но и упрощает модель, размер модели одного отверстия не превышает 100 M, что способствует сохранению и передаче файлов и последующей обработке для трехмерной реконструкции.
В настоящее время идентификация дефектов резьбы в основном зависит от искусственного тщательного наблюдения видеофайла, что легко вызывает визуальную усталость и приводит к ошибочной оценке, и имеет сильную субъективность. Данный метод трехмерной реконструкции поверхности резьбы и автоматической идентификации дефектов имеет более эффективный характер.
По данному методу можно полностью автоматически выполнить сбор, анализ и обработку данных всех отверстий, при этом время такой операции на одном отверстии не более 5 мин.
Краткое описание приложенных схем
Фиг. 1 - схема построения системы координат.
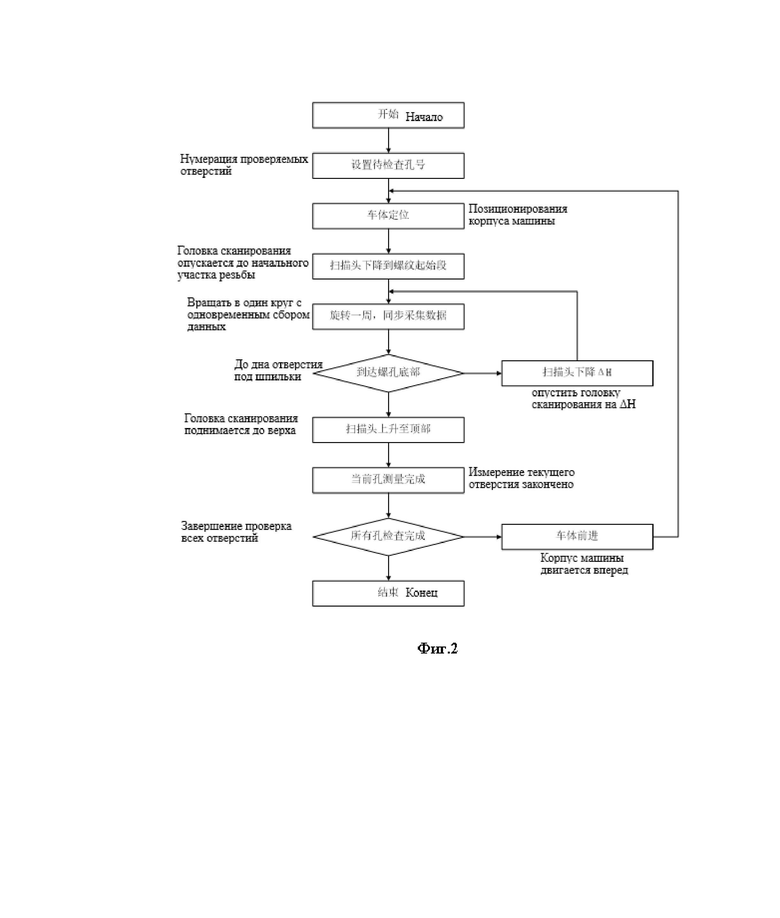
Фиг. 2 -схема сбора данных оборудования.
Фиг. 3 -схема сбора, построения и идентификации данных.
Фиг. 4 - схема предварительной обработки данных облака точек.
Фиг. 5 -схема реконструкции 3D-кривой поверхности.
Конкретный способ реализации
Ниже приведено дополнительное описание настоящего изобретения с помощью прилагаемых схем и конкретного способа реализации.
Шаг 1: сбор данных и преобразование координат.
Посредством вращательного движения и осевого движения структурированного светового сканера в реальном масштабе времени записать информации о 2D координатах сканера, одновременно записать угловые данные и данные осевого положения структурированного светового сканера, диапазон сканирования покрывает внутреннюю поверхность целого отверстия. Сканирование может проводиться по частям из-за ограничения диапазона сканирования структурированным светом.
Как показано на фиг. 1, отверстия представлены цилиндрической формой, а маленькие внутренние квадраты представляют структурированный световой сканер. Боковая темная треугольная область представляет структурированный свет, производимый структурированным световым сканером.
Создать две системы координат: одна система координат oxz с собственной опорной точкой (можно выбрать геометрический центр или выбрать точку света) структурированного светового сканера в качестве исходной точки, а 2D-данные, измеренные структурированным световым сканером представляют собой координаты точки в системе координат oxz, которые характеризуются как (x,z).
Другая - система координат O2XYZ отверстия, O1 обозначает центр окружности в верхней плоскости отверстия, O2 обозначает центр окружности в нижней плоскости отверстия, Z - направление оси отверстия вверх, X - тангенциальное направление по часовой стрелке центра отверстия корпуса реактора, Y - направление центра корпуса реактора, направление этой оси координат определяется в соответствии с правилом правой руки, H - высоту структурированного светового сканера относительно дна отверстия, а θ - угол проекции структурированного светового сканера в плоскости OXY при текущей системе координат.
Свет от структурированного светового сканера попадает на поверхность резьбы, и направление света параллельно оси отверстия. Установив механизм движения на структурированный световой сканер, он может совершать линейное движение вдоль оси отверстия в отверстии под шпильки главного разъема. Обычно диапазон измерения высокоточного датчика составляет 20 мм, а глубина отверстия больше 200 мм, можно осуществить полное ходовое покрытие отверстия движением датчика. В то же время механизм движения также позволяет структурированному световому сканеру выполнять вращательное движение вдоль оси отверстия.
Структурированный световой сканер получает двумерные данные, исходной точкой координат является точка, где свет выходит из этого датчика, ось x, по которой выходит свет, параллельна оси отверстия, а ось z перпендикулярна внутренней поверхности отверстия.
Высота от структурированного светового сканера до дна отверстия измеряется кодером, который предназначается для измерения высоты.
Угол θ между световой плоскостью сканера и осью X измеряется кодером для измерения угла. Процесс сканирования в нижеследующем: сканер сканирует верхнюю часть отверстия на один круг с одновременным записыванием координат всех точек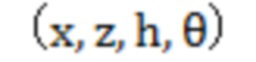 с помощью технологии синхронизации, после завершения сканирования снижается на ΔH, заново сканирует в один круг и собирает данные координат
с помощью технологии синхронизации, после завершения сканирования снижается на ΔH, заново сканирует в один круг и собирает данные координат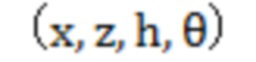 в реальном времени. Повторяя операцию несколько раз, пока сканер не достигнет дна отверстия для шпильки. Высота однократного снижения ΔH должна быть выбрана таким образом, чтобы процесс сканирования охватывал все области резьбы, и чтобы она не превышала диапазон измерения сканера в направлении оси z. После сканирования всего отверстия координаты каждой точки
в реальном времени. Повторяя операцию несколько раз, пока сканер не достигнет дна отверстия для шпильки. Высота однократного снижения ΔH должна быть выбрана таким образом, чтобы процесс сканирования охватывал все области резьбы, и чтобы она не превышала диапазон измерения сканера в направлении оси z. После сканирования всего отверстия координаты каждой точки 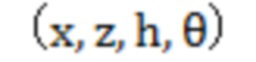 проектируются на
проектируются на 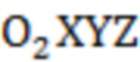 для получения трехмерного облака точек резьбы в отверстии.
для получения трехмерного облака точек резьбы в отверстии.
Подробный процесс сбора данных показан на фиг. 2.
1.1)Простановка номеров проверяемых отверстий.
В зависимости от типа реактора, корпус реактора обычно имеет от 48 до 58 отверстий под шпильки главного разъема, выполнить нумерацию всех отверстий под шпильки на корпусе реактора, подлежащих проверке.
1.2)Позиционирования корпуса машины.
Установить структурированный световой сканер на корпус машины, который передвигается вдоль положения разных отверстий на фланцевой поверхности корпуса реактора, чтобы осуществить сканирование каждого отверстия. При достижении положения одного из отверстий сначала выполнить позиционирование корпуса машины с обеспечением фиксации положения корпуса машины при сканировании относительно корпуса реактора.
1.3) Головка сканирования опускается до начального участка резьбы.
Головка сканирования - это имеет в виду головку сканирования структурированного светового сканера.
1.4) Вращать в один круг с одновременным сбором данных.
После того как головка сканирования структурированного светового сканера вращается в один круг с помощью механизма движения, производит измерение и получает 2D координатную информацию сканера.
1.5) Определить, достигает ли головка сканирования дна отверстия.
Если да, то перейти к шагу 1.6);
Если нет, то опустить головку сканирования на ΔH, после чего возвращать к шагу 1.4).
ΔH обычно составляет 2-10 мм;
Структурированный световой сканер имеет диапазон измерения 40 мм в направлении глубины отверстия, которая составляет около 260 мм, и поэтому его необходимо сканировать по участкам, спускаясь после каждого сканирования и затем сканируя, при этом сканер достигает дна отверстия, основываясь на действительном сигнале от нижнего концевого выключателя (фотоэлектрического типа) в осевом направлении.
1.6) Головка сканирования поднимается до верха.
Структурированный световой сканер имеет диапазон измерения 40 мм в направлении глубины отверстия, которая составляет около 260 мм, и поэтому его необходимо сканировать по участкам. После завершения сканирования текущего отверстия сканер поднимается до верха отверстия, основываясь на действительном сигнале от верхнего концевого выключателя (фотоэлектрического типа) в осевом направлении.
1.7) Корпус машины продолжает двигаться вперед и повторять вышеуказанные шаги 1.2) - 1.6), пока все отверстия не будут отсканированы и не будет получена информация о 2D координатах сканера после сканирования всех отверстий.
Шаг 2: Создание данных 3D облака точек.
В соответствии с геометрическим соотношением информация о двумерных координатах, данные об углах и данные об осевом положении резьбовой поверхности, полученные сканером, синтезируют трехмерные координатные данные, то есть данные трехмерного облака точек.
Структурированный световой сканер может получать двумерные данные, основанные на собственной опорной точке в качестве исходной точки, координаты которой характеризуются в системе координат oxz как (x,z). Текущий угол структурированного светового сканера θ измеряется фотоэлектрическим кодером, текущая высота H измеряется кодером в направлении глубины отверстия. Расстояние опорной точки сканера от центра отверстия является постоянным, обозначается как D, можно получить координаты в системе координат O2XYZ:
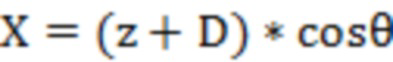
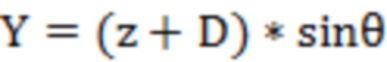
 .
.
Координаты (x,z) в системе координат oxz - это двумерные данные, полученные структурированным световым сканером.
Диапазон измерения структурированного светового сканера в направлении глубины отверстия составляет 40mm, глубина отверстия составляет около 260mm, поэтому требуется сканирование по участкам. Текущая высота H разных участков сканирования различна и может быть измерена кодером в направлении глубины отверстия. После завершения сканирования 2D-данные (x,z) из разных отсканированных участков преобразуются в 3D-данные в системе координат O2XYZ после вышеуказанного расчета.
После сканирования всего отверстия координаты каждой точки 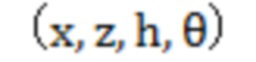 проектируются на
проектируются на 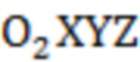 для получения трехмерного облака точек резьбы в отверстии. Процесс сбора, построения и идентификации данных показан на фиг.3.
для получения трехмерного облака точек резьбы в отверстии. Процесс сбора, построения и идентификации данных показан на фиг.3.
Шаг 3: Предварительная обработка 3D-данных облака точек.
Как показано на фиг. 4.
Шаг 3.1 - построить k-окрестность для полученных данных облака точек и вычислить вектор нормали облака точек.
Провести оценку вектора нормали облака точек с помощью метода PCA (PrincipalComponentsAnalysis, Анализ Главных Компонентов).
Задать набор данных облака точек 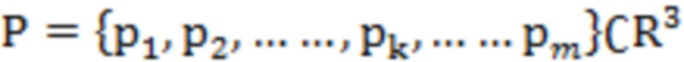 , k-окрестность для точки пробоотбора pi обозначается как N (pi). Для точки пробоотбора pi плоскость наименьших квадратов в k-окрестности определяется как:
, k-окрестность для точки пробоотбора pi обозначается как N (pi). Для точки пробоотбора pi плоскость наименьших квадратов в k-окрестности определяется как:
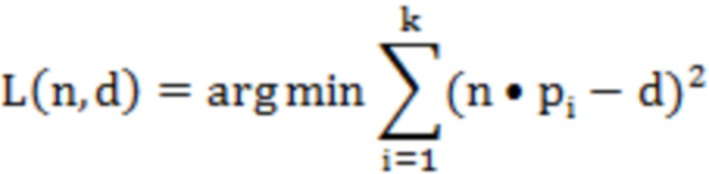
где n - вектор нормали касательной плоскости точки пробоотбора; d - расстояние от точки до плоскости согласования. Решение можно преобразовать в разложение собственных значений положительно полуопределенной ковариационной матрицы C. Собственный вектор, соответствующий наименьшему собственному значению C, является нормальным вектором плоскости:

k-окрестность является набором точек пробоотбора в количестве k, ближайших к точке пробоотбора pi в данных облака точек, математическая форма может быть описана как: предполагается, что набор данных облака точек 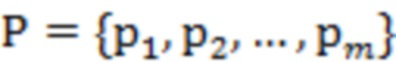 , здесь m- количество облака точек, определить набор k точек пробоотбора, ближайших к точке пробоотбора pi в P, как
, здесь m- количество облака точек, определить набор k точек пробоотбора, ближайших к точке пробоотбора pi в P, как 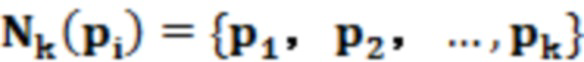 , то есть k-окрестность.
, то есть k-окрестность.
Шаг 3.2 - Вычислить нормальное расстояние от точки пробоотбора до локальной касательной плоскости в ее k-окрестности. Классифицировать точки пробоотбора по характеристикам в соответствии с пороговым значением расстояния и разделить 3D-данные облака точек на гладкую и резкую области.
Текущей точкой является  , выбрать любую точку на плоскости и использовать следующую формулу для вычисления нормального расстояния D локальной касательной плоскости в окрестности k.
, выбрать любую точку на плоскости и использовать следующую формулу для вычисления нормального расстояния D локальной касательной плоскости в окрестности k.
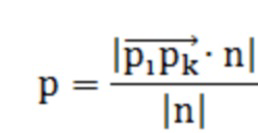
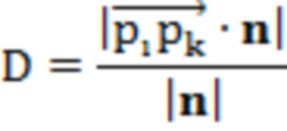
Классифицировать точки пробоотбора по характеристикам в соответствии с пороговым значением расстояния и разделить данные облака точек на гладкую и резкую области. Для предварительной обработки применяются разные алгоритмы, а порог расстояния принимается равным 0.1мм.
В частности, нормальное расстояние от точки пробоотбора до локальной касательной плоскости в окрестности определяется как гладкая область, если оно меньше или равно пороговому значению, и резкая область, если оно больше порогового значения. Алгоритм предварительной обработки см. Шаг 3.
Шаг 3.3 - Провести фильтрацию и обесшумливание с использованием взвешенного локального оптимального алгоритма проецирования и алгоритма двусторонней фильтрации для гладкой и резкой областей соответственно.
Для фильтрации и обесшумливания резкой области используется алгоритм двусторонней фильтрации. В частности, используется следующая формула:
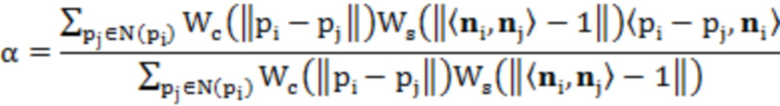
где pi - текущие обрабатываемые точки в наборе облаков точек; pj - точки в окрестности pi; ni, nj - векторы нормали pi, pj соответственно; α- коэффициент двусторонней фильтрации; Wc - гауссовая керн-функция в пространственной области; Ws - гауссовая керн-функция в частотной области.
Данные облака точек после фильтрации определяются следующим образом:

здесь n - вектор нормали к касательной плоскости точки пробоотбора, 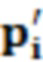 -облако точек после фильтрации.
-облако точек после фильтрации.
Двусторонняя фильтрация как нелинейный фильтр может одновременно достигать результата сохранения краев, обесшумливания и сглаживания обесшумливания. Его основной принцип заключается в использовании метода средневзвешенной величины для расчета координат данной точки с использованием средневзвешенной величины координат точек области, средневзвешенной величины, основанной на распределении по Гауссу, и учитывает не только евклидовое расстояние между координатными точками, но и разность излучения в области, где расположена измеряемая точка.
Провести фильтрацию и обесшумливание с использованием взвешенного локального оптимального алгоритма проецирования для гладкой области, конкретно в следующем:
использовать локальную информацию для локального улучшения данных облака точек. Путем введения весовой функции плотности создать наборы точек с более равномерным распределением, улучшить равномерность распределения облаков точек и гладкость поверхности, при этом используется следующая итерационная формула:
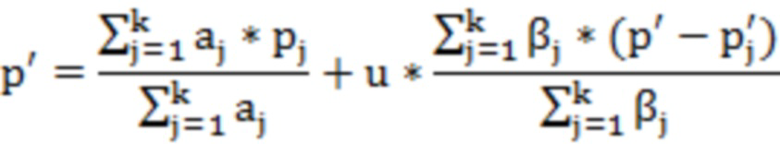
где u - константа (принимается 0,45), p - самое исходное положение облака точек, 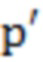 - новое положение после итерации,
- новое положение после итерации,  - количество соседних вершин (принимается 16),
- количество соседних вершин (принимается 16), 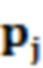 - текущая точка пробоотбора исходного облака точек,
- текущая точка пробоотбора исходного облака точек,  - выходное значение после итерационной операции точки пробоотбора;
- выходное значение после итерационной операции точки пробоотбора;
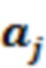 и
и 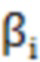 - соответствующие весовые коэффициенты, расчетная формула следующая:
- соответствующие весовые коэффициенты, расчетная формула следующая:
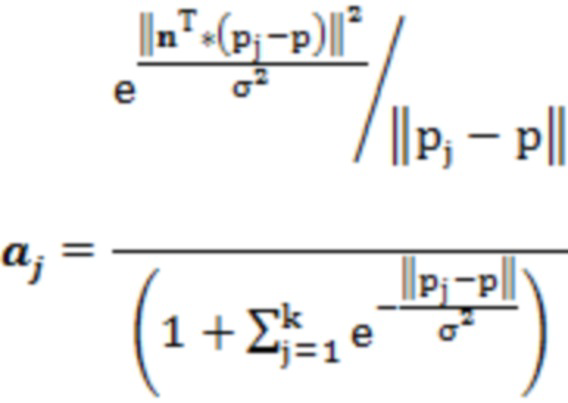
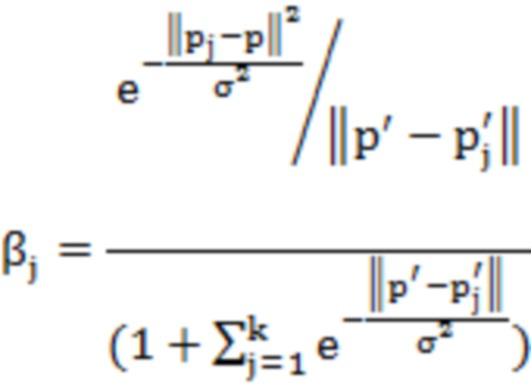
где σ - стандартное отклонение текущей точки из облака точек в окрестности, e - естественная константа.
Шаг 4 - Сжатие 3D-данныхоблака точек по алгоритму.
Сжатие данных - это удаление лишних точек с сохранением геометрических характеристик облака точек. Конкретный алгоритм заключается в использовании метод пробоотбора кривизны, а именно сохранять больше точек для выделения особенностей целевого объекта в областях с более сложным изменением кривизны и меньше точек в областях с относительно плавным изменением кривизны.
Во-первых, с помощью метода сферического линейного уравнения, основанного на методе наименьших квадратов, провести оценку кривизны 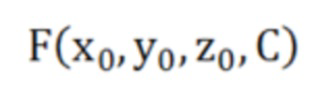 данных облака точек после фильтрации и обесшумливания (шаг 3) по следующей формуле:
данных облака точек после фильтрации и обесшумливания (шаг 3) по следующей формуле:
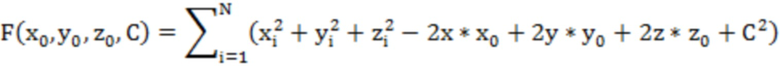
где 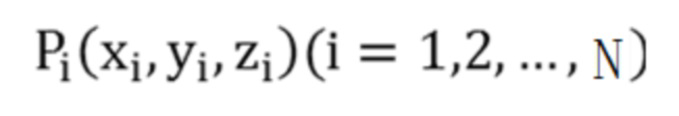 -координаты точек xi, yi, zi на сферической поверхности в системе координат O2XYZ;
-координаты точек xi, yi, zi на сферической поверхности в системе координат O2XYZ;  - координаты центра сферы; R - радиус сферы; С - константа, подлежащая решению;
- координаты центра сферы; R - радиус сферы; С - константа, подлежащая решению;
N обозначает количество сферических точек согласования;
координаты соседних точек из набора облака соседних точек с центром 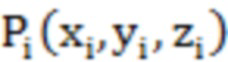 в вышеприведенную формулу подставляются для получения серии систем уравнений, С получается методом наименьших квадратов.
в вышеприведенную формулу подставляются для получения серии систем уравнений, С получается методом наименьших квадратов.
Затем создать локальную систему координат, параллельно перенести исходную точку для получения пространственных координат в новой локальной системе координат, и окончательно решить неизвестные параметры и вычислить кривизну.
Создать локальную систему координат, в качестве исходной точки координат использовать целевую точку, направление ее оси координат совпадет с направлением системы координат системы, выполняется преобразование координат параллельным переносом для получения пространственных координат в новой локальной системе координат, и подставить координаты соседних точек в вышеприведенную формулу для расчета параметров  , C и кривизну ρ целевой точки.
, C и кривизну ρ целевой точки.
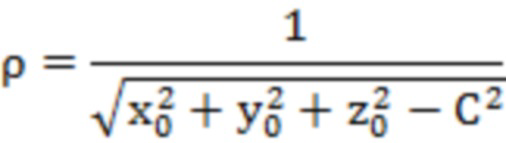
В конце концов провести сравнение значения кривизны с установленным пороговым значением. Если оно больше порогового значения, оно сохраняется, а если оно меньше порогового значения, оно отбрасывается. Установка порога может быть основана на гистограмме кривизны статистических целевых точек, обычно берут 0,5~0,9 от значения в левой части гистограммы, чем больше значение, тем больше сжатия данных, при этом теряется часть низкочастотной информации.
С помощью расчета вышеуказанной гистограммы сначала вычисляется кривизна всех точек в облаке точек, а затем подсчитывается вероятностное распределение разных значений кривизны, которое может быть представлено двухмерным графиком, где горизонтальная ось обозначает значение кривизны, а вертикальная ось - статистическое значение вероятности.
Шаг 5 - Реконструкция 3D-кривой поверхности. Этот шаг заключается в реконструкции полной 3D-модели тестируемого объекта из дискретных данных облака точек.
Как показано на фиг. 5, метод заключается в следующем:
5.1) Во-первых, провести оценку вектора нормали с помощью алгоритма РСА с взвешенной коррекцией.
Взвешенная коррекция, основанная на алгоритме PCA, может снизить чувствительность точек выбросов шума. Выражение плоскости согласования в следующем:
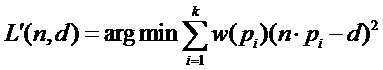
где n - вектор нормали касательной плоскости точки пробоотбора; d - расстояние от точки до плоскости согласования; k - количество точек окрестности;

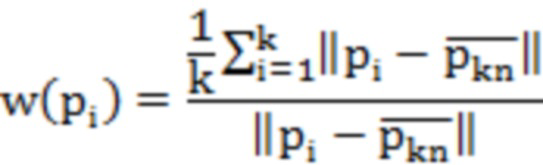
здесь  - центр тяжести k-окрестности
- центр тяжести k-окрестности 
Шаг 5.2) - выполнять разделение облака точек и возвращать набор блоков по результатам оценки.
Для набора данных облака точек P предполагается разделить на К областей, сначала произвольно выбрать К точек из данных облака в качестве начальных центров К разделенных областей, вычислить евклидовое расстояние от каждой точки в облаке точек до центра K начальных разделенных областей, отнести ее к разделенной области, представленную ближайшим начальным разделенной центром, а затем настроить центр каждой разделенной области, повторять вышеуказанный процесс вычисления до тех пор, пока изменятся все центры области, затем остановить итерацию, процесс разделения заканчивается, и выводится результат разделения области.
Шаг регулировки 0,2-2 мм.
Шаг 5.3) - Потом провести поблочное прореживание и повторный отбор проб.
Вычислить кривизну точек в каждой области отдельно по областям блока после разделения облака точек и вычислить среднее значение кривизны в области. Если кривизна точки пробоотбора меньше среднего значения, то данная точка отбрасывается, в противном случае сохраняется отбор проб исходной точки.
Шаг 5.4) - потом вычислить узловую функцию для достижения оптимизации сглаживания.
Оптимизация сглаживания заключается в использовании фильтра Гаусса для достижения результата такого, что не только сохраняются детали локальных характеристик, но и сглаживаются шумовые данные.
Базовая функция узловой функции F0 представлена как:
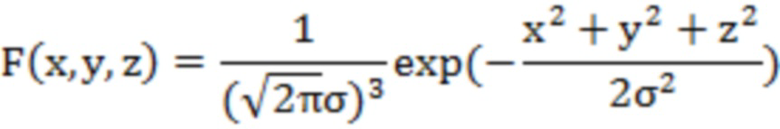
здесь  - стандартное отклонение гауссовской фильтрации, которое обычно принимается
- стандартное отклонение гауссовской фильтрации, которое обычно принимается 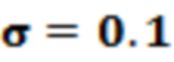 .
.
5.5) Вычислить глубину наибольшего октодерева блоков.
Если установить максимальную глубину глобального октодерева равной Dmax, а минимальную глубину - Dmin, то максимальная глубина локального октодерева каждого блока облака точек может быть выражена как:
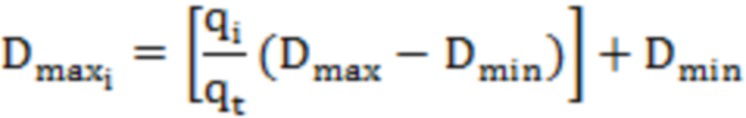
здесь среднее значение кривизны выражается как  ;
;  .
.
5.6) Извлечение изоповерхности для получения представления треугольников изоповерхности в любом вокселе,
где изоповерхность - это одна кривая поверхность в пространстве, функция кривой поверхности которой равна заданному значению.
Если воксель пересекает реконструируемую кривую поверхность, то классифицировать 8 вершин вокселя, чтобы определить, что его вершина распложена вне или внутри изоповерхности. Затем определить метод разделения изоповерхности по состоянию 8 вершин. Правило классификации вершин: если значение данных вершины вокселя больше или равно значению изоповерхности, то вершина определяется как находящаяся вне изоповерхности и отмечается как положительная точка, т.е. 1. Если значение данных вершины вокселя меньше значения изоповерхности, то вершина определяется как находящаяся внутри изоповерхности и отмечается как отрицательная точка, т.е. 0. В связи с тем, что каждый воксель имеет восемь вершин, и каждая вершина имеет два состояния, положительное и отрицательное, поэтому изоповерхности могут пересекаться с вокселем в общей сложности 256 способами. Путем перечисления этих 256 случаев, можно создать таблицу, которую можно использовать для поиска представления треугольников изоповерхностей в любом вокселе.
5.7) Создание сетчатой модели.
По положительному и отрицательному состоянию поля направленного расстояния 8 вершин получаются треугольники, координаты вершин треугольников, то есть точки пересечения края точек вокселя с реконструируемой кривой поверхностью получаются путем линейной интерполяции двух вершин края точек вокселя.
Шаг 6 – Идентификация и измерение дефектов.
6.1) Алгоритм ICP (IterativeClosestPoint) используется для подгонки, чтобы создать целевой функции идентификации дефектов:

где  - облако точек в стандартной модели;
- облако точек в стандартной модели; 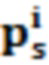 - облако точек, подлежащее подгонке; R - матрица переноса; T - матрица перевода; NP - количество облака точек в стандартной модели.
- облако точек, подлежащее подгонке; R - матрица переноса; T - матрица перевода; NP - количество облака точек в стандартной модели.
Согласно вышеизложенному уравнению вычислить оптимальные R и T методом наименьших квадратов, затем выполняется итерация до тех пор, пока вычисленное значение 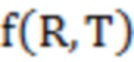 не будет минимальным.
не будет минимальным.
6.2) Провести кластерное разделение и извлечение характеристик дефектных областей.
Вычисляя расстояние от точки до кривой поверхности, можно получить расстояние отклонения от точки измерения до модели облака точек. Определить местоположение дефектов поверхности по значениям расстояния. Среднее значение расстояния отклонения выражается как:
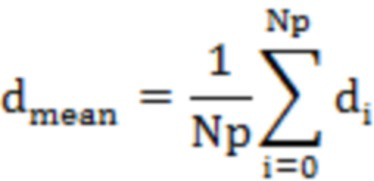
здесь di обозначает расстояние от точки до кривой поверхности модели облака точек.
Определить расстояние отклонения и среднее значение всех точек, сохранить точку xi, соответствующую di, в классе X (определить X как начальное множество точек кластеризации), когда di>dmean, и пройти все точки, чтобы выделить область с большим расстоянием отклонения до поверхности модели облака точек.
6.3) Затем характеризовать дефекты параметрами, и в конечном итоге выводить тип дефектов.
Произвести расчет характерных параметров дефектной области, определить площадь, периметр и соотношение длины к ширине дефекта.
Площадь - это геометрическая характеристика, которая измеряет размер области. Метод расчета в следующем:
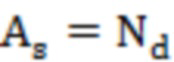
здесь 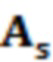 - площадь дефектной области; S - измеренная площадь дефектной области;
- площадь дефектной области; S - измеренная площадь дефектной области;  - количество облаков точек в дефектной области.
- количество облаков точек в дефектной области.
Периметр дефекта - это длина граничной контурной линии, которая окружает дефектную область, и рассчитывается как:
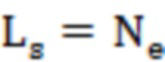
здесь 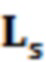 - периметр дефектной области;
- периметр дефектной области; 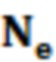 - количество характеристик границы дефектной области.
- количество характеристик границы дефектной области.
Соотношение длины к ширине используется для определения его формы и рассчитывается следующим образом:
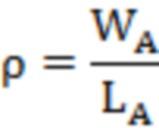
Дефект поверхности резьбы - это область, где измеренный объект сравнивается со стандартной резьбой и большое расстояние отклонения (обычно 0,1 мм) идентифицируется как дефект. Вычислив расстояние от точки до кривой поверхности, получают расстояние отклонения от измеренной точки до стандартной модели облака точек, и по значению расстояния определяют местоположение дефекта. Для классификации типа дефекта необходимо определить характерные параметры области дефекта, включая площадь, периметр, соотношение длины к ширине и округлость области дефекта. На основе характеристик дефектов пользователь может задать условия для просеивания и поиска дефектов.
Часть настоящего изобретения, которая не была подробно раскрыта, относится к известной технологии в данной области.
Несмотря на то что конкретный способ осуществления настоящего изобретения описан выше, чтобы облегчить его понимание техническими специалистами в данной технической области, должно быть ясно, что данное изобретение не ограничивается объемом конкретного способа осуществления, для обычных технических специалистов в данной технической области, пока различные вариации находятся в пределах сущности и объема настоящего изобретения, определенных в прилагаемой формуле изобретения, и являются очевидными, все изобретения и создания, использующие концепцию настоящего изобретения, находятся под защитой.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ И СИСТЕМА ОБНАРУЖЕНИЯ И СОПРОВОЖДЕНИЯ ДВИЖУЩИХСЯ ОБЪЕКТОВ НА ОСНОВЕ ДАННЫХ ТРЕХМЕРНОГО ДАТЧИКА | 2016 |
|
RU2656711C2 |
| ТРЕХМЕРНЫЙ СКАНЕР С ОБРАТНОЙ СВЯЗЬЮ ПО СБОРУ ДАННЫХ | 2019 |
|
RU2793584C2 |
| СИСТЕМА КОНТРОЛЯ ПУТИ | 2020 |
|
RU2810283C2 |
| СПОСОБ И СИСТЕМА ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ГЕОМЕТРИЧЕСКОГО ПОЛОЖЕНИЯ КОЛЕС ТРАНСПОРТНОГО СРЕДСТВА ПО ДАННЫМ ТРЕХМЕРНОГО СКАНИРОВАНИЯ ПОВЕРХНОСТЕЙ КОЛЕС ТРАНСПОРТНОГО СРЕДСТВА | 2020 |
|
RU2754961C1 |
| Способ контроля технического состояния несущих железобетонных и/или каменных строительных конструкций | 2023 |
|
RU2840684C1 |
| ТРЕХМЕРНЫЙ СКАНЕР С ОБРАТНОЙ СВЯЗЬЮ ПО СБОРУ ДАННЫХ | 2019 |
|
RU2767590C2 |
| СПОСОБ ВЕДЕНИЯ ИЗМЕРЕНИЙ В ХОДЕ КОНТРОЛЯ МЕСТНЫХ ОСТАТОЧНЫХ ДЕФОРМАЦИЙ КОРПУСА СУДНА | 2017 |
|
RU2689897C1 |
| СИСТЕМА И СПОСОБ СКАНИРОВАНИЯ И КОПИРОВАНИЯ | 2004 |
|
RU2368091C2 |
| Метод совместной калибровки лидара и камеры | 2021 |
|
RU2837595C2 |
| СПОСОБ ОЦЕНКИ СТРУКТУРНЫХ ИЗМЕНЕНИЙ ОБРАЗЦА МАТЕРИАЛА В РЕЗУЛЬТАТЕ ВОЗДЕЙСТВИЯ НА ОБРАЗЕЦ | 2014 |
|
RU2673774C2 |




Изобретение относится к области ремонта оборудования АЭС, конкретно касается трехмерной реконструкции резьбы отверстий под шпильки главного разъема корпуса реактора и метода автоматической идентификации дефектов. Сущность: осуществляют сканирование для получения двумерных координат поверхности резьбы; затем синтез трехмерных координатных данных, т.е. трехмерных данных облака точек из информации о двухмерных координатах поверхности резьбы, угловых данных и данных осевого положения сканирующего устройства; после чего предварительную обработку трехмерных данных облака точек, определение нормальных векторов трехмерных данных облака точек с разделением их на гладкие и резкие области, затем фильтрацию и обесшумливание соответственно; затем оптимизацию трехмерных данных облака точек, сохраняя данные, превышающие пороговое значение; после чего выполнение трехмерной реконструкции кривой поверхности контролируемого объекта и создание сетчатой модели; затем идентификацию и измерение дефекта, характеризование дефекта параметрами и вывод типа дефекта. Технический результат: возможность быстро и точно контролировать резьбу в трехмерном масштабе, идентифицировать дефекты и вычислять размеры дефектов, выводить результаты контроля, а также полностью автоматически выполнить сбор, анализ и обработку данных всех отверстий, при этом время выполнения такой операции на одном отверстии не более 5 мин. 11 з.п. ф-лы, 5 ил.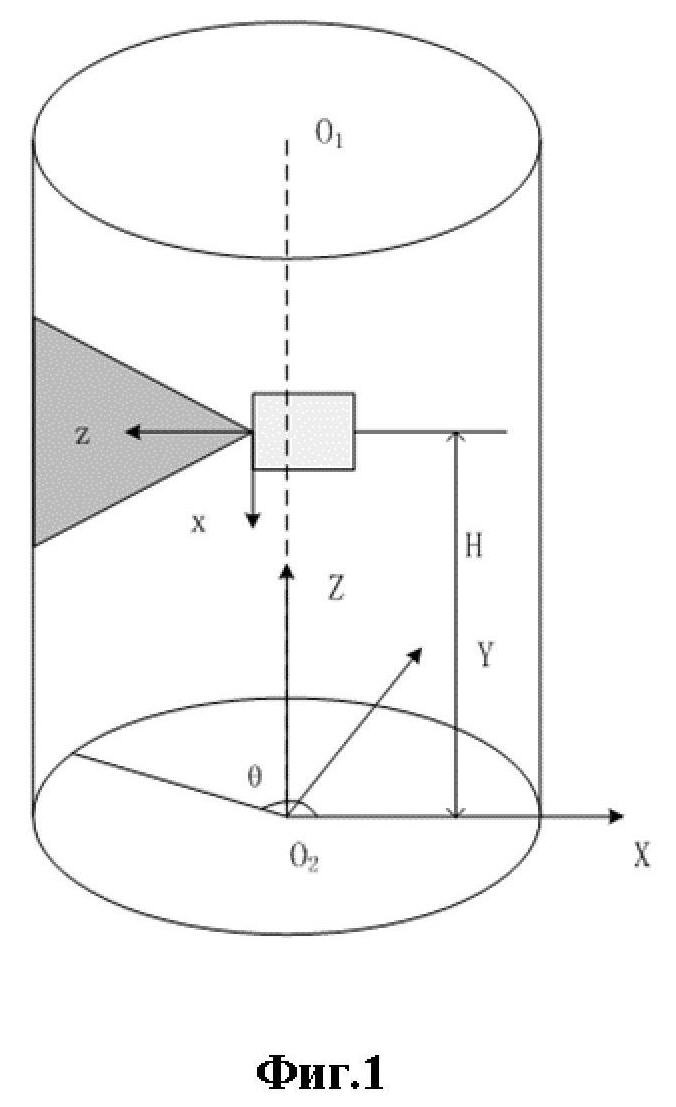
1. Способ трехмерной реконструкции резьбы отверстия под шпильки главного разъёма корпуса реактора (КР) и автоматической идентификации дефектов, характеризующийся тем, что он включает следующие шаги:
шаг 1) - сканирование для получения двумерных координат поверхности резьбы;
шаг 2) - синтез трехмерных координатных данных, т.е. трехмерных данных облака точек из информации о двухмерных координатах поверхности резьбы, угловых данных и данных осевого положения сканирующего устройства;
шаг 3) - предварительная обработка трехмерных данных облака точек, определение нормальных векторов трехмерных данных облака точек с разделением их на гладкие и резкие области, затем фильтрация и обесшумливание соответственно;
шаг 4) - оптимизация трехмерных данных облака точек, сохраняя данные, превышающие пороговое значение;
шаг 5) - выполнение трехмерной реконструкции кривой поверхности контролируемого объекта и создание сетчатой модели;
шаг 6) - идентификация и измерение дефекта, характеризование характеристик дефекта параметрами и вывод типа дефекта.
2. Способ по п.1, характеризующийся тем, что шаг 1) выполняется следующим образом:
сначала создают две системы координат: одна - система координат oxz, в которой исходной точкой является опорная точка самого сканирующего устройства, а измеренные двумерные данные поверхности резьбы являются координатами точки в системе координат oxz, характеризуемые как (x, z); другая - система координат резьбового отверстия O2XYZ, где O2 обозначает центр окружности в нижней плоскости отверстия, Z - направление оси резьбового отверстия вверх, X - направление тангенциальное по часовой стрелке к центру резьбового отверстия на главном разъёме КР, Y - направление, указывающее на центр КР, это направление оси определяют в соответствии с правилом правой руки; H представляет собой высоту сканирующего устройства относительно дна резьбового отверстия, а θ представляет собой угол проекции сканирующего устройства на плоскость OXY в текущей системе координат;
после выполнения маркировки измеряемых резьбовых отверстий, позиционирования и установки сканирующего устройства сканирующая головка опускается до начального участка резьбы, вращается на один круг и одновременно происходит сбор 2D данных, сканирующая головка поднимается до верха отверстия, затем сканирующее устройство перемещается для продолжения сканирования всех остальных резьбовых отверстий и получения информации о 2D координатах всех резьбовых отверстий.
3. Способ по п. 2, характеризующийся тем, что указанное сканирующее устройство представляет собой линейный структурированный световой сканер, который устанавливают на корпусе машины для позиционирования, причем корпус машины для позиционирования перемещают вдоль положения различных отверстий для винтов на поверхности фланца корпуса реактора для осуществления сканирования каждого отверстия для винтов, при этом при достижении положения одного отверстия с определенным номером корпус машины для позиционирования сначала позиционируют для обеспечения фиксации положения корпуса машины относительно корпуса реактора при сканировании.
4. Способ по п. 2, характеризующийся тем, что, перед тем как сканирующая головка поднимется до верха, необходимо определить, достигает ли сканирующая головка до дна отверстия, причем если она не достигает верха, то сканирующая головка опускается, а затем снова вращается на один круг, и 2D-данные собираются одновременно, пока она не достигнет дна.
5. Способ по п. 1, характеризующийся тем, что шаг 2) выполняется следующим образом:
двумерные данные поверхности резьбы, координаты которых характеризуются как (x, z) в системе координат oxz, а расстояние между точкой отсчета сканирующего устройства и центром резьбового отверстия является константой, обозначаемой как D, можно получить 3D-данные облака точек, т.е. координаты (x,z) в системе координат O2XYZ, обозначаемым как:
 ,
,
 ,
,
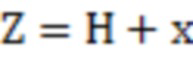 .
.
6. Способ по п. 1, характеризующийся тем, что шаг 3) выполняется следующим образом:
шаг 3.1) построить k-окрестность для полученных данных облака точек, вычислить вектор нормали облака точек, провести оценку вектора нормали облака точек с помощью метода PCA и получить множество k точек пробоотбора, ближайших к точке пробоотбора pi в данных облака точек;
шаг 3.2) вычислить нормальное расстояние от точки пробоотбора до локальной касательной плоскости в ее k-окрестности, классифицировать точки пробоотбора по характеристикам в соответствии с пороговым значением расстояния и разделить 3D-данныех облака точек на гладкую и резкую области, при этом нормальное расстояние от точки пробоотбора до локальной касательной плоскости в окрестности определяется как гладкая область, если оно меньше или равно пороговому значению, и резкая область, если оно больше порогового значения;
шаг 3.3) фильтрация и обесшумливание гладкой и острой областей соответственно.
7. Способ по п. 6, характеризующийся тем, что острая область фильтруется и обесшумливается с помощью алгоритма двусторонней фильтрации, в частности используется следующая формула:
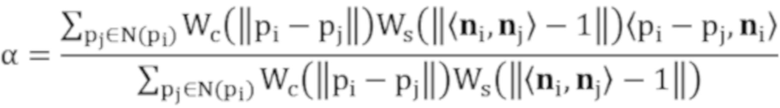 ,
,
где pi - текущая обрабатываемая точка в наборе облаков точек, pj - точка в pi-окрестности, ni и nj - нормальные векторы pi и pj соответственно, α - коэффициент двусторонней фильтрации, Wc - гауссова керн-функция в пространственной области, Ws -гауссова керн-функция в частотной области;
отфильтрованные данные облака точек выражаются как
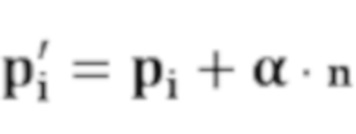 ,
,
где n - вектор нормали к касательной плоскости выбранных точек, α - положение отфильтрованного облака точек.
8. Способ по п. 6, характеризующийся тем, что для фильтрации и обесшумливания гладкой области используется алгоритм взвешенной локальной оптимальной проекции, в частности:
используя локальную информацию для локального улучшения данных облака точек, путем введения весовой функции плотности для получения более равномерно распределенного набора точек, равномерность распределения облака точек и гладкость поверхности улучшается с помощью итерационной формулы
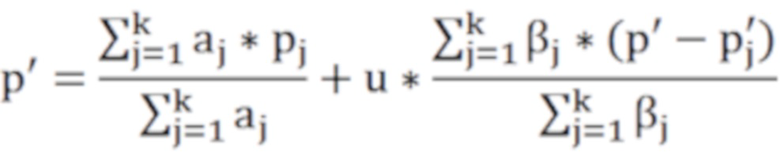 ,
,
 ,
,
 ,
,
где u - константа, p - самое исходное положение облака точек, p' - новое положение после итерации,  - количество соседних вершин, pj - текущая пробоотборная точка исходного облака точек,
- количество соседних вершин, pj - текущая пробоотборная точка исходного облака точек,  - выводное значение точки пробоотбора после итерационной операции;
- выводное значение точки пробоотбора после итерационной операции; 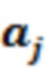 и
и 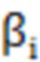 - соответствующие весовые коэффициенты, σ - стандартное отклонение текущей точки облака точек в окрестности, e - естественная константа.
- соответствующие весовые коэффициенты, σ - стандартное отклонение текущей точки облака точек в окрестности, e - естественная константа.
9. Способ по п. 1, характеризующийся тем, что шаг 4) выполняется следующим образом:
во-первых, кривизна облачных данных точек  после фильтрации и обесшумливания на шаге 3) оценивается с помощью сферического линейного уравнения на основе метода наименьших квадратов, используя следующую формулу:
после фильтрации и обесшумливания на шаге 3) оценивается с помощью сферического линейного уравнения на основе метода наименьших квадратов, используя следующую формулу:
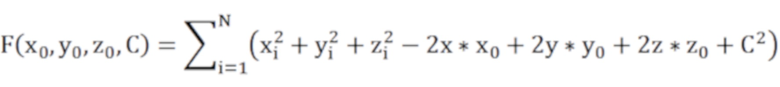 ,
,
где 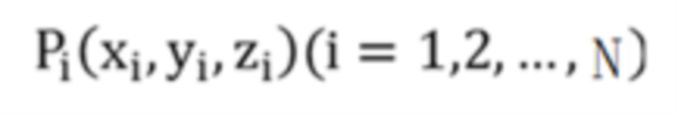 - координаты точек xi, yi, zi на сферической поверхности в системе координат O2XYZ,
- координаты точек xi, yi, zi на сферической поверхности в системе координат O2XYZ, 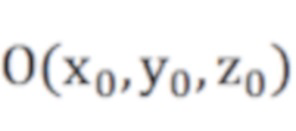 - координаты центра шара, R - радиус шара, C - решаемая константа, N - количество точек подогнанной сферической поверхности, координаты соседних точек в наборе облака соседних точек с центром подставляются в вышеприведенную формулу для получения серии систем уравнений, а C определяется методом наименьших квадратов;
- координаты центра шара, R - радиус шара, C - решаемая константа, N - количество точек подогнанной сферической поверхности, координаты соседних точек в наборе облака соседних точек с центром подставляются в вышеприведенную формулу для получения серии систем уравнений, а C определяется методом наименьших квадратов;
затем создают локальную систему координат, параллельно переносят исходную точку для получения пространственных координат в новой локальной системе координат и, наконец, вычисляют кривизну путем вычисления неизвестных параметров;
наконец, значение кривизны сравнивают с величиной установленного порогового значения, если значение больше порога, оно сохраняется, если оно меньше порога, то отбрасывается.
10. Способ по п. 1, характеризующийся тем, что шаг 5) выполняют следующим образом:
шаг 5.1) выполнение оценки нормального вектора со взвешенной коррекцией
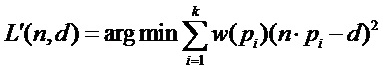
где n - вектор нормали касательной плоскости выборочных точек, d обозначает расстояние от точки до подогнанной плоскости, k - количество точек окрестности, pi - текущая точка пробоотбора, w(pi) - взвешенное значение, выражение которого следующее:
 ,
,
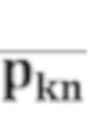 - центр тяжести k - окрестности;
- центр тяжести k - окрестности;
шаг 5.2) разбить облака точек и вернуться к разбитому на куски набору,
набор облачных данных точек P рассчитывают разбить на K-количество областей, сначала произвольно выбирают K-количество точек m из данных облака точек в качестве исходных центров K-количества разбиваемых областей, вычислить Евклидово расстояние от каждой точки из облака точек до K-количество исходных центров разбивания, распределить их в разбиваемые области, представленные ближайшими начальными центрами разбивания, затем настроить центр каждой разделённой области, итерировать вышеуказанный процесс вычисления до тех пор, пока центры всех областей не перестанут изменяться, затем прекратить итерацию, процесс разбивания заканчивается, и выводить результаты разбивания областей;
шаг 5.3) выполнить поблочное прореживание и повторный пробоотбор,
вычислить кривизну точек в каждой области отдельно по разделенным областям блока, вычислить кривизну точки в каждой области отдельно и среднее значение кривизны в области, если кривизна точки пробоотбора меньше среднего значения, то данная точка отбрасывается, в противном случае сохраняется отбор проб исходной точки;
шаг 5.4) вычислить узловую функцию для достижения оптимизации сглаживания;
фундаментальная функция узловой функции F0 выражается как
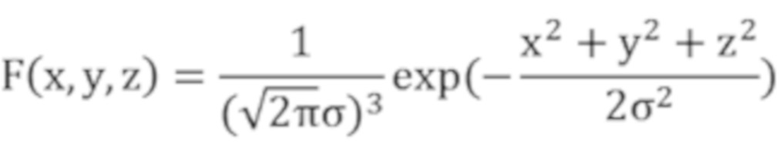 ,
,
где σ - стандартное отклонение гауссовой фильтрации;
вычисляют глубину максимального восьмеричного дерева блоков,
если задать максимальную глубину глобального октодерева равной Dmax, а минимальную глубину - Dmin, то максимальная глубина локального октодерева каждого блока облака точек выражается как
 ,
,
где среднее значение кривизны выражается как
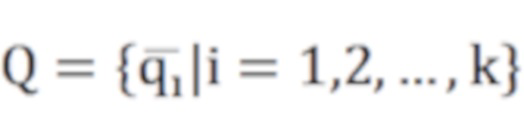 ,
, ;
;
шаг 5.6) извлечение изоповерхности для получения отображения изоповерхности треугольниками в любом вокселе;
определяют, лежат ли его вершины вне или внутри изоповерхности, а затем определяют схему разбиения изоповерхности в соответствии с состоянием вершин;
если значение данных вершины вокселя больше или равно значению изоповерхности, то вершина определяется как находящаяся вне изоповерхности и отмечается как положительная точка, т.е. 1, если значение данных вершины вокселя меньше значения изоповерхности, то вершина определяется как находящаяся внутри изоповерхности и отмечается как отрицательная точка, т.е. 0;
каждый воксель имеет в общей сложности 8 вершин, и каждая вершина имеет два состояния, положительное и отрицательное, а изоповерхность может пересекать воксель в общей сложности 256 способами, образуя отображение изоповерхности треугольниками в любом вокселе;
шаг 5.7) создание сетчатой модели,
по положительному и отрицательному состоянию поля направленного расстояния 8 вершин получаются треугольники, координаты вершин треугольников, то есть точки пересечения края точек вокселя с реконструируемой кривой поверхностью, получаются путем линейной интерполяции двух вершин края точек вокселя.
11. Способ по п. 1, характеризующийся тем, что шаг 6) выполняется следующим образом:
шаг 6.1) создание целевой функции идентификации дефектов:
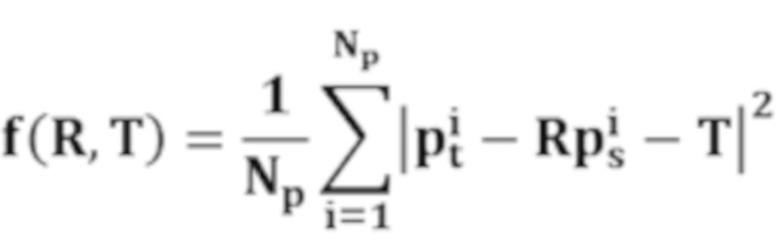 ,
,
где 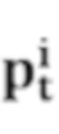 - облако точек в стандартной модели,
- облако точек в стандартной модели, 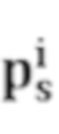 - облако точек, подлежащее выравниванию (подгонке), R - матрица поворота, T - матрица переноса; NP - количество облаков точек в стандартной модели; оптимальные значения R и T рассчитываются методом наименьших квадратов; затем выполняется итерация до тех пор, пока рассчитанное значение f(R,T) не будет минимальным;
- облако точек, подлежащее выравниванию (подгонке), R - матрица поворота, T - матрица переноса; NP - количество облаков точек в стандартной модели; оптимальные значения R и T рассчитываются методом наименьших квадратов; затем выполняется итерация до тех пор, пока рассчитанное значение f(R,T) не будет минимальным;
шаг 6.2) выполнение кластерного разбивания дефектных областей и извлечение характеристики,
определение местоположения дефектов поверхности на основе значений расстояния,
при этом среднее значение расстояний отклонения выражается как
 ,
,
где di представляет собой расстояние от точки до кривой поверхности модели облака точек;
оценивать величину расстояния отклонения всех точек и среднего значения, сохранить точку xi, соответствующую di при di>dmean, в классе X, пройти все точки и таким образом выделить области с большим расстоянием отклонения от поверхности модели облака точек;
шаг 6.3) характеристика дефекта выражается параметрами, определить площадь, периметр и соотношение длины к ширине дефекта, и, наконец, выводить тип дефектов.
12. Способ по п. 11, характеризующийся тем, что:
площадь дефекта - это геометрическая характеристика по результатам измерения размера области и рассчитывается как
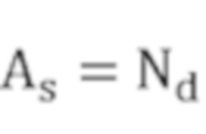 ,
,
где As - площадь области дефекта, S - измеренная область дефекта, а Nd - количество облаков точек в области дефекта;
периметр дефекта - это длина линии контура границы, окружающего дефектную область, рассчитывается как
 ,
,
где Ls - периметр области дефекта, а Ne - количество характеристик границы области дефекта;
соотношение длины к ширине дефекта используется для определения его формы и рассчитывается следующим образом:
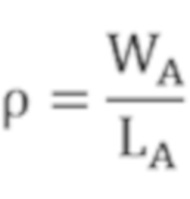 .
.
| CN 111710447 A, 25.09.2020 | |||
| CN 111795661 A, 20.10.2020 | |||
| Двигатель постоянного тока | 1930 |
|
SU32026A1 |
| Способ трехмерной реконструкции поверхности образца по изображениям, полученным в растровом электронном микроскопе | 2016 |
|
RU2704390C2 |
Авторы
Даты
2023-03-07—Публикация
2022-04-28—Подача