Изобретение относится к измерительной технике и может быть использовано для определения числа Френеля оптический системы, характеризующего , ее дифракционное качество.
Цель изобретения - повьшение точности, а также упрощение процесса измерений.
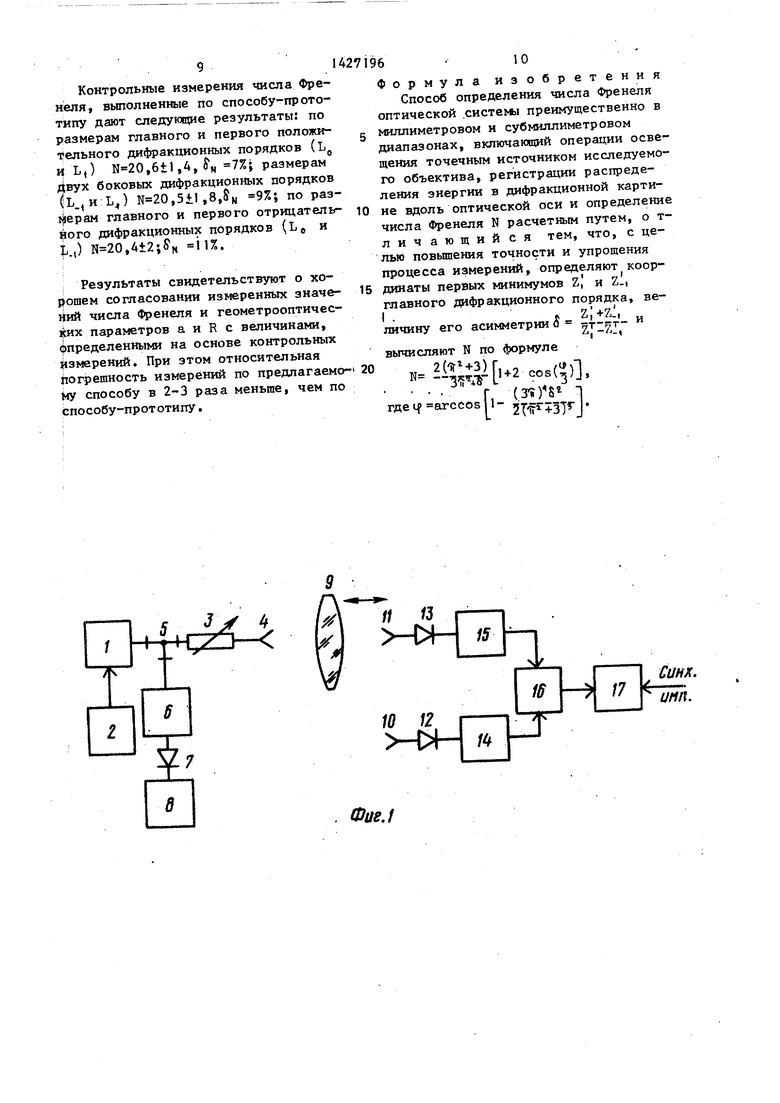
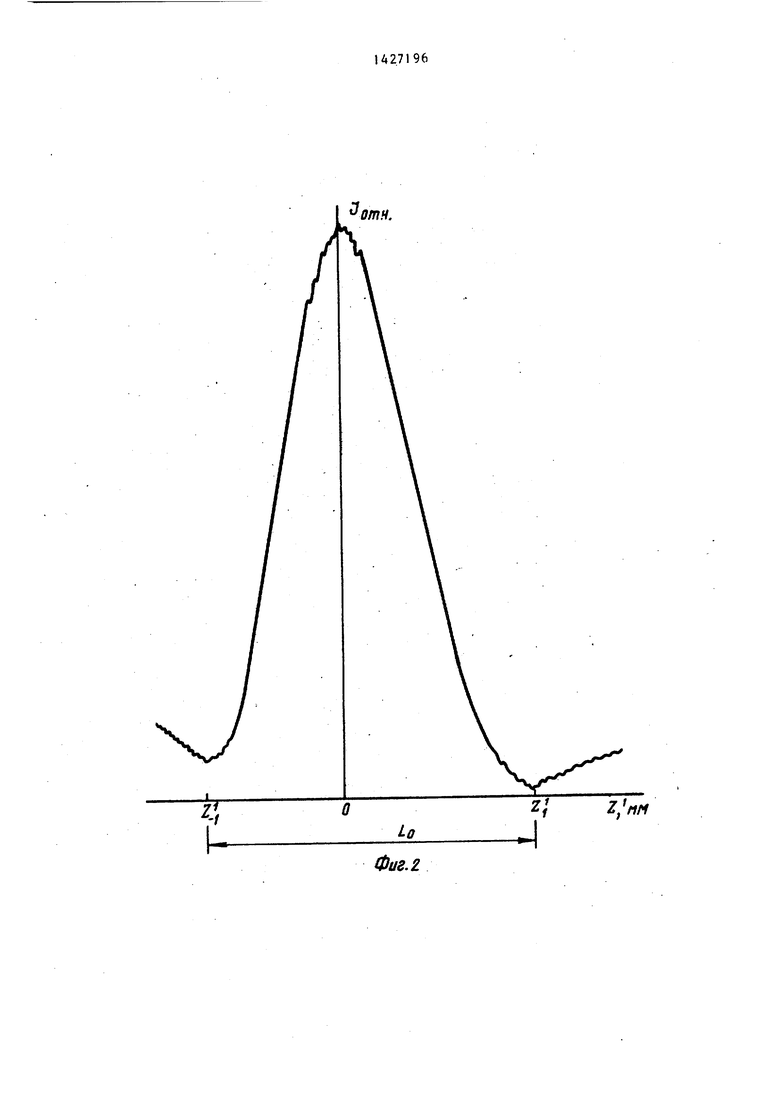
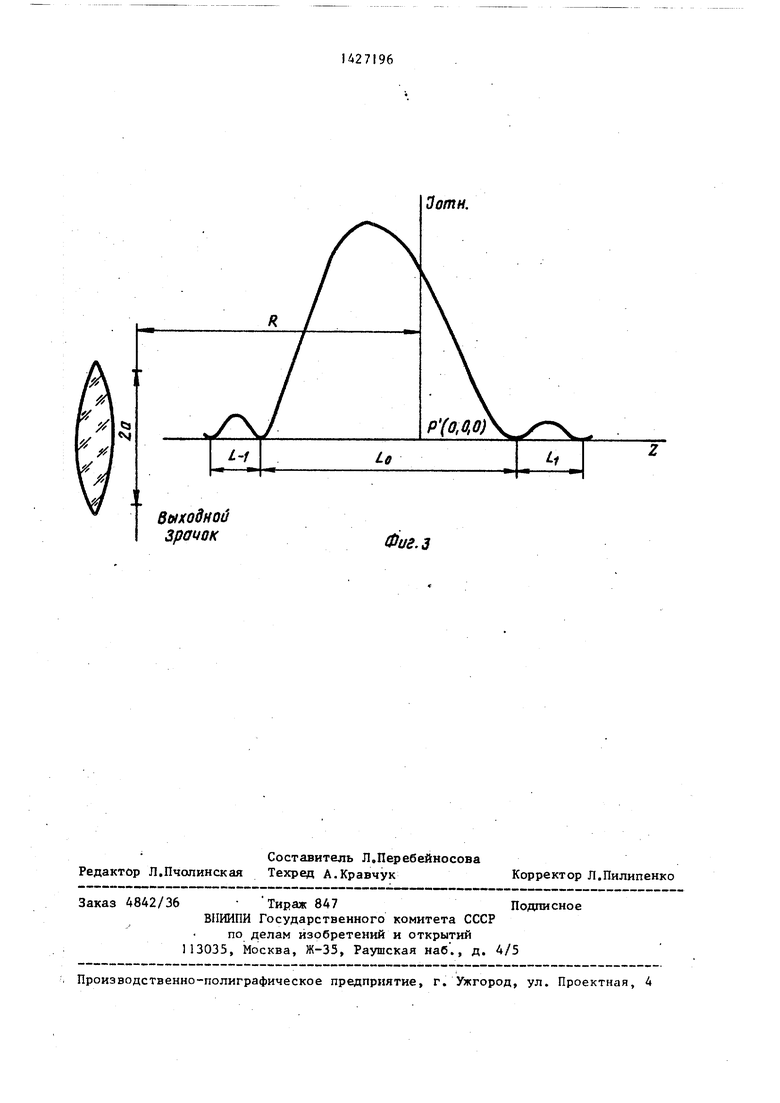
На фиг, 1 изображена схема устрой- ю ства для реализации предложенного способаJ на фиг, 2 и 3 - экспериментально снятые кривые l(Z),
Устройство содержит передающий блок, исследуемую радиооптическую15
систему и приемный блок,
Передающий блок состоит из СВЧ-ге нератора 1 миллиметрового диапазона, генератора 2 модулирующего сигнала,. 1 аттенюатора 3, передающей антенны 4, ,20 направленного ответвителя 5, волномера 6 , детекторной головки 7 и осциллографа 8,
Приемный блок включает в себя антенну 10 опорного канала, приемную аи-25 теину 11, детекторные головки 12 и 13, селективные усилители 14 и 15, преобразователь напряжения 16. и самописец 17, I30
Способ осуществляется следующим образом,
СВЧ-сигнал с генератора 1, промо- дулированный по амплитуде низкочастотным сигналом (порядка Ю кГц) с гене- ратора 2, через направленный ответвитель 5 и аттенюатор .3 поступает в ан- I ----
тенну 4 и излучается в открытое пространство. Одновременно часть сигнаа через направленный ответвитель по- Q дается на волномер 6, К вькоду волномера подключена детекторная головка 7, сигнал- с которой поступает в канал У осциллографа 8, Элементы 6-8 измеряют рабочую датину волны СВЧ-ге- дс нератора. Если контролируемая оптическая система 9 рассчитана для работы на конечных расстояниях (типа про- екционгых оптических систем или систем с небольшим увеличением), то в . качестве передающей антенны 4 можно использовать открытый конец волновода стандартного сечения, раскрыв которого совмещен с плоскостью предметов (ПП), В случае проверки системы, .. рассчитанной на бесконечность,(типа i фотообъектива), может быть использована антенна в виде пирамидального рупора с корректирующей линзой, создающая квазиплоскую электромагнитную волну. Радиооптическая система 9 фор мирует изображение точечного источника в виде сложного дифракционного- распределения. Вдоль оптической оси с помощью специальной системы сканирования перемещается ггриемная антенна П, также выполненная в :виде открытого среза прямоугольного волновода стандартного сечения, С антенны 11 СВЧ-сигнал поступает на детекторную головку 13 и далее на селективный усилитель 15, который настроен на частоту модулирующего сигнала, С выхода усилителя низкочастотньй сигнал поступает на вход преобразователя 16 .нап$ яжения , На другой вход преобразователя поступает опорный сигнал той же частоты, прошедший через приемную антенну 10, детекторную головку 12 и селективньй усилитель 14, С выхода преобразователя напряжения сигнал подается на вход У двух координатного; самописца 17, на вход X которого одновременно поступает сигнал с датчика положения сканирующей системы.
Перо самописца вычерчивает в выбранном масштабе кривую дифракционного распределения интенсивности вдоль оптической оси. Дальнейшее измерение координат первых минимумов и определение асимметрии распределения производится на полученном графике с учетом масштабных соотношений,
Поле волны, сформированной точечным источником и прошедшей через исследуемую систему, сканируют вдоль оптической оси, регистрируют распределение энергии в области главного дифракционного порядка и определяют величину асимметрии S, являющуюся характеристикой формы указанного распределения:
К z; +z:,
. У 1
где Z, и Z., - координаты (с учетом
знака) первых минимумо дифракционного распредления в декартовой системе координат, начало совпадает с максимумом главного диракционного порядка. По найденному значению S определяют число Френеля системы и ее гео- метрооптические параметры:
N-
-ir
1+2 cos(
1.
2ц
2kR N+Jic



| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения числа Френеля оптической системы (его варианты) | 1984 |
|
SU1224644A1 |
| Способ определения разрешающей способности оптической системы | 1988 |
|
SU1597655A1 |
| Голографическое сканирующее устройство (его варианты) | 1983 |
|
SU1179255A1 |
| СПОСОБ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЯ С СУБДИФРАКЦИОННЫМ РАЗРЕШЕНИЕМ | 2013 |
|
RU2533502C1 |
| Способ измерения полей рассеяния и дифракции на телах | 1988 |
|
SU1538151A1 |
| Способ амплитудного двухмерного пеленгования | 2016 |
|
RU2620130C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ВОЛНОВЫХ АБЕРРАЦИЙ ОПТИЧЕСКОЙ СИСТЕМЫ | 2018 |
|
RU2680657C1 |
| СПОСОБ И СИСТЕМА ГОЛОГРАФИЧЕСКОЙ ЗАПИСИ И ВОСПРОИЗВЕДЕНИЯ ЗВУКОВОЙ ИНФОРМАЦИИ | 2000 |
|
RU2160471C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАПРАВЛЕНИЯ НА ГИДРОАКУСТИЧЕСКИЙ МАЯК-ОТВЕТЧИК ПО ГОРИЗОНТАЛЬНОМУ И ВЕРТИКАЛЬНОМУ УГЛУ | 2011 |
|
RU2492498C2 |
| СПОСОБ ОБРАБОТКИ ИНФОРМАЦИИ В ЛАЗЕРНОМ КОГЕРЕНТНОМ ЛОКАТОРЕ С МАТРИЧНЫМ ФОТОПРИЕМНИКОМ | 2007 |
|
RU2354994C1 |

Изобретение относится к изйери- тельной технике. Цель изобретения - повышение точности, а также упрощение процесса измерений. Для этого поле волны, сформированной точечным источником и прошедшей через исследуемую систему, сканируют вдоль оптической оси, регистрируют распределение энергии в области главного дифракционного порядка и определяют величину асимметрии о , являющуюся характеристикой формы распределения. По найденному значению 8 определяют число Френеля системы и ее геометрооптичес- кие параметры. 3 ил. с 
arccos
Г. (37)V 1 2Tf
Рассмотрим поведение дифракционного распределения интенсивности в фо- Кельном объеме дифракционно ограниченной оптической системы с малым числом Френеля.
На фиг. 3 начало декартовой системы координат совпадает с параксиальным изображением Р осевого точечного монохроматического источника и находится на расстоянии R от выходного зрачка оптической системы, соответствующем радиусу опорной сферы, а ось Z направлена вдоль оптической оси. Точка Q представляет собой произвольную точку, лежащую в окрестно- ,сти параксиального фокуса. Известно, что относительное распределение ин- тейсивности вдоль оптической оси может быть описано функцйональкой зависимостью вида:
и Н|иЬ|т -сов( ьК.),(1)
где N - - число Френеля (определяет количество зон Френеля на выходном зрачке при наблюдении из параксиально- го фокуса Р ); Z - координата точки Q. Данное дифракционное распределение имеет ряд характерных признаков, которые выражены тем сильнее, чем меньше число Френеля. Во-первых, главный максимум дифракционного распределения смещен относительно параксиального фокуса в направлении выходного зрачка оптической аисте. Его координата может быть приближенно определена из решения трансцендентного уравнения:
1
-iJZ-- 2)
2
.(Г , I RSfEZ - - r
/ n /:,„, X
sfz;
12E
и равна - (для ,205)
Координаты минимумов интенсивности определяются из выражений .
2kR
K- N:2k
Q
5
0 5
0
5 0 5
0
где Z - координаты минимумов, лежащих справа от главного максимума (в области ); Z - координаты минимумов, лежащих слева от главного максимума (в области ); ,2, - порядок минимума.
Из (-3) следует, что количество минимумов справа определяется чисNлом Френеля, т.е. k . Например,
для существования первого минимума (в области Z 0) необходимо, чтобы выполнялось условие для второго минимума - (условие существования первого положительного максимума) и т.д.
Из сказанного вытекает второй характерный признак, которьй заключается в следующем. Оптическая система с числом Френеля N 2 перестает быть фокусирующей, становится направля- Joщeй структурой, формируя узкий волновой пучок (наподобие гауссова), вытянутый вдоль оптической оси. Ак- сиальное распределение интенсивности вдоль оси осциллирует до точки главного максимума, а затем асимптотически стремится к нулю.
Третьей особенностью аксиального дифракционного распределения оптических систем с малым числом Френеля, в частности, миллиметрового и субмиллиметрового диапазонов является его асимметрия. Из (З) следует, что слева от главного дифракционного максимума распределение - сжато, а справа - растянуто. Именно этот при-- знак, характеризующий форму дифр.ак- ционного распределения и был положен в основу способа измерения числа Френеля оптической систеъы и qooT- ветствующих геометрооптических да- раметров а и R.
Безразмерный числовой параметр характеризует форму распределения интенсивности в главном аксиальном дифракционном порядке, в частности его асимметрию (скошенность):
Z, +Z.,
sr-sT- /., -Л-
(А)
(3)
Z, J Z.,Z-, ,
(5)
51427196
г|це Z и Zl, - координаты первых мийиD q +p .
мумов дифракционного распределения в облает тях Z- О и Z О в системе координат, преобразованной относительно исходной путем сне- q т тх-ту 2 ir +9 ir(2-9S ).
D J(2) .4(1гЧз)0 и ПРИ любых .
щения начала отсчета в точку главного максиму- 10 ма интенсивности. Приняв во внимание (2) и (3), вы- ажение (5) можно перенисать в виде:
I2R
Анализируя последнее выражение, можно показать, что при
(тгЧз)
2R
В-5 .
(6)
() и q О при
,,i4 oS4iy :if .,.
„I2R 12R ,
-« - Р2
что представляет собой систему дгух
Воспользовавшись (4) и (6) и учитывая условие Я1толнения (2), можио перейти от области допусти1 1х значений асимметрии 8 к области допустиалгебраических уравнений 3-й степени 2° btx значений измеряемых чисел Фре- с двумя неизвестными R и N. В резуль- « Р ,25, qj-O тате простых преобразований можно по- при 2,205 3,25,
лучить
II
25
вЛ5|.:Ы , (Ч4)
и, осуществив подстановку, перейти к алгебраическому уравнению 3-й степени с одним неизвестным вида:
М +BN +eN+E 0, (7)
где А 1t«&;
В -2(1 -1-3);
,..
Используя известную методику замены переменной, уравнение (7) можно преобразовать к виду:
Искомые решения уравнения (8) определяются через вспомогательнь1е величины г и ср, причем знак г ±-J / pf должен совпадать со знаком коэффициента q,
При условии D л О и р О кубическое уравнение (8) имеет три действи- 30 тельных решения вида:
35
у, -2г cos(); y 2rcos(|- ); yj 2rcos( -fp.
(9)
где costf |з
y43py-i-2q 0,
(8)
D
где --T ;
2q
2B:
BC
27F 3F A
„ 3AC-B 3p -5j,- .
После необходимьге подстановок можо записать:
2()
;
4(43)
8()
iL
Число действительных решений урав- нения (8) зависит от знака дискриминанта D и коэффициентов р и q.
.
тх-ту 2 ir
q т тх-ту 2 ir +9 ir(2-9S )+547
D J(2) .4(1гЧз)0 и ПРИ любых .
10
Анализируя последнее выражение, можно показать, что при
(тгЧз)
() и q О при
,,i4 oS4iy :if .,.
2° btx значений измеряемых чисел Фре- « Р ,25, qj-O при 2,205 3,25,
25
Искомые решения уравнения (8) определяются через вспомогательнь1е величины г и ср, причем знак г ±-J / pf должен совпадать со знаком коэффициента q,
При условии D л О и р О кубическое уравнение (8) имеет три действи- 30 тельных решения вида:
у, -2г cos(); y 2rcos(|- ); yj 2rcos( -fp.
(9)
где costf |з
40 Для случая ( 0,735, N 3,25), осуществив подстановку в (9), можно перейти к соответствующим решениям исходного уравнения (7):
N
- оч.
f Ч. Л .
- J
Н тЧ -2-4 - 1 ( «
,,-a.os(-il.
Г, (37)8 Т где tf, arccos 1-
Аналогично для (0,735 ;& 1,
2, 3,25)
i 2(ЧгЧз) Г. 2 - -ЗтгТ L
cos
f л.
8
71427196
1 2( + Г.Г оЛ / ,писать в виде:
,..1 к2созЦ-))2(7ЧЗ)Г ,7 ..Л
.2( 1гЧз)Г, с,(-3
где
(fj arccos «Т-arccos
(3 2ТТ
( (
..,. NHgl).2co.-.).
Г. (37)S« 1
.
с учетом этого (П) можно пере N;EN; - 3w--f- ° --5 р
N; cos(| -f 5) при ,735; 4 cos(fl - ) при 0..
Следовательно: N N; ,2 cos() при
I-«
arccos
r, (3ir)Vl
L 2rf+3 JTOeCp- x -x-v.. L Srf+3 J
Из анализа полученных решений следует, что единствениым физически обоснованным решением является
N.-i|-Jjl| l+2 cos()l при .(13)
Второе решение при любом 5 в указанном интервале дает значение числа Френеля меньше нуля, что противоречит определению N, так кгис N
. Третье и четвертое решения
ri
при любых в в указанном интервале изменения дают NC 2, что противоречит определению 8 по (4), поскольку при отсутствует первый положительный минимум.
Приведем результаты применения способа измерения числа Френеля и геометрооптических параметров радиообъектива, вьтолненного в виде плоско-выпуклой линзы, изготовленной из оргстекла и имеющей следующие конструктивно-габаритные характеристики:
Радиус выходного
зрачка ЕК, мм Радиус сферической поверхности г мм
Фокусное расстояние f, мм Расстояние от вьг- ходного зрачка до параксиального
8
NHgl).2co.-.).
Следовательно: N N; ,2 cos() при
I-«
изображения точечного источника R, мм (12±1,4)-10 (с учетом того, что показатель преломления оргстекла ,9 мм ра- вен ,59±0,07);
Число Френеля такой микроволновой системы, определяемое по средним выборочным значениям а, RI-, X, равно , а относительная погрешность 8„ П%.
tta фиг. 2 представлено экспериментальное дифракционное распределение интенсивности вдоль оптической оси радиообъектива. Выборочный средний размер главного дифракционного порядка, полученный на основе прямых измерений, мм, а координаты первых минимумов Z,(l25iO,5) мм; Z, (95± 0,5) мм, что соответствует асимметрии S (О, 136±0, 05) .
Согласно формуле (13) число френеля ,2±0,7, а относительная .щ
грешность измерений ,
При использовании данного способа можно также определить геометроопти- ческие параметры системы а и R:
(14)
В данном случае выборочные средние значения указанных параметров равны мм, мм.
Контрольные измерения числа Френеля, выполненные по способу-прототипу дают следующие результаты: по размерам главного и первого положительного дифракционных порядков (Ъ Ц L ,6t1,4, 7%; размерам двух боковых дифракционных порядков (JL., к L) ,5il ,8,к 9%; по размерам главного и первого отрицательного дифракционных порядков (L и k,) .412;5„ 11%.
Результаты свидетельствуют о хорошем согласовании измеренных значе- 15 НИИ числа Френеля и геометрооптичес- 1|их параметров а и R с величинами, Определенными на основе контрольных измерений. При этом относительная Погрешность измерений по предлагаемо- 20 му способу в 2-3 раза меньше, чем по способу-прототипу.
5 0
Ф
0
ормула изобретения
Способ определения числа Френеля оптической .системы преимущественно в миллиметровом и субмиллиметровом диапазонах, включающий операции освещения точечным источником исследуемого объектива, регистрации распределения энергии в дифракционной картине вдоль оптической оси и определение числа Френеля N расчетным путем, о т- лич ающий ся тем, что, с целью повьтения точности и упрощения процесса измерений, определяют координаты первых минимумов Z, и z., главного дафракционного порядка,
I -. z;+z:, ,
личину его асимметрии и -,-;;г-
л, -Л-,
вычисляют N по формуле
не, а(,)
где Ч arccos
(37)8 2Tf +3T
11 /3
W 12
/«
J
Фие.1
г Ч
LO
71 1
Фиг.г
Выходной Зрачок
Зотн,
Фиг.з
| Труды ЛИТМО | |||
| - Л., 1978, с | |||
| Скоропечатный станок для печатания со стеклянных пластинок | 1922 |
|
SU35A1 |
| Способ определения числа Френеля оптической системы (его варианты) | 1984 |
|
SU1224644A1 |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
Авторы
Даты
1988-09-30—Публикация
1986-12-12—Подача