;л
ч
00




| название | год | авторы | номер документа |
|---|---|---|---|
| Многофункциональный логический модуль | 1985 |
|
SU1259243A1 |
| Многофункциональный модуль | 1983 |
|
SU1180877A1 |
| Многофункциональный логический модуль | 1982 |
|
SU1149244A1 |
| Устройство для полиномиального разложения симметрических булевых функций | 1988 |
|
SU1559338A1 |
| Универсальный логический модуль | 1984 |
|
SU1218375A1 |
| Устройство для полиномиального разложения логических функций | 1988 |
|
SU1550507A1 |
| Многофункциональный логический модуль | 1985 |
|
SU1247858A1 |
| Преобразователь формы представления логических функций | 1987 |
|
SU1441381A1 |
| МНОГОФУНКЦИОНАЛЬНЫЙ МОДУЛЬ | 2007 |
|
RU2348976C2 |
| Устройство для преобразования булевых функций | 1988 |
|
SU1532946A1 |
Изобретение относи ся к области в|)1числительной техники и может быть использовано при построении устройств обработки информации. Целью изобрете- ния является расширение функциональных возможностей многофункционального модуля заключакицееся в реализации функций К-значной логики от произвольного числа п переменных. Многофункциональный модуль содержит блоки элементов И 1,-1 (п+1)-входовой сумматор 2, логический блок 3, реализующий предикат. На информационные входы модуля подаются входные переменные, на настроечные входы - сигналы .настройки. На выходе многофункционального модуля реализуются К-значные логические функции. 2 ил. 7 табл.
muz.l
Изобретение относится к вычислительной технике и может быть использовано при построении устройств обработки информации.
Цель изобретения - расширение функциональных возможностей путем реализации К-значных логических функций от произвольного числа п переменНЬПС
Для достижения поставленной цели принципиальное значение имеет метод представления функций К-значной логи ки.
Пусть RK 0,1,2,...,К-1} - мно- |Жество, состоящее из К элементов. Определим на этом множестве две бинар- ные операции аОЬ и а@Ь (а,Ь 6 R ). Операцию а0Ь зададим таблицей Кэли (табл.1).
Эту жв операцию можно задать аналитически;
О, если или
a+b-1(inod(K-1)), если 1и .
(О
30
Назовем так заданную операцию аОЬ умножением. Тогда R, О - мкльтипликативная полугруппа, а подмножество к I 0 с операцией О образует циклическую группу R, 0 с образующим элементом 2еR, т.е. все элементы множества Rt можно записать в виде степеней элемента 2, При этом имеют место следующие соотношения :
a,если ,
b,если ,
a0fii, если , (4)
. , ,..., где 2 О... 02.
а(9Ь и , причем ,, аО(2Орк-(.1 ), если , и а о , причем i s,
где а - обратный элемент к элементу относительно операции умножения, т.е. 1.
Так, в случае квазиполя порядка (2) операции умножения О и сложения © можно задать соответственно табл. 3 и 4.
40
45
1 раз
Операцию а®Ь, которую назовем сложением, определим так, чтобы выполнялись аксиомы:
,jj
.
,5 0
5
Множество R с определенными на нем таким образом операциями умножения О и сложения 0 называют квазиполем и обозначают символом R, о, ©.
Операция a®b, удовлетворяющая аксиомам (3), полностью задается значениями fJ;(,1,..., г обозначение целой части числа г)о Элементы ;(,s) называют определяющими элементами квазиполя RK,O,@ Наборы определяющих элементов р, ,/} , ..., 5 строятся неоднозначно. Один из способов опстроения набора определяющих элементов состоит в следующем для К -четного , для К нечетного
/i,d+t+n где , , а значения /Ji , ,..., равны соответственно: d+1,2,d-f2,3,d+3,4,...,t,d+t, t+1, если S - четное, и d+l,2,d+2,3, d+3,4,...,t,d+t, если s - нечетное. В табл.2 приведены определяющие элементы квазиполей при К 20.
Если известны определяющие элементы ; квазиполя iRy;, О,® ,, то операция а csb задается следующим образом:
a,если ,
b,если ,
a0fii, если , (4)
а(9Ь и , причем ,, аО(2Орк-(.1 ), если , и а о , причем i s,
Зададим далее на множестве R некоторый предикат P:Ry- R|. Предположим, что функция К-значной логики f(х,,х,...,х) представима в параметрическом виде над квазиполем RH,G,®, если существует набор (Wo,W,...,W), где W jeR(j-0,n),
такой, что
г (,х,х,.. о ,Х| P(Wo©W,...,). (5)
3145
Так, в случае квазиполя восьмого порядка (, операции умножения О и сложения © заданы соответственно табл.3 и 4), если предикат Р задать табл.5, то представление в виде (5) допускают все булевые функции двух переменных, а также 213 булевых функций трех переменных из 256.
Значения W , W,, W-j, при которых из P(WO® W,e x,@W2© хр получаются все булевы функции двух переменных, приведены в табл.6.
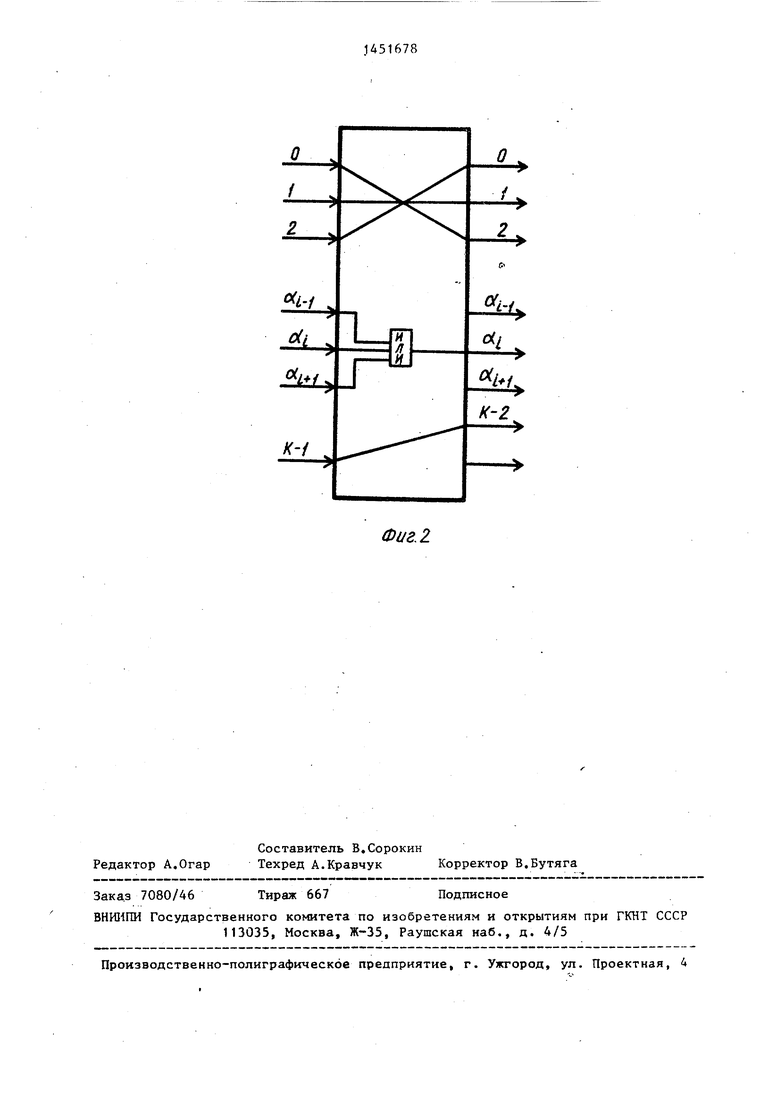
На фиг.1 представлена структурная схема многофункционального модуля, на фиг.2 - пример функциональной схемы логического блока, реализующего
предикат./,
Многофункциональный модуль .фиг.и содержит блоки элементов И 1.1-1.П, (п+1)-входоврй сумматор 2, логический блок 3, реализующий предикат, информационные входы 4.1-4.П модуля, группу настроечных входов 5.1-5.П модуля, настроечный вход 6 модуля и выход 7 модуля.
Многофункциональный модуль работает следующим образом.
Сигналы, представляющие входные переменные х,,...,х,...,х, подаются на соответствующие информационные входы модуля. На группу настроечных входов 5.1-5.п подаются сигналы W „... .W; .... ,W соответственно, на управляющий вход 6 - сигнал W. В результате на выходах блоков И 1.1 i.n формируются сигналы, представляющие результаты умножения переменных х.,...,х.,...,х „на W,,...,W,,...,Wrt соответственно. Сигналы, представляющие результат сложения W с произведениями W,.0x (,n), с выходов суммируницего блока 2 подаются на входы логического блока 3, реализую- щего предикат. ,
678
Одноместный предикат Р реализуется в результате перекодирования значенМ сигналов, представляющих область его определения. Перекодировка выполня ется в соответствии с соотношением
РгКк- К
к
Пусть, например, предикат Р задается соответствием, представленным В табл.7.
Функциональная схема устройства, реализующего такой предикат Р, показана на фиг.2.
При пространственном представлении перекодировка значений сигналов может быть реализована в результате перенумерации щин и последующего подключения к соответствующим входным шинам преобразователя пространственных сигналов в фазоимпульсные.
Формула
изобретения
Многофункциональный модуль, содержащий п блоков элементов И, причем i-й (,п) информационный вход модуля соединен с первыми входами элементов И i-ro блока, вторые входы „ которых соединены с i-м настроечным входом группы модуля, отличающийся тем, что, с целью расширения функциональных возможностей за счет реализации К-значных логических функций от произвольного числа п переменных, в него введены (п+1)-вхо- довой сумматор и логический блок, реализующий предикат, причем выходы элементов И всех блоков соединены с входами i-ro слагаемого (п-И)-входо- вого сумматора, вход (i+1)-го слагаемого которого соединен с настроечным входом модуля, выход (п+1)-вхо- дового сумматора соединен с входом логического блока, реализующего предикат, выход которого является выходом модуля.
5
0
45
О О
К-2 К-1
К-1 1
2 3
К-4 К-3
К-3 К-2
Таблица2
:11ГЛ1 Л1Г111-ШЯ1
&
о
2 3
4 5 6
7
Таблица
1 5
2 6 3 О
ТаблицаЗ
5 6 7
«Я Ч- Г
о 1 о
I
P(W)
л
кч
Редактор А.Огар
Составитель В.Сорокин
Техред А.КравчукКорректор В.Бутяга
Заказ 7080/46
Тираж 667
ВНИИПИ Государственного кo итeтa по изобретениям и открытиям при ГКНТ СССР 113035, Москва, Ж-35, Раушская наб., д. 4/5
Фиг.
Подписное
| Универсальный логический модуль | 1985 |
|
SU1282113A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Многофункциональный модуль | 1983 |
|
SU1180877A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1989-01-15—Публикация
1987-06-02—Подача