V
(Л



| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для распознавания на линейность булевых функций | 1990 |
|
SU1756879A1 |
| Устройство для преобразования булевых функций | 1988 |
|
SU1532946A1 |
| Модуль для логических преобразований булевых функций | 1989 |
|
SU1667050A1 |
| Устройство для вычисления булевых производных | 1988 |
|
SU1518825A2 |
| Устройство для вычисления булевых дифференциалов | 1989 |
|
SU1777132A1 |
| Преобразователь формы представления логических функций | 1987 |
|
SU1474671A1 |
| Устройство для вычисления импликант | 1989 |
|
SU1686460A1 |
| Устройство для решения булевых дифференциальных уравнений | 1989 |
|
SU1661791A1 |
| Логический вычислитель в системе остаточных классов | 2016 |
|
RU2637488C1 |
| Магнитооптическое устройство для реализации дискретного преобразования Фурье | 1990 |
|
SU1795472A1 |
Изобретение относится к цифровой вычислительной технике и может быть использовано для аппаратной поддержки вычислений в комплексах автоматизированного проектирования дискретных устройств, обработки изображений, сжатия данных, в системах синтеза топологии БИС и СБИС. Целью изобретения является расширение функциональных возможностей за счет распознавания на линейность булевых функций, заданных в обобщенной арифметической полиномиальной форме. Указанная цель достигается тем, что устройство содержит коммутатор 1, блок 2 регистров, вычислительный блок 3 и блок 4 управления. 6 ил., 1 табл.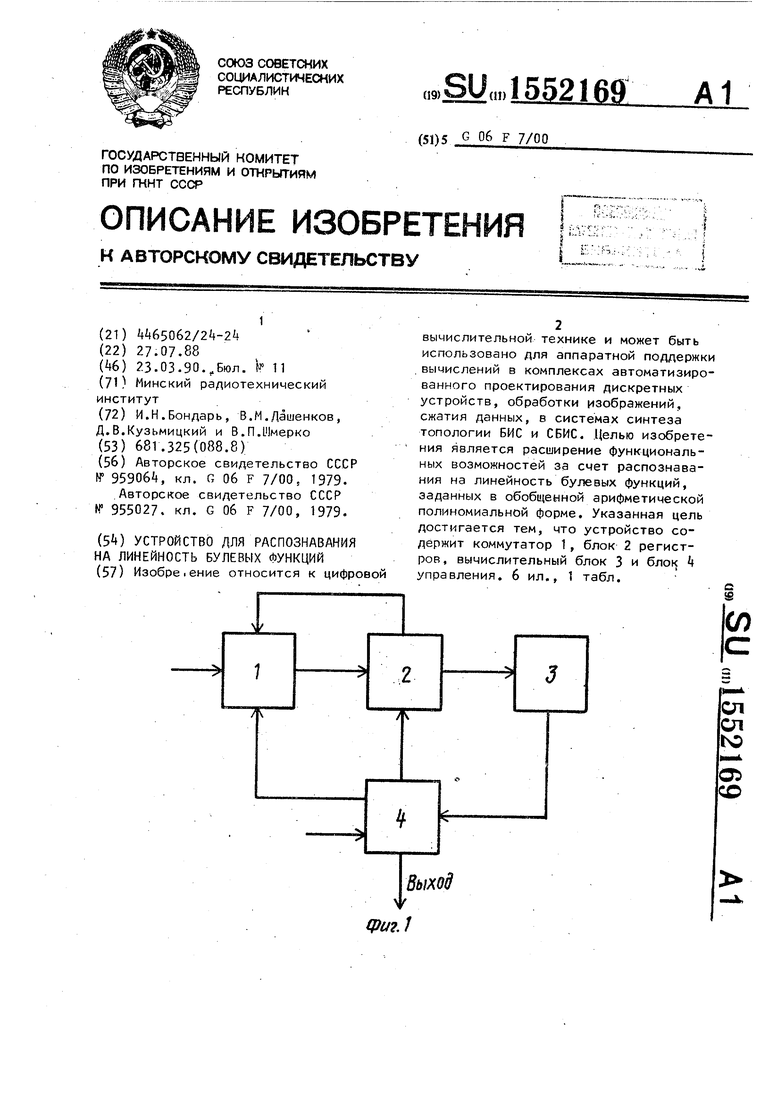
I
1
сд
ел
О5
со
Выход
фи,1
Изобретение относится к цифровой вычислительной технике и может быть ис- пйльзовано для аппаратной поддержке вычислений в комплексах автоматизирован наго проектирования дискретных устройств, обработки изображений, сжатия данных, в системах синтеза топологии БИС и СБИС.
Целью изобретения является расши- функциональных врзможностей за счет распознавания на линейность булевых функций, заданных в обобщенной арифметической полиномиальной форме.
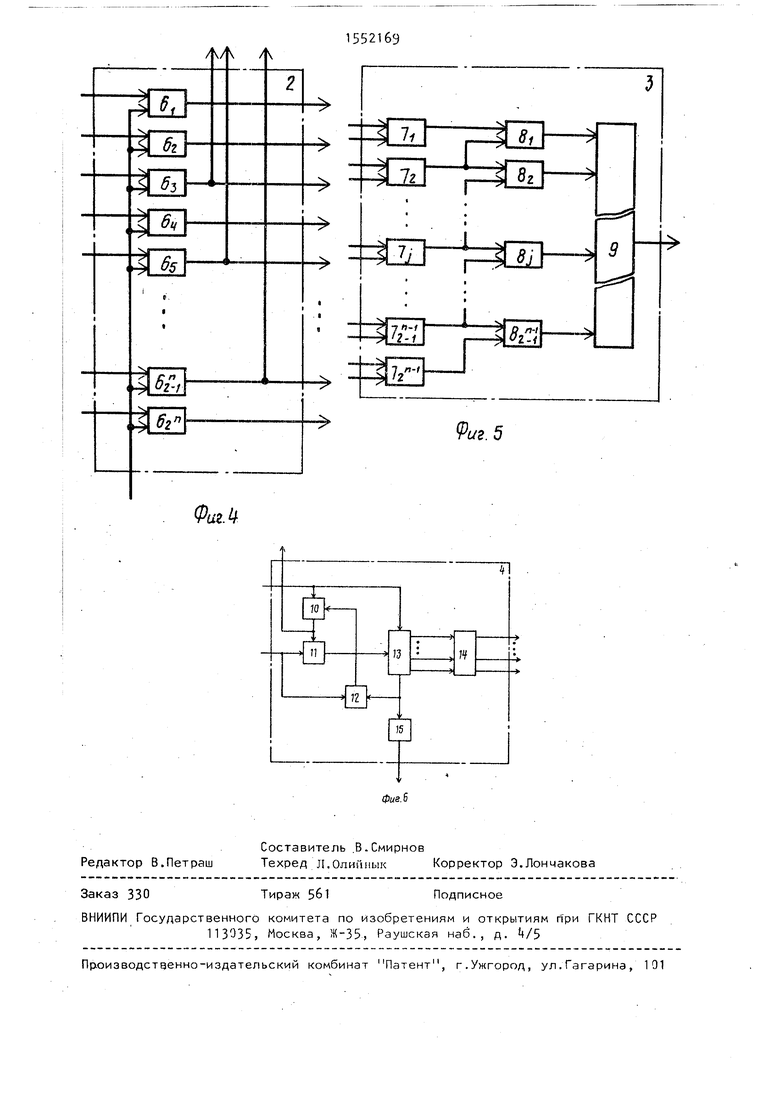
На фиг. 1 представлена схема устройства-, на фиг. 2 - схема коммутатора; на фиг. 3 функциональная схема узла мультиплексоров; на фиг. h - схема блока регистров; на фиг. 5 схема вычислительного блока; на фиг. 6 - схема блока управления.
Устройство содержит коммутатор 1, блок 2 регистров, вычислительный блок 3 и блок k управления. Коммута- тор 1 содержит - .1 узлов 5 мультиплексоров, где п - число переменных булевых функций. Блок 2 регистров содержит 2П регистров 6 Вычислительный бл;ок 3 содержит 2П вычитателей 7 2 - 1 элементов 8 сравнения и элемент И 9. Блок А управления содержит генератор 10 тактовых импуль- сбв, элемент И 11. элемент И-НЕ 12, сметчик 13- дешифратор 1 и триггер
19,
Арифметическая полиномиальная фор- м;| булевой функции f(x) имеет следующий вид:
Р(х) Р0 + Pfxn + p2x,,t +
+ . . -fPnn.j X 4 ХП
2«-i.
чг- i Ч п-1 и/1
И pixi Х Хч 0
где p;6z (i 0,2 - 1),Z - множество целых чисел таких, что значение Р(Х) ,l на любом наборе переменных,
X1 в Y. ; - Ai
Я° & 1
Л; I 1. Х ...
1n-. in
n-разрядный двоичный
код представления пара метра i.
Арифметическая полиномиальная форма Р(Х) булевой функции f(x) опреде
ляется вектором коэффициентов Р
рв. Р,, ... Рг«-1- OT, который является результатом выполнения конъюнктивного преобразования над вектором значений Х. х(0 х ... х J булевой функции f(x).
Р KtnXi(
(2)
где - матрица конъюнктивного преобразования размерности 2П х .п. формируемая по правилу
К0„ К„, ® KeB.t ,
(3)
где ® - символ кронекеровского произведения.
Обобщенная арифметическая полиномиальная форма задает уже систему (кортеж) булевых функций, упорядоченную пространственно. Эта система записывается в виде
Јпь.(х)) ...f0,
Если j-ю функцию кортежа (j 0,т-1) представить в виде арифметической полиномиальной формы Р; (х), затем умножить на весовой множитель 24 и полученные с весами полиномы сложить, то результатом является обобщенная арифметическая полиномиальная форма D(x), где
m-i
D(x) JT 2J Р. (х)
2я-1
Г°
d- х ;х
п-г Х„-,Хп
Обобщенная арифметическая полиномиальная форма системы булевых функций D(x) однозначно представляется вектором коэффициентов D Јde, d t, ... , d 2.n, r.
Линейная обобщенная арифметическая полиномиальная форма системы булевых функций fj(x) (j 0,,m-1) имеет следующий вид:
LD(x) 10 + 1,хп + 14хпн +
П
+ ... + - 10 + .(5)
1™1
51552169
з (5) видно, что обобщенная арифнепо эл це не ли ра ке
метическая полиномиальная форма является линейной, если в ее состав входят только слагаемые, определяемые лишь одной булевой переменной х ; (i 1,п).
Таким образом, если коэффициенты обобщенной арифметической полиномиальной формы П(х) удовлетворяют условию
СО
d ; О для i jЈ 2 , СО 0,п-1 , i -0,,
то данная обобщенная арифметическая полиномиальная форма системы булевых функций является линейной.
Линейная обобщенная арифметическая полиномиальная форма системы булевых функций однозначно определяется вектором коэффициентов LD 10, 1,, ..., 1„3Т Характерным свойством является то, что этот вектор коэффициентов содержит всего п + 1 элемент,- тогда как вектор коэффициентов нелиx ol - xw х(г1 - х™ - х(-хЫ х(0) - xul - х(41 - х(б1
x(n
- Л
ХЮ1 . Х(2П х(
Вычислительный блок 3 работает следующим образом. Элементы вектора значений Хл (х(о1, , ..., поступают ни входы вычитателей 7. в которых формируются значения разностей поступивших элементов х 2 - х г . С выходов вычцтателей 7i :
fi -И (f2 )
значения разностей хы - х передаются на входы элементов 8 и 8j сравнения, с выхода которых си|- нал равенства операндов на входах (высокий логический уровень) поступает на вход элемента И 9, на выходе которого формируется высокий логический уровень в случае высоких логических уровней на всех его входах. Дешифратор 14 предназначен для формирования сигналов на своих выходах в соответствии с таблицей.
Блок k управления работает следующим образом. В момент времени t, высокий логический уровень напряжения поступает на вход запуска гене
-нейной обобщенной арифметической полиномиальной формы содержит 2 элементов. Это свойство определяет целесообразность использования линейной обобщенной арифметической полиномиальной формы, позволяющей сократить объем вычислений при обработке и объем памяти при хранении век10 торов коэффициентов. Таким образом, возникает необходимость распознавания на линейность обобщенных арифметических полиномиальных форм, заданных своими векторами значений Х,.
15 Для обобщенной арифметической полиномиальной формы системы булевых функций между вектором значений Х и вектором коэффициентов D существует взаимно однозначное соответствие,
20 onpeделяемое выражением
о к2„.хв.
(7)
Из (7) следует, что в общем случае 25 условие линейности обобщенной арифметической полиномиальной формы имеет вид
(-хЫ
()
x( . x( j
- ЛА
- х
()
(8)
ратора 10 тактовых импульсов, а также на первый вход счетчика 13, в который записывается число 2 - п, код этого числа с выходов счетчика
13 поступает на входы дешифратора 14,на выходах которого формируются низкие логические уровни напряжения в соответствии с таблицей.
В момент времени tz на выходе генератора 10 формируется тактовый импульс , поступающий через элемент И 11 на второй вход счетчика 13.Счетчик 13 переходит в состояние 2 - п + + 1, код с выходов счетчика 13 поступает на входы дешифратора 14, на вы
ходах которого формируются сигналы в соответствии с таблицей.
В моменты времени t4 и ts работа блока 4 управления происходит аналогично работе в момент времени tj,, только счетчик 13 переходит в состояния 2k-n + 2n2k-n + 3 соответственно.
В момент времени tg счетчик 13 при оступлении на его второй вход тактопуле ка в ме Со 2
вого импульса переходит из состояния 2k - 1 в состояние 0, и с его выхода сигнал переполнения поступает на Ьходы элемента И-НЕ 12 и триггера 15-. который переходит из нулевого в единичное состояние. С выхода элемента И-НЕ 12 сигнал фронта напряжения с Низкого логического уровня на высокий Поступает на вход останова генератора 10 тактовых импульсов.
Рассмотрим работу устройства для случая п 4. Элементы вектора знапульс с второго выхода блока 4 управления поступает на вход записи блока 2 регистров и синхронизирует запись в его регистры 6г- 64 значений элементов х(41 , хсгл , х ( вектора хо Содержимое остальных регистров блока 2 регистров остается без изменения.
Если выполняется х(с - х х « 0 „ («л
15
, то на выходе вычислительного блока 3 сохраняется высокий логический уровень напряжения,, Счетчик 13 переходит из состояния 110 в состояние 111.
посту- 1Э В момент времени te тактовый импульс поступает на счетный вход счетчика 13; который при этом переходит из состояния 111 в состояние 000 и формирует сигнал переполнения. Сигнал переполнения поступает на вход триггера 15 и переводит его в единичное состояние, а также поступает на вход элемента И-НЕ 12 и далее
чений Хэ х (0. х«5) пают на информационные входы первой Группы устройства. После поступления На вход режима блока А управления высокого логического уровня (момент времени ц) в счетчик 13 записывается число, равное 2 , ему соотствуествует код 100, следовательно, на первом выходе блока Ц управления формируются нулевые сигна- 25 на 8Х°Д останова генератора 10 тзк20
лы, которые передаются на управляющий вход коммутатора 1 .
Выработанный генератором 10 тактовый импульс (момент времени t) поступает на вход записи регистров 6 и синхронизирует запись в регистры 6 элементов вектора значений Х-р, поступающих с выхода коммутатора 1 . Под действием этого тактового импульса счетчик 13 переходит из состояния 100 в состояние 101. Если выполняется х - хм ) 30
35
XU1 x(7l XW
X W Х(4)
х( Х00)
) (К)
)
- х) - х UV|
то на выходе вычислительного блока
3 остается высокий логический уровень,
В момент времени ц тактовый импульс с второго выхода блока 4 управления передается на вход записи регистров 6 и синхронизирует запись в них элементов вектора значений X,
40
45
Д6)
. ((О)
,х
Ог) v(
х, ), Эти значения записываются в регистры 6р (р 2,8), в остальные регистры блока 2 регистров записывается та же
товых импульсов.
Таким образом, наличие единичного состояния триггера 15 при остановленном генераторе 10 тактовых импульсов свидетельствует о линейности распознаваемой обобщенной арифметической полиномиальной формы.
Если обобщенная арифметическая полиномиальная форма не является линейной, то на этапе распознавания (например, в момент времени t) не выполняется одно из равенств (7). При этом на выходе вычислительного блока 3 формируется низкий логический уровень напряжения, этот сигнал поступает на вход режима блока 4 управления и далее на вход элемента И-НЕ 12, с выхода которого высокий логический уровень напряжения передается на вход останова генератора 10, Таким образом, наличие нулевого состояния триггера 15 при остановленном генераторе 10 тактовых импульсов свидетельствует о непринадлежности распознаваемой обобщенной
информация, которая была в них записа-50 арифметической полиномиальной формы
На выходе
на в момент времени tz. вычислительного блока 3 остается высокий логический уровень напряжения в случае выполнения х - х
х(40 х(6) х(й) х (W) х Н О - х 4 . Под действием этого же тактового импульса счетчик 13 переходит из состояния 101 в состояние 110.
В момент времени t& тактовый им
пульс с второго выхода блока 4 управления поступает на вход записи блока 2 регистров и синхронизирует запись в его регистры 6г- 64 значений элементов х(41 , хсгл , х ( вектора хо Содержимое остальных регистров блока 2 регистров остается без изменения.
Если выполняется х(с - х х 0 „ («л
, то на выходе вычислительного блока 3 сохраняется высокий логический уровень напряжения,, Счетчик 13 переходит из состояния 110 в состояние 111.
0
5
0
5
товых импульсов.
Таким образом, наличие единичного состояния триггера 15 при остановленном генераторе 10 тактовых импульсов свидетельствует о линейности распознаваемой обобщенной арифметической полиномиальной формы.
Если обобщенная арифметическая полиномиальная форма не является линейной, то на этапе распознавания (например, в момент времени t) не выполняется одно из равенств (7). При этом на выходе вычислительного блока 3 формируется низкий логический уровень напряжения, этот сигнал поступает на вход режима блока 4 управления и далее на вход элемента И-НЕ 12, с выхода которого высокий логический уровень напряжения передается на вход останова генератора 10, Таким образом, наличие нулевого состояния триггера 15 при остановленном генераторе 10 тактовых импульсов свидетельствует о непринадлежности распознаваемой обобщенной
к классу линейных.
Формула изобретения
Устройство для распознавания на линейность булевых функций, содержа1 щее коммутатор, вычислительный блок и блок управления, отличающееся тем, что, с целью расширения функциональных возможностей за счет распознавания на линейность булевых функций, заданных в обобщен ной арифметической полиномиальной форме, оно содержит 2П регистров (где п - число переменных булевых функций), причем входы вектора значений обобщенного арифметического полинома устройства подключены соот ветственно к информационным входам первой группы коммутатора, выходы с первого по 2п-й которого подключены соответственно к информационным вхо
П м
n-l
дам регистров с первого по 2 -и, выходы регистров с первого по (2 -1)-й подключены соответственно к информационным входам второй группы
00000000 11111111 11111111
%tl
коммутатора и соответственно к информационным входам первой группы вычислительного блока, выходы регистров с 2п -го по 2п-й подключены соответственно к информационным входам второй группы вычислительного блока, выход которого подключен к входу режима блока управления, перIQ вый, второй и третий выходы которого подключены соответственно к управляющему входу коммутатора, к входам записи всех регистров и к выходу признака линейности распознаваемой обоб- 15 щенной арифметической полиномиальной формы устройства, вход запуска которого подключен к входу запуска блока управления.
. о . 1
. о
.Ъ
Редактор В.Петраш
Составитель В.Смирнов
Техред л.Олш шык Корректор Э.Лончакова
Заказ 330
Тираж 5б1
ВНИИПИ Государственного комитета по изобретениям и открытиям при ГКНТ СССР 113035, Москва, Ж-35, Раушская наб., д. /5
Производственно-издательский комбинат Патент, г.Ужгород, ул.Гагарина, 101
Подписное
| Устройство для вычисления симметричных булевых функций | 1980 |
|
SU959064A1 |
| Способ восстановления хромовой кислоты, в частности для получения хромовых квасцов | 1921 |
|
SU7A1 |
| Устройство для вычисления булевых функций | 1980 |
|
SU955027A1 |
| кл | |||
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1990-03-23—Публикация
1988-07-27—Подача