Предлагаемое устройство относится к вычислительной технике и может быть использовано для аппаратной реализации криптографических примитивов.
Известен арифметический вычислитель систем булевых функций [1], содержащий n входов подачи булевых переменных, коммутатор, 2k блоков памяти хранения групп коэффициентов, n-k+1 мультиплексоров выделения группы коэффициентов, многоместный сумматор, d выходов выдачи значений булевых функций, причем информационные входы коммутатора являются входами подачи булевых переменных устройства, а выходы с (k+1)-го по n-ый подключены к информационным входам каждого из 2k блоков памяти хранения коэффициентов, выходы которых подключены к информационным входам каждого из (n-k+1) мультиплексоров выбора группы коэффициентов, где i-ый выход j-го блока памяти подключен к j-му входу i-го мультиплексора (i=1, 2, …, n-k+1; j=1, 2, …, 2k), управляющие входы каждого из которых соединены с k первыми выходами коммутатора, а выходы подключены к многоместному сумматору, d мультиплексоров выделения информационного разряда, многоканальный мультиплексор, 2k блоков памяти хранения адресов информационных разрядов, управляющий вход подачи сигнала выбора булевых переменных разложения, который является управляющим входом коммутатора, а управляющий вход подачи сигнала выбора реализуемой булевой функции устройства является управляющим входом каждого из 2k блоков памяти хранения коэффициентов и каждого из 2k блоков памяти хранения адресов информационных разрядов, выходы каждого из которых подключены к информационным входам многоканального мультиплексора, управляющие входы которого соединены с первыми k выходами коммутатора, а выходы с 1-го по d-ый подключены к адресным входам d мультиплексоров выделения информационного разряда соответственно, информационные входы каждого из которых соединены с выходами многоместного сумматора, а выходы являются выходами выдачи значений булевых функций устройства.
Недостатком известного устройства являются большие объемы оборудования.
Наиболее близким по сущности технического решения к заявленному устройству является модулярный полиномиальный вычислитель систем булевых функций [2], содержащий коммутатор, информационные входы которого являются n входами подачи булевых переменных устройства, управляющие входы которого подключены к управляющему входу устройства подачи значения количества переменных разложения, 2k блоков памяти хранения значений коэффициентов полиномов разложения, управляющие входы которых подключены к управляющему входу устройства подачи значений коэффициентов, информационные выходы которых подключены к информационным входам многоканального мультиплексора выделения группы коэффициентов, управляющие входы которого подключены к k первым выходам коммутатора, 2n-k блоков памяти хранения значений вычетов возведения переменной в i-тую степень, где i=0, 1, …, 2n-k-1 по модулю Р, управляющие входы которых подключены к управляющему входу устройства подачи значений вычетов возведения переменной в i-тую степень по модулю Р, информационные выходы которых подключены к информационным входам многоканального мультиплексора выделения группы вычетов, управляющие входы которого подключены к n-k вторым информационным выходам коммутатора, 2n-k умножителей по модулю Р, где входы j-го умножителя по модулю Р подключены к j-ым информационным выходам многоканального мультиплексора выделения группы коэффициентов и многоканального мультиплексора выделения группы вычетов, где j=1, 2, …, 2n-k, выходы которых подключены к входам сумматора по модулю Р, d выходов которого являются d выходами устройства выдачи значений булевых функций.
Недостатком данного устройства являются также большие объемы оборудования.
Цель изобретения - уменьшение объемов оборудования устройства.
Поставленная цель достигается тем, что в логический вычислитель в системе остаточных классов, содержащий коммутатор, информационные входы которого с 1-го по n-ый подключены соответственно к n входам подачи значений булевых переменных, являющимся входами устройства, управляющий вход которого подключен к входу подачи значения количества переменных разложения, являющемуся входом устройства; 2k блоков памяти хранения значений коэффициентов, входы которых подключены к входу подачи значений коэффициентов полиномов разложения, являющемуся входом устройства, а 2n-k выходов каждого из блоков памяти хранения значений коэффициентов подключены соответственно к группам информационных входов многоканального мультиплексора, управляющий вход которого подключен к 1-му выходу коммутатора; двухвходовый многоразрядный умножитель по модулю, 2-ой информационный вход которого подключен к 2-му выходу коммутатора; d выходов выдачи значений булевых функций, являющихся выходами устройства, введены распределитель тактовых импульсов, 1-ый выход которого подключен к управляющему входу вычитающего счетчика, 2-ой выход которого подключен к управляющему входу двухвходового многоразрядного сумматора по модулю, 3-ий выход которого подключен к управляющему входу двухвходового многоразрядного умножителя по модулю; вход подачи значения начального заполнения счетчика, являющийся входом устройства, который подключен к входу вычитающего счетчика; мультиплексор, управляющие входы с 1-го по (n-k)-ый которого соответственно подключены к выходам вычитающего счетчика, информационные входы с 1-го по 2n-k-ый которого соответственно подключены к 2n-k выходам многоканального мультиплексора, а выход подключен к 2-му информационному входу двухвходового многоразрядного сумматора по модулю, при этом 1-ый вход двухвходового многоразрядного сумматора по модулю подключен к выходу двухвходового многоразрядного умножителя по модулю, а выход подключен к 1-му информационному входу двухвходового многоразрядного умножителя по модулю и информационному входу выходного регистра, при этом выходы с 1-го по d-ый выходного регистра подключены соответственно к d выходам выдачи значений булевых функций; многовходовый логический элемент ИЛИ-НЕ, (n-k) входов которого подключены соответственно к (n-k) выходам вычитающего счетчика, а выход подключен к управляющему входу выходного регистра.
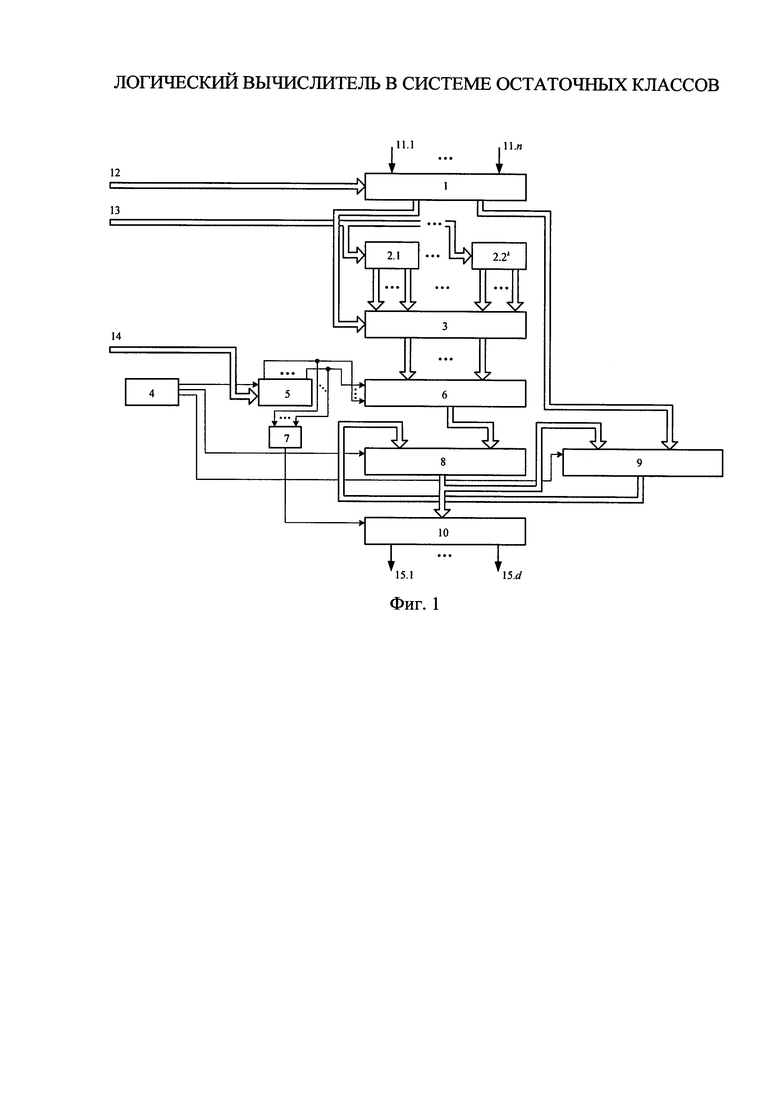
Структурная схема предлагаемого устройства представлена на фиг. 1, которое содержит коммутатор 1, блоки памяти хранения значений коэффициентов 2.1-2.2k, многоканальный мультиплексор 3, распределитель тактовых импульсов 4, вычитающий счетчик 5, мультиплексор 6, многовходовый логический элемент ИЛИ-НЕ 7, двухвходовый многоразрядный сумматор по модулю 8, двухвходовый многоразрядный умножитель по модулю 9, выходной регистр 10, входы подачи значений булевых переменных 11.1-11.n, вход подачи значения количества переменных разложения 12, вход подачи значений коэффициентов полиномов разложения 13, вход подачи значения начального заполнения счетчика 14, выходы выдачи значений булевых функций 15.1-15.d.
В статическом виде элементы предлагаемого устройства взаимосвязаны следующим образом (фиг. 1): входы подачи значений булевых переменных 11.1-11.n с 1-го по n-ый подключены соответственно ко входам с 1-го по n-ый коммутатора 1, управляющий вход которого подключен к входу подачи значения количества переменных разложения 12, при этом 1-ый выход коммутатора 1 подключен к управляющему входу многоканального мультиплексора 3, а 2-ой выход подключен ко 2-му информационному входу двухвходового многоразрядного умножителя по модулю 9; вход подачи значений коэффициентов полиномов разложения 13 подключен ко входам блоков памяти хранения значений коэффициентов 2.1-2.2k, при этом 2n-k выходов каждого блока памяти хранения значений коэффициентов 2.1-2.2k подключены к соответствующим группам информационных входов многоканального мультиплексора 3 (выходы с 1-го по 2n-k-ый i-го блока памяти хранения значений коэффициентов 2.i подключены к входам с 1-го по 2n-k i-ой группы информационных входов многоканального мультиплексора 3, i=1, 2, …, 2k); вход подачи значения начального заполнения счетчика 14 подключен ко входу вычитающего счетчика 5, при этом управляющий вход вычитающего счетчика 5 подключен к 1-му выходу распределителя тактовых импульсов 4, а выходы с 1-го по (n-k)-ый подключены к управляющим входам с 1-го по (n-k)-ый мультиплексора 6 и подключены к входам с 1-го по (n-k)-ый многовходового логического элемента ИЛИ-НЕ 7; информационные входы с 1-го по 2n-k-ый мультиплексора 6 подключены соответственно к выходам с 1-го по 2n-k-ый многоканального мультиплексора 3, а выход мультиплексора 6 подключен к 2-му информационному входу двухвходового многоразрядного сумматора по модулю 8, 1-ый информационный вход которого подключен к выходу двухвходового многоразрядного умножителя по модулю 9, при этом управляющий вход двухвходового многоразрядного сумматора по модулю 8 подключен к 2-му выходу распределителя тактовых импульсов 4, а выход подключен к 1-му информационному входу двухвходового многоразрядного умножителя по модулю 9 и подключен к информационному входу выходного регистра 10; 3-ий выход распределителя тактовых импульсов 4 подключен к управляющему входу двухвходового многоразрядного умножителя по модулю 9; выход многовходового логического элемента ИЛИ-НЕ 7 подключен к управляющему входу выходного регистра 10, выходы которого с 1-го по d-ый подключены соответственно к выходам выдачи значений булевых функций 15.1-15.d.
Сущность функционирования прототипа [2] заключается в вычислении полиномиального представления системы булевых функций с применением разложения по булевым переменным, где для представления системы булевых функций (СБФ) ƒ1, …, ƒd интерполяционным полиномом интерпретируются значения наборов переменных СБФ и значения функций на этих наборах как записи чисел в двоичной системе счисления и затем в десятичной:
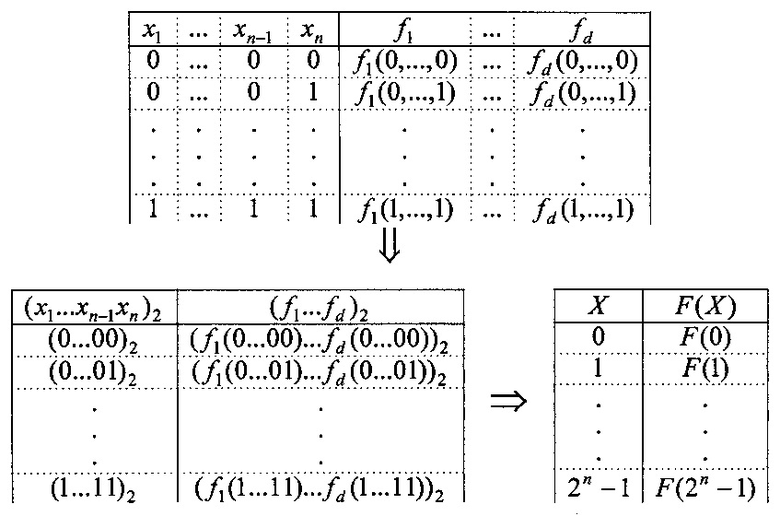
В результате данной интерпретации получается функция F(X), область значения и область определения которой {0, 1, …, s-1}, где s=2n.
Значения аргумента X являются равноудаленными узлами интерполирования, что обеспечивает возможность применения различных способов интерполяции к интерпретированной форме записи СБФ.
Воспользуемся методом интерполяции Лагранжа для представления F(X) степенным полиномом:
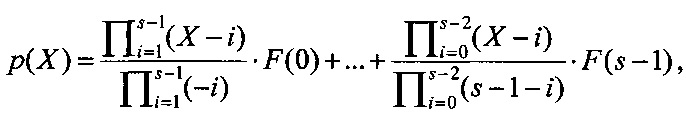
или
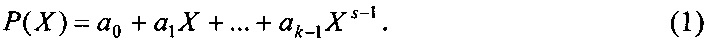
а i - коэффициенты полинома, (i=0, 1, …, s-1), s=2n.
Рассмотрим представление СБФ в модулярной интерполяционной полиномиальной форме представления системы булевых функций.
Так как
a -1≡aϕ(P)-1(modP),
где М - простое число, ϕ(М) - функция Эйлера, то интерполяционный полином (1) примет вид:
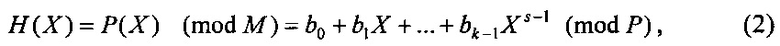
где bi≡ai (mod Р), i=0, 1, …, s-1, Р - простое число, Р>s.
Достоинством модулярной интерполяционной полиномиальной формы представления СБФ является значительное уменьшение коэффициентов полинома.
Общий вид разложения модулярной интерполяционной формы представления СБФ по одной булевой переменной примет вид:

где
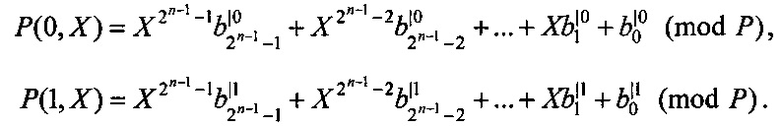
Общий вид разложения модулярной интерполяционной формы представления СБФ по k булевым переменным примет вид:
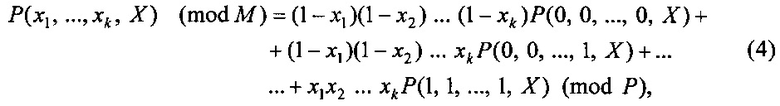
где
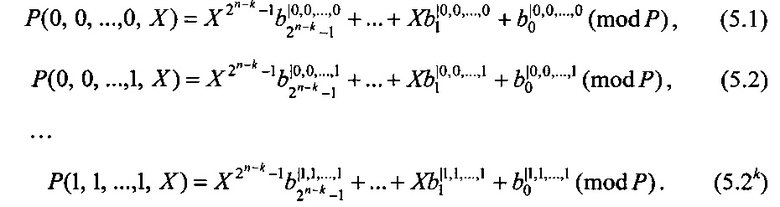
Вычисление представления СБФ (5.1-5.2k) с применением разложения по k булевым переменным требует значительных вычислительных ресурсов, что связано с выполнением большого количества многоразрядных операций сложения и умножения.
В отличие от прототипа в предложенном устройстве вычисление полиномов (5.1-5.2k) выполняется по схеме Горнера:
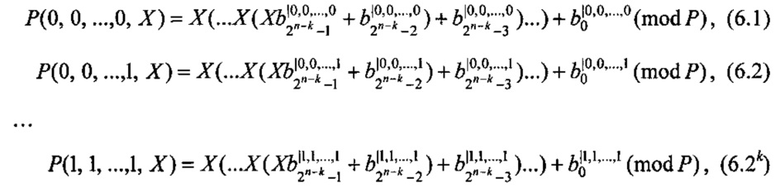
что позволяет сократить количество двухвходовых многоразрядных умножителей по модулю с 2n-k (в случае прототипа) до 1-го (в случае заявленного устройства) и заменить 2n-k входовый многоразрядный сумматор по модулю (в случае прототипа) на двухвходовый многоразрядный сумматор по модулю (в случае заявленного устройства).
Функционирование устройства осуществляется следующим образом: в момент времени, соответствующий началу работы, с входа подачи значения количества переменных разложения 12 на вход коммутатора 1 подается значение количества переменных разложения, также с входа подачи значений коэффициентов полиномов разложения 13 выполняется запись значений коэффициентов полиномов разложения (6.1-6.2k) в блоки памяти хранения значений коэффициентов 2.1-2.2k, где коэффициенты 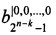 , …,
, …, 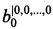 записываются в блок памяти хранения значений коэффициентов 2.1, и так далее, и коэффициенты
записываются в блок памяти хранения значений коэффициентов 2.1, и так далее, и коэффициенты 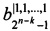 , …,
, …, 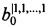 записываются в блок памяти хранения значений коэффициентов 2.2k, также со входа подачи значения начального заполнения счетчика 14 выполняется запись значения 2n-k в вычитающий счетчик 5; далее с первого выхода коммутатора 1 на управляющий вход многоканального мультиплексора 3 подается значение кортежа переменных разложения xl, x2, …, xk, которое определяет выбор соответствующей группы коэффициентов полинома разложения Р(х1, х2, …, хk, Х); далее коэффициенты полинома разложения подаются на входы мультиплексора 6; далее выполняется вычисление полинома путем итеративного вычисления полинома по схеме Горнера, где распределитель тактовых импульсов 4 обеспечивает последовательное срабатывание вычитающего счетчика 5, двухвходового многоразрядного сумматора по модулю 8 и двухвходового многоразрядного умножителя по модулю 9, при этом вычитающий счетчик определяет последовательный выбор мультиплексору 6 коэффициентов полинома разложения, а двухвходовый многоразрядный сумматор по модулю 8 и двухвходовый многоразрядный умножитель по модулю 9 выполняют итеративное вычисление полинома разложения Р(х1, х2, …, хk, Х); при достижении вычитающим счетчиком 5 значения «0» на все входы многовходового логического элемента ИЛИ-НЕ 7 подается значение «0», которое инвертируется в значение «1» и передается на управляющий вход выходного регистра 10, который выполняет запись значения вычисления системы булевых функций, представленной полиномом Р(х1, х2, …, хk, Х), поступающего с выхода двухвходового сумматора по модулю 8, и передает его на выходы выдачи значений булевых функций 15.1-15.d.
записываются в блок памяти хранения значений коэффициентов 2.2k, также со входа подачи значения начального заполнения счетчика 14 выполняется запись значения 2n-k в вычитающий счетчик 5; далее с первого выхода коммутатора 1 на управляющий вход многоканального мультиплексора 3 подается значение кортежа переменных разложения xl, x2, …, xk, которое определяет выбор соответствующей группы коэффициентов полинома разложения Р(х1, х2, …, хk, Х); далее коэффициенты полинома разложения подаются на входы мультиплексора 6; далее выполняется вычисление полинома путем итеративного вычисления полинома по схеме Горнера, где распределитель тактовых импульсов 4 обеспечивает последовательное срабатывание вычитающего счетчика 5, двухвходового многоразрядного сумматора по модулю 8 и двухвходового многоразрядного умножителя по модулю 9, при этом вычитающий счетчик определяет последовательный выбор мультиплексору 6 коэффициентов полинома разложения, а двухвходовый многоразрядный сумматор по модулю 8 и двухвходовый многоразрядный умножитель по модулю 9 выполняют итеративное вычисление полинома разложения Р(х1, х2, …, хk, Х); при достижении вычитающим счетчиком 5 значения «0» на все входы многовходового логического элемента ИЛИ-НЕ 7 подается значение «0», которое инвертируется в значение «1» и передается на управляющий вход выходного регистра 10, который выполняет запись значения вычисления системы булевых функций, представленной полиномом Р(х1, х2, …, хk, Х), поступающего с выхода двухвходового сумматора по модулю 8, и передает его на выходы выдачи значений булевых функций 15.1-15.d.
Таким образом, в отличие от прототипа технический эффект предложенного устройства достигается путем сокращения количества двухвходовых многоразрядных умножителей по модулю с 2n-k (в случае прототипа) до 1-го (в случае заявленного устройства) и замены 2n-k входового многоразрядного сумматора по модулю (в случае прототипа) на двухвходовый многоразрядный сумматор по модулю (в случае заявленного устройства) и введения распределителя тактовых импульсов, вычитающего счетчика, многовходового логического элемента ИЛИ-НЕ, выходного регистра.
Предложенное устройство может быть реализовано с использованием современной элементной базы программируемых логических интегральных схем фирм Altera, Xilinx.
Литература
1. RU, №2461868, 2012.
2. RU, №2586574, 2015.
| название | год | авторы | номер документа |
|---|---|---|---|
| МОДУЛЯРНЫЙ ПОЛИНОМИАЛЬНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2015 |
|
RU2586575C1 |
| ПОЛИНОМИАЛЬНЫЙ МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ С ОБНАРУЖЕНИЕМ ОШИБОК | 2015 |
|
RU2586574C1 |
| МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2007 |
|
RU2373564C2 |
| АРИФМЕТИЧЕСКИЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2011 |
|
RU2461868C1 |
| САМОПРОВЕРЯЕМЫЙ МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ ЛОГИЧЕСКИХ ФУНКЦИЙ | 2009 |
|
RU2417405C2 |
| Устройство поддержки защищенных логических вычислений | 2016 |
|
RU2625049C1 |
| Адаптивное к экстренным ситуациям устройство передачи телеметрической информации | 2017 |
|
RU2654169C1 |
| Модулярное устройство вычисления систем линейных алгебраических уравнений | 2015 |
|
RU2611963C1 |
| САМОПРОВЕРЯЕМЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2012 |
|
RU2485575C1 |
| Устройство для вычисления полиномов | 1987 |
|
SU1509878A1 |
Изобретение относится к вычислительной технике и может быть использовано для аппаратной реализации криптографических примитивов. Технический результат изобретения заключается в обеспечении вычисления в системе остаточных классов. Технический результат достигается за счет логического вычислителя в системе остаточных классов, который содержит коммутатор, 2k блоков памяти хранения значений коэффициентов, многоканальный мультиплексор, распределитель тактовых импульсов, вычитающий счетчик, мультиплексор, многовходовый логический элемент ИЛИ-НЕ, двухвходовый многоразрядный сумматор по модулю, двухвходовый многоразрядный умножитель по модулю, выходной регистр, n входов подачи значений булевых переменных, вход подачи значения количества переменных разложения, вход подачи значений коэффициентов полиномов разложения, вход подачи значения начального заполнения счетчика, d выходов выдачи значений булевых функций. 1 ил.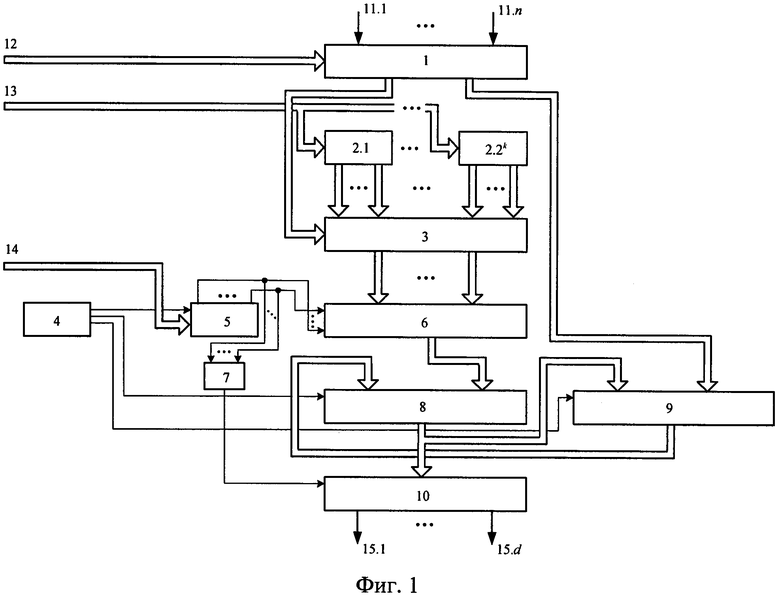
Логический вычислитель в системе остаточных классов, содержащий коммутатор, информационные входы которого с 1-го по n-ый подключены соответственно к n входам подачи значений булевых переменных, являющимся входами устройства, управляющий вход которого подключен к входу подачи значения количества переменных разложения, являющемуся входом устройства; 2k блоков памяти хранения значений коэффициентов, входы которых подключены к входу подачи значений коэффициентов полиномов разложения, являющемуся входом устройства, а 2n-k выходов каждого из блоков памяти хранения значений коэффициентов подключены соответственно к группам информационных входов многоканального мультиплексора, управляющий вход которого подключен к 1-му выходу коммутатора; двухвходовый многоразрядный умножитель по модулю, 2-ой информационный вход которого подключен к 2-му выходу коммутатора; d выходов выдачи значений булевых функций, являющихся выходами устройства, отличающийся тем, что введены распределитель тактовых импульсов, 1-ый выход которого подключен к управляющему входу вычитающего счетчика, 2-ой выход которого подключен к управляющему входу двухвходового многоразрядного сумматора по модулю, 3-ий выход которого подключен к управляющему входу двухвходового многоразрядного умножителя по модулю; вход подачи значения начального заполнения счетчика, являющийся входом устройства, который подключен к входу вычитающего счетчика; мультиплексор, управляющие входы с 1-го по (n-k)-ый которого соответственно подключены к выходам вычитающего счетчика, информационные входы с 1-го по 2n-k-ый которого соответственно подключены к 2n-k выходам многоканального мультиплексора, а выход подключен к 2-му информационному входу двухвходового многоразрядного сумматора по модулю, при этом 1-ый вход двухвходового многоразрядного сумматора по модулю подключен к выходу двухвходового многоразрядного умножителя по модулю, а выход подключен к 1-му информационному входу двухвходового многоразрядного умножителя по модулю и информационному входу выходного регистра, при этом выходы с 1-го по d-ый выходного регистра подключены соответственно к d выходам выдачи значений булевых функций; многовходовый логический элемент ИЛИ-НЕ, (n-k) входов которого подключены соответственно к (n-k) выходам вычитающего счетчика, а выход подключен к управляющему входу выходного регистра.
| ПОЛИНОМИАЛЬНЫЙ МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ С ОБНАРУЖЕНИЕМ ОШИБОК | 2015 |
|
RU2586574C1 |
| ЛОГИЧЕСКИЙ ВЫЧИСЛИТЕЛЬ | 2006 |
|
RU2324219C1 |
| ЛОГИЧЕСКИЙ ВЫЧИСЛИТЕЛЬ | 2002 |
|
RU2227931C1 |
| САМОПРОВЕРЯЕМЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2015 |
|
RU2579991C1 |
| ЛОГИЧЕСКИЙ ВЫЧИСЛИТЕЛЬ | 2012 |
|
RU2504826C1 |
| Устройство для закрепления лыж на раме мотоциклов и велосипедов взамен переднего колеса | 1924 |
|
SU2015A1 |
Авторы
Даты
2017-12-04—Публикация
2016-10-07—Подача