сл
с


| название | год | авторы | номер документа |
|---|---|---|---|
| Головоломка | 1989 |
|
SU1703154A1 |
| Объемная головоломка | 1989 |
|
SU1718998A1 |
| Головоломка | 1989 |
|
SU1674889A1 |
| Пространственная головоломка | 1987 |
|
SU1470312A1 |
| Комбинированная головоломка | 1989 |
|
SU1745275A1 |
| Объемная головоломка | 1989 |
|
SU1725937A1 |
| Объемная игра-головоломка "Пиракуб | 1987 |
|
SU1567232A1 |
| "Головоломка "Иванов еж" | 1990 |
|
SU1766444A1 |
| ОБЪЕМНАЯ ИГРА-ГОЛОВОЛОМКА | 2009 |
|
RU2403946C1 |
| Головоломка Генеля | 1987 |
|
SU1583118A1 |




Сущность изобретения: головоломка представляет собой набор из шести брусков квадратного сечения с тремя одинаковыми пазами по меньшей мере в пяти из них, шести по меньшей мере четырехгранных пирамид, устанавливаемых в пазах брусков для изменения их конфигурации, и средств фиксации пирамид в пазах. Двугранные. прямоугольные пазы чередуются вдоль бруска с образованием ребер между ними и их грани расположены под углом 45° к ребрам бруска. Необходимо сконструировать некоторую расстановку различных пазов в брусках, при которой возможна сборка элементов игры в симметричную объемную крестообразную фигуру. В этой фигуре пары брусков соединены ребрами. 11 ил
Изобретение относится к конструкциям занимательных игр.
Известна сборная пространственная головоломка, содержащая шесть игровых брусков квадратного сечения, соединенных между собой в объемную крестообразную фигуру без пустот внутри, по меньшей мере пять из которых имеют в средней части установочные пазы, а также средства для изменения конфигурации пазов, выполненные в виде многогранных элементов.
Однако известная головоломка недостаточно занимательна
Цель изобретения - повышение занимательности.
Указанная цель достигается тем, что в сборной объемной крестообразной фигуре бруски, число которых шесть, в парах касаются друг друга продольными ребрами, а образующиеся при этом углы между их гранями прямые. Пазы же в средней части по
меньшей мере пяти брусков представляют собой три двугранных выреза, а формирующие их многогранные элементы - четырехгранные пирамиды.
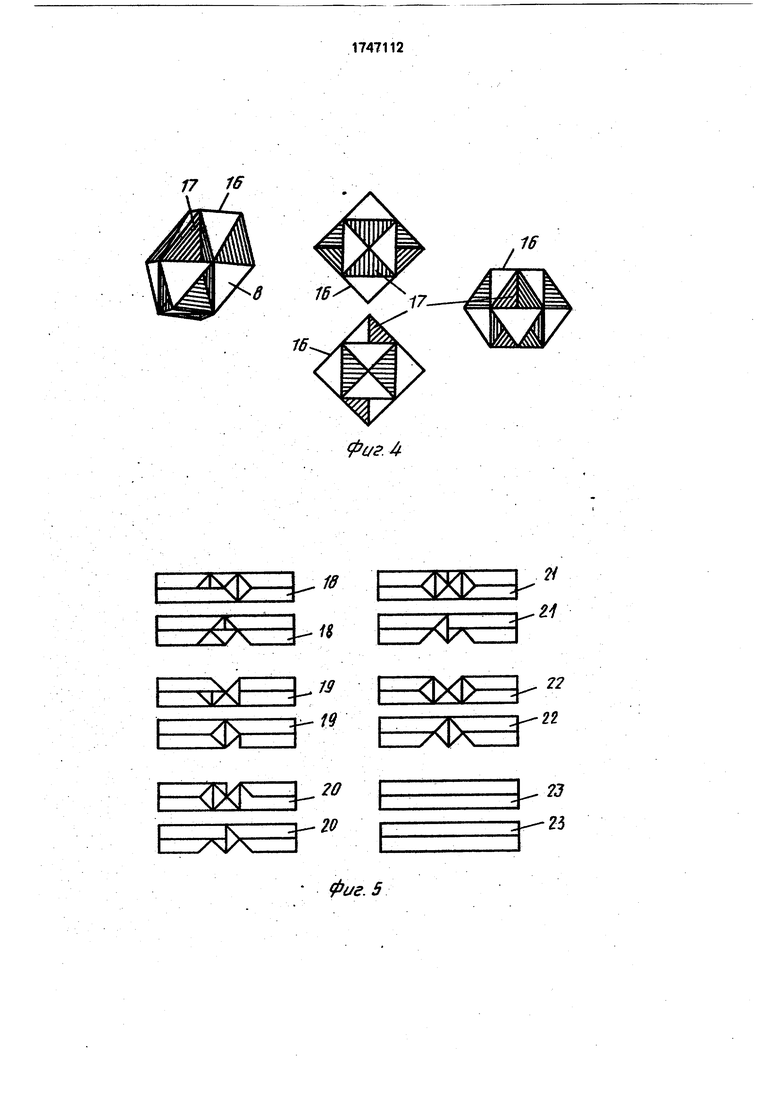
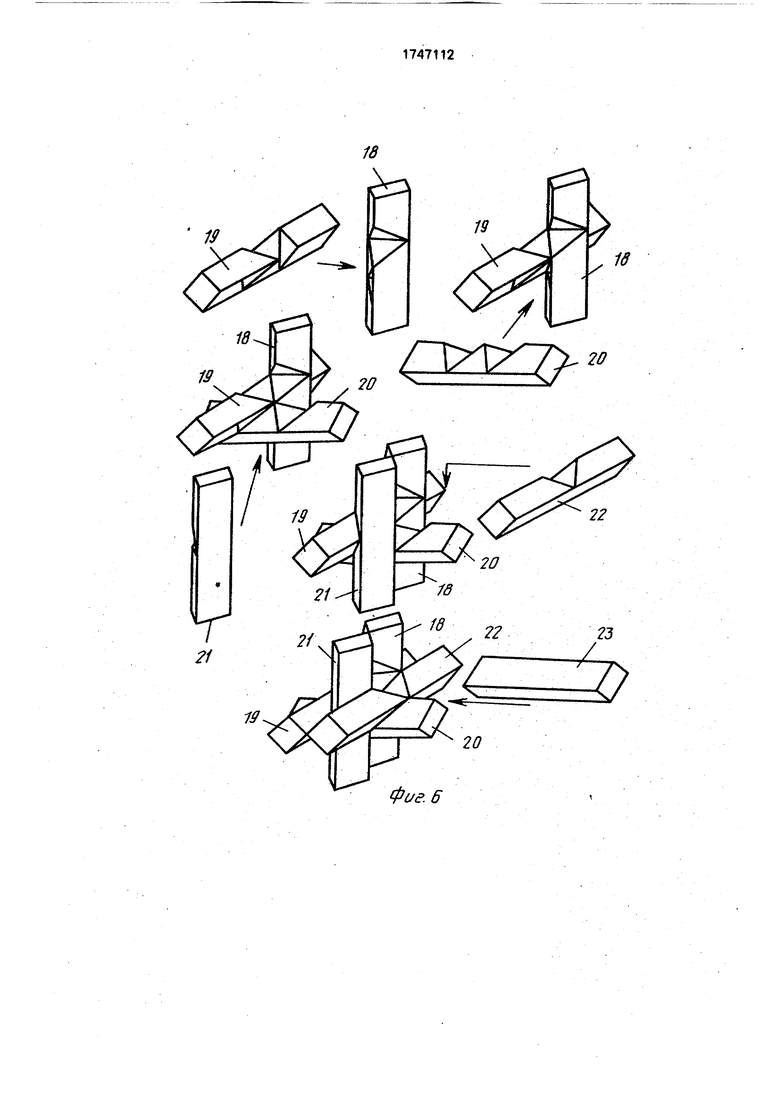
На фиг.1 изображена головоломка в сборе; на фиг.2 - стандартный брусок со свободными пазами и пирамида, устанавливаемая в этих пазах, виды спереди и сбоку; на фиг.З - паз в бруске и пара сложенных гранями пирамид, заполняющая этот паз, примеры установки в пазу одной пирамиды, виды спереди и сверху; на фиг 4 - фигура парных пересечений, образующая ромбододекаэдр с симметрично расположенными в нем выемками, виды спереди, сбоку и в направлении между фронтальным и вертикальным под углом 45° к ним, на фиг.5 - один из вариантов формирования пазов брусков, позволяющих собрать их в крестообразную фигуру (один из брусков без пазов); на фиг.6 - пооперационная сборка ежа
V N VI
ю
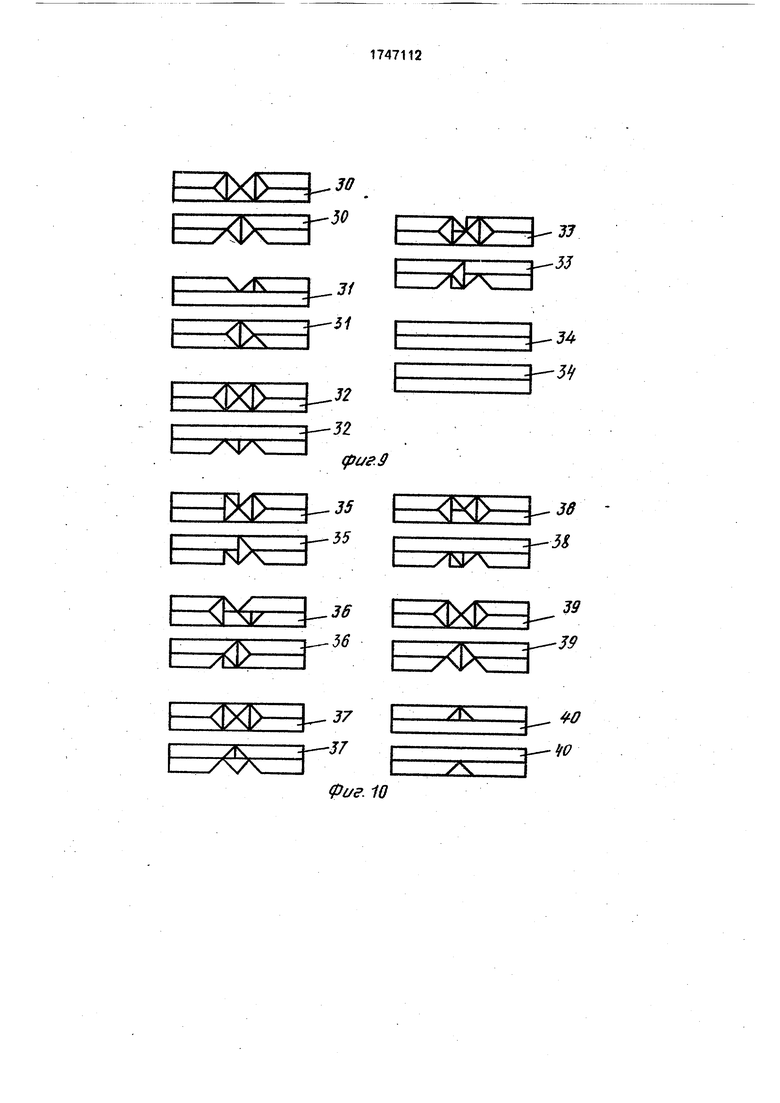
из такого комплекта; на фиг,7 - один из получаемых комплектов брусков, собираемых также тройками; на фиг.8 - порядок его сборки; на фиг.9 - вариант формирования пазов брусков, в котором два бруска одинаковы (брусок 30), один брусок имеет два паза; на фиг. 10 - вариант комплекта брусков, все из которых имеют пазы; на фиг. 11 - средства и порядок крепления пирамид в пазах: отверстия в пазах брусков и пирамидах, штыри крепления, виды спереди и сверху.
Предлагаемая закономерность формирования пазов брусков фигуры 1 (фиг.1), не имеющей пустот внутри, строится следующим образом.
Стандартный брусок 2 имеет три двугранных паза, два крайних из которых (пазы 3} параллельны, а третий (паз 4) расположен между ними и повернут относительно них на 90° вокруг продольной оси бруска. Каж- дый такой паз пересекает только две грани бруска так, что стороны его образуются из двух одинаковых треугольников, вершины которых располагаются на ребрах бруска (фиг.2), а угол между плоскостями этих треугольников прямой. Таким образом, плоскости, совпадающие с гранями паза 5, пересекают ребра бруска под углом 45е. При этом ребра, образованные пересечением смежных граней соседних пазов, лежат в плоскости, совпадающей с продольной гранью бруска, В качестве стандартных брусков служат одинаковые четырехгранные пирамиды 6. Эти средства, изменяющие конфигурации пазов 7, легко получить рассечением большой пирамиды 8 с четырьмя одинаковыми треугольными гранями и двумя прямыми двугранными углами при противолежащих ребрах 9, заполняющей полностью паз 7, ее плоскостью симметрии 10 надвое. При этом грань 11 пирамиды б, принадлежащая этой плоскости, представляет собой прямоугольный треугольник, половину поперечного сечения бруска. Угол между гранью 11 и ребром 12 прямой. Дополнение паза бруска такой пирамидой 6 возможно двумя способами, В одном случае нужно приложить большую грань 13 пирамиды 6 к какой-либо грани паза, в другом случае меньшее ребро 12 пирамиды б - к ребру паза так, чтобы большая грань пирамиды 6 лежала в плоскости грани бруска. В первом случае остается паз, опять же представляющий двугранный желобок 14, но одна из граней которого располагается поперек бруска, во втором - трехгранная выемка 15, одна из граней которой располагается вдоль бруска Упомянутые соответственно поперечные и продольные грани в
пазах 14 и 15 одинаковы - это прямоугольные треугольники, равные половине поперечного сечения брусков. Таким образом, конфигурации пазов после их конструирования могут быть трех видов (пазы 7, 14 и 15). По меньшей мере в пяти из шести игровых брусков имеются три и менее паза в каждом. Они должны позволять собрать все бруски в трехмерную фигуру без пустот внутри, при
0 этом число малых двугранных пазов должно быть равным числу трехгранных пазов 15 на всех вместе взятых брусках (максимальное число тех и других пазов равно трем, при сборке брусков их угловые выступы, образо5 ванные пирамидами 6, входят в подходящие выемки 14 и 15). Пазы 7 при сборке фигуры упираются в углы брусков. Как бы ни формировались пазы брусков для того, чтобы собрать их в крестообразную фигуру,
0 необходимо и достаточно, чтобы математическое множество парных пересечений брусков в фигуре представляло собой вырезанный ромбододекаэдр 16с занимающими половину его объема трехгранными
5 выемками 17(фиг.4). Такой ромбододекаэдр состоит из 12 пирамидв, которые являются пирамидами парных пересечений. Одна из вершин каждой пирамиды располагается в центре симметрии многогранника 16, а три
0 ребра являются смежными с соседними пирамидами. При этом выемки 17 между ними, дополняющие многогранник 16 до ромбододекаэдра, равны пирамидам 8. В совокупности же выемки повторяют описываемую
5 фигуру пересечений и совпадают с ней при симметричном отражении в одной из плоскостей симметрии ромбододекаэдра.
Если сориентировать многогранник 16 пересечений так же, как и сам еж 1 (фиг.4 и
0 1 соответственно), то можно представить, как формируются пазы брусков, На месте каждой пирамиды вырезанного ромбододекаэдра 16 один из пары пересекающихся брусков имеет двугранный паз 7,или же оба
5 бруска имеют один - трехгранную выемку 15, другой - двугранную выемку 14, вместе при сборке составляющие объем пирамиды 8. Так, нетрудно представить расстановку пазов в брусках 18-23 (фиг.5), собираемых в
0 еж (фиг.6), Это один из сотен возможных вариантов комплектов из шести брусков, причем в нем брусок 23 выемок не имеет и носит замыкающую функцию. Чтобы разобрать такой еж, необходимо вытолкнуть
5 этот замыкающий брусок вдоль его продольной оси.
Кроме того, возможна сборка ежа сты ковкой двух троек брусков. Например, если
сложить одну тройку из брусков 24-26
(фиг,7) с одной стороны и другую тройку
брусков 27-29 с другой, то их беспрепятственно можно собрать в ежа (фиг.8). Эти же бруски можно сложить и другой парой троек: 25-28 и 24-29, а также последовательной сборкой с замыкающим бруском 29 подобно брускам 18-23 (фиг.5). Сборка последних тройками невозможна.
Для полного представления возможных расстановок пазов различных конфигураций на брусках можно рассмотреть еще два варианта, где в одном комплекте 30-34 (фиг.9) имеются брусок 31с числом выемок, меньшим трех, два одинаковых бруска 30 и замыкающий брусок 34, а в другом комплекте 35-40 (фиг. 10) имеется брусок 40 лишь с одной выемкой и отсутствует замыкающий брусок. Сборка последнего уже невозможна последовательными приложениями брусков, а только - групповыми типа тройка - тройка (фиг.8).
Пример. Набор деталей головоломки следующий: шесть одинаковых брусков с тремя прямоугольными парами в каждом бруске 41; 12 пирамид 42 со средствами 43 для фиксации пирамид в пазах брусков. Фиксаторы 43 представляют собой небольшие штыри, плотно входящие в сквозные отверстия 44 в пирамидах 42 и в отверстия 45 в пазах брусков 41. При установке пирамид 42 в пазах два их отверстия 44 прикладываются или к отверстиям 46 на одной грани паза, или же к паре отверстий 47 разных граней. В первом случае пирамиды прикладываютвя полностью к одной из граней паза, в другом случае выдвинутые с обратной стороны отверстий штыри 48 позволяют закреплять пирамиды в перевернутом положении ребром к ребру паза. При
фиг. 1
монтаже деталей должны быть использованы все пирамиды, чтобы задача сборки ежа без густот внутри выполнялась Очевидно, если собрать шесть пирамид на одном бруске, он становится замыкающим (брусок без пазов), другие же шесть пирамид формиру- ют пазы остальных брусков.
Формула изобретения Сборная пространственная головоломка, содержащая шесть игровых брусков
квадратного сечения, соединенных между собой в объемную крестообразную фигуру без пустот внутри, по меньшей мере пять из которых имеют в средней части установочные пазы, а также средства для изменения
конфигурации пазов, выполненные в виде многогранных элементов, отличающая- с я тем, что, с целью повышения занимательности, каждый брусок имеет три паза, причем пазы брусков имеют прямоугольную
двугранную, форму и образованы так, что ребро паза пересекает два несмежных продольных ребра бруска и перпендикулярно к ним, а плоскости, совпадающие с гранями паза, пересекают ребра бруска под углом
45°, при этом ребра, образованные пересечением смежных граней соседних пазов, лежат в плоскости, совпадающей с гранью бруска, а заполняющие пазы брусков средства для изменения конфигурации пазов
представляют собой одинаковые четырехгранные пирамиды, выполненные так, что две пирамиды заполняют паз полностью, при этом пары брусков в крестообразной фигуре соединены продольными ребрами
так, что между их гранями образуется прямой угол.
/
Jj.
S
3 H 3
N
13
15
Фиг.З
- Ч
С
Л7 U
в
ф17 16
зйВ-
19
BDrf
Фиг. 5
16
РагЛ
У М
Р
22
1i
19
fe
/
23
3
20
Фие.6
ix-я-
2S
зхг
f/f I 26
27
F-ФФ-425 IжL.
3- Ј-29
Фиг 7
29
л
7&
36
г 10
r
34 М
7
/Тч J. 40
W
Г
4-2 42
45 45
F
Фиг. 11
М
4-8 43
48
44
ч
42
42
| Головоломка | 1983 |
|
SU1158209A1 |
| Способ приготовления сернистого красителя защитного цвета | 1915 |
|
SU63A1 |
Авторы
Даты
1992-07-15—Публикация
1990-02-09—Подача