Известно, что уравнение Брегга в квадратичной форме тетрагональной системы, имеющее вид; . ., ,, .- {К - + К- , ,,.. 5,.,,,).. .(1) преобразовывается в уравнение прямой линии, отсекающей на осях координат отрезки под углом Q,-,--J,.(2) л. X. г:. -. а При известных я, с, д и О можно построить график и координаты точек пересечения прямых (2), (4) и (5) для каждого sin-H дают нам искомые индексы /г, /е, /. В случае ромбической системы квадратичная форма имеет вид: -п - Г- : К- I М/c s,n-()(--,, . .(6) Преобразовываем уравнение (6) в уравнение:Q.- -.-ЬЛ + г, - . . .(7), а уравнение зеооразовываем в уравнение Q.- :-т-/;. где /.,-вектор, компоненты которого у., и г., выбираем так, чтобы их проекции на ось / равнялись соответственно у., и ;г., из уравнения (7). Таким образом, исходя из уравнения (8), можно построить график на плоскости и проиндицировать ромбическую систему. В случае гексагональной системы ее преобразовывают в ортогексагональную систему и индицируют как ромбическую. С целью не только индицирования всех вышеназванных систем, но также и определения параметров таковых, можно построить воспроизводящий кристаллическую систему график, путем вращения или передвижения компонентов которого возможно перейти к индицированию или определению параметров одной из остальных трех кристаллических систем. Такой системой является кубическая система, которую можно рассматривать, как частный случай ромбической.
Квадратичная форма кубической системы в данном случае примет вид:
( + 44-4) . .(9)
4 я- а- а /
Из уравнения (7) при h следует:
(10)
т. е. отрезки, откладываемые на осях координат, будут равны.
Преобразовываем уравнение (9) в уравнение:
Q... - - (П)
где
Q.. .
Принимая во внимание уравнение (8) и рассматривая пока только случай индицирования, построим прямоугольник из тоненьких планок, одну сторону которого жестко закрепим к остову аппарата. Вершины прямоугольника скрепим шарнирно так, чтобы он мог принять форму параллелограма. На обеих сторонах прямоугольника, перпендикулярных к закрепленной стороне, откладываем значение Л:;. Через точки // проводим тонкие нити, закрепленнь е шарнирно в данных точках так, чтобы при преобразовании прямоугольника в параллелограм, эти нити всегда были параллельны жестко закрепленной стороне.
Жестко закрепленную планку примем за ось /, а сторону, на которой отложены значения Л,-за ось к.
Построим еще ромб тоже из тоненьких планок, одна вершина которого может вращаться вокруг точки А, жестко прикрепленной к остову аппарата и лежащей на оси л, на определенном расстоянии от центра координат.
Верщины ромба соединяем шарнирно так, чтобы в идеальном случае ромб мог превратиться в горизонтальную или вертикальную линию.
Диагональ ромба, перпендикулярную к оси А , примем за ось /.
На двух противоположных сторонах ромба откладываем значения у, и соединяем их планками шарнирно.
То же самое делаем с z на двух остальных сторонах ромба.
Точки пересечения прямых j и .г; скрепляем шарнирно.
При нормальном положении графика, т. е. когда параллелограм имеет вид прямоугольника, а диагональ ромба перпендикулярна к оси х,, исходя из уравнения (11), можно проиндицировать любую кубическую систему с параметром а..
При индицировании кристаллической тетрагональной системы преобразовываем уравнение (11) в уравнение (12):
J- . -02)
в данном случае ромб оставляем в нормальном положении, а прямоугольнику придае.м форму параллелограма.
Требуемый угол :i определяем из уравнения (13):
(13)
cos .-i
Для индицирования кристаллической ромбической системы исходим из следующих соображений- Предположим, что индицируем какую-либо кубическую систему с параметром тогда ромб и прямоугольник находятся в нулевом положени-.
Выберем какой-либо sin-tj из отложенных на графике, которому соответствуют определенные А, k и /.
Повернем ромб вокруг точки Л так, чтобы данному sin-B на графике соответствовали индексы k и /, а прямоугольник превратим в такой параллелограм, чтобы данному sin-l;) соответствовал индекс h .
Для данного значения sin-O с изменением индексов, исходя из уравнения (9), должны соответственно изменяться и параметры.
Таким образом, благодаря подвижности осей координат, можно перейти от индицирования кубических кристаллов к индицированию ромбических кристаллов.
Из этого следует, что если вывести несколько уравнений, связьшающих О) и И, где Я-угол между диагональ:-о
ромоа при нормальном положении и диагональю повернутого ромба, а со- разность между тупым углом параллелограма и прямым углом прямоугольника (с параметрами а., Ь. и с. соответствующими ромбической системе), то при известных и., Ь. и (Г.можно всегда найти соответствующие им а,, (W и .: и таким образом индицировать кристаллы ромбической системы.
Уравнение, связывающее выщеописанные величины, будет следующее:
aj а If, 1. с cos- . (14) cos cosvi
где «1--Yi - углы между сторонами ромба и его диагональю при нормальном его положении, Яо -угол между диагональю ромба, при нормальном его положении, и одной из сторон ромба при повороте такового, -9-угол между диагональю ромба, при нормальном его положении, и второй из -сторон ромба при том же самом повороте ромба.
Задаваясь углом а, и зная, что
а,-г-7 (15)
можно из уравнения (14), взяв отно. иtCOS -д.,
шение -.,--- , определить cos-,-., «V cos-;.,Iи COS:;., и таким образом определить искомые а, и 3.
Угол о можно определить, исходя из уравнения (16):
W у., - а, YI - -, . - (1 б).
При индицировании гексагональной системы поступаем так, как было указано выше.
Дпя того, чтобы приспособить данный аппарат также и для определения параметров, необходимо выбрать какое-то постоянное (и ), как множитель для левой части уравнения (11) для всех рассмотренных нами систем. Для того, чтобы найти значения а., Ь и с., необходимо сжимать, раздвигать или поворачивать ромб, преобразовывать прямоугольник в параллелограм до тех пор, пока не найдем искомых точек пересечения для всех отложенных прямых из уравнения (8).
Дпя этого необходимо построить
еще один ромо, расположенный по отношению к прямоугольнику симметрично первому ромбу .и соответствующие точки пересечения прямых: У1, kl, zl ll обоих ромбов соединить стальными проволоками щарнирно.
Кроме того необходимо под каждым ромбом поместить эбонитовую или медную рамку, на которой помещаются щкалы со значениями а. и Ь.
для тетрагональной и ромбической систем.
Шкала со значением с- помещается под прямоугольником.
Шкала для тетрагональной системы, где а. Ь., откладывается на прямой, параллельной диагонали ромба при нормальном его положении.
Шкалы для ромбической системы откладываются по дугам, описьжаемым вершиной диагонали ромба при его повороте.
При построении шкалы для тетрагональной системы нужно исходить из уравнения
i
COS-у -
.; (17)
., I
При построении шкалы для с. нужно исходить из уравнения (18)
(
cos-..
(18)
о о
При построении щкалы для ромбической системы, где а.., нужно исходить из уравнений (14) и (16), задаваясь углами «..
Каждое найденное aj из уравнения (17) рассматриваем как af, в уравнении (14).
Для сокращения размеров аппарата и увеличения интервала значений параметров, не уменьщая точности определения последних, необходимо создать одну шкалу с интервалом
.-а
параметров от 2,5 А до 5 f, а втооо
рую-ОТ 5Д ДО 10 f.
Для первой а 2,5 ft и для второй On 5f.
.Соответственно этим шкалам необ- . ходимо установить две номограммы с линиями уравнения (18), нанесенными на двух прямоугольных равно- ; бедренных целлюлоидных треугольни- ; ках, каждый из которых вставляется | в паз, сделанный в жестко закреплен- I ной планке прямоугольника.i
Катет первого треугольника равен (2,5) и второго-(5) .I
Для сокращения расчетов, связан- i ных с нахождением sin9, необходимо на целлюлоидных треугольниках нанести шкалы, где каждому значе- нию 2г, измеренному на дебайграмме с точностью до 0,5 мм, соответствует соответствующее значение sin-B.
Таким образом, вся работа по определению параметров сводится к тому, чтобы измерить значение 2г на дебай- ; грамме, нанести линии уравнения (8) на треугольник и привести подвижной график в соответствующее положение. ;
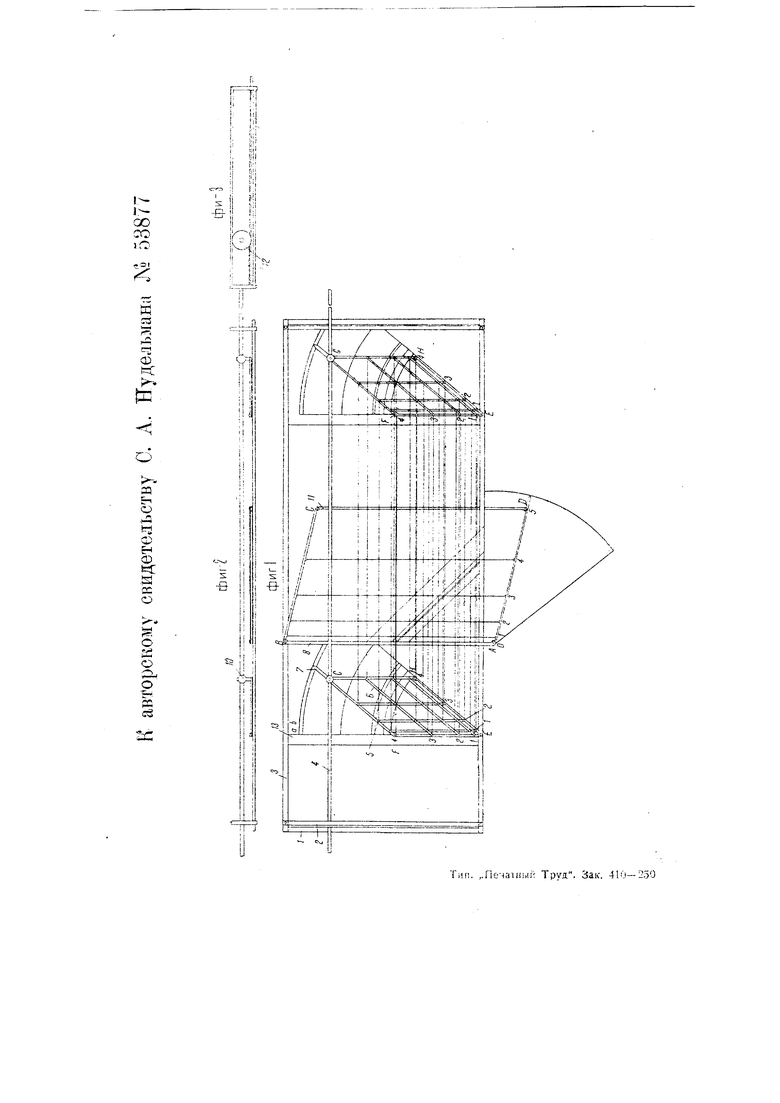
Примерная форма выполнения прибора приведена на фиг. 1, 2 и 3.;
Предлагаемый прибор представляет : собой жесткую раму, состоящую из двух продольных планок 5 и из двух поперечных планок 7. К раме прикреплен шарнирный ромб EFGH, соста- вленный из четырех планок 5, соеди- ; ненных между собой щарнирами так, что углы ромба являются переменными.
Ромб в своей вершине Е соединен с нижней продольной планкой 3 рамы щарнирно болтом /, который является осью вращения ромба.
На каждой планке 5. просверлено | по пяти отверстий; расстояния между начальным в точке Е и каждым из последующих находятся в отношении 1 :4:9:1б.
Эти отверстия обозначены на чер- j теже цифрами О-/-2-3-4. На ромбе имеются еще шесть планок 6, шарнирно соединенных с планками 5 и между собой. Три планки б соединяют отверстия /, 2 и 5 одной пары { противоположных планок 5.
Остальные три планки 6 соединяют отверстия /, 2 и 5 другой пары противоположных планок 5. Таким образом, планки 6 образуют девять точек пересечения между собой и двенадцать точек пересечения с планками 5.:
Симметрично с первым ромбом к нижней продольной планке рамы прикреплен шарнирно аналогичный первому второй ромб. Все точки пересечения планок 5 VI 6 обоих ромбов,, (а их на каждом ромбе 25) соединены между собой двумя рядами тоненьких стальных нитей так, что каждая точка пересечения планок одного ромба соединена с точкой пересечения соответствующих планок второго ромба.
Параллелограм ABCD состоит из планки 8, жестко скрепленной с продольными планками рамы, пары (нижняя и верхняя) планок 13 (CD) и двух пар (нижняя и верхняя) планок 9 (ВС и AD}. Каждая пара планок 9 соединена в точках А и В шарнирно с планкой 8 и в точках С и D с планками // так, что углы параллелограма являются переменными. В каждой планке 9 просверлены шесть отверстий, обозначенные цифрами 0-1-2-3-4-5. Отверстия О--/-2-3-4-5 планок 9 соединены между собой тонкими стальными нитями; при этом очевидно, что при изменении углов параллелограма эти нити всегда остаются параллельными планке 8 (--i-B).
В точке С параллелограма жестко укреплен указатель 7, скользящий по шкале для определения параметра с.
Изменение углов параллелограма происходит только в одной плоскости. На валу 4 жестко насажены две муфты Ю, соединяющие вал с шарнирами вершин ромбов в точках С. Расстояние между соединительными муфтами 10 равно расстоянию между болтами, соединяющими вершины ромбов с нижной продольной планкой 3 рамы.
На каждой из соединительных муфт жестко насажен указатель 7, скользящий по шкале параметров d и Ь. При передвижении вала 4 параллельно самому себе последний скользит на роликах 72 по направляющим, скрепленным с планками 7; при этом указатели ромбов скользят по шкалам для определения а и Ь.
Вал 4 также может передвигаться вверх и вниз по направлению, перпендикулярному к продольным планкам 3. При любом передвижени вала, стороны обоих ромбов остаются параллельными.
Два ряда нитей, соединяющих точки пересечения обоих ромбов, расположены в двух плоскостях и проходят между верхней и нижней планками 7/. Планка (АВ) находится между двумя рядами нитей.
. Шкала для определения параметров а расположена на целлюлоидной или медной доске /5, выполненной в виде прямоугольника, жестко скрепленного с остовом аппарата и находящегося под ромбом.
На линии, перпендикулярной к про-дольным планкам рамы и пересекающей точку Е ромба, расположена
щкала с делениями в А от 2,5F
до 5 fl через 0,01 fl сверху вниз. От каждого деления проведены дуги, центром которых являются точки Е.
На дугах нанесены деления в fl для параметра а ромбической системы.
Такая же щкала помещена и под вторым ромбом с той лишь разницей, что на данной щкале на дугах нанесены деления для параметров b ромбической системы.
Шкала для определения параметрам состоит из медной доски, имеющей форму сектора и жестко скрепленной с нижней продольной планкой рамы.
На дуге сектора нанесены деления
в Д от 2,5 Д до 5 Л через 0,01 А. Шкала значений sin-H нанесена на целлюлоидном, равнобедренном прямоугольном треугольнике, который своим катетом вставляется в паз в планке 8 (АВ) и находится между двумя рядами нитей, соединяющих точки пересечения планок 5 и б обоих ромбов.
Предмет изобретения.
Прибор для индицирования дебайграмм и определения параметров, отличающийся тем, что, с целью индицирования и определения параметров как кубических, так и тетрагональньг;, ромбических и гексагональных кристаллических систем, он состоит из двух соответственно расположенных на общей основной раме и поворотных вокруг одной из их верщин, тождественных и связанных в определенных их точках системой жестких тяг, щарнирных ромбов и одного шарнирного параллелограма, укрепленного одной из своих сторон в той же раме.
2.Форма выполнения прибора по п. 1, отличающаяся тем, что шарнирные ромбы EFGH, состоящие из четырех планок 5, вершинами своими поворотно закреплены в нижней планке основной рамы и снабжены шарнирно соединенными как с планками 5, так и между собой в каждом ромбе, соответственно размещенными параллельно сторонам ромба, тягами 6,. и все соответствующие шарниры обоих ромбов соединены между собой двумя рядами стальных нитей.
3.Форма выполнения прибора по пп. 1 и 2, отличающаяся тем, что параллелограм ABCD прикреплен планкой АВ к верхней и нижней планкам основной рамы, и к планкам ВС и АО в соответствующих местах на шарнирах прикреплены тонкие стальные нити параллельно планкам АВ.
4.В приборе по пп. 2 и 3 применение на валу 4 жестко насаженных муфт /О, соединяющих шарниры ромбов с валом 4, устроенным подвижным по боковым планкам основной рамы.
5.В приборе по пп. 2-4 применение укрепленных на муфтах JO указателей 7, скользящих по соответственным образом градуированным шкалам.
6.В приборе по пп. 2-5 применение на нижней планке параллелограма ABCD указателя для отсчета по соответствующей шкале.




| название | год | авторы | номер документа |
|---|---|---|---|
| ПРИБОР ДЛЯ ВЫЧЕРЧИВАНИЯ ПРОЕКЦИИ ПОВЕРХНОСТИ СПИРАЛИ | 1937 |
|
SU56100A1 |
| Прибор для вычерчивания кривых | 1990 |
|
SU1729814A1 |
| Погрузчик | 1938 |
|
SU58577A1 |
| Накладной кондуктор | 1986 |
|
SU1355372A1 |
| ДВИЖИТЕЛЬ ТРАНСПОРТНОГО СРЕДСТВА | 1997 |
|
RU2124449C1 |
| Прибор для вычерчивания дуги каппы | 1989 |
|
SU1678646A1 |
| Трансформируемый каркас | 1980 |
|
SU968238A1 |
| Прибор для масштабных измерений и кадрировки оригиналов иллюстраций | 1987 |
|
SU1525432A1 |
| Прибор для вычерчивания дуг окружностей | 1950 |
|
SU88147A1 |
| Прибор для построения эллипса | 1982 |
|
SU1057320A1 |


Авторы
Даты
1938-01-01—Публикация
1935-09-11—Подача