Предлагаемое изобретение состоит в особом конструктивном выполнении уже известного прибора для вычерчивания проекции поверхности спирали, снабженного эллипсографом, установленным на подвижной вдоль чертежной плоскости каретке.
Прибор предназначается для построения проекции спирали при конструировании (и соответствующих расчетах) накаливаемых нитей в электрических осветительных лампах. Построение таких проекций необходимо для изучения влияния формы тела накала на излучение и испарение вольфрама и, следовательно, на светоэлектрические характеристики ламп и срок их службы, а также для расчета распределения силы света в потоке, отраженном от зеркала (например, в прожекторах с лампами накаливания).
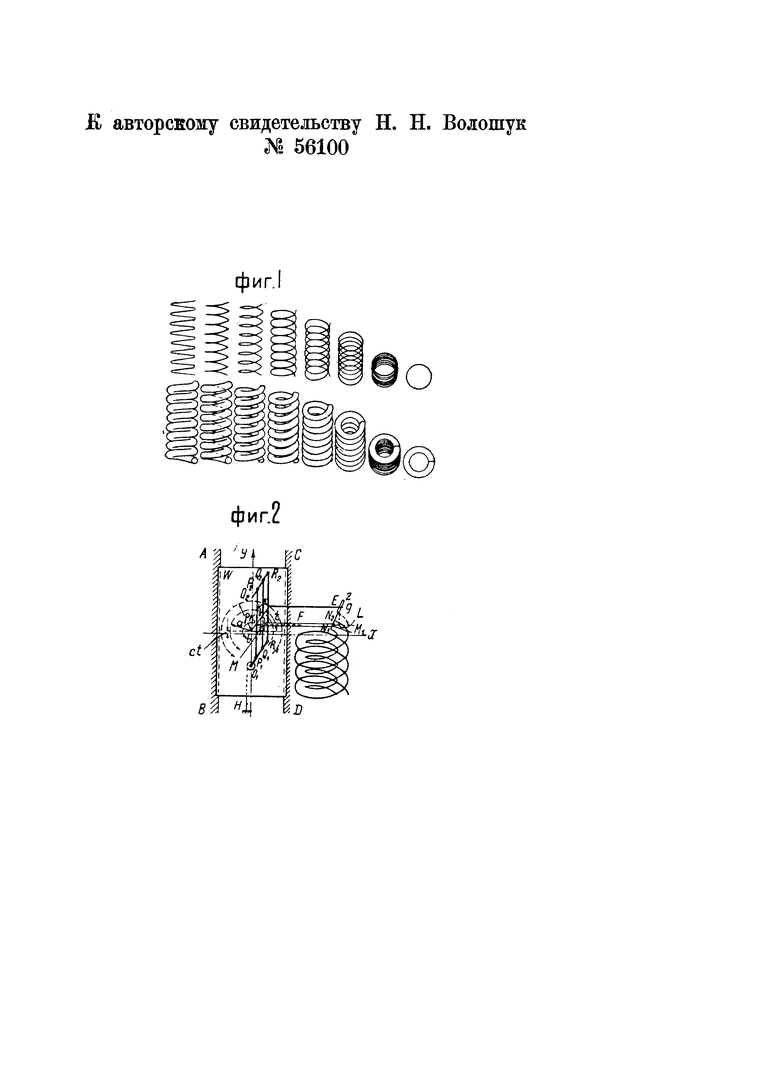
На чертеже фиг. 1 изображает ряд проекций осевой линии свитой в спираль проволоки и проекций поверхности спирали на плоскость, составляющую с осью спирали различные углы, фиг. 2 - схему предлагаемого прибора.
Поверхность всякого калильного тела, свитого из проволоки, можно рассматривать, как огибающую семейства сфер диаметра d, равного диаметру проволоки, центры которых лежат на осевой линии этой витой проволоки. В проекции на плоскость это семейство сфер даст семейство окружностей с центрами, лежащими на проекции осевой линии проволоки. Огибающая этого семейства окружностей и будет проекцией поверхности тела накала.
Таким образом, чтобы получить уравнение проекции поверхности спирали, необходимо:
1) найти уравнение осевой линии проволоки, свитой в спираль,
2) вывести уравнение проекции этой осевой линии свитой в спираль проволоки на плоскость,
3) составить уравнение огибающей семейства окружностей диаметра d, центры которых удовлетворяют уравнению проекции осевой линии.
При составлении уравнения проекции спирали принимаются следующие обозначения:
d=2r - диаметр проволоки
D=2R - диаметр керна (сердечника спирали)
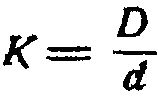 - коэфициент керна
- коэфициент керна
n - число витков спирали в единице длины
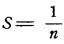 - шаг спирали
- шаг спирали
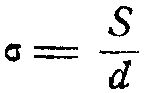 - коэфициент шага спирали.
- коэфициент шага спирали.
Осевой линией свитой в спираль проволоки, как известно, является винтовая линия, параметрические уравнения которой следующие:
x=a cost; y=a sin t; z=mt,
где
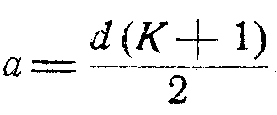
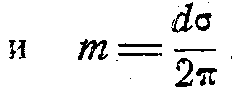
Для изображения проекции этой винтовой линии на плоскость, расположенную под углом ε к плоскости ХУ, достаточно поворотом координатной системы вокруг оси X на угол ε совместить плоскость XY с плоскостью проекции. Пользуясь. общеизвестными формулами поворота координатных осей, можно получить:
x = a cos t
у = a sin t cos ε + mt sin ε.
При обозначении a cos ε = b и m sin ε = c уравнение проекции осевой линии свитой в спираль проволоки выразится в следующем виде:
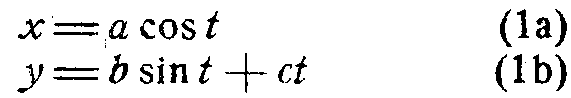
Уравнение семейства окружностей радиуса r (равного радиусу проволоки из вольфрама) с центрами на проекции осевой линии проволоки будет следующее:
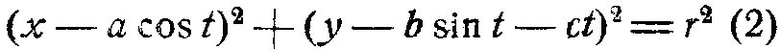
Уравнение огибающей этого семейства можно найти, продиференцировав уравнение (2) по параметру t и решив совместно это уравнение (2) с вновь полученным уравнением относительно х и у
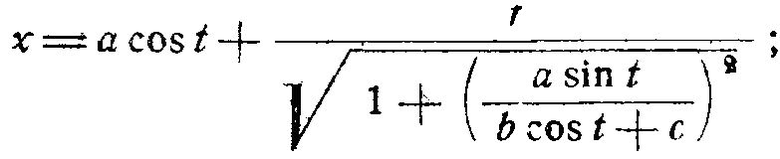
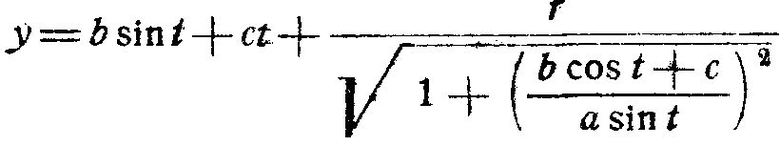
Подставив в последние два уравнения тангенс угла нормали к проекции осевой линии свитой в спираль проволоки:
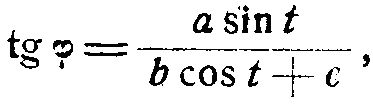
можно получить уравнения огибающей в более простой форме:
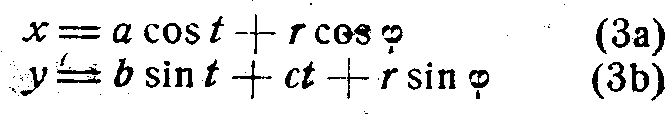
Полученные уравнения и являются уравнениями проекции поверхности спирали на плоскость.
В качестве иллюстрации на фиг. 1 даны проекции осевой линии свитой в спираль проволоки и проекции поверхности спирали (с коэфициентом шага σ=1,5 и коэфициентом керна K=3) на плоскость, составляющую с осью спирали углы 0°, 7°, 15°, 30°, 45°, 60°, 80°, 90°.
Из структуры уравнений (1а) и (1b) проекции осевой линии свитой в спираль проволоки вытекает и способ построения этой проекции.
Действительно, уравнения
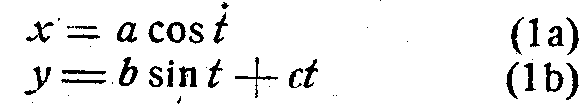
могут быть получены из параметрических уравнений эллипса
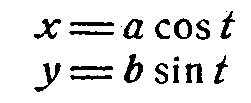
при увеличении ординаты эллипса на длину ct.
Построение эллипса может быть произведено при помощи эллипсографа, увеличение же ординаты нетрудно осуществить смещением эллипсографа относительно чертежной доски на расстояние ct.
Эллипсограф несложной конструкции, основанный на принципе построения эллипса при помощи двух окружностей с радиусами, равными полуосям эллипса а и b, легко осуществить следующим образом (фиг. 2). На подвижной тележке W, имеющей возможность перемещаться по направляющим АВ и CD только вдоль оси Y, устроен шарнирный параллелограм P1P2Q1Q2. Стержни Р1Р2 и Q1Q2, образующие две стороны этого параллелограма, прикреплены к стержням O1R1 и O2K2 при помощи шарниров в точках Р1Р2, Q1 и Q2, причем так, что расстояния O1P1=O2P2=b и O1Q1=O2Q2=а. При вращении стержней O1R1 и O2R2 вокруг центров O1O2, стержни Р1Р2 и Q1Q2 будут перемещаться параллельно самим себе, и каждая точка (например, K1) стержня Р1Р2 опишет окружность радиуса b, а каждая соответствующая точка K2 стержня Q1Q2 - концентрическую окружность радиуса а. Для осуществления возможности вращения эллипсографа на 360° и более стержни O1R1 и O2R2 должны быть выполнены коленчатыми; тогда стержни Р1Р2 и Q1Q2 смогут перемещаться в горизонтальных параллельных плоскостях, не задевая друг друга. В точке K1 перпендикулярно к стержню Р1Р2 неподвижно закреплен стержень K1F, двигающийся вместе со стержнем Р1Р2 в плоскости его перемещения параллельно самому себе. Если вращать эллипсограф, оставляя тележку неподвижной, то точка М пересечения стержней K1F и Q1Q2 опишет эллипс
х = a cos t
y = b sin t.
Чтобы получить из эллипса проекцию осевой линии свитой в спираль проволоки, необходимо во время вращения эллипсографа перемещать тележку на расстояние ct. Для регулировки этого расстояния служит проволока, намотанная на барабан, который вращается вместе со стержнем O1R1 вокруг оси О1 и имеет радиус, равный 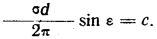 Конец проволоки сходит с барабана строго параллельно оси Y и закреплен в неподвижной точке Н. Так как тележка перемещается в направлении оси Y, а закрепленный конец проволоки стремится воспрепятствовать этому перемещению, то проволока будет сматываться с барабана и, сматываясь, приведет барабан во вращение, а вместе с ним и эллипсограф. Так как радиус барабана равен величине с, то при повороте его на угол t длина сошедшей с него проволоки будет равна ct. На это расстояние передвинется и тележка, увеличив ординату эллипса на величину ct. Следовательно, точка М, имеющая абсциссу х = a cos t (общую для эллипса и проекции осевой линии проволоки), будет иметь уже не. ординату эллипса y = b sin t, а ординату проекции осевой линии проволоки у = b sin t + ct. Таким образом, если бы в точку М был помещен чертежный карандаш, то он вычертил бы на неподвижной плоскости уже не эллипс, а проекцию осевой линии проволоки, но помещать в точку М карандаш нельзя, ибо его перемещению, будут мешать стержни Р1Р2 и Q1Q2; к тому же площадь под эллипсографом, где должна быть помещена чертежная доска, занята тележкой. Поэтому приходится помещать чертежный карандаш не в точке М, а в точке M1, взятой на трубке ММ1, являющейся продолжением стержня K1F, в которой он может(свободно перемещаться а продольном направлении. В точке М эта трубка, Т-образно скреплена со второй трубкой, которая может перемещаться вдоль стержня Q1Q2. Так как точка М описывает проекцию осевой линии свитой в спираль проволоки, то и точка M1 также будет описывать эту же проекцию, но на расстоянии ММ1=1 от первой проекции. В самом деле, в каждый, момент ордината точки M1 равна ординате точки М, а абсцисса точки М1 равна абсциссе М плюс отрезок 1.
Конец проволоки сходит с барабана строго параллельно оси Y и закреплен в неподвижной точке Н. Так как тележка перемещается в направлении оси Y, а закрепленный конец проволоки стремится воспрепятствовать этому перемещению, то проволока будет сматываться с барабана и, сматываясь, приведет барабан во вращение, а вместе с ним и эллипсограф. Так как радиус барабана равен величине с, то при повороте его на угол t длина сошедшей с него проволоки будет равна ct. На это расстояние передвинется и тележка, увеличив ординату эллипса на величину ct. Следовательно, точка М, имеющая абсциссу х = a cos t (общую для эллипса и проекции осевой линии проволоки), будет иметь уже не. ординату эллипса y = b sin t, а ординату проекции осевой линии проволоки у = b sin t + ct. Таким образом, если бы в точку М был помещен чертежный карандаш, то он вычертил бы на неподвижной плоскости уже не эллипс, а проекцию осевой линии проволоки, но помещать в точку М карандаш нельзя, ибо его перемещению, будут мешать стержни Р1Р2 и Q1Q2; к тому же площадь под эллипсографом, где должна быть помещена чертежная доска, занята тележкой. Поэтому приходится помещать чертежный карандаш не в точке М, а в точке M1, взятой на трубке ММ1, являющейся продолжением стержня K1F, в которой он может(свободно перемещаться а продольном направлении. В точке М эта трубка, Т-образно скреплена со второй трубкой, которая может перемещаться вдоль стержня Q1Q2. Так как точка М описывает проекцию осевой линии свитой в спираль проволоки, то и точка M1 также будет описывать эту же проекцию, но на расстоянии ММ1=1 от первой проекции. В самом деле, в каждый, момент ордината точки M1 равна ординате точки М, а абсцисса точки М1 равна абсциссе М плюс отрезок 1.
Для построения проекции поверхности спирали необходимо добавить к эллипсографу приспособление, дающее направление нормали к проекции осевой линии проволоки. Его легко получить, если к параллелограму P1P2 Q1Q2 добавить параллелограм Q1Q2R1R2. Стержень R1R2 этого параллелограма прикреплен шарнирами в точках R1 и R2 к коленчатым стержням O1R1 и O2R2, так что O1R1=O2R2=а+b=ρ. Этот стержень может перемещаться в горизонтальной плоскости, параллельной плоскостям перемещения стержней Р1Р2 и Q1Q2. Вокруг точки М1, как центра, может вращаться стержень N1N2, оканчивающийся вилкой Z. Вилка охватывает направляющий штифт Е, укрепленной на стержне Kg на расстоянии KE=1+c от стержня R1R2, с которым стержень Kg скреплен неподвижно под прямым углом (в плоскости его перемещения). Точка М1, описывающая проекцию осевой линии спирали, и точка Е дают стержню N1N2 время вращения эллипсографа всегда направление нормали к проекции осевой линии проволоки, ибо
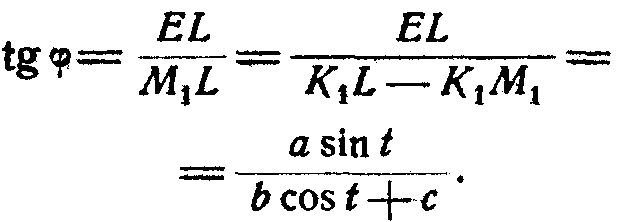
Чертежные карандаши, укрепленные в точках N1 к N2 на некотором расстоянии от точки М1, опишут огибающую, которая и будет являться проекцией поверхности спирали на плоскость.
Преимущество настоящего прибора по сравнению с уже известными, по данным автора, заключается в том, что он вычерчивает проекцию поверхности спирали, как огибающую (непосредственно в виде двух линий), а вышеуказанные уже известные приборы дают возможность вычерчивать лишь семейство окружностей, а не их огибающую, что значительно затемняет чертеж.
| название | год | авторы | номер документа |
|---|---|---|---|
| Прибор для вычерчивания поверхности биспирали | 1937 |
|
SU56101A1 |
| Прибор для вычерчивания эллипсов | 1973 |
|
SU454139A1 |
| ЭЛЛИПСОГРАФ | 2000 |
|
RU2193491C2 |
| Грузонесущий кабель | 1978 |
|
SU942166A1 |
| ПРОСТРАНСТВЕННАЯ СЕТЬ | 2012 |
|
RU2476631C1 |
| Эллипсограф | 1984 |
|
SU1158386A1 |
| ВИБРОИЗОЛЯТОР С БОЛЬШИМ ХОДОМ И СПОСОБ ИЗГОТОВЛЕНИЯ ЕГО УПРУГОГИСТЕРЕЗИСНЫХ ЭЛЕМЕНТОВ | 2012 |
|
RU2520230C2 |
| Передаточный механизм | 1983 |
|
SU1209042A3 |
| ФИЛЬТР ДЛЯ ЗАКАЧКИ ВОДЫ В СКВАЖИНЫ | 2014 |
|
RU2567307C1 |
| УСТРОЙСТВО ДЛЯ ПРЕДОТВРАЩЕНИЯ ПОСАДКИ ПТИЦ НА ТРАВЕРСЫ ОПОР ВОЗДУШНЫХ ЛИНИЙ ЭЛЕКТРОПЕРЕДАЧИ И ПЕРИМЕТРЫ КРЫШ ЗДАНИЙ (ВАРИАНТЫ) | 2015 |
|
RU2603838C1 |
1. Прибор для вычерчивания проекции поверхности спирали с применением эллипсографа, установленного на подвижной вдоль чертежной плоскости каретке, отличающийся тем, что, с целью вычерчивания проекций поверхности спирали, как двух огибающих семейства окружностей, с центрами, лежащими на проекции осевой линии спирали, эллипсограф выполнен в виде шарнирного параллелограма Р1Р2 Q1Q2, поворотного вокруг концов O1 и О2 стержней O1R1 и O2R2 и снабженного прикрепленным к стержню Р1Р2 перпендикулярным стержнем K1F, пропущенным в подвижной вдоль стороны Q1Q2 трубчатый стержень ММ1, несущий пишущие органы, вычерчивающие при перемещении каретки W вдоль чертежной плоскости проекцию поверхности спирали.
2. Форма выполнения прибора по п. 1, отличающаяся тем, что, с целью установки пишущих органов на линии, нормальной к проекции осевой линия спирали, стержни O1R1 и O2R2 шарнирно соединены со стержнем R1R2, жестко скрепленным с перпендикулярным к нему стержнем Kg с пальцем Е, входящим в вилку Z поворотного вокруг точки M1 стержня ММ1 рычага N1N2, несущего пишущие органы.
3. Форма выполнения прибора по пп. 1 и 2, отличающаяся тем, что для возможности вращения параллелограмов P1R1 P2R2 и P1Q1 Q2P2 вокруг концов O1 и O2 стержней O1R1 и O2R2 на 360° стержни O1R1 и O2R2 выполнены коленчатыми.
Авторы
Даты
1939-11-30—Публикация
1937-10-19—Подача