На современных американских самолётах, предназначенных для дальних полётов, обычно устанавливаются купола для астрономических наблюдений, стандартного образца, имеющие форму шарового сегмента. Эти купола изготавливаются обычно из подогретых листов, плексигласа, на две стороны которых создаётся разность атмосферного давления, вследствие чего плексиглас выдавливается в сторону меньшего давления, принимая лри этом сферическую форму.
Такой слособ изготовления сфе-рических куполов приводит к тому, что толшина их стенок получается не одинаковой: у основания купола больше, у вершины - мень.ше, вследствие чего внутренняя и ;внешняя поверхности купола становятся неконцентрическими. Луч света, проходящий сквозь такой купол, претерпевает рефракцию, т. е. отклоняется от своего первоначального направления, по двум причинам: во-первых, от несовпадения направления луча с радиусом поверхности купола и, во-вторых, из-за неконцентричности внешней -И внутренней поверхностей купола.
Угол рефракционного отклонения луча может изменяться в значительных пределах; от нескольких минут дуги по полуградуса и больше. При этом он зависит как ог высоты наблюдаемого светила, так и, ещё в большей степени, от положения секстанта относительно . Последнее обстоятельство заставляет при применении сферических куполов пользоваться подвесными секстантами, производя после их подвески исследование куполов на рефракцию в зависимости от изменения высоты светил.
Если в распоряжении штурмана имеется только ручной секстант, измерение высот светил делается для него крайне затруднительным, так как, держа секстант в руках, невозможно гарантировать стандартное его положение относительно купола. При нестандартном же положении секстанта величина ошибки измерения, происходящая из-за незнания точного значения рефракции купола, может значительно превышать случайные ошибки измерений высот светил в воздухе. Предлагаемый купол для астрономических наблюдений из
штурманских кабин, например, самолётов, имеет ту особенность, что он имеет коническую форму, в результате чего уменьшается величина ошибки астрономических наблюдений, возникаюш,ей вследствие рефракции лучей при прохождении сквозь стенки купола.
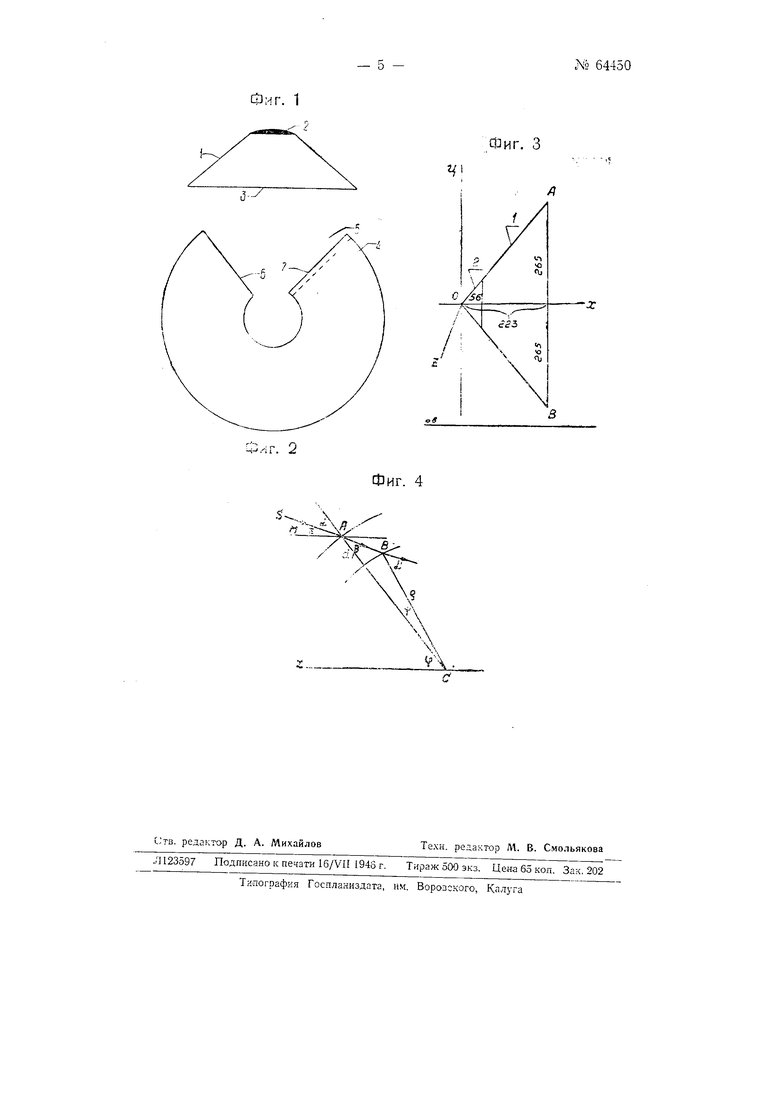
На чертеже фиг. 1 изображает продольный разрез примерной формы выполпения купола, фиг. 2 - вид в плане заготовки купола, а фиг. 3-4 поясняют влияние купола конической формы на результаты астрономических наблюдений.
Купол состоит из двух частей: усечённого конуса 1 из плексигласа и металлического колпака 2.
Угол между образующей конуса и плоскостью основания 3-около 40°. Плексиглас, из которого изготовлен конус 1 купола, должен обладать высокой прозрачностью и зеркальностью. Толщина плексигласа около 5-6 мм.
Для изготовления конуса из листа плексигласа делается заготовка 4 формы, показанной на фиг. 2. Коническая форма заготовке 4 придаётся после её подогревания на деревянном шаблоне. Края 6-7 выреза 5 или склеиваются вдоль об разующей конуса („на стык или „на клин), или заклёпываются.
Колпак 2 купола 1 изготавливается из лёгкого металла. Он наглухо прикрепляется к верхней части конуса и имеет хорошо обтек.аемую форму.
При установке купола на крыше фюзеляжа штурман может измерять высоты дневных и ночных светил в пределах от 45 до 80, т. е. в тех же пределах, что и при применении сферического купола.
При измерении высот светил в центральной плоскости купола (т. е. в плоскости, проходящей через ось конуса) рефракция купола равна нулю. При небольшом отклонении от центральной плоскости поправка на рефракцию принимает отрицательное значение, но она практически настолько мала, что ею можно пренебречь.
При пересечении поверхности конуса 1 плоскостью, проходящей через ось ОХ конуса, получаются две перес2кающиеся в вершине конуса прямые ОА и ОВ (фиг. 3). Отсюда следует, что при наблюдении светил в центральных плоскостях конуса рефракция отсутствует.
Пересечём конус плоскостью, параллельной оси конуса и отстоящей от оси на расстоянии К см. Как известно, в этом случае в плоскости сечения получится гипербола, большая ось которой параллельна оси конуса.
Для получения уравнения этой гиперболы выберем прямоугольную систему координат так, как это показано на фиг. 3 (ось ОХ идёт вдоль оси конуса) и проведём плоскость, уравнение которой Z К.
Уравнение конуса в прямоугольной системе координат:
Х2уЗji
Ui 5i
В случае кругового конуса , зная же размеры усечённого конуса
А купола нетрудно найти, что
265 , т. е. Ь, 1,19 а,.
В таком случае уравнение конуса примет вид:
1,192
принимая Z K, получаем уравнение гиперболы:
откуда видно, что полуоси гиперболы равны:
тг
а и Ь К.
1Д9
Выведем теперь выражение радиуса кривизны гиперболы в зависимости от координаты X.
Напишем общее выражение радиуса кривизны гиперболы. Подставляя в это выражение значения а и 5, полученные выше, а также, имея в виду, что для гиb / перболы х2 -а2, находим, после ряда преобразований (2,7 х2-0,8 k2 Пользуясь этой формулой нетрудно вычислить значения радиусов кривизны гиперболы для различных значений К и X. Результаты вычислений приведены в таблице 1. Таблица 1
Из рассмотрения этой таблицы видно, что в середине конуса (Х 12 см), а тем более у его основания (X 18 см) радиус кривизны, гиперболы во всех случаях настолько велик, что кривизной гиперболы можно пренебречь, т. е. рассматривать её как прямую. При X 6 см, т. е. непосредственко под колпаком купола (низ которого находится, как это видно из фиг. 3, на расстоянии 56 мм от вершины конуса), радиус кривизны гиперболы значительно меньше, вследствие чего представляется целесообразным определить для этого случая величину рефракции, происходяш,ей от кривизны сечения конуса.
Обозначим через d толщину плексигласа и через Z -зенитное расстояние светила. Пусть ломаная SAB (фиг. 4) изображает путь луча светила с углом падения а, углом отражения (3 и углом выхода я , а точка С обозначает центр кривизны гиперболы в точке падения луча. При этом для простоты выводов предполагается, что центры кривизны внешней и внутренней гиперболы совпадают.
По законам преломления света
sin а
Sin -i -, где п - показатель
преломления плексигласа. Но, как это видно из фиг. 4, а - z, следовательно:
. sin (9 - z)
Для определения угла ;, входящего в правую часть этого выражения, воспользуемся формулой, дающей тангенс угла между нормалью к гиперболе и осью а- У
tg 9 -,
где у и X - текущие координаты гиперболы.
Из уравнения гиперболы легко
У 1 / ь- ьгтолучиты- . -.
предыдущему имеем:
1,19- и b k,
Л.
следовательно,
--lir-F
или
l,414-|t9 0,707 . ,
t3
1Рефракционное отклонение луча пронсходит вниз, т. е. поправка на рефракцню должна быть отрицательной.
2Эта формула написана дляс.пучая, когда jTO.T - отсчитывается по часовой стрелке. Соединим точку С с точками А и В и проведём линии AM и CL, параллельные оси, конуса (т. е.- вертикали). Введём обозначения: АС1 а и ВСА 6. Очевидно, угол 6 показывает, под каким углом сходятся касательные к двум концентрическим окружностям, проведённые в точках А и В. Иначе говоря угол О можно рассматривать, как преломляющий угол призмы (клина), вызывающей рефракцию луча светила Определим этот угол. ,sin i АВ Из А ABG имеем d но А.В откуда следует d sin i is
Принимая X 6 см и придавая зенитному расстоянию наименьшее из встречающихся на практике значений Z 10°, соответствующее максимальному значению угла j, вычисляем угол 1 по формулам 2, 3 и 4 для различных значений К. Результаты вычислений угла о даны в таблице 2.
Таблица 2
Для определения величины рефракционного отклонения воспользуемся формулой призмы:
sin а п. Sin (S -г i),
.здесь а-угол падения луча на призму, р - соответствующий угол :преломления, « - угол выхода луча из призмы, (iJ - преломляющий угол призмы и п - коэфициент преломления.
Рефракционное отклонение по.лучается по формуле: г а - а.
Пользуясь этой формулой, а также формулой sin а и принимая п 1,37, находим значение г, приве,денное в нижней строке таблицы 2.
Из трёх полученных значений г первое: Г - настолько мало, что им можно пренебречь. Таким образом даже при неблагоприятных условиях (X 6 см и Z 10) рефракция купола делается ощутительной только при удалении плоскости наблюдений от центральной плоскости купола на 2 см. Но этот случай очень мало вероятен, так как 2 см составляют почти / радиуса основания колпака купола, и .легко может предохранить себя ог столь заметного отклонения ог центральной плоскости.
С другой стороны, если зенитному расстоянию светила придать ..значение 20° (практически очень peltKo приходится наблюдать светила с меньшими Z) и несколько
увеличить X, приняв его равным 8 см (в этом случае луч от светила проходит сквозь купол приблизительно на 3 см ниже основания колпака), то при К 3 см получается, что 6 11,7 и г .
На основании всего сказанного можно принять, что даже при наиболее неблагоприятных встречающихся на практике условиях наблюдений рефракцией купола практически можно пренебрегать.
Коническая форма купола даёт возможность производить астрономические измерения высот дневных и ночных светил в требуемых на практике пределах (от 15 до 80).
При.применении купола конической формы следует избегать измерения высоты светил в плоскостях, далёких от центральных плоскостей купола и сквозь части купола, располонсенные непосредственно под его колпаком.
Преимущество конического купола перед сферическими куполами состоит в том, что при его применении можно пренебрегать рефракционным смещением, максимальное значение которого практически не превыщает Эго даёт возможность при наличии конического купола пользоваться секстантами любой конструкции, не производя никаких предварительных испытаний купола.
Недостатком конического астрокупола является только- наличие щва, вдоль которого производится склейка или заклёпка плексигласа. Эгот недостаток не имеет, однако, сколько-нибудь существенного значения, так как благодаря шву выпадает из наблюдений область неба шириной не более 3-4°.
Предмет изобретения
Купол для астрономических наблюдений из штурманских кабин, например, самолётов, отличающийся тем, что, с цглью уменьшения величины ошибки астрономических наблюдений, возникающей вследствие рефракции лучей при прохождении сквэзь стенки купола, последний выполнен конической формы.
Фиг. 3
Ч
х
«




Фиг. 4
Авторы
Даты
1945-01-01—Публикация
1943-10-22—Подача