Изобретение относится к обработке резанием, а именно к обработке сквозных
круглых отверстий с наклонными стенками, когда диаметр отверстия значительно пре- его глубину, осуществляемой конус- ными фрезами или кольцевыми сверлами, зубья которых представляют собой кольце вой режущий контур, перемещающийся при вращении инструмента вокруг своей оси и при обращении вокруг оси отверстия по. сферической поверхности.
Целью изобретения является повышение точности обработки отверстия с наклонной образующей за счет выполнения его в форме участка гиперболоида.
Благодаря малой кривизне получаемой тдким образом гиперболической поверхности зта поверхность мало отличается от за- данной конической поверхности отверстия. , Чертеж иллюстрирует нахождение ги- перболической образующей отверстия, прорезаемого предложенным способом.
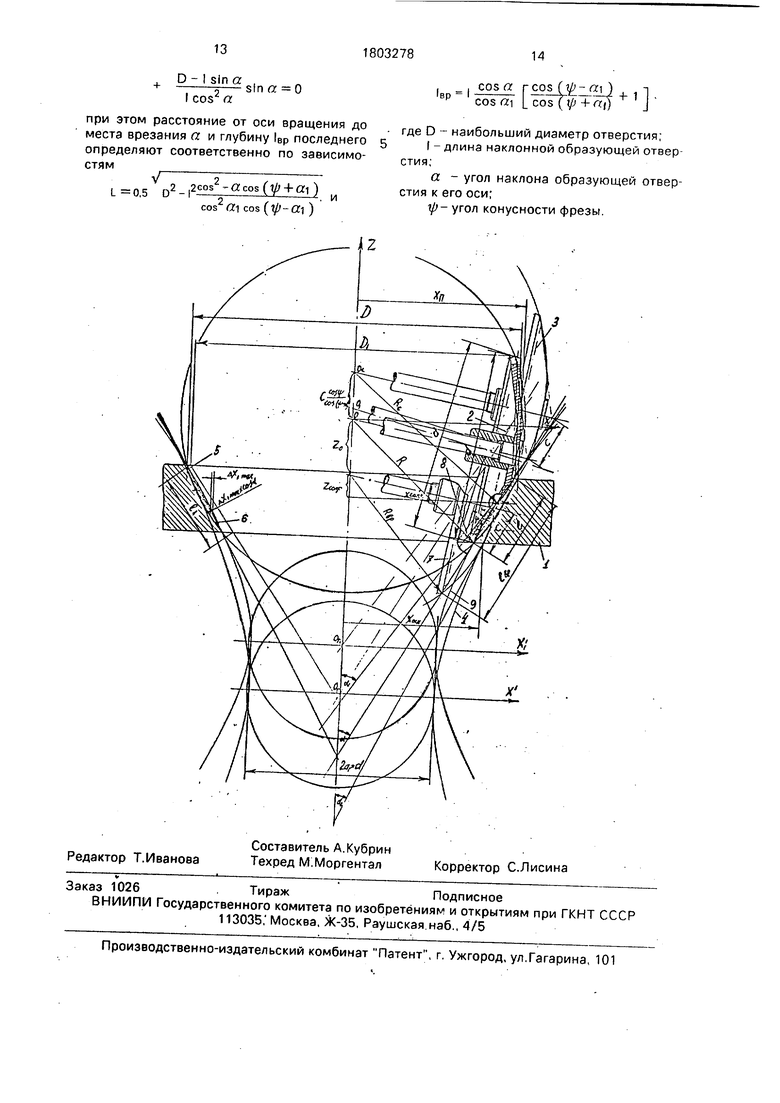
Для определения параметров обработки предложенным способом предварительно следует рассмотреть, какую форму будет иметь отверстие в детали 1 с номинальными размерами: диаметр по верхней поверхности D, конусность стенки а, глубина по на- клонной образующей I/ если его обрабатывать конусной фрезой 2, врезаемой при вращении ее вокруг своей оси по направлению образующей I с одновременным с врезанием обращением вокруг оси отверстия, на расстоянии половины диаметра от центра отверстия. Размеры фрезы 2 назначены из условия, что при погружении на глубину I в деталь 1 при обращении вокруг оси отверстия ее режущий контур будет перемещаться по сфере радиусом в этот моЮ
С
00
о
со го
VI 00
мент, равным R
ЧР-lslrvg)2 +cos2g
2 cos cr гфи отстоянии центра этой сферы (точка 0)
рт поверхности Z0
D sina- I
, что обеспе2 cos ct
чивает наибольшее совпадение усилий резания с направлением движения инструмента вокруг оси отверстия. В этом случае угол конусности фрезы ip и диаметр ее d связаны между собой и размерами отверстия соотношением tg ip -
dV4H2-d2+l2-2H 4 н2 - d2
Н
D-l since
или относительно диаметра
2 cos a
,. d cos (ib + a) фрезы d ---y cosct --
В начальный момент обработки, когда конец конусной фрезы только касается поверхности детали, радиус сферы резания составляет наибольшую величину и равен
RH . V(b Jj.M.0). а центр
2 cos a этой сферы отстоит от поверхности детали
-. D sina + l на расстоянии Z0n -9 .
L С/wo CЈ
По мере погружения фрезы в деталь по направлению образующей с одновременным обращением вокруг оси отверстия центр сферы резания, перемещающийся по этой оси, опускается, а радиус сферы уменьшается. В конце концов при пересечении центра режущего контура (представляющего круг, соединяющий концы зубьев фрезы) с осью отверстия диаметр сферы резания уменьшится до диаметра фрезы d, а при врезании фрезы дальше будет снова увеличиваться.
За каждый оборот инструмента вокруг оси отверстия стенка отверстия формируется дуговыми подрезами из пересекающихся или последовательно подрезаемых дуг.
Математически форму стенки отверстия может характеризовать огибающая линия, проходящая по вершинам пересекающихся дуг. Для определения характера этой линии зададим смещение фрезы по образующей I на величину С в сторону, противоположную врезанию., - на чертеже положение фрезы 3. Вследствие такого перемещения инструмента центр переменной сферы резания О переместится в точку Ос на величину, рав- cosyj
ную С
вдоль оси отверстия.
cos () В координатах XOZ
сферы резания равен vx 2 -f г/ R, а радиус сферы резания при смещении фрезы на
эадиус переменной
CV 2+tZ-Cc V Как видно на чертеже, квадрат радиуса сферы резания при смещении в зависимо
сти от величины смещения С и параметров отверстия равен
, Яе -1§-,.
+ Z0 + 0 - С) cos .
Таким образом, уравнение изменяющего гося радиуса сферы резания в зависимости от трех переменных, и С будет иметь вид
15
+ P-c5s V- Tlllne-
+ С sin a)2 + {Z0 + I cos a +
+ С cos a COSJ/
--rlr
al
(1)
co$(ip-ay
Для получения уравнения огибающей возьмем производную от (1) по С и, приравняв ее нулю, определим С в зависимости от X, Z и заданных параметров отверстия и фрезы, а затем, подставив полученное зна- чение в (1) и преобразовав, получим уравнение огибающей линии,
x2+-z230
J Dcost/Hsln(yj+O)3slna+2zcQS a costal2 J A cos2 a cos (i/ ) cos (t/ + «)
35
D2 - 2 D I sin a +12 4 cos2 a
(2)
Эта линия является кривой второго порядка. Анализ этой кривой, произведенный при выражении ее уравнения в общем виде, показывает, что ее конкретный вид определяет соотношение costy и sin а. Если cos .ty sin а, то кривая представляет собой
гиперболу, как это показано на чертеже - 4, где показано осевое сечение отверстия. Следовательно, само отверстие будет иметь форму участка однополостного гиперболоида.
Если же cost/ sina, т.е. 1р а, то каждая последующая сфера резания будет полностью подрезать предыдущую. В этом случае при любом значении X и Z будет иметь место круг - образующая стенки отверстия будет круговой, а сама стенка будет иметь сферическую форму. Значит при использовании кольцевого сверла fy 90°) cos ty 0 sina, ртенка отверстия всегда будет
сферической, что, как сказано выше, и имеет место в способе-прототипе. Таким образом
для решения поставленной задачи представляет интерес только получение гиперболической формы стенки отверстия.
Каноническое уравнение гиперболы, когда начало координат расположено в ее центре
определяется уравнением действительная полуось
D sin V + lcos (y + 2 cos a
аг
луось
Ьг
поверхности детали центр гиперболы отстоит на величину Zn ZCM - Zo D cos (тр- a)- cos г/j cos (V + a)
sin 2 a
Поверхность гиперболического отверстия, образованного при врезании конусной фрезы с углом конусности чр, меньшим, чем угол наклона образующей а к оси отверстия, по направлению этой образующей нигде не совпадает с заданным отверстием в форме усеченного конуса. Абсцисса образуемого в гиперболоиде на поверхности отверстия (при Z -Z0 в уравнении (2)) равна





| название | год | авторы | номер документа |
|---|---|---|---|
| Способ обработки отверстий с наклонной образующей | 1991 |
|
SU1836998A1 |
| Способ обработки отверстий с наклонной образующей | 1991 |
|
SU1836999A1 |
| СПОСОБ ОБРАБОТКИ ОТВЕРСТИЙ С НАКЛОННОЙ ОБРАЗУЮЩЕЙ | 1991 |
|
RU2016712C1 |
| Способ обработки сквозных конических отверстий кольцевым инструментом | 1989 |
|
SU1741977A1 |
| Способ вырезки сквозных цилиндрических отверстий | 1988 |
|
SU1634389A1 |
| Способ получения корней стружки | 1989 |
|
SU1699720A1 |
| Способ бесцентрового шлифования шариков | 1989 |
|
SU1742040A1 |
| Способ обработки конических отверстий | 1982 |
|
SU1074663A1 |
| Устройство для крепления режущего инструмента | 1991 |
|
SU1808522A1 |
| Вибросверлильное устройство | 1988 |
|
SU1690966A1 |

.D sin ( cos(V)cos(y)cos(V;+rz) sin 2 а
Как указывалось, диаметр переменной сферы резания по мере врезания фрезы по образующей уменьшается,до величины диаметра фрезы, а затем снова увеличивается, т.е. диаметр горловины получаемого гиперболоида равен диаметру примененной конусной фрезы d 2аг.
Наклон асимптоты гиперболы осевого сеч ения отверстия к оси - оси отверстия рав|ен
. . -т...
cos ( у - « ) cos (f/ + a ) угол наклона асимптоты гипербйлы не равен углу наклона образующей номинального фонического отверстия, Смещение начала кооЬдинат по оси Z из центра О в центр Ог определяется как
D costy- I sin ()cos
-CM
а от
sin 2 а
I , cos (у - a) slna I sin ( x z 2 cos (i)+a} Г 2 cos a
/
sin cos ун sln( cost/JcosaZ
----2 cos a cos (tp-a} ---При врезании инструмента только на глубину отверстия по образующей поверхность отверстия в верхней части будет иметь гиперболическую форму 5. а в нижней
- сферическую б с радиусом сферы R. Линия сопряжения этих поверхностей отстоит от поверхности детали на величину, равную
- lcos(ti -fa)
Ј.Ј--L ----1-J---i
-conp.
2 cos a
полученную решени2 D2
ем системы двух уравнений: (2) и X + Z - R .
При движении фрезы по образующей дальще с выходом ее конца с противоположной стороны отверстия будет продолжаться формирование гиперболической поверх- ностф стенки уже в нижней части отверстия.
Глубину погружения инструмента 7 для о&работки по форме гиперболоида всего от
ХП
0,5 Т)2 +I
,2 cos (tp + а) cos (f)-a}
а по основанию (при Z -(Z0 + I cos a)
XOCH
(3)
0.5 (D-2 I sin а)2 -H2
cos ( V - a cos (V + tf
(4)
тогда как абсциссы прямой образующей номинального конического отверстия в этих местах соответственно равны 0.5D и 0,5 (D - 2 I sin a).
Формирование гиперболической поверхности отверстия, определяемой огибающей (2), в каждой точке производится при погружении конусной фрезы 2, 3 по образующей на глубину, которая определяется зависимостью, полученной из выражения (1) его решением относительно С. В полученном выражении вместо С - IX,Z.
2,4 cos pH-oOfD2 - D I sin a + I2 X2 -л
cos (y-a)4 cos a
(5)
ве.рстия можно определить, если в уравнение (5) вместо X и Z подставить координаты кромки отверстия Х0сн и определенное по формуле (4) Z -(Zo + I cosa). Полученная в этом случае длина выхода инструмента из- под нижней поверхности детали равна 0сн
. cos()с н 2cos(+g) а глубина его погРУже- - ния от поверхности определяется как
I |Г COS(-Q:) . (V + «)
(6).
Если соединить прямой линией точки Хп и Хосн, то станет ясно, что существует такая гипербола, для которой отрезок I является
аналогичным отрезку ХпХосн. через концы которого также может проходить гипербола и, тогда соответственно должна существовать какая-то образующая Н, при вреззнии по направлению которой конусная фреза будет обрабатывать поверхность гиперболоида, пересекающую поверхность детали по окружностям с радиусами, равными 0,5 D и 0,5 (О - 21 slna). Место отстояния этой образующей от центра отверстия по поверхности детали, обозначенное 0,5 DI, должно быть меньше, чем 0,5 D, а ее наклон относительно оси отверстия под углом ai должен быть больше, чем наклон образующей под углом а. Положение образующей Ь и ее наклон под углом а и определяют направление врезания конусной фрезы при обработке предложенным способом. Определение необходимых данных для его осуществления производится следующим образом.
Если в уравнения (3) и (4) вместо Хп и Хосн подставить 0,5 D и 0,5 (D - 2 I sin а), то в правых частях этих уравнений вместо D, а, и I должны быть Di, ai и И. Кроме того в связи с неизменностью толщины детали I
,, , cos a
cos a И cos ai, откуда и I .
. . QOo СЛ
Таким образом для получения исходных- данных для обработки отверстий с указанной гиперболической поверхностью необходимо решить систему трех уравнений с тремя неизвестными И, Di и ai.
I icos a
cos en
,2Јos() D -DT-fnco ai
о-2,з,па)2(о1-2и.з.па1)2+
W)
. п Хот
tgCQ-ГЕБ ГVD -H2cos(t/ 4-aTV(P-2 I sinoQ2 -H2cos (tft-a) cos() cos (ift+ a)
2, cos a -После определения нового значения уг- 40 ла наклона образующей врезания инструмента следует определить новое расстояние места врезания инструмента в поверхность детали от оби отверстия по на правлению новой образующей.45
,a,vD2 -асоз(tft-bai) 2cos2aicos(V-ai) -
Для получения значений указанных неизвестных в зависимости от параметров обработки нужно из первых двух уравнений системы (7) последовательно подставить значения li и DI в третье уравнение благодаря чему получается уравнение с одним неизвестным относительно tg a
tgaip9 1 9 0 - - L 1 -tg tfttS «1
( D s2 (1 -Hg2 ai ) (1-tg tg «1 , , Ч cos a;1-ftgi/ tgai J
20
D-1 slna I cos2 a
slna 0
(8)
Уравнение (8) в общем виде является уравнением восьмой степени относительно 25 tg см. Нахождение одного требуемого корня может быть осуществлено методом последовательного подбора, например с помощью ЭВМ.
30 Ориентиром для начала подбора мо; жет служить приблизительная симметрия прямой, проведенной через точки Хп и Хосн, с одной стороны относительно образующей I, а с другой - новой образующей
35 Н. В. таком случае начальным значением для подбора угла ai следует брать угол, равныйомприбл. 2а-О2, гдеО2, как видно на чертеже, определяется из выражения
Соответственно изменится и глубина врезания инструмента по новой образующей ai, при которой вся поверхность отверстия обрабатывается по заданной форме гиперболоида. Эта глубина равна
вр;
cos a r cos() . . т cos ai Lcos(V + ai) J
(Ю)
,5Q
. .Обработка отверстия предложенным способом производится той же конусной фрезой, размеры которой: диаметр и угол
конусности определены по приведенным выше формулам. Изменены лишь место и угол врезания 8. Получаемый при такой обработке новый гиперболоид 9 пересекает верхнюю и нижнюю поверхности детали на расстоянии 0,5 D и 0,5 (D - 2 I sin а) от оси отверстия, а его центр Ом, в связи с тем, что ai а, находится выше на оси Z, чем Or. Поэтому кривизна гиперболы 4 в месте пересечения ее детали 1 больше кривизны гиперболы 4 в месте пересечения ее этой деталью.
Критерием оценки требуемой точности размеров полученного отверстия является максимальная величина отключения размеров отверстия как по радиусу, ДХтах, так и пЈ нормали к конической поверхности отверстия. Эта величина может быть определена как максимум разности радиусов гиперболического и конического отверстий, ДХ Хк - ХГ1, где Хк - абсцисса образующей конического отверстия, а Хм - гиперболического, /
ХГ1 определяется из канонического уравнения новой гиперболы, отличающегося от приведенного ранее значением мни- мфй оси в функции от ai (а не от и), а Хк определяется из уравнения прямой образующей в координатах относительно цен-- новой гиперболы.
Общее уравнение величины отклонения получаемого значения радиуса отверстия от номинального значения в зависимости от заданных и новых параметров выражается как
Zn.max - -я- tg П
аг г .cos Oh tg ty sinai cos(V-«i)
В качестве конкретного примера использования предлагаемого способа рассматривается прорезание отверстия, имеющего следующие размеры:
Диаметр по поверхности D 300 мм Угол наклона стенки к оси « 30° Глубина по образующей I 70 мм Назначим угол конусности примененной фрезы равным 20°, тогда ее диаметр в зависимости от этого угла и размеров отверстия будет равен d - 170,43 мм.
Предварительно рассмотрим какие отклонения получатся при обработке отверстия не предлагаемым способом, а при врезании инструмента на расстоянии 0,5 D от центра отверстия по направлению обра- зук}щей и на глубину.
+ Z2slnai
cos()cos()
г -, , rD / D ar sin t/. tga n i (-2---t5w)
(11)
Определение максимального отклонения по радиусу производится подстановкой
в уравнение (11) значения Zmax, полученного
из выражения приравненной к нулю производной от (11) по Z.
Максимальное отклонение - уменьше- ние радиуса обрабатываемого отверстия равно
ДХяах 0.5(D-D1)- sin2 «1-cos (V-ОГ1 )cos (V + o:i )tg2« +
fsln tgCrj
(12)
Из формулы (12) вытекает, что чем меньше угол конусности фрезы 1р, тем меньше отклонение размеров гиперболического отверстия от номинального конического, т.е. тем выше точность обработки. Практический интерес представляет также и расположение плоскости максимального уменьшения диаметра получаемого отверстия, но не в координатах центра гиперболы (Zmax),, а от поверхности отвер- стия. Эта величина может быть определена по формуле
cos (V -gi )cos (ip + a- )tg«-i sin 2 ai - cos (p- a ) cos (V + «1) tg2 a
По формуле (3) радиус отверстия на поверхности детали в данном случае получается равным Хп 152,642 мм. Отклонение по радиусу в большую сторону: ЛЯП Хп - 0,50, Rn 2,642 мм.
Наибольшее отклонение в данном случае должно быть в месте сопряжения верхнего гиперболического участка стенки отверстия с нижним сферическим. Этот участок располагается от поверхности детали на расстоянии Zconp 23,942 мм. Абсцисса места сопряже50
НИЯ Хсопр - R - (Zo+ ZConp) , Хсопр
140,416 мм. Абсцисса номинального радиуса отверстия конической формы в месте сопряжения при Z -Zconp. Хк.сопр 0.5 D - Zconp tg а. Хк.сопр 136,176 мм.
Отклонение размера отверстия по радиусу в месте сопряжения ДЯсопр ХСопр -Хк.сопр ДЯсопр + 4,240-мм.
Таким образом врезание конусной фрезы по образующей на расстоянии радиуса от оси отверстия приводит к существенным отклонениям от заданных размеров в сторону увеличения заданного диаметра отверстия, практически не поддающемуся исправлению.
Теперь рассмотрим какие отклонения будут иметь место при обработке отверстия того же размера предложенным способом. Методом последовательного приближения по формуле (8) определим значение tg «1. Оно составляет 0,7080, а угол «1 35°18.
По формуле (9) вычислим новое расстояние от центра отверстия до места врезания инструмента в поверхность детали по образующей, наклоненной относительно оси отверстия на угол «1. Это расстояние равно 147,264мм.
Глубина, врезания фрезы по образующей И для полной обработки гиперболической стенки отверстия должна быть не менее определенной по формуле (10), IBP 137,230 мм. При этом следует предварительно прорезать отверстие на глубину И, которая для рассматриваемого примера равна И 74,230 мм, а затем, после удаления вырезанного таким образом сердечника, дальнейшим продвижением вращающейся фрезы по образующей с одновременным ее обращением вокруг оси отверстия, довести инструмент до глубины lep по образующей..
По формуле (12) определяется максимальное отклонение по радиусу размера гиперболического отверстия от номинального конического. Величина этого отклонения раёна АХтах -1.649 мм. По нормали к поверхности конического отверстия величина отклонения составляет AXmax cos a 1,649 х cos 30° 1,428мм.
Для уменьшения величины отклонения размеров гиперболического отверстия от размеров конического уменьшим угол конусности фрезы с 20° до 15° и соответственно зависимый от этого угла диаметр фрезы уменьшится до величины d 14.6,809 мм.
По формуле (8) новое значение tg «1 при V 15° будет tg ai 0,6696, а ai 33°48 . Новое отстояние места врезания фрезы
от центра отверстия L ,899 мм, а ее
полная глубина врезания - Ц 125,491 мм.
Новое значение максимального отклонения в плоскости, параллельной поверхно- стям детали, равно ДХтах 1,008 мм, а по нормали к поверхности отверстия ДХтах cosa 0,873, т.е. более чем в полтора раза меньше чем при V 20°,
При уменьшении угла а как это видно на чертеже ниже опускается центр гиперболы и поэтому уменьшается ее кривизна в области обрабатываемой детали. Поэтому для повышения точности размера вырезаемых отверстий следует применять фрезы с 5 возможно меньшим углом конусности. Минимально-допустимый диаметр фрезы в этом случае равен d 2 cos V d вала, где deana диаметр вала, на котором укреплена фреза.
0 Таким образом, посредством только незначительного изменения параметров обработки по углу, месту и глубине врезания инструмента - конусной фрезы обеспечивается повышение точности обработки отвер- 5 стий с наклонными стенками. При этом также обеспечивается достаточно высокое качество поверхности отверстий и используются более дешевые чем кольцевые свёрла, конусные фрезы с малыми1 углами 0 конусности и диаметром меньше чем у кольцевых сверл.
Формула изобретен и я Способ обработки отверстий с наклонной образующей, при котором инструмент 5 устанавливают под углом к оси отверстия, сообщают ему вращение вокруг своей оси и круговое перемещение вокруг оси отверстия с одновременным врезанием в деталь в направлении, совпадающем с образую- 0 щей инструмента, при этом расстояние от оси отверстия до места врезания инструмента выбирают меньшим радиуса отверстия, а глубину врезания - большей глубины отверстия, отличающийся тем, что, с 5 целью повышения точности обработки отверстия за счет выполнения его в форме участка гиперболоида, для обработки берут инструмент в виде конусной фрезы с углом конусности, меньшим угла наклона образу- 0 ющей отверстия к его оси, а врезание осуществляют под углом а к оси отверстия, который определяют из выражения
55
tgaiF V +tg - I 1 -ta2t/ tazcti
V
( D f ( 1 +tg2 «1) ( 1-tg Vtg ai . + v I cos a 14-tg V tg «1 J
D - I sin a I cos2 a.
sin a 0
при этом расстояние от оси вращения до . где D - наибольший диаметр отверстия; места врезания а и глубину 1вр последнего 5I - длина наклонной образующей отвер- определяют соответственно по зависимостям
L 0/D3H2 Vacos + g1) и
cos «1 cos(l/ -«i )
стия;
a - угол наклона образующей отверстия к его оси;
тр- угол конусности фрезы.
, - i C05a + i 1 |BP cos« LcostV+rtf) J
где D - наибольший диаметр отверстия; I - длина наклонной образующей отвер-
стия;
a - угол наклона образующей отверстия к его оси;
тр- угол конусности фрезы.

| Способ обработки конических отверстий | 1982 |
|
SU1074663A1 |
| Прибор для равномерного смешения зерна и одновременного отбирания нескольких одинаковых по объему проб | 1921 |
|
SU23A1 |
| Устройство для видения на расстоянии | 1915 |
|
SU1982A1 |
| . | |||
Авторы
Даты
1993-03-23—Публикация
1990-12-25—Подача