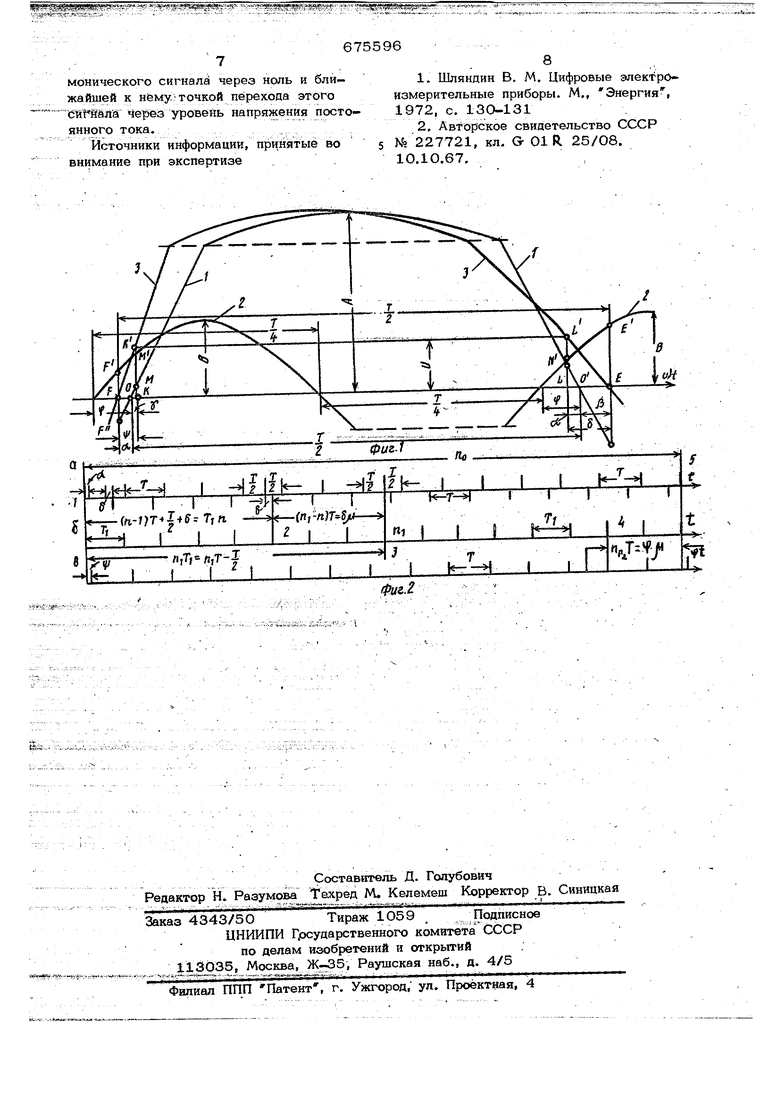
нала через уровень напряжения постоянHoi o тока. Способ осуществляется в два этапа: Этап введения дополнительного време ного интервала и вывод математической зависимости между величиной этого интервала и погрешностями фазового сдвига, обусловленного гармониками; и этап полу 1ения цифровых кодов вспомогательного временного интервала и погрешностей.. - . На фиг, 1 графически изображена по- ловина периода квазигармонического сигнала, первая гармоника (кривая 1) и вторая гармоника /{кривая 2), а кривая 3 - собственная половина периода этого сигнала. На чертежах принйтыследующие обозна чения: величина t периода входных сигнал амплитуда А первой гармоники, амплиту да В второй гармоники, f L фазовый сдвиг f между первой и второй гармониками. Эти обозначения вводятся для получения общих математических зависимостей. Переход квазигармонической кривой 3 в точке Р (О ) от - к + отличает ся от соответствующей точки кривой 1 на угол ct , переход от + к - в точке Е (18О ) отличается на угол . При определении одной из этих величин можно соответственно компенсировать или внести поправку в конечные результаты преобразования фазового сдвига (гдеоС, Y. f погрешности фазы).. Введем вспомогательные временные интервалы: , .jf, О L Б. Точка L соответствует середине периода квазигармонического сигнаJ (ОО 5 fJ первой гармоники представленной на фиг. 2 ). Величина о всегда будет существовать при наличии четных гармоник в основном сигнале. С помощью цифроаналогового преобразования кода величины § получаем соответствующий уровень напряжения постоянного тока U . Суммируем и с квазигармоческим сиг налом и после суммирования по признаку перехода кривой 3 от - к + в точке К получаем второй дополнительный интервал ЕК-Ч(точки К и К по времени идентичны). Далее из графика, приведенного а фиг. 2 , следует p Asin,FF asin2(4-X), Е ftstn г(Т), А sLu., KK KM KAA AsiMj BsmS(f+), LL L N + L, stno 2 (.). Исходя из равенства ординат кривых: 1.И 2.в точках перехода кривой 3 через ноль (Р Р ЕЕ « ЕЕГ а также равенства ординат кривой 3 в точках fj и К , принимая К записываемравенства sinoC Ksin2(4-et), (3) sittjJ Ksin2((4) siny+Kstn() stn,Kstrta(4-U). L Система уравнений (1), (2), (3), (4) и (5) позволяет найти величины с А « Jxu S -Т / «f оИ / Полагая величины и Р известными, с учетом О г i-J можно определить одно из неизвестных. Для того, чтобы ограничиться простыми арифметическими действиями, находим вначале отношение и затем 5(()io(C| или « ) Оля иллюстрации общности полученных результатов сведем решение этой системы к решению системы алгебраических уравнений. Известно, что для углов до 5 величину синуса угла можно заменить величиной угла. После замены уравнения (3), (4), и (5) получат выражения о(кг(ч-.с),(8) ),(9) г(кг(-у)оС-ькагч-), (,о) исключая неизвестное , получим oC()JЗ{l-гк, (и) )Х(1-2К),(12) разделим выражение (11) на выражение (12), получим Из выражения (1) и (2) ot-5 f-4-c{Годставляя йначекия уравнений (14) и(15) в (13), получим (6). Графическое решение системы уравнений с одним из вариантов числовых значений приведено на чертеже. На фиг, 2,6 показана последовательность импульсов с периодом Т (в соответствующем масштабе). Импульсы, при вязанные в точке f , (для наглядности) показаны положительными, импульсы, привязанные в точке Е - отрицательными. На фиг. 2, в дана последовательность импульсов вспомогательного гене ратора (ВГ) с периодом Т (величина T близка к Т). В этом случае периоди чески (точки 1 и 5) происходят совпадения импульсов этих последовательностей. Период состоит из Пр импульсов В При наличии величины будут происходить совпадения в точке 2. Цифровой эквивалент величиныЙ определяется, исхо дя из равенства двух временных интервалов между точками 1,2 и точками 1, 3. Из фиг. 2, а, б следует Сп-1)Т J пТ (16) «.TI п,Т- f (17) из выражений (16) и (17) получим (tt,-tt) (Т-Т,) Умножим обе части выражения (18) на . / --Г, получим («,-П)Т, ;i:JU Из выражения (2 О) следует, что величи на в , умноженная Haju - раз, равна числу (И, - М. ) периодов В Г Т. , где ft - число импульсов ВГ между соседними совпадениями последовательности ВГ с последовател ностью, содержащей 8 ; п - число импульсов определяющих середину п периода Т в Случае идеальной синусоиды (первой гармоники (т. е. О О). Величина П-о находится, как -П. ЕЗеличина ft является цифровым эквив лентом коэффициента умножения /ц и определяется из уравления (19). Таким образом, величина определя ется. как .(ti, . , 5 или в угловых величинах о а/гл О 360 п„ Аналогичным образом относительно точе 1, 4 и 1, 5 выводится зависимость или в угловых величинах Ч 360 Соответственно цифровые эквивалекп, величин (5 и Р равны S ) О « г, , .(24) Как следует из выражений,(23) и (24), числа о и ф выражены в одном коде и поэтому с KisaaWft этих ветгичин мйжно производить действия. Исходя из выражения (7),, можно получить цифровой эквивалент погрешности оС в точке перехода квазигармонического сигнала ; через О . Аналогично находится величи:на ot, для второго канала квааигармони- ческого сигнала. Эти поправки затем :суммируютея с основным преобразованием фазового сдавга между двумя входными сигналами. Кодирование фазового сдвига между двумя сигналами происходит аналогично кодированию угла Ч , т. е. определяется число импульсов ВГ между соседними совпадениями импульсов ВГ с последовательностью импульсов, сформированных на сбойх квазигармонических сигналах. Так как кодирсжание погрешностей и основного фазового сдвига происходит с помощью одного и того же ге- . нератора, то окончательный результат определяем по формс лё r rifr), где ii(, цифровой эквивалент преобразо. . ванкя фазового сдвига; П|,- между Двумя сигналами; Пр- цифровой эквивалент а( первого канала; i- т4-цифровой эквивалент о( второго канала. Формула изобретения Способ преобразования фазового сдвига двух квазигармонйческих сигналов в цифровой Код путем фиксирования точек перехода этих сигналов через ноль и отчета счетных импульсов вспомогательного генератора, отличающий- , я там, что, с целью повышения точноси преобразования фазового сдвига в цифовой код. в каждом канале квазигармрический сигнал суммируют с напряже- ием постоянного тока, уровень которого ропорционален коду временного интервала т середины периода квазигармоническоо сигнала до ближайшей точки перехода того сигнала через ноль, затем в кажом канале кодируют временной интервал ежду второй точкой перехода квазигармонического сигнал через ноль и ближайшей к нему/точкой перехода этого Сйг йапа через ypoiBefib напряжения постоянного тока.
Источники информации, принятые во внимание при экспертизе
675596
8
1. Шляндин В. М, Цифровые электроизмерительные приборы. М,, Энергия, 1972, с. 130-131
, 2. Авторское свидетельство СССР NO 227721, кл. G 01 R 25/08. 10.10.67.


| название | год | авторы | номер документа |
|---|---|---|---|
| Измерительное устройство для геоэлектроразведки | 1980 |
|
SU928288A1 |
| Способ преобразования угла поворота вала фазовращателя в код | 1986 |
|
SU1458973A1 |
| Устройство квазифильтрации гармоник для преобразователей фаза-код | 1973 |
|
SU606208A1 |
| Интегрирующий преобразователь сигналов датчиков переменного тока в код | 1976 |
|
SU764121A1 |
| СПОСОБ ЦИФРОВОГО УПРАВЛЕНИЯ КЛЮЧЕВЫМ ГЕНЕРАТОРНЫМ УСТРОЙСТВОМ УЛЬТРАЗВУКОВОГО ДИАПАЗОНА | 2019 |
|
RU2718003C1 |
| СПОСОБ ВОССТАНОВЛЕНИЯ ИСХОДНЫХ СИГНАЛОВ | 2003 |
|
RU2259591C2 |
| Преобразователь синфазной и квадратурной составляющих основной гармоники переменного тока | 1990 |
|
SU1712893A2 |
| Способ преобразования фазового сдвига в цифровой код | 1982 |
|
SU1101755A1 |
| Преобразователь угла поворота вала в код | 1987 |
|
SU1571758A1 |
| СПОСОБ ФИЛЬТРАЦИИ ИЗМЕРИТЕЛЬНЫХ СИГНАЛОВ | 2003 |
|
RU2251791C2 |


Авторы
Даты
1979-07-25—Публикация
1972-12-01—Подача