Способ восстановления исходных сигналов относится к информационно-измерительной технике и может быть использован для преобразования дискретного сигнала в виде серии равноотстоящих во времени мгновенных значений в непрерывный (аналоговый) исходный сигнал.
Известен способ восстановления непрерывного сигнала по выборке его мгновенных значений (дискретных отсчетов) [Фильтрация измерительных сигналов. Гутников B.C. Энергоатомиздат, Ленинград, 1990, стр.43-45] и реализующее его устройство [Авторское свидетельство СССР № 1562941, МКИ 5 G 06 G 7/30, БИ № 17, 1990], заключающийся в аппроксимации восстанавливаемого сигнала полиномами нулевого порядка путем интегрирования результата перемножения дискретных отсчетов с одиночными прямоугольными импульсами, в результате чего получают ступенчатую кривую.
Существенным недостатком этого способа является большая погрешность, обусловленная значительным уровнем высших гармоник в спектре ступенчатой кривой, причиной появления которых является дискретизация исходных непрерывных сигналов. Для уменьшения уровня погрешности до 1% частота дискретизации должна в десятки - сотни раз превышать значение высшей частоты в спектре исходного непрерывного сигнала, а так как элементы электронной техники (усилители, генераторы, переключающие устройства и т.д.) имеют высшую частоту функционирования, то дискретизация и восстановление с малой погрешностью дискретизированных сигналов, имеющих широкий спектр, становится невозможным.
Известен способ восстановления непрерывного сигнала по выборке его мгновенных значений (дискретных отсчетов) [Фильтрация измерительных сигналов. Гутников B.C. Энергоатомиздат, Ленинград, 1990, стр.43-45. Авторское свидетельство СССР № 1571766, МКИ 5 Н 03 М 3/02, БИ № 22, 1990], заключающийся в аппроксимации восстанавливаемого сигнала полиномами первого порядка путем интегрирования результата перемножения дискретных отсчетов с одиночными линейно изменяющимися (нарастающими или убывающими) импульсами, в результате чего получают кусочно-линейную кривую.
Существенным недостатком этого способа является значительная погрешность, обусловленная присутствием высших гармоник в спектре кусочно-линейной кривой, причиной появления которых является дискретизация исходных непрерывных сигналов. Для уменьшения уровня погрешности до 1% частота дискретизации должна в 22 раза превышать значение высшей частоты в спектре исходного непрерывного сигнала [Фильтрация измерительных сигналов. Гутников B.C. Энергоатомиздат, Ленинград, 1990, стр.50], а потому дискретизация и восстановление с малой погрешностью дискретизированных сигналов, имеющих в своем составе высокочастотные колебания, становятся невозможным.
Известен способ восстановления непрерывного сигнала с ограниченным спектром (т.е. сигнала, содержащего в своем составе частотный компонент с высшей частотой fв) по выборке его мгновенных значений (дискретных отсчетов) [Радиотехнические цепи и сигналы. Баскаков С.И. М.: Высшая школа, 1988, стр.116-118 (теорема Котельникова)], заключающийся в непрерывном с течением времени t суммировании колебаний, вырабатываемых генераторами базисных функций  , амплитуды которых пропорциональны отсчетным значениям сигнала
, амплитуды которых пропорциональны отсчетным значениям сигнала  взятым через равные промежутки времени
взятым через равные промежутки времени 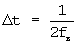 , а их временное запаздывание относительно начала координат пропорционально номеру отсчета К.
, а их временное запаздывание относительно начала координат пропорционально номеру отсчета К.
Однако практически реализовать точное восстановление сигнала с помощью ряда Котельникова невозможно [Фильтрация измерительных сигналов. Гутников B.C. Энергоатомиздат, Ленинград, 1990, стр.49]. Дело в том, что сигнал с ограниченным спектром - это сигнал, длящийся бесконечно долго. При дискретизации такого сигнала будет получено бесконечное число отсчетов 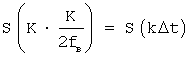 . Для восстановления исходного значения S(t) в произвольный момент времени t нужно учитывать не только все отсчеты, предшествующие этому моменту, но и все последующие отсчеты, т.е. восстановление сигнала по Котельникову возможно только после получения всех отсчетов, что не представляется возможным ввиду неограниченной длительности сигнала.
. Для восстановления исходного значения S(t) в произвольный момент времени t нужно учитывать не только все отсчеты, предшествующие этому моменту, но и все последующие отсчеты, т.е. восстановление сигнала по Котельникову возможно только после получения всех отсчетов, что не представляется возможным ввиду неограниченной длительности сигнала.
Высокоточная реализация этого способа затруднена также отсутствием технических устройств, обеспечивающих точное аналоговое воспроизведение базисных функций 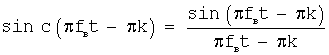 [Матюшин О.Т. Цифроаналоговое формирование радиосигналов. Радиотехника. 1983, № 6, с.9-15].
[Матюшин О.Т. Цифроаналоговое формирование радиосигналов. Радиотехника. 1983, № 6, с.9-15].
Известен способ восстановления исходного сигнала [Радиотехнические цепи и сигналы. Баскаков С.И. М.: Высшая школа, 1988, стр.383], заключающийся в суммировании конечного числа гармонических колебаний кратных частот с амплитудами, пропорциональными модулям коэффициентов дискретного преобразования Фурье (ДПФ), и начальными углами фазового сдвига, равными аргументам этих коэффициентов, число которых равно числу отсчетов N дискретного сигнала.
Существенным недостатком этого способа является необходимость одновременного определения всех отсчетных значений S0, S1, ..., SN-1 исходного сигнала S(t) для определения коэффициентов ДПФ, что ограничивает подлежащие восстановлению сигналы классом периодических или периодизированных сигналов.
Другим существенным недостатком этого способа является необходимость одновременного воспроизведения генераторами гармонических колебаний кратных частот (от колебания основной частоты f0 до колебания с частотой (N-1)f0) и равных амплитуд с одинаковыми начальными углами фазовых сдвигов, что требует ″N-1" системы стабилизации каждого из параметров колебаний (частоты f, амплитуды Um и начального угла фазового сдвига ϕ), а всего 3(N-1) систем стабилизации параметров колебаний, что является сложной проблемой, затрудняющей практическую реализацию.
Этот способ выбран в качестве прототипа.
Таким образом рассмотренные аналоги не обеспечивают решение задачи высокоточного восстановления исходных сигналов по их дискретным отсчетам.
Техническим результатом заявляемого способа является принципиальная возможность высокоточного восстановления исходных сигналов по их дискретным отсчетам.
Задача, на решение которой направлено техническое решение, достигается тем, что в известном способе, заключающемся в суммировании конечного числа гармонических колебаний кратных частот с амплитудами, пропорциональными модулям коэффициентов ДПФ, и начальными углами фазового сдвига, равными аргументам этих коэффициентов, подвергают перемножению каждый из N последовательно поступающих отсчетов дискретного сигнала на задержанные пропорционально номеру отсчета мгновенные значения суммы из  гармонических колебаний кратных частот и равных амплитуд, которую воспроизводят амплитудной модуляцией гармонических колебаний несущей частоты, превышающей в
гармонических колебаний кратных частот и равных амплитуд, которую воспроизводят амплитудной модуляцией гармонических колебаний несущей частоты, превышающей в 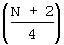 раз частоту повторения восстанавливаемого сигнала, с законом изменения огибающей амплитудно-модулированного колебания, определяемого отношением мгновенных значений синусоидальных колебаний равных амплитуд с кратностью частот, равной половине числа дискретных отсчетов
раз частоту повторения восстанавливаемого сигнала, с законом изменения огибающей амплитудно-модулированного колебания, определяемого отношением мгновенных значений синусоидальных колебаний равных амплитуд с кратностью частот, равной половине числа дискретных отсчетов  .
.
На чертеже показана структурная схема устройства для восстановления исходных сигналов по его дискретным отсчетам.
Здесь: 1 - генератор гармонических колебаний частоты, 2 - формирователь, преобразующий колебания частоты fн в последовательности прямоугольных импульсов той же частоты; 30-3N-1 - масштабные преобразователи на основе операционных усилителей, переключением резисторов в цепях обратных связей которых обеспечивается изменение их коэффициентов передачи K0(t)÷KN-1(t); 4 - коммутатор, управляемый выходными импульсами формирователя 2 и обеспечивающий переключение резисторов масштабных преобразователей 30-3N-1; 50÷5N-1 - амплитудные модуляторы, на модулирующие входы которых подаются управляющие ступенчатые напряжения, изменяющиеся пропорционально соответствующим отсчетам S(kΔ), а на сигнальные входы - амплитудно-модулированные колебания, воспроизводящие запаздывающие на интервалы kΔ относительно начала координат равноамплитудные полиномы; 6 - сумматор, на "k"-е входы которого с выходов всех канальных амплитудных модуляторов непрерывно поступают запаздывающие на "kΔ" равноамплитудные полиномы, амплитуды частотных компонентов которых подвергнуты масштабному преобразованию умножением их на соответствующее номеру канала значение S(kΔ).
Изменение характера преобразований над дискретным сигналом в виде серии равноотстоящих во времени мгновенных значений (дискретных отсчетов) в процессе восстановления исходного сигнала возможно на основе использования базисных функций в виде суммы гармонических колебаний кратных частот и равных амплитуд с кратностью, равной половине числа отсчетов дискретного сигнала.
Действительно, для периодизированного с периодом Т аналогового сигнала S(t) введем конечномерную аппроксимацию в выбранном базисе [Радиотехнические цепи и сигналы. Баскаков С.И. М.: Высшая школа, 1988, стр.381]
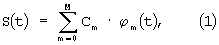
где 
При использовании модели дискретизированного сигнала в виде последовательности дельта-импульсов

где Sk=S(kΔ) - выборочные значения сигнала S(t),
 , a N - полное число отсчетов на периоде Т, ее представление комплексным рядом Фурье
, a N - полное число отсчетов на периоде Т, ее представление комплексным рядом Фурье

с коэффициентами

позволяет при N четном, обеспечивающем сокращение вдвое количества определяемых коэффициентов Сm, получить для процедуры восстановления исходного сигнала следующее выражение
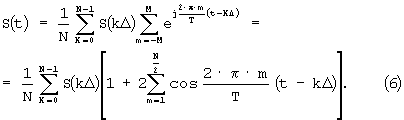
На основании соотношения [Двайт Г.Б. Таблицы интегралов и другие математические формулы. М.: Наука, 1966]

выражение (6) преобразуем к следующему виду:

Из (8) следует, что формирование восстанавливаемого исходного сигнала путем суммирования произведений текущих отсчетных значений S(kΔ) на соответствующие значения запаздывающих равноамплитудных полиномов  возможно в темпе поступления последовательности дискретных отсчетов S(kΔ) без увеличения частоты дискретизации в десятки и сотни раз, как того требуют способы востановления с использованием аппроксимирующих полиномов нулевого порядка (ступенчатая аппроксимация) и первого порядка (кусочно-линейная аппроксимация).
возможно в темпе поступления последовательности дискретных отсчетов S(kΔ) без увеличения частоты дискретизации в десятки и сотни раз, как того требуют способы востановления с использованием аппроксимирующих полиномов нулевого порядка (ступенчатая аппроксимация) и первого порядка (кусочно-линейная аппроксимация).
Реализация преобразований во временной области на основании (8) должна базироваться на уверенности, что в процессе восстановления периодизированного сигнала S(t) по его отсчетам S(kΔ) спектр восстановленного сигнала совпадает со спектром сигнала, подвергнутого дискретизации.
Для этого на основании (8) определим спектр выходного сигнала восстанавливающего устройства

где  - ядро Дирихле [Справочник по математике. Корн Г., Корн Т. М.: Наука, 1973, стр.160].
- ядро Дирихле [Справочник по математике. Корн Г., Корн Т. М.: Наука, 1973, стр.160].
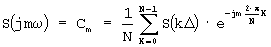 - ДПФ сигнала S(t);
- ДПФ сигнала S(t);
 - частотный коэффициент передачи восстанавливающего устройства.
- частотный коэффициент передачи восстанавливающего устройства.
Из уравнения (9) следует, что использование для востановления исходного сигнала в качестве базисных функций равноамплитудных полиномов в виде ядра Дирихле обеспечивает неискаженное воспроизведение частотных компонентов восстанавливаемого сигнала.
Однако высокая степень неискаженного восстановления исходного сигнала, потенциально заложенная в уравнение (9), может быть достигнута при условии, что задержанные выборки ядра Дирихле будут являться точными копиями, а так как

то очевидно, что для получения задержанных копий должны быть удовлетворены два условия:
1. амплитуды всех  суммируемых гармонических колебаний кратных частот nω должны быть равны и стабильны;
суммируемых гармонических колебаний кратных частот nω должны быть равны и стабильны;
2. управление формой задерживаемых копий должно производиться одновременным изменением углов фазовых сдвигов всех суммируемых колебаний кратных частот.
Возможность синтеза задержанных копий  непосредственным суммированием
непосредственным суммированием  гармонических колебаний кратных частот, генерируемых
гармонических колебаний кратных частот, генерируемых  генераторами, требует
генераторами, требует  систем автоматической стабилизации параметров колебаний (амплитуд, кратных частот и начальных фаз), а потому труднореализуема.
систем автоматической стабилизации параметров колебаний (амплитуд, кратных частот и начальных фаз), а потому труднореализуема.
Однако известное соотношение [Таблицы интегралов и другие математические формулы. Двайт Г.В. "Наука", М., 1966, стр.82]

применительно к анализируемой функции  позволяет изменить характер преобразований при ее формировании.
позволяет изменить характер преобразований при ее формировании.
Действительно представление функции  в виде
в виде 
позволяет трактовать ее как амплитудно-модулированное (AM) колебание, т.к. формально AM колебание представляет произведение огибающей Um(t) и гармонического заполнения. В (11) функцию гармонического заполнения (т.е. колебания несущей частоты) выполняет колебание  , где
, где  - частота повторения равноамплитудного полинома.
- частота повторения равноамплитудного полинома.
Функцию огибающей Um(t) выполняет периодическое колебание  представляющее отношение мгновенных значений синусоидальных колебаний с кратностью частот
представляющее отношение мгновенных значений синусоидальных колебаний с кратностью частот  , равной числу суммируемых колебаний. Такое представление функции
, равной числу суммируемых колебаний. Такое представление функции  позволяет для ее формирования использовать не
позволяет для ее формирования использовать не  генераторов колебаний кратных частот, а всего лишь один с частотой колебаний
генераторов колебаний кратных частот, а всего лишь один с частотой колебаний 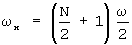 , стабильность параметров колебаний которого можно обеспечить известными методами.
, стабильность параметров колебаний которого можно обеспечить известными методами.
Для обеспечения закона изменения огибающей AM-колебаний 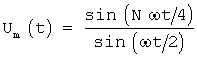 колебания несущей частоты
колебания несущей частоты  и неизменной амплитуды Um подают на вход масштабного преобразователя на операционном усилителе (ОУ), коэффициент передачи которого, определяемый отношением сопротивлений ku=Roc/R1 (где Roc - сопротивление резистора, включенного между выходом и инвертирующим входом ОУ, a R1 - сопротивление резистора, включенного между инвертирующим входом и выходом источника сигнала), изменяют переключением резисторов Roc в моменты прохождения колебаниями несущей частоты через нулевые мгновенные значения, что обеспечивает постоянство ku внутри интервала, равного половине периода колебаний несущей частоты.
и неизменной амплитуды Um подают на вход масштабного преобразователя на операционном усилителе (ОУ), коэффициент передачи которого, определяемый отношением сопротивлений ku=Roc/R1 (где Roc - сопротивление резистора, включенного между выходом и инвертирующим входом ОУ, a R1 - сопротивление резистора, включенного между инвертирующим входом и выходом источника сигнала), изменяют переключением резисторов Roc в моменты прохождения колебаниями несущей частоты через нулевые мгновенные значения, что обеспечивает постоянство ku внутри интервала, равного половине периода колебаний несущей частоты.
Из сопоставления левой и правой частей формулы (11) следует, что изменением начальной фазы ϕ0 колебаний несущей частоты  достигается одновременное изменение на ту же самую величину начальной фазы каждого из
достигается одновременное изменение на ту же самую величину начальной фазы каждого из  суммируемых колебаний кратных частот kω. Это означает, что изменением начальной фазы колебаний несущей частоты можно управлять временным положением AM колебания. Действительно, аргумент колебаний несущей частоты
суммируемых колебаний кратных частот kω. Это означает, что изменением начальной фазы колебаний несущей частоты можно управлять временным положением AM колебания. Действительно, аргумент колебаний несущей частоты  может быть представлен следующим образом:
может быть представлен следующим образом:
 ,
,
где  , откуда очевидно, что изменением угла фазового сдвига ϕ0 колебаний несущей частоты можно в широких пределах управлять задержкой во времени AM колебаний, воспроизводящих функцию
, откуда очевидно, что изменением угла фазового сдвига ϕ0 колебаний несущей частоты можно в широких пределах управлять задержкой во времени AM колебаний, воспроизводящих функцию  . В частности для обеспечения задержки функции
. В частности для обеспечения задержки функции  на величину, равную половине периода колебаний несущей частоты
на величину, равную половине периода колебаний несущей частоты  , необходимо изменить угол фазового сдвига колебаний несущей частоты ϕ0 на величину
, необходимо изменить угол фазового сдвига колебаний несущей частоты ϕ0 на величину 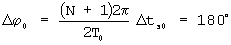 .
.
В этом случае для воспроизведения функции  , где К=0; 1; 2; ...; (N+2) достаточно резисторами Roc и R1 масштабного преобразователя канала с номером "l" обеспечить значение коэффициента передачи
, где К=0; 1; 2; ...; (N+2) достаточно резисторами Roc и R1 масштабного преобразователя канала с номером "l" обеспечить значение коэффициента передачи  , пропорциональное соответствующему значению огибающей AM колебания
, пропорциональное соответствующему значению огибающей AM колебания  , что обеспечивает получение отсчетов весовой функции в моменты прохождения колебаниями несущей частоты положительных и отрицательных максимальных значений.
, что обеспечивает получение отсчетов весовой функции в моменты прохождения колебаниями несущей частоты положительных и отрицательных максимальных значений.
Так как функция  представляет собой сумму из
представляет собой сумму из  гармонических колебаний кратных частот (т.е. высшей частотой в ее спектре является
гармонических колебаний кратных частот (т.е. высшей частотой в ее спектре является  ), то на основании теоремы Котельникова [Радиотехнические цепи и сигналы. Баскаков С.И. М.: Высшая школа, 1988, стр.117] отсчеты функции должны следовать через интервалы времени
), то на основании теоремы Котельникова [Радиотехнические цепи и сигналы. Баскаков С.И. М.: Высшая школа, 1988, стр.117] отсчеты функции должны следовать через интервалы времени 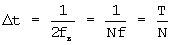 , а число отсчетов на периоде повторения функции
, а число отсчетов на периоде повторения функции  составляет
составляет 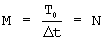 .
.
При использовании для получения отсчетов интервалов времени Δt, равных четвертой части периода несущих колебаний  , система отсчетов удовлетворяет теореме Котельникова, т.к.
, система отсчетов удовлетворяет теореме Котельникова, т.к.  . Но если при этом в качестве отсчетных точек выбрать точки перехода через ноль функции
. Но если при этом в качестве отсчетных точек выбрать точки перехода через ноль функции  и точки ее прохождения через положительные и N отрицательные максимумы, то половина отсчетов
и точки ее прохождения через положительные и N отрицательные максимумы, то половина отсчетов  соответствует точкам перехода
соответствует точкам перехода  через ноль и может быть обеспечена коммутацией выходного зажима с шиной нулевого потенциала. Остальные "
через ноль и может быть обеспечена коммутацией выходного зажима с шиной нулевого потенциала. Остальные " " отсчетов функции
" отсчетов функции  получаются в результате коммутации резисторов формирователей AM - колебаний.
получаются в результате коммутации резисторов формирователей AM - колебаний.
Таким образом использование амплитудно-модулированного колебания
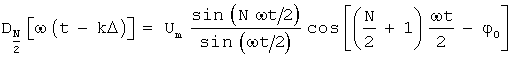
для реализации процедуры восстановления исходного сигнала (8) позволяет удовлетворить одновременно требованию малой нестабильности амплитуд и фаз всех " " гармоник его образующих.
" гармоник его образующих.
Действительно, т.к. AM колебание формируется из гармонических колебаний несущей частоты, нестабильность амплитуды которых  , то наибольшая погрешность задания AM колебания соответствует моментам времени, когда амплитуда модуляции достигает максимального значения
, то наибольшая погрешность задания AM колебания соответствует моментам времени, когда амплитуда модуляции достигает максимального значения  а потому изменения R1(0) и Roc(0) вследствие воздействия дестабилизирующих факторов вызывают относительные изменения коэффициента передачи
а потому изменения R1(0) и Roc(0) вследствие воздействия дестабилизирующих факторов вызывают относительные изменения коэффициента передачи
 .
.
Отсюда следует, что точность задания коэффициента передачи масштабного преобразователя определяется стабильностью резисторного делителя, т.е. достижимым технологическим уровнем долговременной стабильности резисторов, что позволяет на 1÷2 порядка повысить точность воспроизведения равноамплитудных полиномов по сравнению с вариантом генерирования "N" гармонических колебаний кратных частот и равных амплитуд и непосредственного их суммирования.
Возможность уменьшения погрешности задания угла фазового сдвига заложена в том, что требуемая величина дискрета временной задержки Δtз0=T/(N+2) AM колебаний обеспечивается путем изменения угла фазового сдвига  , что реализуется путем использования в качестве отсчетных значений функции
, что реализуется путем использования в качестве отсчетных значений функции  положительных или отрицательных максимальных ее значений, которые могут быть получены путем инвертирования (т.е. изменения фазы на противоположную) выходного напряжения масштабного преобразователя однокаскадным усилителем с коэффициентом усиления Кu=-1. Эта операция реализуется без погрешностей в широком диапазоне частот, что является гарантом точного воспроизведения задержанных реализаций функции
положительных или отрицательных максимальных ее значений, которые могут быть получены путем инвертирования (т.е. изменения фазы на противоположную) выходного напряжения масштабного преобразователя однокаскадным усилителем с коэффициентом усиления Кu=-1. Эта операция реализуется без погрешностей в широком диапазоне частот, что является гарантом точного воспроизведения задержанных реализаций функции  .
.
Изложенное в связи с поставленной задачей, а также в связи с предполагаемыми функциями конкретных измерительно-преобразовательных устройств структурной схемы позволяет сделать вывод о том, что замена процедуры определения коэффициентов дискретного преобразования Фурье, требующей одновременного участия всех дискретных отсчетов восстанавливаемого сигнала, на процедуру задания угла фазового сдвига колебаний несущей частоты равноамплитудного полинома

с дискретом Δϕ0=180° и последовательной обработкой каждого из дискретных отсчетов восстанавливаемого сигнала имеет основание для утверждения о повышении точности.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ФИЛЬТРАЦИИ ИЗМЕРИТЕЛЬНЫХ СИГНАЛОВ | 2003 |
|
RU2251791C2 |
| СПОСОБ ФИЛЬТРАЦИИ ИЗМЕРИТЕЛЬНЫХ СИГНАЛОВ | 2010 |
|
RU2462814C2 |
| СПОСОБ КАЛИБРОВКИ ИЗМЕРИТЕЛЯ КОЭФФИЦИЕНТА АМПЛИТУДНОЙ МОДУЛЯЦИИ | 2000 |
|
RU2190231C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ИЗМЕРИТЕЛЬНЫХ КАНАЛОВ ИНФОРМАЦИОННО-ИЗМЕРИТЕЛЬНЫХ СИСТЕМ | 2000 |
|
RU2200959C2 |
| УСТРОЙСТВО И СПОСОБ ПРЕОБРАЗОВАНИЯ ЗВУКОВОГО СИГНАЛА В ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ, УСТРОЙСТВО И СПОСОБ МОДИФИКАЦИИ ПАРАМЕТРИЧЕСКОГО ПРЕДСТАВЛЕНИЯ, УСТРОЙСТВО И СПОСОБ СИНТЕЗА ПАРАМЕТРИЧЕСКОГО ПРЕДСТАВЛЕНИЯ ЗВУКОВОГО СИГНАЛА | 2009 |
|
RU2487426C2 |
| Способ спектрального анализа многочастотных периодических сигналов с использованием компенсации комбинационных составляющих | 2019 |
|
RU2730043C1 |
| СПОСОБ КОМПЕНСАЦИИ УЗКОПОЛОСНЫХ ПОМЕХ | 2004 |
|
RU2269201C2 |
| ИЗМЕРИТЕЛЬ ПАРАМЕТРОВ ГАРМОНИЧЕСКОГО СИГНАЛА | 2008 |
|
RU2368909C1 |
| СПОСОБ ДЕМОДУЛЯЦИИ КРАТКОВРЕМЕННЫХ СИГНАЛОВ С МНОГОУРОВНЕВОЙ АБСОЛЮТНОЙ ФАЗОВОЙ МОДУЛЯЦИЕЙ В УСЛОВИЯХ ЗАМИРАНИЙ | 2018 |
|
RU2684605C1 |
| СПОСОБ ОЦЕНКИ ЧАСТОТЫ ОДИНОЧНОГО ГАРМОНИЧЕСКОГО КОЛЕБАНИЯ В ОГРАНИЧЕННОМ ДИАПАЗОНЕ | 2012 |
|
RU2480847C1 |
Изобретение относится к цифровой технике: к восстановлению аналогового сигнала по его дискретным отчетам. Технический результат заключается в расширении методов востановления аналогового сигнала по его дискретным отчетам. Для этого умножают сумму четного числа N произведений текущих отчетных значений сигнала на соответствующие значения суммы N/2 запаздывающих членов ряда комплексного ряда Фурье на 2/N, причем мгновенные значения названной суммы ряда Фурье воспроизводят амплитудной модуляцией косинусоидальных колебаний несущей частоты, превышающей в (N+2)/4 раз круговую частоту сигнала длительности Т, с законом изменения огибающей амплитудно-модулированного колебания, определяемым отношением мгновенных значений синусоидальных колебаний равных амплитуд, частота делимого синусоидального колебания в N/4 раз выше круговой частоты сигнала длительности Т, а частота синусоидального колебания делителя в два раза ниже круговой частоты сигнала. 1 ил.
Способ восстановления исходных сигналов, заключающийся в том, что мгновенные значения восстанавливаемого сигнала формируют путем умножения суммы четного числа N произведений текущих отчетных значений сигнала на соответствующие значения суммы N/2 запаздывающих членов комплексного ряда Фурье на 2/N, отличающийся тем, что мгновенные значения названной суммы ряда Фурье воспроизводят амплитудной модуляцией косинусоидальных колебаний несущей частоты, превышающей в (N+2)/4 раз круговую частоту сигнала длительности Т, с законом изменения огибающей амплитудно-модулированного колебания, определяемым отношением мгновенных значений синусоидальных колебаний равных амплитуд, частота делимого синусоидального колебания в N/4 раз выше круговой частоты сигнала длительности Т, а частота синусоидального колебания делителя в два раза ниже круговой частоты сигнала.
| СПОСОБ ФОРМИРОВАНИЯ СИГНАЛОВ ПРОИЗВОЛЬНОЙ ФОРМЫ | 1991 |
|
RU2051414C1 |
| SU 4347250 A1, 23.07.1989 | |||
| Ручка для органов управления радиоаппаратуры | 1956 |
|
SU112632A1 |
| US 4121295, 17.10.1978. | |||
Авторы
Даты
2005-08-27—Публикация
2003-05-05—Подача