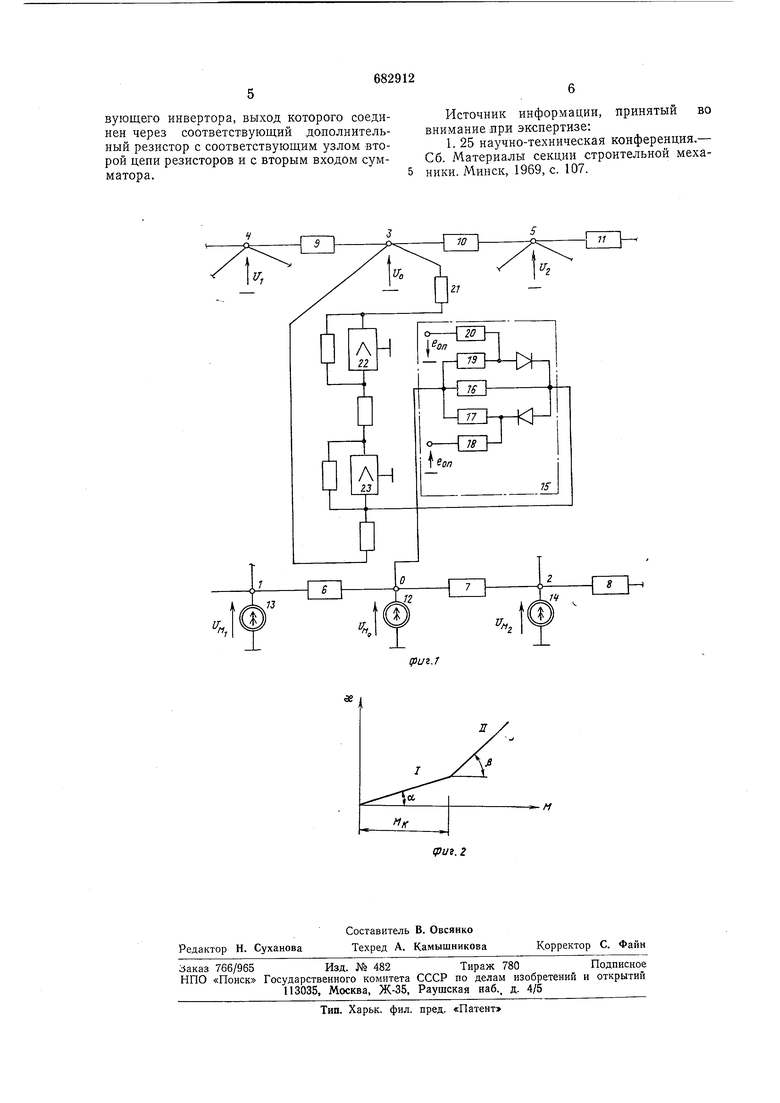
- 9. d;c где у - перемещение сечения балки; М - момент; X - кривизна; q - нагрузка на балку. Нелинейную зависимость .между кривизной и моментом аппроксимируем двумя участками прямых (фиг. 2). Тогда для Г участка а для П участка x +(M-yW,)f-,.V-j,-r- tg a, t гд« Eli - жесткость балки. Разбив балку на участки длиной /г, запишем уравнения (1) в конечно-разностной форме для двух участков диаграм.мы на фиг. 1 с учетом выражений (2,3). В связи с тем, что порядок г/, значительно меньше, чем Mi, приведем конечно-разностные уравнения к одному порядку, тогда - г/1 + 2г/о - г/2 - MO О, - М, + 2Мо - М - .- О, (4) - г/1 -f 2г/о - //2 - - Мо - (Жо-Мк) О, - М -Ь 2Afo - Afs - О, где Mi Mi Искомыми являются величины tji и Mi. Так как заранее .неизвестно, какая из систем уравнений (4) или (5) является действительной для данного узла балки, то нельзя заранее выяснить рабочую расчетную схему балки. Для моделирования иелинейной балки предназначено устройство, показанное на фиг. 1. Если материал балки работает в данном узле на участке I, то устройство определяется следующими зфавнениями . электрического тока: gU, + 2gU, + gU,-gU.,-g(o+UM,} -О, - . + 2gUM, - gUM, . (6) Если материал балки в данном узле работает на участке II, то устройство определяется следующими уравнениями электического тока: -gU, + 2gU, - gU., + gU, (b + U,,,}g-(,) - , во - , + - gUM, - 7о 0. Разделив уравнения (6, 7) на g, видим, что они аналогичны уравнениям (4, 5), 7- -€ если г/г , т EI, f 0,1,2, ,, , Ж , ё - где т - масштабный множитель; I/j - потенциал /-го узла верхней цепи резисторов; Им. - потенциал одноименного узла нижней цепи резисторов. При моделировании балки из физически нелинейного материала все одноименные узлы верхней и нижней, цепей резисторов соединяются между собой при помощи диодного функционального преобразователя, инвертора и сумматора напряжений, дополнительного резистора ло схедме на фиг. 1. Кроме того, реализуются граничные условия (шарнирное опирание, защемления и т. п.), что выполняется просто. Нагрузка на балку моделируется источниками тока 12-14. Устройство является мгновенно настраивающимся, обладает высокой степенью автоматизации решения рассматриваемой сложной конструктивно нелинейной задачи строительной механики. Формула изобретения Устройство для моделирования нелинейных балок, содержащее две цепи носледовательно соединенных резисторов, причем каждый общий ;вывод первой цепи резисторов соединен с источником тока и с входом соответствующего диодного функционального преобразователя, отличающееся тем, что, с целью повышения точности решения задачи, в него дополнительно введены резисторы, инверторы и сумматоры, причем выход каждого диодного функцио.нального преобразователя соединен с первым входом соответствующего сумматора, выход которого подключен к ВХОЛУ СОПТНРТГТвующего инвертора, выход которого соединен через соответствующий дополнительный резистор с соответствующим узлом второй цепи резисторов и с вторым входом сумматора.
Источник информации, принятый во внимание при экспертизе:
1. 25 научно-техническая конференция.- Сб. Материалы секции строительной мехаНИКИ. Минск, 1969, с. 107.

| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для моделирования сваи в грунте | 1977 |
|
SU622120A1 |
| Устройство для моделирования сжаторастянутого стержня | 1974 |
|
SU561974A1 |
| Устройство для моделирования узла рамы | 1975 |
|
SU561975A1 |
| Устройство для моделирования изгибаемого стержня | 1977 |
|
SU674050A1 |
| Устройство для моделирования балки на нелинейном упругом основании | 1977 |
|
SU682913A1 |
| Устройство для моделирования изгибаемого стержня на упругом основании | 1975 |
|
SU565307A1 |
| Устройство для моделирования стержня | 1977 |
|
SU746600A1 |
| Устройство для моделирования стержня | 1977 |
|
SU744651A1 |
| Функциональный преобразователь двух переменных | 1977 |
|
SU680000A1 |
| Устройство для моделирования пологих оболочек | 1976 |
|
SU601715A1 |


Авторы
Даты
1979-08-30—Публикация
1976-05-10—Подача