I
Изобретение относится к области вычислительной техники и может быть использовано при построении высокопроизводительных специализированных ИВМ, предназначенных для реализации преобразований линейной алгебры, в частности умножения матрицы на матрицу.
Известно арифметическое устройство специализированной вычислительной машины, работающей в системе счисления остаточных классов l , .и реализующей преобразование линейной алгебры, в частности умножения матрицы на матрицу. Недостатком такого АУ является сравнительно невысокое быстродействие и повышенный расход, оборудования, вызываемый тем,что, в частности, умножение матрицы на матрицу в нем связано с вычислением значений суммы .
Наиболее близким по технической сущности к изобретению является специализированная электронная счетная машина 2J, содержащая регистры исходных данных и
результатов, управляющие входы-выходы которых соединены с входом-выходом блока управления, блок памяти, сумматор-вы- читатель, умно ситель, причем выходы регистров исходных данных соединены с соответствующими входами умножителя и сумматора-вычитателя, выход которого соединен со входом первого регистра результата, выход блока памяти соединен с первыми входами регистров исходных данных -3.
Недостатком такой машины является ее низкая производительность. При решении большого числа прикладных задач в конечном счете приходится иметь дело с системами линейных уравнений с очень большим числом переменных (до 10 переменных). В результате возникает необходимость в выполнении операций над матрицами того же порядка, что и решаемые системы уравнений, т.е. порядка 10 .
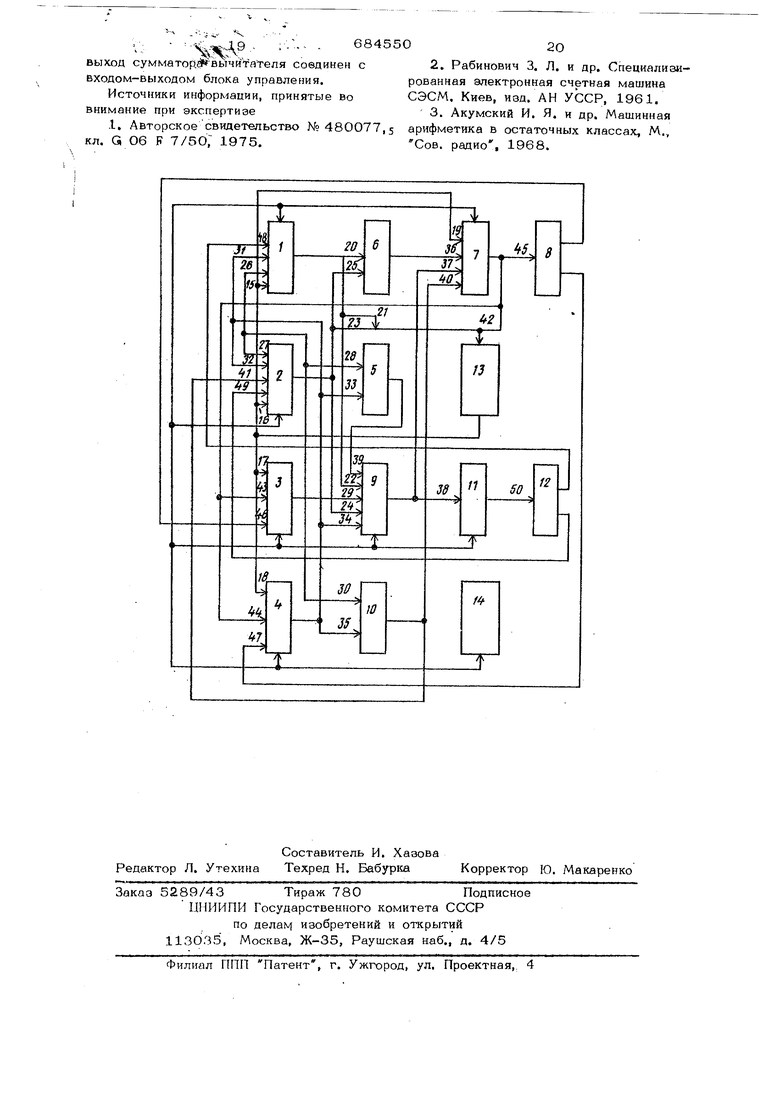
Вычисление значения суммы о Ь традиционными методами в этом случае требует значительных временных затрат. 368 Целью изобретения является повышение 11роиаволита17ьности устройства. Поставленная цель достигается введением в предложенный процессор дешифратора констант нулевизации, дешифратора свертывания матрицы, дешифратора промежуточных преобразований развертывания матрицы, дешифратора развертывания матрицы и второго регистра результата. При .этом выходы первого и второго регистров исходных данных через дешифратор свертывания матрицы соединены с первым входом второго регистра результата, второй вход которого соединен с вы ходом сумматора-.вычитателя. Выход умножителя соединен с третьим входом второго регистра результата и вторым входом второго регистра исходных данных. Четвертый вход второго регистра результата соединен с выходом блока памяти, а выход - с вхо- дом блока памяти, вторыми входами третьего и четвертого регистров исходных данных и через дешифратор промежуточных преобразований развертывания матрицы с третьими входами третьего и четвертого регистров исходных данных, выходы кото рых соединены с третьим и четвертым вхо дами первого и второго регистров исходны данных и через дешифратор констант ну певизации с пятым входом, сумматора-вы- читателя. Выход первого регистра результата соединен через дешифратор развертывания матрицы с пятыми входами первого и второго регистров .исходных данных, выходы Которых соединены с входом блока памяти. Управляющий вход-выход сумматора-вычитателя соединен с входом-выходом блока управления. Структурная схема специализированного процессора показана на чертеже . Процессор содержит регистры 1 -- 4 исходных данных, дешифратор 5 констант нулевизации, дешифратор 6 свертывания матрицы, второй регистр 7 результата, дешифратор 8 промежуточных преобразований развертывания матрицы, сумматор-вычитатель 9, умножитель 10, первь.й регистр 11 результата, дешифратор 12 развертывания матрицы, блок памяти 13, блок 14 управления, каналы 15 19, по которым информация из блока памяти 13 поступает в регистры 1 -4 и 7 соответственно, каналы 20 - 22, по которым информация из регистра 1 поступает в дешифратор 6, блок памяти 13 и сумматор-.вычитатель. 9 соответственно, каналы 23 25, по которым информация из регистра 2 поступает Э, блок памяти 13, с,мматор вычитатель 04 9и дешифратор 6 соответственно, каналы 26 - 30, по которым информация иа регистра 3 поступает в регистр 1 и 2, дешифратор 5, сумматор-вычитатель 9 и умножитель 1О соответственно, каналы 31 35, по которым информация поступает из регистра 4 в регистры 1 и 2, дешифратор 5, сумматор-вычитатель 9 и умножитель 10соответственно, канал 36, по которому информация с дешифратора 6 поступает на регистр 7, каналы 37, 38, по которым информация ия сумматора-вычитателя 9 поступает на регистры 7 и 11 соответственно, канал 39, по которому информация с выхода дешифратора 5 поступает на вход сумматора-вычитателя 9, каналы 40, 41, по которым информация с выхода умножителя 10 поступает на входы регистров 7 и 2 соответственно, каналы 44 - 43, по которым информация с выхода регистра 7 поступает на вход блока памяти 13,, вход дешифратора 8 и входы регистров 3 и 4 соответственно, каналы 46,47, по которым информация с .выхода дешифратора 8 поступает на входы регистров 3 и 4 соответственно, каналы 48, 49, по которым информация с выхода дешифратора 12 поступает на входы регистров 1 и 2 соответственно, канал 50, по которому информация с выхода регистра 11 поступает на вход дешифратора 12. Для данного специализированного процессора принципиально важное значение имеет выбор способа представления перерабатываемой информации. В качестве такого способа использована система счисления остаточных классов (ССОК). Главным преимуществом ССОК в данном процессоре являются удобство выполнения преобразования.исходной матрицы к отвечающему ей действительному числу, простота выполнения умножения и удобство перехода от действительного числа к отвечающей ему матрице. В соответствии с выбором ССОК каждьм из дешифраторов 5, 6, 8 и 12 представляет собой некоторый набор дешифраторов по каждому из модулей 1. ,Рц. выбранной ССОК. Сумматор-вычитатель 9 содержит k модульных сумматоров-вычитателей, выполняющих сложение (вычи-тание) по соответствующим модулям Р.,и Умножитель 10 содержит k множительных схем пп модулям Т,... Рь. Регист- оы 1-4, 7 и 11 рассчитаны на прием и хранение чисел представленных в ССОК, с диаазоном, состоящим из k модулей. Цифра о каящому пялпапу такой ССОК представ 5684 лена в двоичной системе счУ1сления. Длина ретистра н с.ютветствеяно схем суммато)а-вычитателя, умножителя и дешифра торов рассчитана на рабочий диапазон с К модулями, удовлетворяющий условию представления матрицы - результата умно жения в виде одного действительного числа. Этот диапазон обычно определяется 2.Г) гп двоичными разрядами, где ппорядок матрицы, am- количество дво- ичных разрядов представления элементов чисел матрицы. Процессор работает в трех основных режимах; -преобразование исходных матриц к , обеспечивающему эффективное выполнение собствергно операции умножения, -умножение матриц, -преобразование некоторого специального способа представления матрицы, явля ющейся результатом умножения матриц, к исходному виду. Кроме того, на основании предлагаемого устройства в случае необходимости может быть также выполнено преобразование исходной информации из позиционной систе мы счисления в ССОК и из ССОК в позиционную систему счисления, а также из ССОК одного типа в ССОК другого типа (операция расширения представления чисел в ССОК). Работа процессора в режиме преобразования исходных матриц к виду, обеспечивающему эффективное выполнение операции умножения, состоит в следующем. Предположим, что числовая информация представляющая элементы исходных матри записана в блок памяти в ССОК диапазона Р . Предположим также, что преобразовывается матрица М следующего вида: Преобразование исходной матрицы к виду, обеспечивающему эффективное выполнение операции умножения матриц, связано с использованием двух стандартных операцийоперации свертывания строк и операции свертывания столбцов. Суишость операции свертываниястрок покажем на примере свертывания двух Ьерхних строк матрицы fA . В качестве исходной для преобразования информации используем квадратную матрицу М второго Порядка, являющуюся некоторым элементом двух рассмотренных строк матрицы fA : При выполнении операции свертывания матрицы М строк элементы записываются соответственно в регистры 3 и 4 процессора. Действительные числа, представляющие элементы а и я, , как и все числа, представляющие остальные элеме 1ты матрицы М заданы в диапазоне Р В результате операции свертывания р выполняемой над матрицей М элементы Я и О;) 2. заменяются одним элементом - действительным числом диапазона Q Р . ,Для этого также должны элементы о( быть предварительно представлены в этом диапазоне Ц . Таков представление в процессоре выполняется на основе регистров 1-7, сумматора-вычитателя 9 и дещифратора 5. При этом используется известный алгоритм (так называемый алго- pj нулевизации), описанный, например выражении (З). Для реализации этого алгорить5а- требуется - ( сложение, где - количество модулей ССОК диапазона Р . Расщиренное представление элементов записывается соответственно в регистры 1 и 2. На их место в регистры 3,4 записывается следующая пара элементов Qji 32 матрицы М . После получения расширенного представления элементов а, и а, начинае-гся Выполнение собственно операции свертывания строк. При выполнении этой операции информация из регистров 1,2 подается на дешифратор 6.Дешифратор б реализует таблицу соответствия такого типа, при котором паре входных q ,, , а 2 ставится в соответствие действигельное число, отвечающее комплексному числу вида flepexon от комплексного нясла к действнTt;;ibnoKty может быть выполнен, например, в соответствии с правилами, описанными в выражении (З). Информация с выхода дешифратора 6 поступает на регистр 7. Из регистра 7 она переписывается в блок па мяти. Действительное число, с помощью которого заменяется комплексное число, требует для своего представления в два раза больше количества двоичных элементов блока памяти, чем этого требуют действительная и мнимая части комплексного числа. Из этого следует, что замена комп лексного числа действительным никаких изменений объема блока памяти не требуе Те ячейки, которые использовались для хранения комплексного числа, теперь используются для хранения действительного числа. Числа Рт . С(2 с регистров 3,2 соответственно подаются на сумматорвычитатель 9 {сложение выполняется в диапазоне Р }, и полученная на его выходе сумма ( а21 записывается в регистр 7 с последующей перезаписью в регистр 3, Числа CI22 О1я регистров 4 и 1 соответственно подаются на сумматорвычитательЭ Счисло а вычитаетсяизчисла ч 5 . Полученная на его выходе разность записывается в регистр 7 с последующей перезаписью в регистр 4. Проведенные преобразования соответствуют представлению исходной квадратной матрицы в следующем виде:
0()1
«.. ,
0(022 - а jj.
5 .
Как уже отмечалось, матрица
.1 -«1г «п °-.и заменяется действительным числом. На этом кончается первый цикл стандартной операции свертывания двух верхних строк матрицы М . Дальнейшее преобразование матрицы М связано с использованием матрицы
.ао) 31
(4)
(2Г°11 ьг.
о -.г -
где А , Д - члены, учитываюпгае результаты предыдущих преобразований. От этой матрицы в соответствии с описанными вьппе преобразованиями осуществляетея
переход к матрице
f(
(«па-) °
) -(о, Кг-Л) () та матрица получена так. 1 качсстг о л( ого CTo;ifUa ваяг ненулевой столбиц второго слагаемого в выражении (З). В качестве правого столбца исполь сювапы элеенты a-ji , двух верхних ютрок атрицыМ, Применим преобразования к матрице (4), аналогичные тем, которые имели месо в первом цикле стандартной операции свертывания строк проводимой над матрицей (2). Третий цикл преобразований связан с использованием матрицы вида (,) правый столбец которой получен дописыванием к левому столбцу, полученному при выполнении второго цикла, очередных элементов а. , двух верхних строк матрицы ,W . После реализации некоторого числа циклов преобразований промежуточной матрицы в конечном счете получим матрицу вида о а„, tj Этой матрице ставится в соответствие действительное число, отвечающее матрицеи, таким образом, в полученное представ ление матрицы М вносится некоторая погрешность. Заметим (это важно при выполнении обратного представления форм представления результата умножения к матрице исходного порядка), что замена матрицы () О ( А) о на матрицу ()-(c.,) («пИА) эквивалентна дописыванию в первой и вто рой строках исходной матрицы К элемен тов -Ор2 f щ А соотве ственно. Числовые значения этих элементов с их знаками, находящиеся в регист рах 1,2, переписываются в блок памяти. Процедура, примененная к первой и второй строкам матрицы М , повторяетс затем кЗи4,5и6и т.д. строкам. Причем если порядок матрицы М нечет ньй, добавляется строка, все элементы которой принимают нулевое .значение. в результате применения описанной процедуры ко всем строкам матрицы М Получается некоторая новая матрица с вдвое меньшим числом строк, .ролученная матрица представляет исходную матрицу М с погрешностью, определяемой введе нием дополнительного столбца в матрицу М , из соответствующих дополнительны элементов , получаемых в результате ука занных преобразований строк. Если описанную процедуру преобразования строк применить теперь (соответствующим образом) к столбцам, их число также буде уменьшено вдвое. Особенность использевания описанной процедуры состоит в том, что теперь уже берутся не две вер них строки матрицы М . а два ее крайних столбца - первый и второй. И элементы, над которыми выполняется циклическая onepauHHi выбираются от верхних к нижним. Полученная таким образом матрица представляет исходную с погрешностью, эквивалентной введению в исходную матр цу М некоторой дополнительной строки с элементами, получаемыми в результате преобразования столбцов. Эта дополнительная строка в матрице записывается как ее нижняя строка. Итак, в результате выполнения описанных преобрааованнй матрицы N1 справа налево и сверху вниз , исходная матрица порядка п сводится к матрице порядка -2Последовательное применение этого преобразования позволяет свести с некоторой погрешностью исходную матрицу произвольно1Х) порядка, к матрице первого по5йдка, т.е. заменить с некоторой погрешностью исходную матрицу некоторым действительным числом, В результате выполнение операций над матрииакш может быть сведено к операциям над действительными числами. В частности, умножение двух матриц может быть заменено умножением двух действительных чисел. Возникающая здесь погрешность результата из-за погрешности сведения исходных матриц к действительным Числам может быть ликвидирована при обратном преобразовании дей- ствительного числа - результата умножения к матрице исходного вида. В случае, когда выполняется умножение двух матриц (например, матрицы А на матрицу 5 )- матрица-мноншмое А преобразуется, начиная со строк, а матрицамножитель В - начиная со столбцов. Дополнительная строка матрицы А и дополнительньй столбец матрицы Ь в образовании элементов искомой матрицы-произведения не используется, и, таким образом, эти строка и столбец в -образовании, погреишости не участвуют. При выполнении описанных преобразований матриц элементы дополнительной строки матрицымножимого, и элементы дополнительного столбца матрицы-множителя в блоке памяти не запоминаются и в процессе вычисления не используются. Умножение матриц, представленных действительными числами .выполняется известными методами перемножения двух действительных чисел. В предлагаемом процессоре оно выполняется в ССОК - одно из чисел записывается в регистр 3, а второе - в регистр 4, Результат умножения с выхода умножителя 10 запис1:)В;1ется в блок памяти.
11
Рассмотрим работу предлагаемого процессора в режиме обратного преобразования специального представления матрицы к исходному виду, т.е. в режиме, когда от действительного числа, представляюшего некоторую матрицу, осуществляется переход к этой матрице. Указанный перехоц от числа к матрице связан и в случае свертывания матрицы к числу, с использованием двух стандартных операцийопепации развертывания столбцов и операции развертывания строк.
Действительное число (обозначим его через О. ) из блока памяти записывается в регистр 7. Определяем комплексное число /. - f J которое соответствует
этому действительному числу о . Переход от действительного числа к-, Комплексному числу может быть выполнен, например, с правилами, описанными в выражении (З).
Из регистра 7 число 4 поступает на дешифратор 8, в KofbpOM структурно зафиксирована таблица перехода от действигелыюго числа к числам Г иг , удовлетворяющим условию э (тос( ) fs (c(mod р2 -f ) где о. ч Ь - соответственно действительная и мнимая части рассматриваемого комплексного числа (в данном случае комп лексное число Q имеет только действительную часть, которая совпадает с а(, мнимая часть равна нулю, т.е. bi О ). Величина ( Р 4 q )норма комплексного числа-диапазона, по которому определяется наименьший вычет комплексного числа О . С выхода дешифратора 8 числа Г , подаются на регистры 3 и 4, где их представление с помощью сумматора-вычитателя 9, регист ров 1 и 2 и дешифратора 5 расширяется от диапазона представления в ССОК с комплексными модулями с нормой ( р2 + cj, ).до диапазона с нормой N, ( р - ) , где N , удовлетворяет условию 1. - ()
в 84
12
Число г и I , предст,чвлениь Р в ССОК, Комплексный диапазон которой ик:еет норму N, записываются в регистр 11, откуда они подаются на дешифра1ор 12. Этот дещифратор построен так, что каждой паре Гиг на ег-о выходе появляются действительная О, и мнимая of« части наименьшего вычета кo плeкcнoгo. числа по комплексному модулю, норма которого равна М . Итак, с выхода дешифратора 12 Р, и а 2. соответственно записываются в регистры 1 и 2, Выполненное преобразование действительного числа а можно условно рассматривать
как развертывание действительного числа, представляющего .результрт умножения исходных матриц, в матрицу вида
а)
П
Полезной информацией для нахождения искомой матрицы является часть матрицы (7), а именно верхняя ее строка. Нижняя строка является избыточной, в результате чего она может быть опущена. Итак, описанное выше преобразование позволило Поставить в соответствие действительное число а матрице (8). h а, , Дальнейшее развертывание матрицы (8) связано с выполнением стандартной операции развертьшания строк матрицы, Сушность этой операции состоит в следующем. Возьмем число 02 из регистра 2. При этом учитывается то, что число О, -f Это условие накладывает отпечаток на описанную процедуру тем,что ССОК, в которой проводятся преобразования, имеет диапазон, в два раза меньший, чем диапазон при развертывании числа р (здесь сравнение диапазонов осуществляется в логарифмическом масштабе). Вы полним над этим числом аналогичную описанной выше процедуру замену его комплексным числом. Затем о-- комплексного числа .соответствующего О перейдем к матрице вида 10-aj Поскольку а является элементом крайнеГо правого столбца развертываемой матрицы (8), то нравьй столбец матрицы (9) отбрасывается и для дальнейших нреобрааований рассматривается матрица Далее ,число а также заменяется комплексным числом, которое соответствует матрице /. /-1 1 Суммируем матрицу 110 с матрицей (.11 ...так, что матрица-результат будет иметь ./ (о1-а;).ь; (а .а)) 6 Указанное суммирование выполняется с помощью регистров 1-4 и 7 и сумматоравычитателя 9. На этом-.оканчивается од им i цикл стандартной операции развертывания строк матрицы. Полученная матрица (12) соответствует действительному числу С) . Если это действительное число Q рассматривать как частный случай матрицы, то число q есть матрица первого порядка. Описанная процедура позволила перейти от матриц первого порядка к соответствующей ей /1о п матрице второго порядка (12). Для учета погрешности, возникающей в представлении результата умножения из-за погрешности сведения исходных матриц к действитель-: ным числам, элементы полученной матрицы скорректируем следующим образом. Из каж дого элемента этой матрицы вычтем произ ведение соответствующих элементов столбцов множимого и, строк множителя, которые были записаны в блок памяти для уче та погрешности, возникающей при выполнении операции прямого преобразования исходных матриц-сомножителей в действительный числа. Для учета поправки к элементу-О, пищам из блока памяти в регистры 3, 4 соответст-венно числа а | и Ь , представляющие столбец и строку исходных матриц, записанных для коррекции. G8 за O Содержимое регистров 3,4 подается на умножитель 10. Результат умножения за- писывается в регистр 2 , Содержимое регистров и и 1 подается на сумматор вы- читатель (содержимое регистра 2 вычитается из содержимого регистра 1). Результат операции записывается в регистр 7 с Последующей перезаписью в оперативную память. Для учета поправки к а перепишем этот элемент из блока памяти в регистр 1. В регистр 3 запишем Ьлл столбца множимого, записанного в. оперативную память на этапе прямого преобразования исходной матрицы в число для коррекции, Содержих.ое регистров 3,4 (соответственно числа-02 . ) подаются на ум{1ожитель 10. Результат умножения запись вается в регистр 2, Содержимое регистров 2 вычитается ;:э содержимого ,регистра 1 на сумматоре-вычитателе. Ре- . - зультат операции записывается в регистр 7 с последующей перезаписью в блок памятл. Аналогично корректируются элементы Ь и Ь матрицы, причем при вычисляется поправкорректировкеCS.o, ifexp jQ P корректировке b - попоавка Ь-э-} 1i Э3. 1аким образом, результатом описанных преобразованир является откорректированная матрица второго порядка видакорректированные значения элементов мат Дальнейщиепреобраоования связаны с переходом от матрицы (13) второго порядка к матрице четвертого порядка. Если описанную циклическую операцию преобразования строк (их развертывание/применить теперь соответствующим образом к столбцам матрицы (13), то их число будет увеличено вдвое. Особенность использования описанной операции состоит в том, что теперь берутся для чзвертывания не эл -ne MOiiT.i строк, a эломопты стольцов. Элементы над которыми выполняется эта цик лическая операцияJ выбираются от нижних элементов столбца к верхним. Применение операций развертывания ко всем столбпак матрицы (13) преобразует ее к матрице с удвоенным числом столбцов. Применим теперь к полученной матрице циклическую операцию развертывания строк. Эта операция увеличит число строк в матрице в два раза. Таким образом поочередное применение к матрице (13). циклических операций развертывания столбцов и строк позволило нам перейти от матрицы второго порядка (13) к мат рице четвертого порядка. Для полученной матрицы, как и для матрицы второго порядка, производим ликвидацию погрешности которая имеет место при переходе от работы с матрицами четвертого порядка к работе с матрицами второго порядка. С этой целью производим с элементами полученной матрицы четвертого порядка ана логичные операции ликвидации погрешности, которые имели место при ликвидации погрешности с элементами матриць второго порядка (13). Применяя к полученной матрице четвер того Порядка указанные циклические one- .рации развертывания столбцов и строк, а также операции ликвидации погрешности перейдем от матрицы четвертого порядка к матрице восьмого порядка. Аналогично переходим от матрицы восьмого порядка К матрице 16 порядка и т.д. до порядка, совпадающего с порядком исходных матриц. Использование предлагаемого матрич- Но-векторного процессора позволяет существенно увеличить эффективность переработки информации при реализации операций над матрицами и векторами. Так . в частности, анализ конкретных, задач, существенным образом испольауюшнх предлс женный процессор, показал следующее. При умножении матриц м -го порядка в предложенном матрично-векторном процессоре требуется ( умножений. 4 п сложений и г(,.) „4; операций «юшярения П)опстлилеиия чисел (онерапий иуловизации), где Дл - операция нулепиеу:1ции чисел элементов кв-щратной магрицы порядка h. ; число слагаемых в скобках выражения (14) равно ,Д - операция нулевизации чиселэлементов прямоугольной матрицы с длиной строкиг и длиной столбца П, Если m - число модулей ССОК, в которой представляются элементк квадратной матрицы порядка- п , то указанные операции нулевизацни для своей реализации требуютследующего числа сложений: для нулевизации Д требуется (т-1) сложений, Д- - (2т-1) слодля нулевизации для нулевизации гп ) сложений, а для нулевизации Д. -( -1) сложений. Подставив приведенные вьгше выражения в (14) увидим, что количество М операций сложения, имеющее место при кулевизациях, независимо от рассматриваемого порядка матрицы и диапазона представления чисел равно (п(т-Я)5(2т-1) р-я...+Й ()i(4-eogr2n)n2( сложений, а при гл -2 (типичный случай ju а (4Еоо 2 П )п , Итого для умножения матриц в нредлааемом процессоре требуется умножений ((-j} ,.. + (й:1| 6 П сложений (4йз§2п)п2+4п2 й()п2 Всего для реализации операций умножеия дпух матриц в предлагаемом процессое требуется -(,, П)п2-ц,бп2 модульных операций, в то время как клас сический метод перемножения матриц требует п умножений и п сложений действительных чисел. Аппаратурные затраты в предлагаемом процессоре определяются аппаратурными затратами на п процессоров с диапазс ном до 30 двоичных разрядов. Общий объем ЗУ этих процессоров, кэмеряется объемом, необходимым для хранения перемножаемых матриц в их обычно исходном представлении. Однако можно ввести избыточность в процессор, которая позволи1;ь не учитывать погрешность и тогда происходит дополнительное повышение производительности, В этом случае требуется выполнение одной операции умножения и ( ) П сложений деиствительных чисел в ССОК, Увеличение объема блока памяти процессора позволяет отказаться от выполне- нения операций расширения (нулевизации) представления 1 и Г . при развертывании чисел в матрице и комплексных составляющих а и «2. при сворачивании матрицы в действительное число. Тогда для умножения матриц потоебуется одна операция умножения и 4 П. сложений действительных чисел в ССОК. Следует отметить, что в предложенном процессоре с целью экономии аппаратуры можно не сворачивать матрицу по однбго действительного числа, а лишь сократить ее ПОРЯДОК, тогда в процессоре при перемножении матриц добавится еще вы11олнение (А , . , операций умножения н (у) операций сложения, где k - число, показывающее во сколько раз уменьшается порядок матриц. Производительность в этом случае растет по кубическому закону, а аппаратурные затраты - по квадратному закону по сравнению с изменением коэффициента сокращения порядка матрицы. Так если процессор сокращает порядок матрицы в 2 раза, то при этом производительность повышается в 8 раз, а аппаратурные затраты - в 4 раза. Если порядок матрицы сокращается в 8 раз, соответст венно производительность повышается в 512 раз и затраты на аппаратуру - в 64 рааа и т.д. Необходимо отметить, что предложенное сокращение количества операций умно жения и сложения приводит к увеличению разрядности обрабатываемых чисел. Возникает трудность, состоящая в реализа-. ции этих операций в огромном диапазоне. Однако использование в вычислениях ССОК позволяет ликвидировать этот недостаток, сведя, например, время выполнения операции умножения {в этом случае) ко времени умножения двух остатков по модулю, двоичное представление которого измеряется обычно 8-16 разрядами. Формула изобретения Специализированный процессор, содержащий регистры исходных данных и результатов, управляющие входы-выходы ко- торых соединены с входом-выходом блока управления, блок. гшмяти умматор-вычитатель и умножитель, причем выходы регистров исходных данных соединены с соответствующими входами умножителя и.. сумматора-вычитателя, выход которого соединен со входом первого регистра результата, выход блока памяти, соединен с первыми входами регистров исходных данных, отличающийся тем, что, с целью повышения производительности, в него введены дешифратор констант нулевизации, дешифратор свертывания матрицы, дешифратор промежуточных преобразований ра8вертывания матрицы, дешифратор развертывания матрицы и вто- рой регистр результата, причем выходы первого и второго регистров исходных данных через дешифратор свертывания матрицы соединены с первым входом второго регистра результата, второй вход которого соединен с выходом сумматоравычнтателя, выход .умножителя соединен с третьим Входом второго регистра результата и вторым Входом второго регистра исходных данных, четвертый вход второго регистра результата соединен с выходом блока памяти, а выход - с входом блока памяти, Вторыми входами третьего и четвертого регистров исходных данных и через дешифратор промежуточных преобразований развертывания матрицы - с третьими входами третьего и четвертого ре гистров исходных данных, выходы которых соединены с третьим и четвертым входами первого и второго регистров исходных данных и через дешифратор констант н певизации с пятым входом сумматора-41Ычитате ш, выход первого регистра результата соединен через дешифратор развёртывания матрицы с пятыми вхоДами первого и второго регистров исходнь1х данных, выходы которых соединены с входом блока памяти, управляющий входвыход сумматор вычитателя соединен с входом-выходом блока управления. Источники информации, принятые во внимание при экспертизе 1. Авторское свидетельство №480077,5
кл. G Об F 7/50, 1975.
Сов. радио, 1968. 2.Рабинович 3. Л. и др. Специализированная электронная счетная машина СЭСМ. Киев, изд. АН УССР, 1961. 3.Акумский И. Я. и др. Машинная арифметика в остаточных классах, М.,








| название | год | авторы | номер документа |
|---|---|---|---|
| Цифровая адаптивная антенная система | 1990 |
|
SU1810943A1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ МОДУЛЯ M-МЕРНОГО ВЕКТОРА | 1995 |
|
RU2080650C1 |
| СИСТОЛИЧЕСКИЙ ПРОЦЕССОР ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ С КОРРЕКЦИЕЙ ОШИБКИ | 1992 |
|
RU2018950C1 |
| Устройство для умножения | 1986 |
|
SU1432506A1 |
| Устройство для вычисления двумерного быстрого преобразования Фурье | 1986 |
|
SU1408442A1 |
| Запоминающее устройство с переменным форматом данных | 1981 |
|
SU987678A1 |
| АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ХАРТЛИ-ФУРЬЕ | 1999 |
|
RU2190874C2 |
| Арифметическое устройство для процессоров быстрого преобразования Фурье | 1983 |
|
SU1116434A1 |
| Устройство для оценки степени оптимальности размещения в многопроцессорных кубических циклических системах при направленной передаче информации | 2017 |
|
RU2727555C2 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ МОДУЛЯ M-МЕРНОГО ВЕКТОРА | 1992 |
|
RU2029356C1 |


Авторы
Даты
1979-09-05—Публикация
1977-01-03—Подача