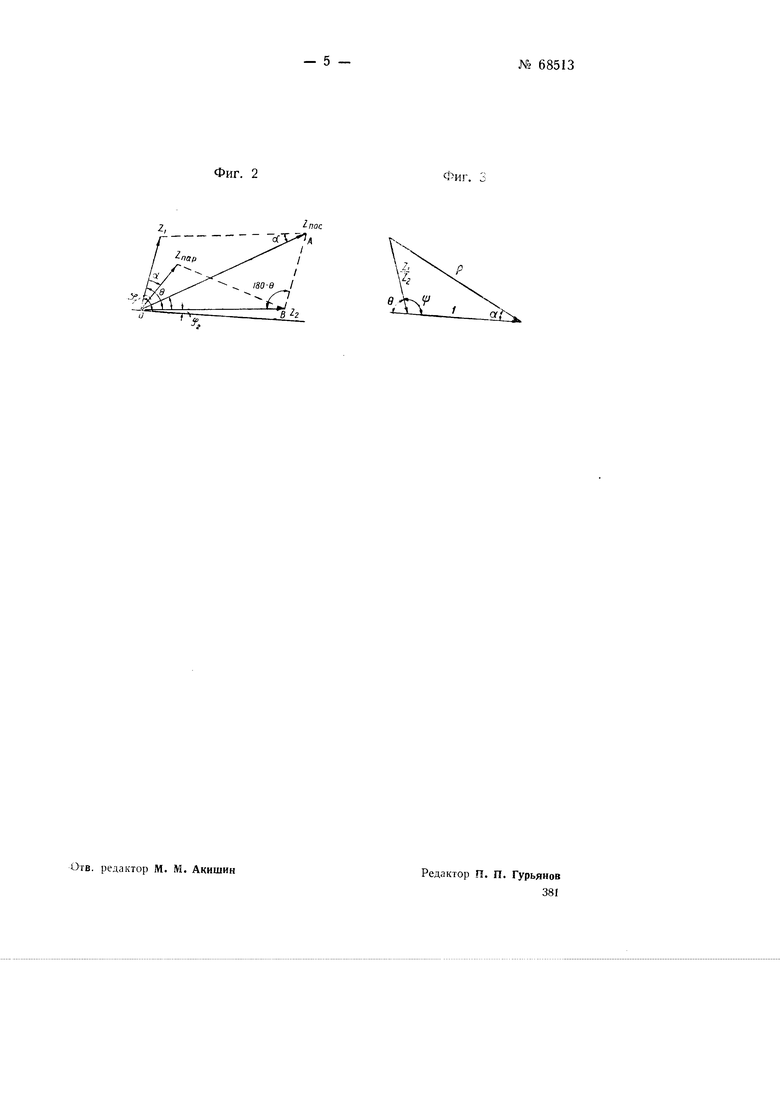
Предлагаемый прибор для расчета электрических цепей (определения величин и фаз сопротивлений эквивалентных двум последовательно или параллельно включенным импеданцам), показанный на фиг. 1, состоит из основания А, на котором нанесены две дуговые шкалы, разделенные одна на градусы от О до 180° и другая от О до 90°. и двух линеек S и С, поворотных на шарнире D, центр которого совпадает с точкой пересечения линий тп и fb. Обе линейки имеют вырезы, которые служат для правильной установки линейки С. В нижнем (узком) вырезе линейки С помещается выступ, установленный на основании А прибора. С помощью этого выступа и нижнего выреза линей и С достигается передвижение обеих линеек и поворот их под любым углом. На линейках нанесены деления, служащие для их установки и отсчета искомых величин. Расстояние от центра шарнира D до точки а на линейке С соответствует одной условной единице и разделено на 100 равных частей. Расстояние от того же центра шарнира до точки & на другой линейке В равно удвоенному отрезку Da и разделено на 200 равных частей. При изготовлении прибора материалом для основания и линеек могут служить целлулоид, прессшпан, латунь и ряд других материалов с нормальным коэфициентом линейного расширения. В основу конструкции предлагаемого прибора положены следующие предпосылки, поясняемые фиг. 2 и 3. Предположим, требуется определить полное сопротивление, эквивалентное последовательно и параллельно включенным полным сопротивлениям:- 75 -, Jf., и -, где Za Zi (фиг. 2). Введем обозначения: fi - (pz . Zfioc Zi-Z, Zi + Zj
Отношение
ZfJOC Zi -(- 2 Zl I 1 f/14
I .Ill
z,z, z.
Так как частное от деления двух комплексов равно комплексу, то последнее равенство можно переписать в виде:
ZnrcУ ,, . . ч
-j- e-e e(cosa + /sma) йли учитывая, что
1 ZiE Zi j(vi-vi) Zi je
7 J 7 7
Za Z,f
(cosб+ /sine),
можно представить равенство (1) в виде:
p(cosa + /sin а)
|-(cos0 + /sin0j+ I. Из полученного равенства следует:
g -cosa - COS0+ 1
Zi
Q sma -„- sin I
Zo
Воспользуемся последним равенством. Из треугольника ОАВ следует:
sin а sin(6/-а)
/1
sinfl
-7I/41)
%2cose.|i.
Подставляя найденное значение sin а в (2) получаем:
+ (g-)42|i.cos9
или, вводя угол
180-е.
5 |/l + (.cosv. (3)
1 -7
2,/
Z.,
Подкоренное выражение представляет собой не что иное, как квадрат
стороны треугольника со сторонами -
И /, образующими угол у (фиг. 3).
378
Изложенное выше представляет собой доказательство теоремы, которую можно сформулировать следующим образом:
Если построить треугольник по
Zi
двум сторонам, равным 7 и -,
2
И углу ip, образованному этими сторонами и равному 180 - i + 92 то третья сторона Q треугольника и угол, образованный сторонами е и 7, будут представлять собой модуль и аргумент комплексного сопротивления, которое, будучи умножено на комплекс Zg, даст полное сопротивление, эквивалентное последовательному соединению комплексов:
Zj, Z,. и Za Za , где Z, Zi,
а при умножении его обратной величины на комплекс Z даст полное сопротивление, эквивалентное параллельному соединению комплексов Z
и Zg.
Использование предлагаемого прибора при расчетах различных электрических цепей позволяет свести тру(2) доемкий и утомительный процесс вычисления электрических величин к простым механическим и арифметическим действиям.
Расчеты электрических цепей с помощью этого прибора не только занимают во много раз меньшее время и не утомляют лиц, производящих расчеты, но и дают более точные значения определяемых величин и в значительно меньшей степени, чем обычные аналитические расчеты, подвергаются влиянию тех факторов, которые могут приводить к крупным ошибкам.
Процесс определения Znoc и Znap по формулам
Zl
Z.Zo-e. HZn«p
JO
Q -e
заключается в следующем:
1.Определяют отношение - (Zj
2
ДОЛЖНО быть меньше Zj) и разность
fi-Vz2.Устанавливают линейку С так,
Z, чтобы прямая тп была наклонена к
2 горизонтальной линии шкалы основаНИЯ под углом, равным (pz, и
деление, соответствующее отношению
у
-, совпало с центром шарнира D.
2
3. Сохраняя неизменным положение линейки С, поворачивают линейку В так, чтобы прямая /& пересекала горизонтальную линию шкалы основания в крайней правой точке, и читают по шкале линейки В значение е и по шкале градусов (от О до 90°) значени угла а. 4. Умножая о на Zz, получают Znoc и, беря отношение Z к Q, определяют Znap.
Для пояснения описанного способа может быть приведен пример определения Znoc и Znap цепи, составленной из последовательно и параллельно соединенных сопротивлений
600Й и Z2 1500e Так как Z 600 , то 1 600 -04
Z., 1500 И е 2 - y-i 55°-0°- 55°.
Устанавливая деление 0,4 шкалы линейки С против точки на выступе основания и направляя прямую тп 1 К, чтобы она совпала с отметками на большой шкале основания, соответствуюш;ими 55°, получаем:
е 1,273 и а 15°. Таким образом,
, Z е - 1909,5 и
7Zi /171 -3 J15
Znap .„ 471,3
Q.E
Опыт показывает, что решение этой задачи обычным способом и с помощью арифмометра и таблиц тригонометрических функций занимает 35 минут, вместо двух минут, затрачиваемых на решение при помощи предлагаемого прибора, и дает следующие точные решения:
7„„, 1908, г„„р 471,.
Таким образом, относительная погрешность вычисления при помощи этого прибора не превышает 0,04%.
Лица, не имеющие еще достаточной практики работы с прибором, могут испытывать некоторое затруднение при определении знаков фазовых углов Znoc и Znap
При этом определении следует руководствоваться следующим:
а)фазовый угол при последовательном соединении равен , а при параллельном соединении , причем угол а может быть как положительным, jaK и ртрицательным;
б)векторы Znoc и Znap находятся между векторами Z и Z, причем вектор Znoc примыкает к большему вектору Zj, а вектор Znap к меньшему вектору Zj.
Можно пользоваться и таким способом безошибочного определения знака угла а:
,sine
tga ,
COS 9+1 l
а так как всегда больше единицы,
то знак а определяется только знаком sin 9. При этом необходимо иметь в виду, что при определении фазового угла Znap
в Pz а при определении фазового угла Znoc
e pz - piЭто относится к векторным диаграммам, подобным диаграмме, изображенной на фиг. 2. Однако, любую другую векторную диаграмму можно свести к диаграмме, показанной на фиг. 2, путем вращения начальной оси и компенсации этого вращения прибавлением к фазовым углам Znoc и Znap или вычитанием из них угла, на который повернута начальная ось.
Если sin Q оказывается величиной положительной, то фазовый угол равен разности между и а, если же sin 0 величина отрицательная, то фазовый угол равен сумме 951 ч-з и а.
Прибор позволяет решать и обратную задачу, т. е. разлагать импедан379цы на их составляющие или опреде лять одну из составляющих по общему полнежу сопротивлению и выбранной второй составляющей. Предмет изобретения Прибор для расчета электрических цепей (определения величин и фаз сопротивлений, эквивалентных двум последовательно или параллельно включенным импеданцам) отличающийся тем что он состоит из основания Л, на котором нанесены две дуговые шкалы разделенные одна на градусы от О до 180° и другая от О до 90°, и двух поворотных на шарнире D линеек В и С, связанных одна с другой при помощи выступа,, установленного на основании и проходящего через продольные пазы в обеих линейках из коих одна (С) на участке от центра шарнира D до конца линейки, соответствующем одной условной единице, разделена на 100 равных
Фиг. 1
90 частей, а другая (В) на участке от центра того же шарнира/) до конца линейки, равном удвоенному участку на линейке С, разделена на 200 равных с тем, чтобы определение ZnocM Znap ПО формулам; .р-е Z, И г„ар ё осуществлялось путем установки линейки С под углом к горизонтальной линии на шкале основания А,. соответствующим разности - 9а так. чтобы деление на линейке С, соответствующее отношению совпадало с центром шарнира D, и поворотом при неизменном положении линейки С, линейки В так, чтобы она пересекала горизонтальную линию на шкале основания в крайней равой точке с тем, чтобы деление на инейке В соответствовало значению р деление на градусной шкале (от О о 90°) основания А - значению а.
Фиг. 2
Фиг. 3



| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для расчетов величины и местоположения балансировочного груза на телах вращения | 1946 |
|
SU70814A1 |
| СЧЕТНОЕ УСТРОЙСТВО | 1946 |
|
SU70052A1 |
| Устройство для измерения импеданцев | 1944 |
|
SU78894A1 |
| Способ измерения внутренних сопротивлений источников электрического тока | 1944 |
|
SU83576A1 |
| Устройство для измерения сопротивления заземления | 1944 |
|
SU67395A1 |
| Прибор для построения аксонометрических проекций объекта | 1972 |
|
SU449830A1 |
| Синусно-косинусный потенциометр | 1952 |
|
SU105948A1 |
| Прибор для измерения остойчивости | 1990 |
|
SU1815654A1 |
| Прибор для расчета электрических цепей СВЧ | 1982 |
|
SU1049924A1 |
| Расчетный прибор для определения тока возбуждения синхронных машин под нагрузкой | 1936 |
|
SU50614A1 |


2,
.Ь.
Авторы
Даты
1947-01-01—Публикация
1945-05-22—Подача