Счетные устройства, состоящие из квадратного основания с нанесенной равномерной сетчатой шкалой, поворотно закрепленных в вершинах квадрата, двух прозрачных линеек с визирной чертой и градусных шкал для установки линеек, уже известны. Эти устройства предназначены для вычислительных действий, основанных на известной зависимости между элементами подобных прямоугольных треугольников, отсекаемых на квадрате линейками.
Предлагаемое счетное устройство от известных отличается тем, что одна из линеек выполнена в виде крестовины с продольным прорезом для ее перемещения относительно беи в вершине квадрата и нанесенной второй перпендикулярной визирной чертой с равномерной шкалой.
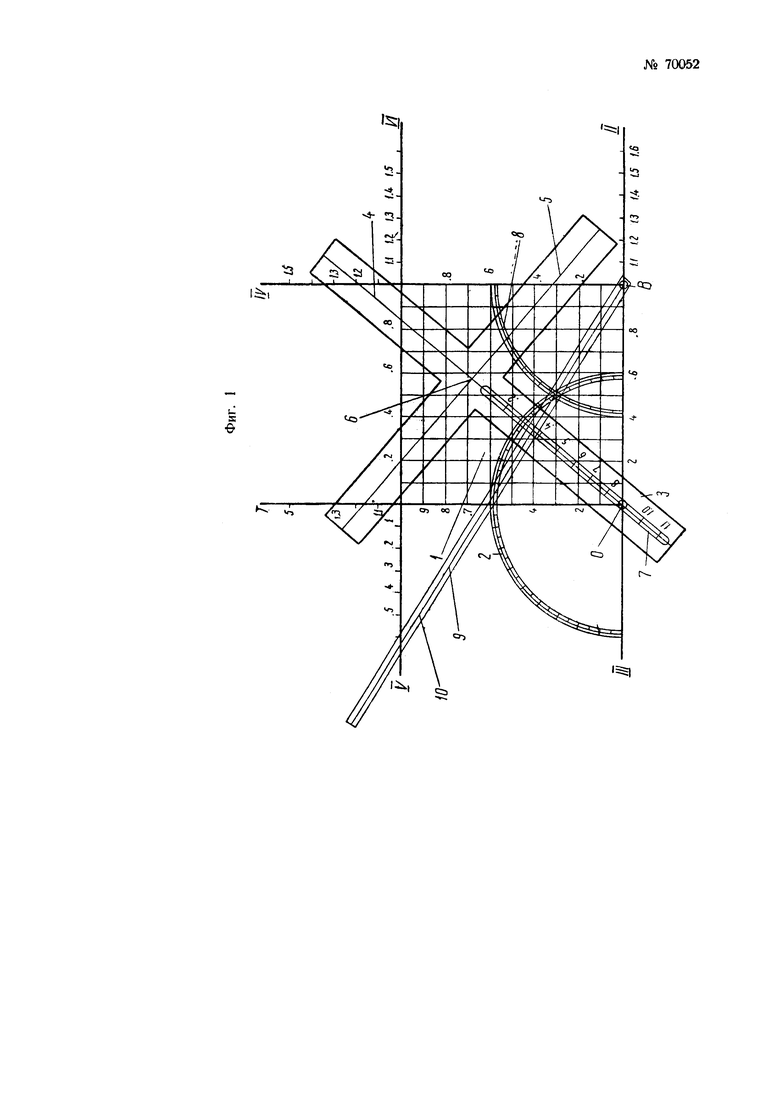
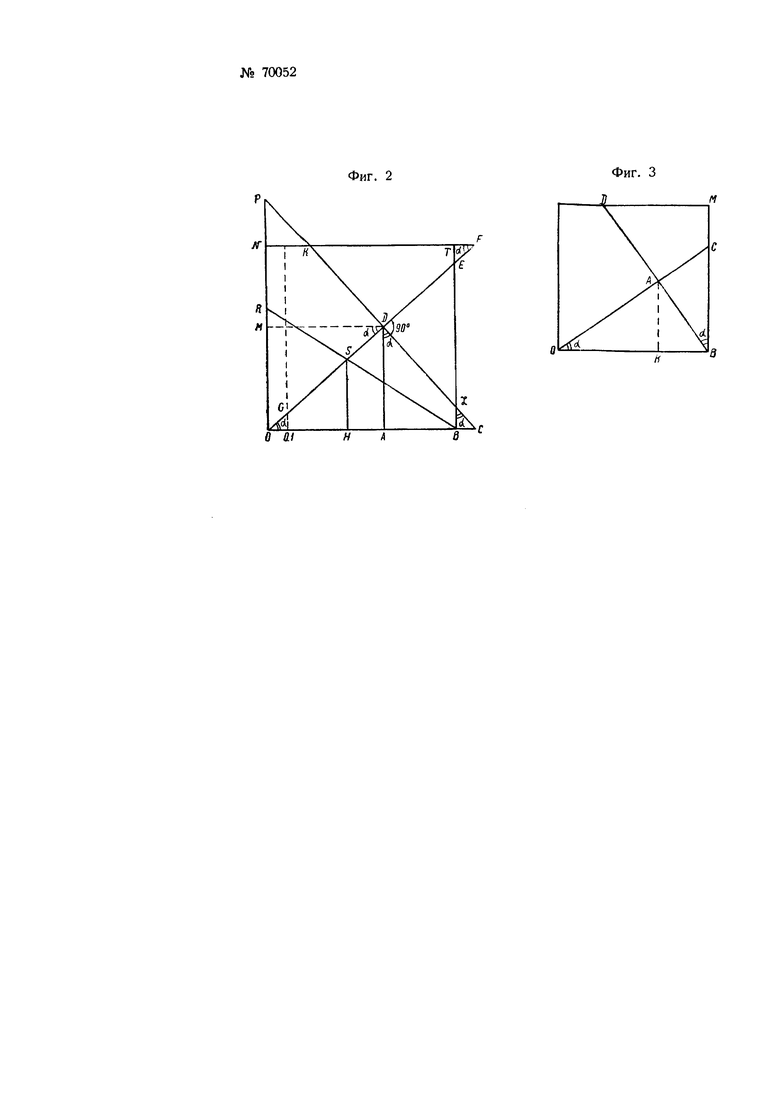
На фиг. 1 изображена схема предлагаемого счетного устройства; на фиг. 2 и 3 - схемы отсекания на квадрате устройства подобных прямоугольных треугольников, предназначенных для ведения расчетов.
Устройство состоит из квадратного основания 1 с нанесенной равномерной сеткой, образованной взаимно перпендикулярными прямыми, проведенными через десятые и сотые деления сторон квадрата. На продолжениях сторон квадрата нанесены равномерные шкалы I, II, III, IV, V и VI.
В вершине О квадрата, снабженной градусной шкалой 2, закреплена крестовина 3 с продольным прорезом 7 для ее перемещения относительно оси, расположенной в вершине О. На крестовине нанесены взаимно перпендикулярные визирные черты 4 и 5, пересекающиеся в точке 6, служащей началом равномерных шкал, нанесенных вдоль этих черт. В вершине В, снабженной градусной шкалой 8, поворотно закреплена линейка 9, снабженная визирной чертой 10, с нанесенной вдоль черты шкалой. Линейка 9 и крестовина 3 выполнены из прозрачного материала.
При помощи предлагаемого счетного устройства можно выполнять следующие математические расчеты.
Умножение (фиг. 2):
ВЕ·ОА=AD,
BE·OD=CD,
OG·OD=OI·ОС.
Деление:
BE=CD:OD,
BE=AO:OA,
DP=OD:BE.
Извлечение квадратного корня из суммы или разности квадратов двух чисел:
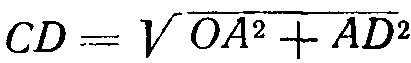
Определение тригонометрических величин (фиг. 3):
sin α=АВ,
cos α=OA,
tg α=ВС.
Извлечение квадратного корня из произведения двух чисел (фиг. 2):
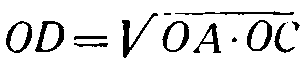
Произведение синуса на косинус (фиг. 3):
AK=ОА·АВ.
Извлечение квадратного корня (фиг. 2):
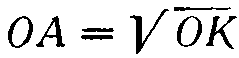
Возведение во вторую степень:
OK=ОА2,
ОС=OD2, если OA=0,1.
Возведение в третью степень:
CD=BE3 при условии, что
BE=DP.
Решение квадратных уравнений вида х2+рх-1=0:
OA2+АС·OA-1=0.
Из области электротехнических расчетов преобразование последовательного соединения активного и реактивного сопротивления в параллельное и наоборот:
 ;
;
 .
.
Определение сопротивления, эквивалентного двум параллельно включенным активным сопротивлениям или емкости, эквивалентной двум последовательно включенным конденсаторам:
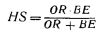
Ниже приводится пример определения емкости, эквивалентной емкости двух последовательно включенных конденсаторов; С1=3,75 мф и С2=2,56 мф.
Для этого линейка 9 и крестовина 3 устанавливаются так, чтобы черта 4 крестовины пересекла линию В-IV в точке 0,375, а черта 10 линейки 9 пересекла точку 0,256 на линии OI. Пересечение черт 4 и 10 дает точку, расстояние которой от линии III-II будет равно искомой емкости С, эквивалентной 1,52 мф.
| название | год | авторы | номер документа |
|---|---|---|---|
| Вычислительное устройство | 1980 |
|
SU911544A1 |
| Чертежный прибор | 1990 |
|
SU1750978A1 |
| Прибор для получения и нанесения координат при землемерных и топографических работах и для трансформирования фотоснимков | 1929 |
|
SU20329A1 |
| Прибор для решения штурманских задач | 1982 |
|
SU1068948A1 |
| Счетный логарифмический прибор | 1927 |
|
SU10545A1 |
| Логарифмическая счетная линейка | 1956 |
|
SU117763A1 |
| Счетный прибор | 1924 |
|
SU1655A1 |
| Счетный прибор | 1947 |
|
SU82753A1 |
| СЧЕТНЫЙ ЛОГАРИФМИЧЕСКИЙ ДИСК | 1923 |
|
SU3238A1 |
| УСТРОЙСТВО ДЛЯ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ | 1990 |
|
RU2028667C1 |
Счетное устройство, состоящее из квадратного основания с нанесенной равномерной сетчатой шкалой, поворотно-закрепленных в вершинах квадрата двух прозрачных линеек с визирной чертой и градусных шкал для установки линеек, отличающееся тем, что одна из линеек выполнена в виде крестовины с продольным прорезом для ее перемещения относительно оси в вершине квадрата и нанесенной второй перпендикулярной визирной чертой с равномерной шкалой.
Авторы
Даты
1948-01-31—Публикация
1946-06-08—Подача