(54) ЭЛЕКТРОННАЯ КЛАВИШНАЯ ВЫЧИСЛИТЕЛЬНАЯ МЙМИНА




| название | год | авторы | номер документа |
|---|---|---|---|
| Цифровой анализатор энергетического спектра | 1978 |
|
SU769443A1 |
| ЦИФРОВОЕ УСТРОЙСТВО ДЛЯ АДАПТИВНОЙ КОРРЕКЦИИ КВАДРАТУРНЫХ ДЕМОДУЛЯТОРОВ | 2000 |
|
RU2187140C2 |
| Электронная клавишная вычислительная машина | 1977 |
|
SU679986A1 |
| Электронная клавишная вычислительная машина | 1982 |
|
SU1068945A1 |
| Устройство для настройки систем автоматического регулирования | 1978 |
|
SU951242A1 |
| Устройство разрешения многозначности фазовых измерений | 1981 |
|
SU993146A1 |
| Многокомпонентные аэродинамические весы с вычислительным устройством | 1961 |
|
SU150301A1 |
| Устройство для обработки измеритель-НОй иНфОРМАции | 1978 |
|
SU807311A1 |
| ПРОЦЕССОР ДЛЯ ЦИФРОВОЙ СИСТЕМЫ ОБРАБОТКИ ДАННЫХ | 1971 |
|
SU305477A1 |
| Формирователь квазиоптимальных дискретно-частотных сигналов | 1988 |
|
SU1578836A1 |

1
Изобретение относится к областивычислительной техники и может быть использовано при йнженерно-техничес них и других расчетах.
Известны ЭКВМ, содержащие арифме тическое устройство с сумматором, операционными регистрами, регистром запятой, устройством знаков, устройством памяти, устройством управления операциями, устройством управления индикацией, блок индикации, блок клавиатуры и блок питания Ц.
Недостатком известной ЭКВМ является ограниченные функциональные возможности.
Наиболее близким по технической сущности к изобретению является ЭКВМ, содержащая блок клавиатуры, блок арифметических устройств, блок памяти, блок знаков, устройство управления индикацией, блок индикации, блок накопления операндов и результатов вычислений, блок управления, блок синхронизации и блок питания с соответствующими взаимосвязями.
Недостатком прототипа являются ограниченные возможности вычислений, исключающие расчет линейных дифференциальных уравнений и синтез передаточных функций линейных динамических систем.
Целью изобретения является расширение класса решаемых задач, что
5 позволит производить расчеты линейных дифференциальных уравнений с постоянными коэффициентами любого порядка и синтезировать передаточные функции линейных динамических систем.
Эта цель достигается тем, что в ЭКВМ, содержсодую блок клавиатуры, блок записи чисел, блок хране.ния знаков, буферный накопитель, блок
5 управления, память, арифметический блок, причем первый и второй выходы блока клавиатуЕ4л соединены соответственно с первьп ш входами блока записи чисел и блока управления, выход которого соединен с управляющими входами блока записи чисел, буферного накопителя, памяти, блока хранения знака и арифметического блока, выход блока записи чисел соединен с
25 первым информационным входом буферного накопителя, первый выход арифметического блока соединен с информационным входом памяти, введены блок вычисления масштаба, блок возведения
30 в степень, блок умножения на маси1табные коэффициенты, блок вычисления .коэффициентов, дешифратор дискретности, дешифратор значений функции и светодиодная матрица. Выход блока записи чи-сел соединен с первыми входами блока вычисления масштаба и блока умножения на масштабные коэффициенты выход которого через блок вычисления; коэффициентов соединен со вторым информационным входом буферного накопителя, выход которого соединен с первым входом арифметического блока, второй вход которого соединен с выходом блока хранения знаков. Второй выход арифметического блока, сигнальные выходы блока вычисления масштаба блока возведения в степень, блока умножения на масштабные коэффициенты и буферного накопителя соединены с соответствующим входом блока управления , выход которого соединен с управлягацими входами дешифратора дискретности и дешифратора значений функции, информационные входы которых соединены с соответствующими выходами памяти, а выходы - соответственно со входами столбцов и строк светодиодной матрицы. Информационный выход блока вычисления масштаба соединен со входом блока возведения в степень, выход которого соединен с информационным входом бло.ка умножения на масштабные коэффициенты.
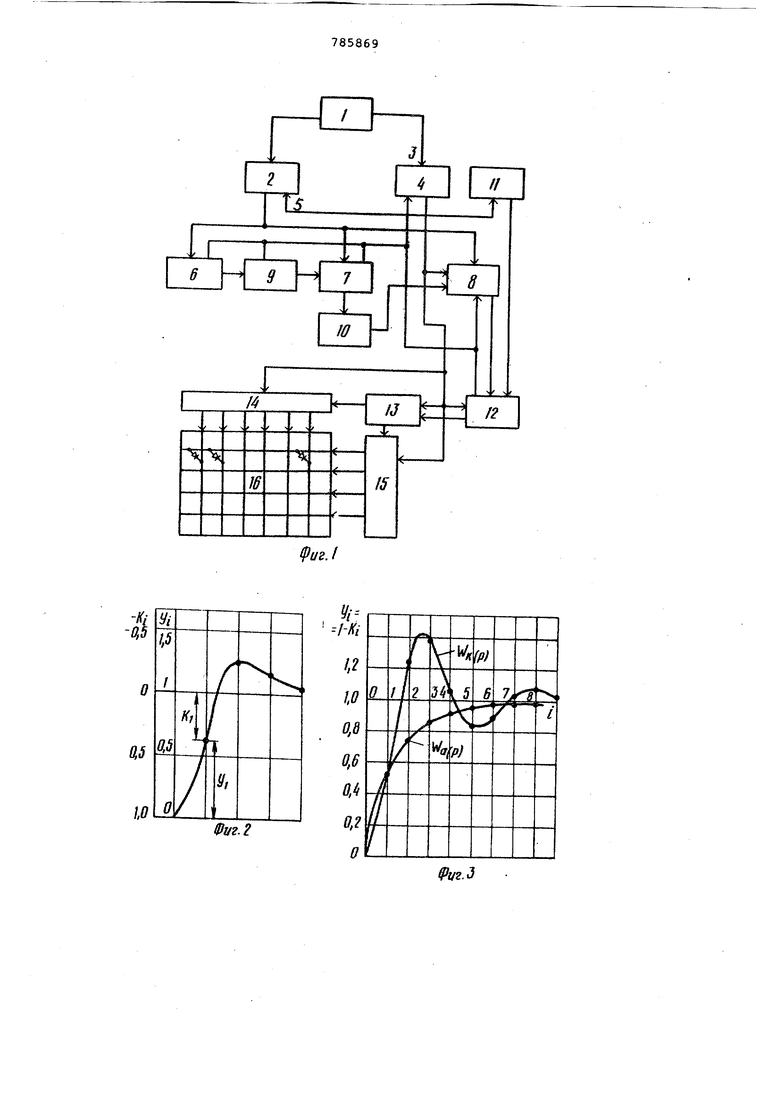
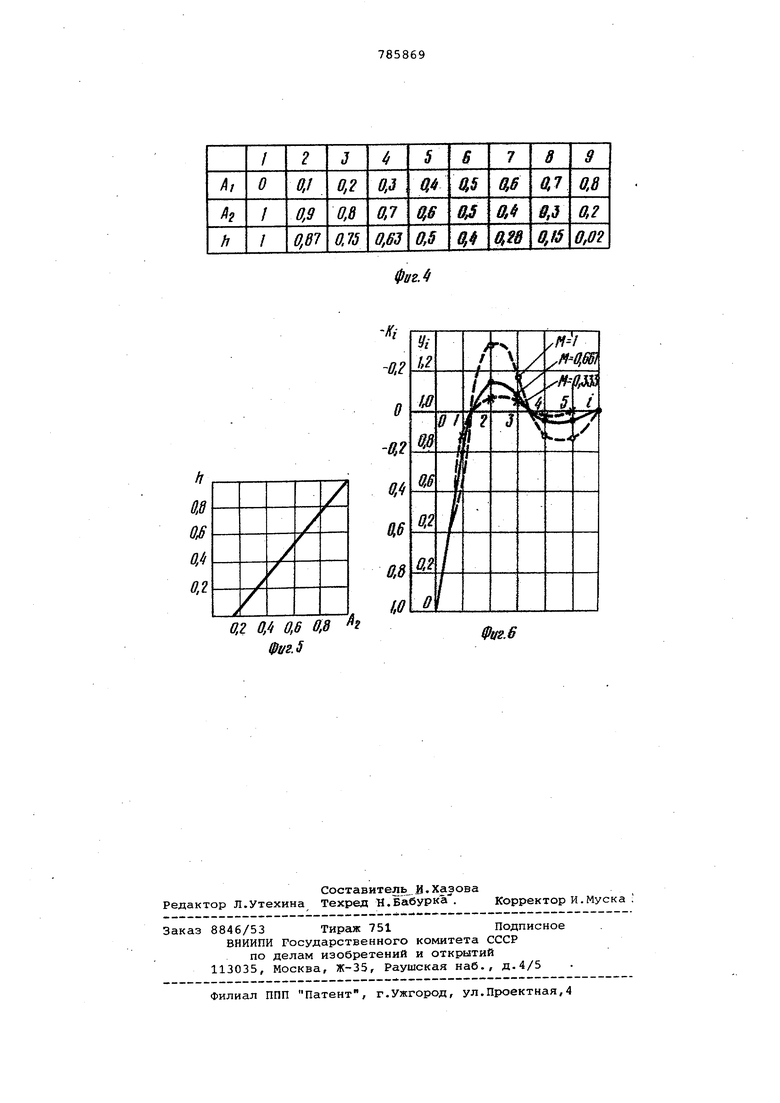
Функциональная схема ЭКВМ приведена на Лиг.; график переходной функции и ее дискретные значения, рассчитанные при правильно выбранном масштабе- - на фиг.2; графики и расчетные дискретные значения переходной -апериодической и колебательной функции - на фиг.З; таблица связи и перерегулирования переходной функции и коэффициентов передаточной функции - на фиг. 4, зависимость между коэффициентом передаточной Функции второго порядка и перерегулированием переходной функции - на фиг. 5 график переходной функции и расчетные ее значения при различных масштабах - на Лиг.6.
Блок 1 клавиатуры соединен со входом блока 2 записи чисел и входом 3 блока управления 4. Второй вход 5 блока 2 записи чисел подключен к . выходу блока управления 4, а выходы ко входу блока вычисления масштаба 6, входу блока 7 умножения на масштабные коэффициенты и входу буферного накопителя 8. Вход блока 6 вычисления масштаба подключен к выходу блока управления 4, а выход - к входу блока 9 возведения в степень, второй вход которого соединен с выходом блока управления 4, а выход - с входом блока управления и входом блока 7. Блок 7 подключен к входам блока управления 4 и входу блока 10 вычисления коэффициентов , второй вход которого подключен к выходу блока .
управления 4, а выходы соединены с входом блока хранения знаков 11 и входом буферного накопителя 8, подключенного к выходу блока управления 4 и входу арифметического блока 12, соединенного с выходом блока хранеНИН знаков 11, входом памяти 1 и входом блока управления 4. Блок хранения знаков 11 соединен с выходом блока управления 4. Память 13 соедииена с выходом блока управления 4
и входами дешифратора дискретности 14 и дешифратора значений функции 15, вторые входы которых подключены к выходу блока управления 4, а выходы к входам светодиодной матрицы 16.
Для вычисления переходной функции инейной динамической системы,описаной линейными дифференциальными уравениями(передаточной функцией)любого
.
порядка вида (p)-. .p:;
i aip4a,2pS--n3inp
установлена закономерная связь между коэффициентами передаточной функции и значениями переходной . функции в отдельных ее точках с дискретностью , выражающаяся следующим образом:
,
де Vi - дискретные значения переходной функции
К - коэффициенты, рассчитываемые по формулам
V iKj -K- a -ctj+b.
-- a r VS- r- i-A- i-2V- -i
Л-- масштаб времени, рассчитанный для апериодической переходной функции по формуле MQ: О,/ с и для колебательной переходной функции
по формуле
. -
М t 2qi Viaa) Вычисления в предложенном устройстве осуществляются следуюгцим образом.
С блока питания при включении выключателя питания подаются все необходимые питающие напряжения на блоки ЭКВМ и при нажатии на блоке клавиатуры кнопки Сброс через блок управления 4 выдается команда, приводящая блоки ЭКВМ в исходное состояние. Блок управления служит для выработки последовательности команд, необходимой для выполнения каждой операции и представляет собой регистры, состояние которых меняется по. специальной программе, .обеспечивающей выполнение операций. Порядок изменений состояния регистров определяется внутренними и внешними свя зями и зависит от алгоритма операци Блок управления вырабатывает сигнал управления работой блоков ЭКВМ. В блоке клавиатуры 1 на цифровых клавишах производится последователь ный набор коэффициентов линейнь1х ди ференциаильных уравнения О и Ъ и вспомогательных чисел 0,5,1 и 2, которые при нажатии операционных клавиша -, - , 0,5,1 и 2 записываютс в регистрах блока записи чисел. Вычисление апериодической перехо ной функции осуществляется следующи образом. Нажатием на блоке клавиату ры 1 операционных клавиш Масштаб MQ и Вычисление -по команде из блока управления 4 производится запись из блока 2 записи чисел в блок вычисления масштаба значения коэффициента а и операнда 0,5, в блок 7 всех значений коэффициентов, а в блок В значение операнда 1. , В блоке вычисления масштаба по формуле Mq - вычисляется масштаб времени. Конец операции вычисле ния масштаба сообщается в блок 4 управления, с которого выдается команда в блок 9 возведения в степень где масштаб последовательно возво-. дится в степень /А , ( и эти значения записываются в регистрах блока. Окончание вычислений из блока 9 возведения в степень передается в блок 4 управления, с которого вьадается команда начала счета в блок 7. В блоке 7 вычисляются коэффициенты AI и В, по Лормулам л,--Ала- и , которые записываются в регистрах блока 10 вычисления коэффициентов. Конец операции масштабирования коэАфициентов вьодается в.блок 4 управления, с которого поступает команда начала вычисления в блок 10 вычисления коэффициентов и последовательно вычисляются коэффициенты по формулам i-SN- 2 a. /V .. ,N-K..,...(.. Значения вычисленных коэффициентов записываются в блок 8, а знаки каждого коэффициента - в регистры блока 11. Окончание вычисления коэффициентов выдается в блok 4 управления который формирует команду выдачи операндов и результатов вычислений и знаков из блока 8 и блока 11 в арифметический блок 12, где производится вычисление по Формуле -1-к. Полученные значения (1)ункции Vj записываются в регистры памяти 13. Окончание вычисления передается в блок 4 управления, который Формирует команды передачи значений функции в дешифратор дискретности и дешифратор значений функций, в которых происходит преобразование значений функций и их номера дискретности в управляющие напряжения, подаваемь е на соответствующие входы светодиодной матрицы 16. Диоды матрицы высвечивают граЛ)ик переходной функции. Вычисление колебательной переходной функции в ЭКВМ осуществляется следующим образом. В блоке клавиатуры 1 на цифровых клавишах производится последовательный набор коэффициентов передаточной функции q,-, и вспомогательных чисел 0,5,1 и 2, коToptJG при нажатии операционных клавиш 01 , Ъ 0,5,1 и 2 записываются в регистрах блока 2 записи чисел. При нажатии операционных клавши Вычисление и Масштаб МК происходит запись коэффициентов Л, 1ft в блок 7, а коэффициентов 4,05. и операндов 1 и 2 в блок б вычисления масштаба, где производится вычисление масштаба по формуле Ч ( ± 2 2аа/ 0(4 Остальные операции по вычислению значений функции и индикации ее на светодиодной матрице совпадают с вычислениями апериодической переходной функции. Для оценки характеристик переходной функции достаточно рассчитать двадцать дискретных значений , следовательно, необходимо взять i 20, При этом дешифратор дискретности должен иметь двадцать выходов, а матрица - двадцать столбцов светодиодов. Точность определения переходной функции должна быть не хуже 5% (установившийся режим 0,05), следовательно, при максимальном перерегупировании, равном 1, необходимо име-i i ), а сорок значений функции светодиодная матрица должна иметь 40 строк светодиодов. Решение линейных дифференциальных уравнений для определения переходной ункции линейной динамической систеы указанным способом приводится первые, поэтому приведем его докаательство. Для передаточной функции вида «,,.1 - -I «a,, . оэффициенты К,- получаются путем оследовательных преобразований ,tp)f-Li-w(p), v(p),-vj,(p)j. ,4t) -- -f-tt-iM- -iP. примененных для установившегося ре жима N--°r. K,--K,a,,, 4 4°r4«a V. - . i-N-,.(,. Докажем, что существует масштаб вр мени М , при применении которого к коэффициентам передаточной функции Oi и Ъ коэффициенты дадут диск тные значения переходной Лункции 4J 1 (,фиг.2) . К передаточной функции /J (р) п мениг искусственный масштаб времен и получим передаточную функцию 1-1-Ьд В,р - ---+В „р ,р-,,рЧ... где/А --AAa,,-,j ,-; А„ ,, .Ъ ; в,.,-- w. Ьз,---) ,, коэффициенты которой равны к,.-в,, ,,,, ,,--к,-v;,A,г., Ц .Л-%-г2 - Известно,что форма кривой пере ной функции не зависит от искусст венного масштаба времени, т.е.фор кривой переходной функции, соотве твующая передаточной функции N3y(p) будет такой же, что и форма криво переходной функции, соответствующ переходной функции У р .Однако величины коэффициентов завися от масштаба времени. Запишем коэффициенты виде -Я,-В„ : ,.-(, ., 1 а Сравнивая эти коэффициенты с коэффициентами передаточной функц апериодического звена Мд (р) - .-,K.2.-X.2.Ai и т.д. с ко фициентами колебательного звена TT JTAIF , Кг Ai - Ki Аг , .--Кг-К.. видим, что коэффициенты , рас считанные для передаточной функци WH (р) f состоят из коэффициенто передаточной функцииЧ(/о( (р) и ) (р) других коэффициентов-добавок. Отс следует вывод, что форму кривой п реходной функции, имеющей передаточную функцию W,, (р) , можно получить из формы переходной функции, имеющей передаточную функцию J(/oi (р) .(р), изменяя ее соответствующими добавками. Но поскольку коэффициенты А и получены из коэффициентов н t)j применением одного и того же масштабирования, постольку можно теперь масштаб времени определить по передаточной функции (/Q (р) для апериодической переходной функции и по передаточной функции Wjt (р) для колебательной переходной функции. Остановимся на определении масштаба времени, когда переходная функция апериодическая. При правильно выбранном масштабе времени коэффициенты должны быть меньше 1 и, следовательно, на коэффициент Д передаточной функции (/о((р) необходиМО наложить -то же условие А.) 1. Это условие выполняется при различных масштабах времени, значит на коэффициенты К накладывается лишь требование, чтобы при постоянном-интервале i 1 они давали экспоненту. Так как форма экспоненты одинакова, убедимся, что коэффициенты К дают экспоненты на одном из масштабов. Наиболее удобным для расчетов является масштаб времени, при котором Ak-i 0,5. В этом случае К 0,5 p(-Q,7i)- есть экспонента. Рассчитанные значения переходной Функции (обозначенные точками) при Л 0,5 лежат на точном ее графике (обозначенном сплошной линией) и представлены на фИг.З. Таким образом, если переходная функция - апериодическая, масштаб времени выбирают равным MO -g-. Для определения масштаба времени по коэффициентам передаточной функции Уц (р) найдем связь между коэффициентами А-1 и AT.- Поскольку форма кривой переходной функции не зависит от масштаба времени, для ее характеристики достаточно назвать какой-нибудь один параметр, не связанный со временем, например перерегулирование ta или один из коэффициентов А или Следовательно, между коэффициентами А-у и Ag должна существовать связь, т.е. один из них должен выражаться через другой и, в свою очередь,, перерегулирование, должно выражаться через один из этих коэффициентов. Эта связь + Д2 1 подсказана первым столбцом таблицы, приведенной на фиг.4, из которой следует, что достаточно назвать один из ее параметров, чтобы форма переходной функции системы, имеющей передаточную функцию WK(P) была определена. На фиг.5 по данным таблицы построена зависимость -Vi-lAi), которой следует, что эта зависимость является линейной и что коэффициенты А
и / , связанные равенством
-, + V
1, обеспечивают получение формы кривой переходной функции во всем возможном диапазоне перерегулирова,ния .
Решая уравнение .
.получим масштаб времени
М -- 17 2с( Vfe)-al
для расчета колебательной переходно функции. На фиг.З представлены дискретные значения функции - при
выбранных коэффициентах A-j . (обозначены трчками, удовлетворяющих равенству A-J+ . 1 которые лежат на точном графике этой переходной функции (обозначенной сплошной линией).
В качестве заключительного примера на фиг.6 приведены точная Форма кривой переходной функции {сплошная линия), соответствующая передаточной функции
-( -«-олер о,о45р
Ч(р)-U-1,05р-Ю,,ЪУ7р
и дискретные функции , рассчита ,ные при различных масштабах времени При масштабе времени М 0,667, рассчитанном по формуле при AI+ А2.
М С(. 1,
передаточная функция принимает вид
О,02р I407p+0,,1p
а коэффициент К принимает значения ,2, ,14; К, -0,058,К 0,021; kf 0,018} К(, 0,0007, т.е. точки дискретной функции об разуют график переходной функции
v(-t)Предложенная ЭКВМ позволяет производить расчеты линейных дифференциальных уравнений любого порядка, записанных в виде операторного изображения Лапласа-Карсона и производить анализ и синтез передаточных функций в процессе проектирования и испытания линейных динамических систем.
Формула изобретения
Электронная клавишная вычислительная машина, содержащая блок клавиатуры, блок записи чисел, блок хранения знаков, буферный накопитель, блок управления, память и арифметический блок, причем первый и второй выходы блока клавиатуры соединены соответственно с первыми входами блока записи чисел и блока управления, выход которого соединен с управляющими входами блока записи чисел, буферного накопителя, памяти, блока хранения знака и ариЛметичесoкого блока, выход блока записи чисел соединен с первым информационным входом буферного накопителя, первый выход арифметического блока соединен с информационным входом
5 памяти, отличающаяся тем, что, с целью расширения класса решаемых, задач, она содержит блок вычисления масштаба, блок возведения в степень, блок умножения на масштабные коэффициенты, блок вычис
Q ления коэффициентов, деши ратор дисекретности, дешифратор значений , функций и светодиодную матрицу, причем выход блока записи чисел соединен с первыми входами блока вычисле5ния масштаба и блока умножения на масштабные коэффициенты, выход которого через блок вычисления коэффициентов соединен со вторым информационным входом буферного накопителя,
0 выход которого соединен с первым входом арифметического блока, второй вход которого соединен с выходом блока хранения знаков, второй выход арифметического блока, сигнальные
5 выходы блока вычисления масштаба, блока возведения в степень, блока умножения на масштабные коэффициенты и буферного накопителя соединены с соответствующим входом блока управле0ния, выход которого соединен с управляющими входами дешифратора дискретности и дешифратора значений функции, информационные входы которых соединены с соответствующими выходами памяти, а выходы - соответственно со
5 входами столбцов и строк светодиодной матрицы, информационный выход блока вычисления масштаба соединен со входом блока возведения в степень, выход которого соединен с информаци0онным входом блока умножения на масштабные коэффициенты.
Источники информации, принятые во внимание при экспертизе
5 кл.С 06 F 15/02, опублик. 1976,
фу2.5
Авторы
Даты
1980-12-07—Публикация
1978-05-10—Подача