1
Изобретение относится к информационно-измерительной и вычислительной технике и может быть использовано для вычисления спектра Фурье и спекура в базисе кусочно-линейных треугольных функций, являющихся первообразными от. функций Уолта.
Известно устройство для вычисления спектра Фурье-, использующее обработку комплексных чисел, и, в частности, умножение одного комплексного числа на другое 1.
Однако это отрицательно сказывается на скорости вычисления спектральных коэффициентов.
Известно устройство содержащее аналого-цифровой преобразователь (АЦП), Цифровой сигнальный процессор Уолша, первое и второе запоминающее устройство СЗУ), арифметическое устройство (АУ) и постоянное запоминающее устройство (пЗУ). Выход АЦП соединен с входом цифрового сигнального процессора Уолша, выход которого соединен с входом первого ЗУ. Выход этого ЗУ и выход ПЗУ соединены соответственно с первым и с вторым входом АУ, выход которого соединен с входом второгО ЗУ. Аналоговый сигнал, подаваел-ый на вход АЦП,
квантуется во времени. Значе-.ния 2 дискретных, сигналов в цифровой форме поступают на вход цифрового сигнального процессора Уолша, который по этим значениям вычислу:ет спектр Уолша. Вычисленные 2 спектральных коэффициентов поступают на хранение в первое ЗУ. Затем коэффицие-нты спектра Уолша преобразуются в коэф0фициенты спектра Фурье путем умножения коэффициентов спектра Уолша на специальную матрицу преобразования спектров, элементы которой хранятся в ПЗУ. Полученные таким образом 2 коэффициентов спектра Фурье отправ.ляются на хранение во второе ЗУ 2. Недостатком этого устройства явля ется низкая точность вычисления спектра Фурье, обусловленная анали0тическими свойствами кусочно-постоянных функций Уолша. Вычисление спектра Уолша на основе преобразования Уолша-Фурье связано с кусочно-постоянной интерполяцией входного сиг5нала конечной суммы Уолша. Поэтому для достижения требуемой точности вычисления спектра Фурье приходится уменьшать шаг квантования и получать большое число, отсчетов входного сиг0нала для вычисления спектра Уолша, что приводит к снижению быстродейст вия всего анализатора спектра Фурье Цель изобретения - увеличение точ ности вычисления спектра Фурье. Поставленная цель достигается тем что в анализатор спектра Фурье, содержащий аналого-цифровой преобразо ватель , вход которого является входом анализатора, устройство вычисления спектра Уолта, выход которого соединен с первым входом первого арифметического блока, выход которо го подключен ко входу второго блока памяти, а второй вход первого арифметического блока соединен с выходом блока постоянной памяти, введен второй арифметический блок, вход ко торого . соединен с выходом аналогоцифрового преобразователя, а выход второго арифметического блока соединен со входом устройства вычисления спект.ра Уолша. В предлагаемом устройстве промех уточной спектр вычисляется не в базисе кусочно-постоянных функций Уолша, а в базисе кусочно-линейных функций, которые являются первообразными от функций Уолша.. Вычисление такого спектра можно производить по алгоритму быст рого преобразования Уолша. Рассмотрим систему кусочно-линеч ных треугольных функций М( х), по лученных путем интегрирования функци Уолша оо( м/м (, (1) где оС 0,1,2,... N , N - 2 - 1 , п наивысил : порядок данной совокупности фун .ИИ Уолша. Функции (l) образуют ПС 1ую систему линейнонезависимых фу1 ций в пространстве С непрерывных рунгций, т.е. являются в этом пространстве базисом. Рассмотрим непрерывную на 10,11 функцию д(х), не имеющую постоянной составляющей д(0)0. Любую непрерывную функцию можно представить в виде (х)- (x-)) + f((x)), где д(х) не имеет постоянной составляющей. В дальнейшем это ограничение на исходную функцию будет снято Вычислим для функции д(х) правые односторонние конечно-разностные отношения на множестве равноотстоящих значений аргумента х - ih при ,2, . . . , h 2 Г (.J-4;l i)2.((x,,)-c(V (Z) Применим к полученным отсчетам у преобразование Уолша, которое обычно задается с помощью формул
V EW -Et 5 lV
(3)
с ci.-wCx).
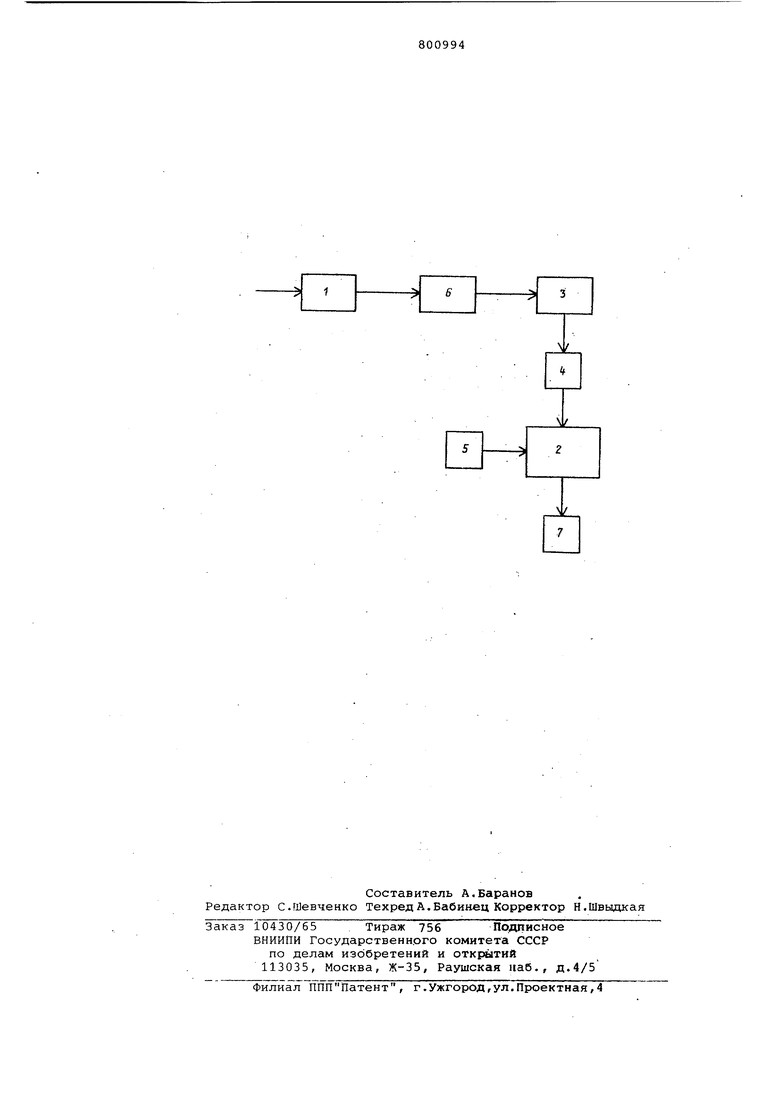
1 ,-0 d- dНапример, для функции g(х)siп ОГх/2) на интервале ОД при участках интерполяции максимальная ошибка при кусочно-линейной аппроксимации будет в Т 4-1282/;1Гг:: 326 раз Рассмотрим выражение для конечной суммы S(x), образованной из приведений коэффициентов aj преобразования (3) и куоочно---линейных функций N S.(5) г; а ул(х) . . п cL ci. Для некоторой точки на основании определения (1) и равномерной сходимости ряда Уолша имеем S (х.)-2а, w(t)clt Б a.a(t)dt--tQ (i)At, ii.-,o Разобьем интервал Го,х. интегрирования на i равных частей. На каждом таком интервале ,- где ,1,..., i-1, значение конечной суммы Qy(x) Уолша является постоянным числом равным у. . Поэтому )i )-c(v.1 Таким образом конечная сумма S| (х) ряда по функциям (к) в произвольной точке совпадает с значением исходной функции д(х) в этой же точке или, другими словами, сумма S(x) дает интерполяцию произвольной функции д(х) в базисе функций М(х) достаточно применить алгоритм быстрого преобразования Уолша к разностям g ()-д (х ) исходной функции, так как множитель 2 в выражении (2 ) сокращается благодаря множителю 2 у спектрального коэффициента Уолша. Устраним теперь ограничение g (, введенное выше. Для этого заметим, что операция (2) над произвольной функцией д(х) с д(0) автоматически исключает постоянную составляющую из полученной функции у . Введенная новая базисная система С1) дополнена внесистемной функцией Мд;,(х)1, коэффициент при которой С QQ г eg (0) для произвольной функции не может бысть вычислен по указанной методике. Погрешность при кусочно-постоянной интерполяции равна Е ill SUP хеСо,-1 а при кусочно-линейной интерполяции равна ,j-2n р )| & хем ТакимОбразом, выигрыш, получаемый при использовании кусочно-линейной аппроксимации, оценивается выражением „ SuPiq;(x)l Т..4-2 Ej ,-1 SuPK(x)l меньше, чем соответствующая ош при кусочно-постоянной интерполяц в базисе функций Уолша. Установим связь между спектрам произвольной функции д(х), получ ными в базисе тригонометрических функций Сбазис Фурье и в базисе сочно-линейных функций М|,(х). Известно, что произвольный си д(х) X 6 Го, 1 с конечной энергие можно представить на зтом интерв в виде ряда Фурье C W--CQ+Vi ,5in(2kJrx)+C,() с коэффициентами V 5с(хШ О C.,,.,-V2 с(х)8,п(ак5ГШ, C,,(.(iK5TKUx. С другой стороны ст(х)с S a.tA.lX),( dL-00 где коэффициенты а определяются (3).Подставляя (6) в (5), получае N С 01. 5,(X)d. О dL-oo С J Oi, f,(W(Ji)d:f. l L-00 С -Vi Г. a, N,(x)co5(2.Kjrx}ci-). ( ,„ --n. El - ак V oo--o U.Kj -nn - i dl Если ввести Матричную форму соотн шения спектров, обозначив °- - е-оо,0,..., е tg J .где Vg(x)oos(2 KiTxjdv , J Vg Cx) sinUK3rx)dx , m-2K+-i , 0I4 --0, i: TO C BA.. В известном анализаторе вычис ние спектра Фурье выполняется ана логичным способом: полученный на первом этапе спектр Уолша умножае ся- на специальную матрицу преобра зования спектров. Элементый этой матрицы являются ядрами Фурье соо ветствующих функций Уолша. В предлагаемом анализаторе век С спектральных коэффициентов Фурь .находится путем перемножения вект ра А коэффициентов разложения исх ного аналогового сигнала в базисе кусочно-линейных функций м(х) на специальную матрицу В преобразования спектров, элементами которой являются ядра Фурье соответствующих кусочно-линейных функций Mj(x) . ila чертеже изображен анализатор спектра Фурье. Анализатор содержит аналого-цифровой преобразователь 1, первый арифметический блок 2, устройство 3 вычисления спектра Уолша (цифровой сигнальный процессор Уолша) первый блок 4 памяти (с произвольной выборкой) , блок 5 ПОСТОЯННОЙ памяти, второй арифметический блок б, второй блок 7 памяти (с произвольной выборкой) . Выход аналого-цифрового преобразователя 1 соединен со входом блокг б, выход которого соединен со входом цифрового сигнального процессора 3 Уолша, выход которого соединен со входом блока 4. Его выход и выход блока 5 соединены со входами блока 2, выход которого соединен со входом блока 7 . Аналого-цифровой преобразователь выполняет квантоваЕше входного аналогового сигнала во времени и вырабатывает соответствующие цифровые коды. Второй арифметический блок 6 вычисления разностей вырабатывает значения в цифровой форме. В качестве такого блока может быть использован обычный cyb-wiaTop. Устройство для вычисления спектра Уолша предназначено для вычисления спектральных коэффициентов в базисе Уолша от функции, дискретные значения которой поступают на вход процессора. Первый арифметический блок предназ- . начен для выполнени я операции перс- множения вектора на матрицу, которая осуществляется с помощью устройства умножения и накапливающего сумматораВ блоке 5 хранятся коэффициенты матрицы В преобразования спектров, предварительно вычисленные и записанные в это устройство. Блоки 4 и 7 предназначены для хранения вычисленных коэффициентов Уолша и Фурье соответственно. Кроме того, первый блок памяти играет роль буфера между устройством вычисления спектра Уолша и арифметическим устройством, позволяя выполнять преобразование Уолша в устройстве и перемножение вектора на матрицу в арифметическом блоке независимо друг от друга. Анализатор работает следующим образом. На вход аналого-цифрового преобразователя поступает аналоговый входной сигнал. Преобразователь 1 квантует сигнал во времени и последовательно во времени передает цифровые значения входного сигнала на вход
блока 6,который выполняет вычисление разностей уГ-с,;,) - у (.).
Получаемые разности последовательно передаются с.выхода блока 6 на вход устройства 3 вычисления спектра Уолша, где они располагаются в памяти процессора. После окончания вычисления всех разностей устройство 3 начинает -работу и по алгоритму быстрого преобразования Уолша вычисляет вектор спектральных коэффициентов. При этом предполагается, что устройство 3 имеет необходимую для организации итерационного вычислительного процесса память.
Вычисленые устройством 3 коэффициенты поступают на хранение в блок 4. Таким образом память процессора освобождается и он может начать работу по обработке следующей выборки..
блок 2 производит вычисление спектральных клэффициентов Фурье путем перемножения вектора коэффициентов Уолша, находящегося в блоке 4t и специальной матрицы преобразования . спекторов , элементы которой наводятся в блоке 5.
Коэффициенты спектра Фурье по мере вычисления их блоком 2 заносятся Ё блок 7 памяти. Понятно, что при надлежащей балансировке скорости работы устройства 3 и блока 2 обеспечивается непрерывная циклическая работа предлагаемой схемы анализатора спектра Фурье.
Таким образом в предлагаемом анализаторе по сравнению с известным сохраняется основная идея метода вычисления спектра Фурье: выполнение предварительного спектрального преобразования Уолша, которое-оперирует с вещественными числами и характеризуется значительной скоростью и отсутствием избыточности, и затем осуществление перехода к искомому спектру Фурье с помощью.выполнения матричной операции. Однако за счет незначительного усложнения известной, схемы - введения второго арифметич ского блока - удалось, практически не снижая быстродействия устройства Б целом, значительно уменьшить погрешность вычисления спектра Фурье, благодаря введению специальной системы кусочно-линейных базисных функций, которые связаны с функциями Уолша -линейным интегральным оператором. Количественная оценка степени выиграша дается-формулой (4).
Моделирование работы анализатора 0 на ЦВМ для ряда аналоговых сигналов показало, что относительная ошибка вычисления дискретного спектра Фурье в несколько сот раз меньше ошибки, получаемой при использовании БНФ 5 при одинаковом объеме выборки.
Формула
изобретения
Q Анализатор спектра Фурье содержащий аналого-цифровой преобразователь, вход которого является входом анализатора, устройство вычисления спектра Уолша, выход которого соединен с первым входом первого арифметического блока-, выход которого подключен ко входу второго блока памяти, а второй вход первого арифметического блока соединен с .выходом . блока постоянной памяти, о т л и0 чающийся тем, что, с целью повышения точности вычисления спектра, в него введен второй арифметический блок,.вход которого соединен с выходом аналого-цифрового
5 преобразователя, а выход второго арифметического блока соединен со входом устройства вычисления спектра Уолша.
Источники информации, принятые во внимание при экспертизе
1.Авторское свидетельство СССР № 598082, кл. G 06 F 15/3, 1976.
a.Kitai R, Т., Vaila F, Usimcj oi ..Essor -in d WaEsh-Kcuurier Spectv-aS. anaSvier. IEEE,Transactions on Con-ipoters, 1976,/ipr-i ,p, 27-32 (ПРОТОТИП).



| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для управления динамическими испытаниями | 1986 |
|
SU1361504A1 |
| Анализатор спектра Фурье | 1984 |
|
SU1238102A1 |
| Цифровой анализатор спектра по функциям уолша | 1975 |
|
SU636554A1 |
| Цифровой анализатор спектра в ортогональном базисе | 1983 |
|
SU1124326A1 |
| Способ имитации сигнально-помеховой обстановки | 2023 |
|
RU2818373C1 |
| Устройство для выполнения преобразования Фурье | 1987 |
|
SU1429125A1 |
| Устройство ортогонального преобразования по Уолшу | 1980 |
|
SU922721A2 |
| Цифровой анализатор энергетического спектра | 1978 |
|
SU769443A1 |
| Анализатор спектра случайныхпРОцЕССОВ | 1979 |
|
SU838600A1 |
| Цифровой анализатор спектра | 1979 |
|
SU798615A1 |


Авторы
Даты
1981-01-30—Публикация
1979-04-02—Подача