Изобретение относится к области радиотехники и может быть использовано при полунатурных испытаниях радиотехнических средств (РТС), а также в их аппаратуре имитации и тренажа для имитации сигнально-помеховой обстановки, функционально-диагностического контроля и тренажа расчетов.
Современных РТС, способны обнаруживать и сопровождать воздушные объекты в различных климатических условиях, в стационарном и динамическом состояниях при воздействии вибраций и качек, в широких диапазонах по высоте, азимуту и скорости, в сложной активной и пассивной помеховой обстановке, включающей отражение зондирующего сигнала от различного типа подстилающих поверхностей и гидрометеоров. При этом возможна многоканальная работа как по одиночным объектам, так и по групповым целям. Вследствие указанных факторов к РТС предъявляются повышенные требования по точности и быстродействию. Для их удовлетворения необходим комплекс тестовых моделей сигналов внешней среды, обеспечивающих адекватное моделирование режимов функционирования РТС и строящихся на основе известных физических законов и математических преобразований, традиционно применяемых в цифровой обработке сигналов, а также данных натурных экспериментов. Для формирования комплекса тестирующих процессов применяются модели и алгоритмы имитации детерминированных и случайных сигналов.
Многие из существующих моделей и алгоритмов не обеспечивают реализацию процессов с энергетическими характеристиками произвольной формы, в том числе полученными экспериментально. В частности, корреляционные функции и функции спектральной плотности мощности (дисперсии) таких случайных процессов могут содержать выбросы или разрывы первого рода [1]. Те же модели и алгоритмы, которые позволяют воспроизводить подобные случайные сигналы, либо обладают высокой вычислительной сложностью, либо содержат переходные процессы. Такие недостатки известных подходов затрудняют или делают невозможным их применение для расширенной отработки режимов, существующих и перспективных РТС в реальном времени при необходимости воспроизведения сложной сигнально-помеховой обстановки.
Указанные обстоятельства приводят к снижению эффективности имитации внешней среды при полунатурных испытаниях и тестировании наземных РТС.
Известен способ имитации случайного процесса на основе разложений в тригонометрический ряд Фурье основанный на представлении сигнала суммой функций синуса и косинуса, который может быть использован для имитации воздушно-помеховой обстановки в РТС и принятый в качестве прототипа [2 с. 292-298]. Он состоит из двух этапов. Его суть заключается в следующем:
1. Этап предварительной настройки, включающий:
- ввод характеристик воспроизводимого сигнала;
- настройку точности имитации случайного процесса, регулируемой числом N его отсчетов, выбор или расчет параметров имитации;
- расчет тригонометрических коэффициентов (спектральных коэффициентов в тригонометрическом базисе);
2. Этап восстановления сигнала из спектра.
В качестве недостатков рассмотренного прототипа можно указать следующее:
1. Способ требует выполнения N2 операций сложения и умножения и 2N2+N ячеек памяти для хранения значений дисперсий и тригонометрических функций, а также затраты на формирование N случайных величин, что обуславливает большие затраты вычислительных ресурсов.
2. Невозможность имитации сигналов, задаваемых функций спектральной плотности (ФСП), автокорреляционных функций (АКФ), с выбросами и/или разрывами I рода.
3. Длительное время имитации процессов из-за присущего данному способу большого числа арифметических операций.
Техническим результатом настоящего изобретения является возможность имитации сигналов, задаваемых ФСП (АКФ), с сохранением точности имитации в жестком модельном времени РТС и уменьшение вычислительной сложности алгоритмов имитации.
Технический результат достигается тем, что в способе имитации сигнально-помеховой обстановки, заключающемся в предварительной настройке, включающей ввод таблично заданной энергетической характеристики воспроизводимого сигнала либо задание в программе выражения, соответствующего ее дискретизированному аналитическому представлению, настройку точности имитации сигнала, регулируемой числом N его отсчетов, выбор или расчет параметров имитации, расчет тригонометрических коэффициентов и непосредственную имитацию сигнала, включающую восстановление сигнала из спектра, согласно изобретения, при предварительной настройке после расчета тригонометрических коэффициентов, производится расчет элементов ядра Фурье оператора взаимопреобразования спектров между базисами Фурье и Уолша-Пэли, выделение в этом ядре независимых групп тригонометрических коэффициентов, преобразование спектра в тригонометрическом базисе в спектр в базисе Уолша-Пэли путем расчета случайных коэффициентов Уолша-Пэли, а при непосредственной имитации производится восстановление сигнала из спектра путем суммирования произведений готовых погрупповых тригонометрических коэффициентов на погрупповые значения случайных коэффициентов Уолша-Пэли.
Физическая суть предлагаемого способа заключается в следующем. На первом этапе осуществляется предварительная настройка, которая включает в себя:
Ввод исходных данных, таблично заданных энергетических характеристики сигнала (ФСПД, АКФ) либо задание в программе выражения, соответствующего ее дискретизированному аналитическому представлению (таблица 1).
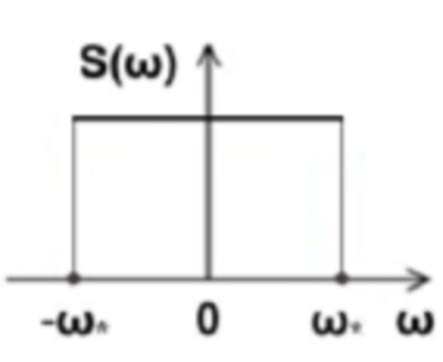
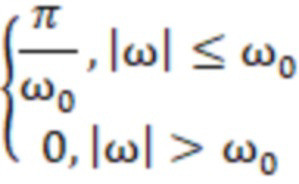

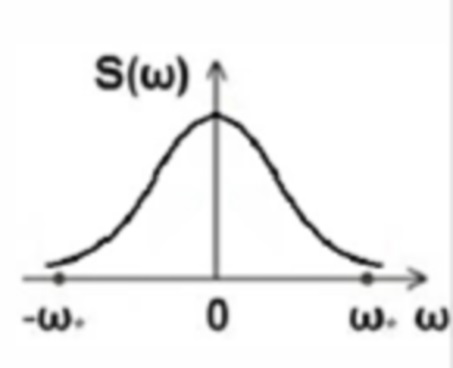
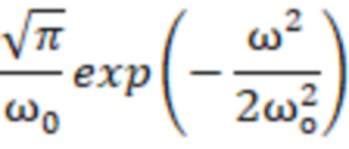
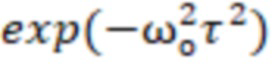
«треугольная»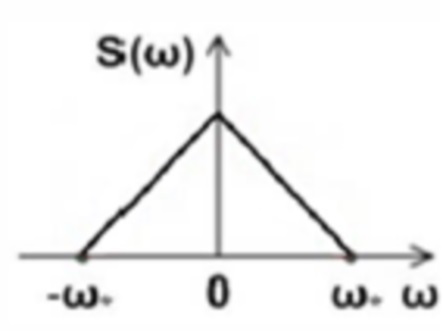


где S (ω) - функция спектральной плотности дисперсии (ФСПД);
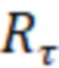 - корреляционная функция;
- корреляционная функция;
τ - время;
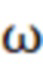 - частота реализации.
- частота реализации.
Далее производится настройка точности имитации сигнала, регулируемой числом N его отсчетов, напрямую влияющее на точность имитации.
Далее производится выбор или расчет параметров имитации в зависимости от видов имитируемых процессов, используемого для имитации алгоритма:
n - разрядность представления аргумента и номера базисной функции;
T - время имитации;
Δtk - шаг дискретизации по времени;
N - число реализаций сигнала (отсчетов);
 - дисперсия;
- дисперсия;
ωс - частота среза;
для таблично заданной исходной АКФ: ввод массива ее дискретных значений N.
Далее производится расчет тригонометрических коэффициентов:
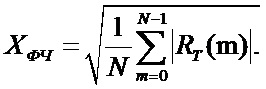 (1)
(1)
где XФЧ (k) - тригонометрические спектральные коэффициенты, рассчитанные по дискретной ФСПД или дискретной АКФ;
RT(m) - теоретическая АКФ.
Спектры одного и того же сигнала, представленного в общем функциональном пространстве разложениями в различных базисных системах, всегда связаны между собой линейным оператором преобразования, который полностью определяется своим ядром Фурье [1]. Поэтому далее производится расчет элементов ядра Фурье (ФЧ,ФН) производится на основе расчета тригонометрического спектра Фурье:
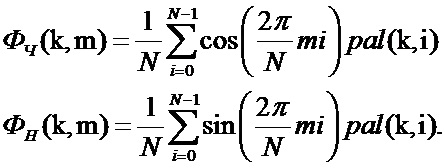 (2)
(2)
где pal - функция Уолша-Пэли.
Для каждого i-го отсчета дискретного случайного сигнала по алгоритму требуется вычисление ряда, число элементов которого зависит от числа групп n+1, которое логарифмически меньше N;
Тригонометрический спектр, является составным и представляет собой чередование четных ФЧ (косинусных) и нечетных ФН (синусных) составляющих. Элементы ядра Фурье, оператора преобразования тригонометрического спектра в спектр Уолша - Пэли (pal), также разделяются на четные и нечетные.
Поскольку мощность сигнала равна сумме мощностей его проекций [1, 3], то правильность осуществленных спектральных преобразований можно проверить с помощью равенства Парсеваля. Равенство выражает квадрат нормы элемента в таком пространстве через квадраты модулей коэффициентов Фурье этого элемента в заданной ортогональной системе.
Так как выделенные группы спектральных коэффициентов независимые, то в пределах каждой группы мощность сигнала как в тригонометрическом базисе, так и в базисе Уолша - Пэли одинакова. Следовательно, равенства Парсеваля можно записать по группам и соответственно выделить независимые группы спектральных коэффициентов:
- для группы 1: 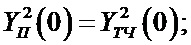
- для группы 2: 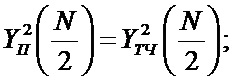
- для группы с номером λ, λ=3,4,…,n+1:
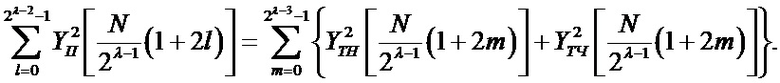
l=0,1,…,2λ-2-1
где YП - случайный спектр Уолша-Пэли YТЧ четные и YТН нечётные.
Эти равенства говорят о том, что распределение мощности сигнала по группам коэффициентов одинаково при представлении сигнала в тригонометрическом базисе и в базисе Уолша - Пэли.
Расчет по приведенным выше формулам позволяет получить ядро Фурье для любых N=2n.
Расчеты показали, что значительная часть элементов матрицы ядра Фурье равна нулю. Это имеет место и в общем случае, при произвольных значениях N. Для сокращения вычислительной сложности процесса преобразования спектров необходимо избежать выполнения арифметических операций, совершаемых впустую, т.е. над нулевыми элементами. Кроме того, тривиальное умножение на элемент, равный ±1, также не должно выполняться, а лишь приводить к смене знака операнда. При программной реализации алгоритмов имитации такие ситуации легко отслеживаются и дают дополнительную экономию времени преобразований.
Далее производится преобразование спектра в тригонометрическом базисе, в спектр в базисе Уолша-Пэли, путем расчета случайных коэффициентов Уолша-Пэли:
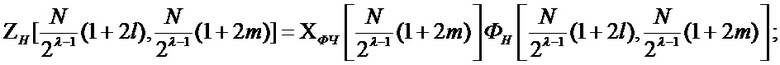
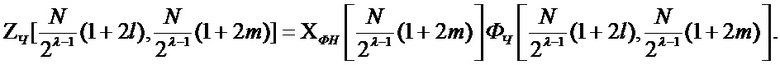 (3)
(3)
Из выражения (3) видно, что величины ZН и ZЧ, являющиеся для каждой группы λ и каждого значения индексных переменных m, l произведением соответствующих спектрального коэффициента и элемента ядра Фурье, также можно вычислить на этапе настройки, хранить в памяти ЭВМ и использовать в готовом виде на этапе непосредственного воспроизведения сигнала. В результате значительный объем вычислительных операций будет отнесен к этапу настройки, существенно сокращая вычислительную сложность этапа непосредственной имитации сигнала.
Далее осуществляется непосредственно имитация сигнала, включающая восстановление сигнала из спектра с помощью имитации сигнала в базисе Уолша-Пэли. Он представляется следующей формулой восстановления сигнала из спектра в базисной системе Уолша - Пэли [3]:
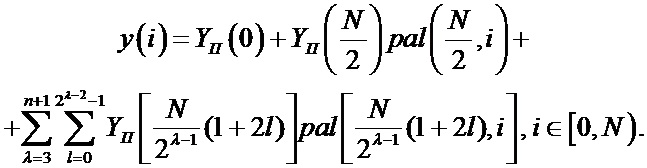 (4)
(4)
Этап непосредственной имитации сводится в таком случае к суммированию произведений готовых погрупповых тригонометрических коэффициентов YП на погрупповые значения базисных функций Уолша - Пэли.
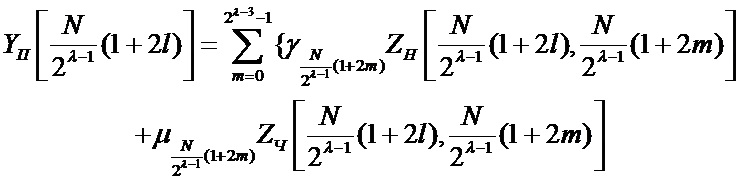 , (5)
, (5)
λ=3,4,…,n+1, l=0,1,…,2λ-2-1.
Операции умножения на этапе непосредственной имитации полностью исключены. Случайное изменение знаков обеспечивается теми же ранее введенными некоррелированными случайными величинами μ и γ с введенной для них обобщенной индикацией:  и
и  , где выражение (1+2m) определяет номер величины, а выражение N/(2λ-1) относит ее к соответствующей группе.
, где выражение (1+2m) определяет номер величины, а выражение N/(2λ-1) относит ее к соответствующей группе.
Таким образом, за счет вынесения на этап настройки практически всех основных вычислительных операций, причем при погрупповом их выполнении, а также сокращении ряда для каждого i -го отсчета сигнала до количества членов, зависящего от числа групп, а не от числа отсчетов, суммарное число операций, выполняемых на этапе непосредственной имитации сигнала, сведено к минимуму.
Изобретение иллюстрируется следующими чертежами.
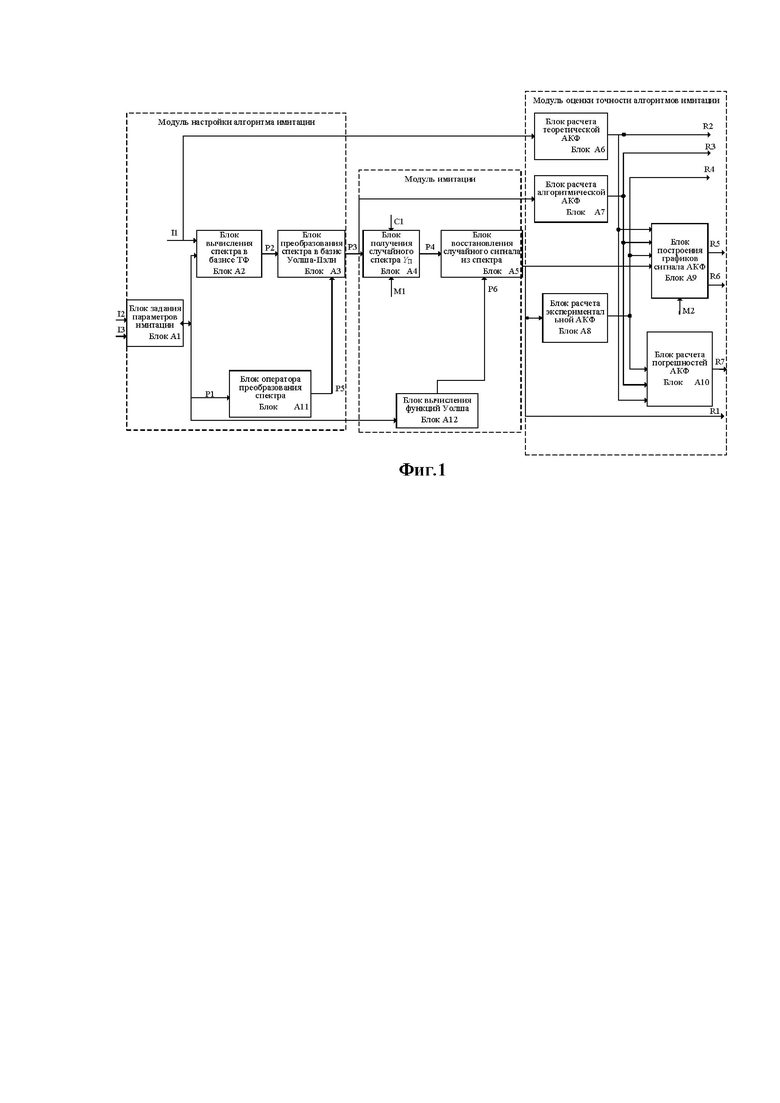
На фиг. 1 представлена блок-схема предлагаемого способа, которая включает следующие обозначения:
- А1 - Блок задания параметров имитации;
- А2 - Блок вычисления спектра в базисе тригонометрических функций (ТФ)
- А3 - Блок преобразования спектра в базис Уолша-Пэли;
- А4 - Блок получения случайного спектра;
- А5 - Блок восстановления случайного сигнала из спектра;
- А6 - Блок расчета теоретической АКФ;
- А7 - Блок расчета алгоритмической АКФ;
- А8 - Блок расчета экспериментальной АКФ;
- А9 - Блок построения графиков;
- А10 - Блок расчета погрешностей АКФ;
- А11 - Блок оператора преобразования спектра;
- А12 - Блок расчета функций Уолша;
- Р1 - порядок ядра Фурье (число отсчетов, мощность исходной и целевой систем базисных функций);
- Р2 - детерминированный спектр сигнала в базисе ТФ;
- Р3 - спектр сигнала в базисе Уолша - Пэли, полученный с помощью прямого или оптимизированного оператора преобразования спектра;
- P4 - случайный спектр сигнала в базисе Уолша - Пэли;
- P5 - уравнения преобразования спектра;
- Р6 - значения функций Уолша в упорядочении Пэли.
- I1 - энергетическая характеристика сигнала (ФСПД или АКФ) в табличном (дискретном) или аналитическом представлении;
- I2 - число отсчетов N, напрямую влияющее на точность имитации;
- I3 - вектор параметров, зависящий от задаваемых требований к имитации (T, Δtk, σc, ωс, n число реализаций сигнала).
- R1 - вектор значений воспроизведенного сигнала;
- R2 - вектор значений теоретической АКФ;
- R3 - вектор значений алгоритмической АКФ;
- R4 - вектор значений экспериментальной АКФ;
- R5 - график воспроизведенного сигнала;
- R6 - графики АКФ;
- R7 - значения погрешностей АКФ.
- M1 - датчик случайных чисел с заданным законом распределения;
- M2 - построитель графиков функций.
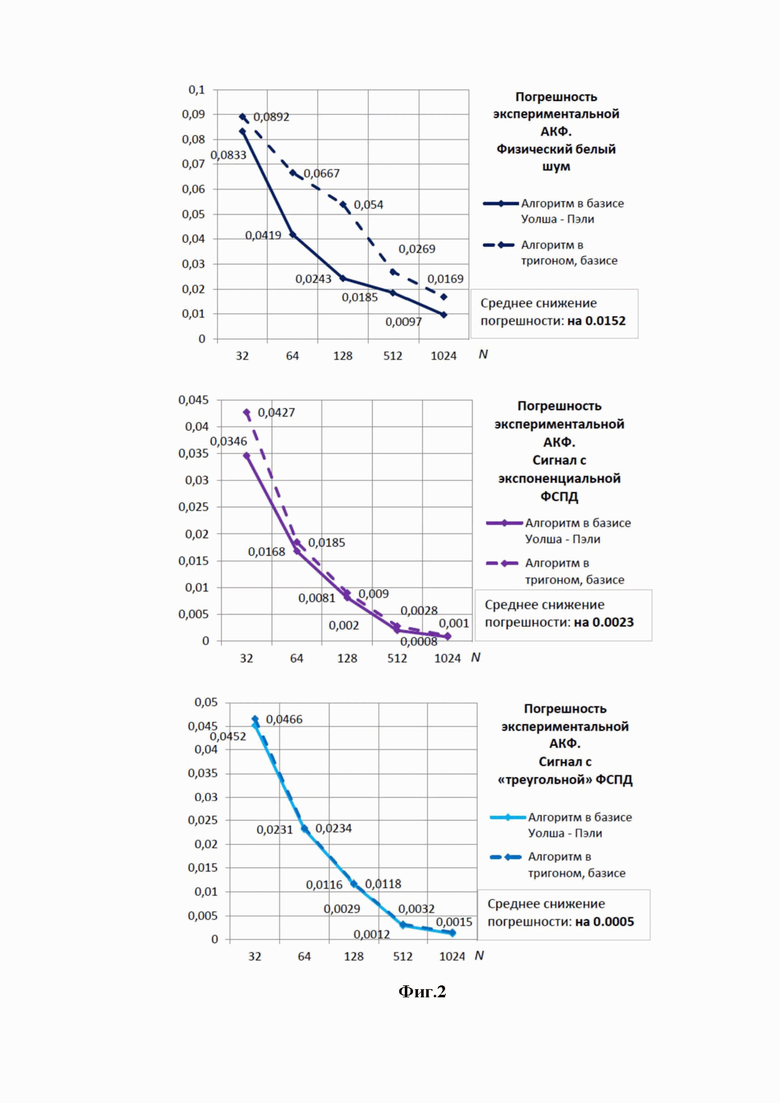
На фиг. 2 представлены графики зависимости погрешностей АКФ от числа отсчетов имитируемого сигнал физического белого шума, экспоненциальной и кусочно-линейной («треугольная»).
Реализация способа заключается в последовательном выполнении следующих операций:
1. Дискретизация заданной энергетической характеристики сигнала выполняется до начала работы, дискретные значения поступают на вход I1. Входные данные и параметры Ii, i=1,3, а также результаты моделирования Rj, j=1,7 в соответствии с выражениями (1-3). При этом блок А1 полностью реализует этап задания исходных данных и параметров имитации, а блоки А6 - А10 отвечают за оценку качества алгоритма имитации по результатам воспроизведения сигналов. Вычисление трех видов АКФ происходит в отдельных функциональных блоках А6 - А8, после чего результаты поступают в процедуры построения графиков АКФ и сигнала (блок А9) и определения погрешностей (блок А10).
2. В блоке А2 вычисляются дискретные спектральные коэффициенты в тригонометрическом базисе, затем выполняется преобразование спектра в базис Уолша - Пэли (блок А3), а прямой либо оптимизированный операторы преобразования спектра (блок А11) служат функциональным механизмом для спектрального преобразования.
3. С помощью датчика случайных чисел (механизм М1) генерируются случайные величины μ, γ имитации стационарных сигналов, формируется случайный спектр (блок А4), из которого восстанавливается случайный сигнал с помощью преобразований в базисе Уолша - Пэли (блок А5).
В результате имитационного моделирования в среде Matlab предлагаемым способом установлено, что предлагаемый способ не только не ухудшает точность воспроизведения сигналов, но и обладает несколько более высокой точностью имитации по погрешности экспериментальной АКФ.
С целью проведения вычислительного эксперимента были выбраны три аналитически задаваемые ФСПД нерационального вида и соответствующие им автокорреляционные функции: физического белого шума, экспоненциальная и кусочно-линейная («треугольная»). Данные характеристики применяются на практике, хорошо изучены [1,3] и могут служить в качестве тестовых при испытании алгоритмов имитации случайных процессов, представленными в таблице 1.
Параметры имитации физического белого шума: N=128, ωc=10π, b=0.5, σ=1. Значение дисперсии взято равным единице для удобства последующего сравнения и оценки погрешностей, получаемых АКФ имитируемых сигналов.
Параметры имитации экспоненциальной и кусочно-линейной функции N=128, ωc=10π, σ=1: Параметр дискретизации b для экспоненциальной ФСПД взят равным 0.001, для «треугольной» - 0.5.
Практическое моделирование показало, что новый разработанный алгоритм не только не ухудшает точность воспроизведения сигналов, но и обладает несколько более высокой точностью имитации по погрешности экспериментальной АКФ. На примененных ФСПД при достаточном в практических задачах числе отсчетов N=128 снижение указанной погрешности составило величину от 0.002 до 0.03. Среднее снижение погрешности при имитации на тех же ФСПД и значениях N от 32 до 1024 имеет разброс от 0.0005 до 0.0152 (Фиг. 2).
Проведенный анализ всех основных этапов имитации алгоритмов на основе Фурье и Уолша-Пэли представленный в таблице 2, показал коэффициент выигрыша по времени в среднем больше 20% (что говорит о уменьшение времени имитации сигнала), что дает возможность имитации в жестком модельном времени сигнально-помеховой обстановки РТС.
Таблица 2. Анализ всех основных этапов имитации алгоритмов на основе Фурье и Уолша-Пэли

Аналитическая оценка временной вычислительной сложности разработанного способа имитации, представленный в таблице 3, которая показала преимущество имитации в базисе Уолша - Пэли перед имитацией в базисе тригонометрических функций. По сравнению с ними вычислительная сложность алгоритмов имитации стационарных сигналов сократилась не менее чем в 1.2 раза.
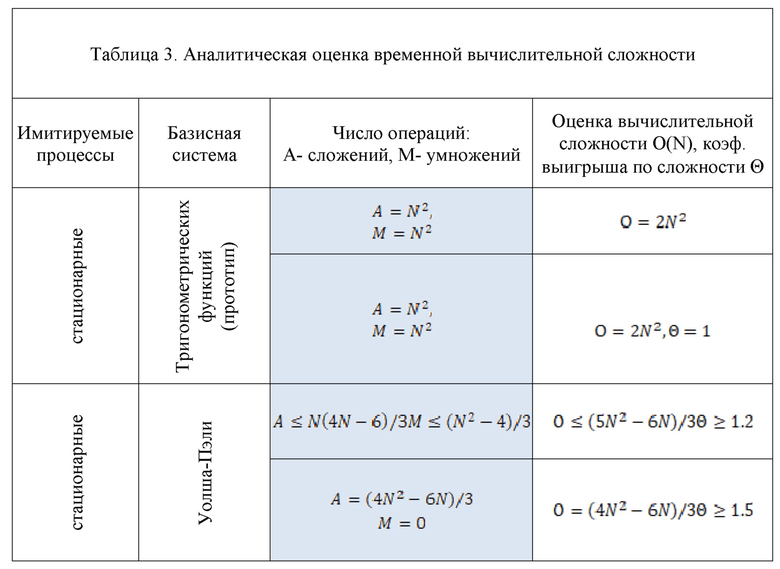
Таким образом, разработанный способ имитации сигнально-помеховой обстановки позволяет имитировать в жестком модельном времени сигнально-помеховую обстановку РТС и уменьшить вычислительную сложность алгоритмов имитации при полунатурных испытаниях.
Предлагаемый способ промышленно применим, так как основан на известных достижениях радиоэлектронной техники и не требует внесения изменений в конструкцию радиолокационного комплекса.
Список используемых источников
1. Залманзон Л.А. Преобразования Фурье, Уолша, Хаара и их применение в управлении, связи и других областях. М.: Наука. 1989. 496 с.
2. Пугачев В.С. Теория случайных функций и ее применение к задачам автоматического управления. 3-е изд., испр. М.: Физматгиз. 1962. 883 с.
3. Алгоритмы преобразования спектров в базисах Хартли и Уолша / Пролетарский А.В. [и др.] // Автоматизация. Современные технологии. М.: Изд-во «Инновационное машиностроение». 2018. Т. 72, № 10. С. 453-461.
4. Виноград С. О вычислении дискретного преобразования Фурье // Макклеллан Дж.Г., Рейдер Ч.М. Применение теории чисел в цифровой обработке сигналов. М.: Радио и связь. 1983. С. 117-136.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ обнаружения воздушных объектов при зондировании сверхкороткими радиоимпульсами | 2022 |
|
RU2791275C1 |
| Способ определения разности расстояний до постановщика многократной ответно-импульсной помехи в активно-пассивной многопозиционной радиолокационной системе | 2020 |
|
RU2745108C1 |
| Способ спектрально-корреляционного обнаружения летательных аппаратов по квазинепрерывным импульсным сигналам бортовых радиоэлектронных систем | 2021 |
|
RU2768370C1 |
| Способ высокоточной пеленгации постановщика многократной ответно-импульсной помехи | 2020 |
|
RU2740296C1 |
| Анализатор спектра фурье | 1979 |
|
SU800994A1 |
| Цифровое устройство определения спектра принимаемых сигналов с высоким разрешением по частоте | 2020 |
|
RU2756024C1 |
| Способ двойного спектрального анализа и взвешенной обработки квазинепрерывных сигналов при отсутствии априорных сведений об их параметрах | 2024 |
|
RU2838368C1 |
| Устройство для управления динамическими испытаниями | 1986 |
|
SU1361504A1 |
| Генератор случайных процессов | 1978 |
|
SU752309A1 |
| СПОСОБ ПРИЕМА OFDM СИГНАЛОВ | 2017 |
|
RU2719396C2 |
Изобретение относится к способу имитации сигнально-помеховой обстановки. Для имитации сигнально-помеховой обстановки вводят таблично заданную энергетическую характеристику воспроизводимого сигнала, или задают в программе выражение, соответствующее ее дискретизированному аналитическому представлению, настраивают точность имитации сигналов на основе числа отсчетов, выбирают и рассчитывают параметры имитации определенным образом. Обеспечивается повышение точности имитации и уменьшение вычислительной сложности алгоритмов имитации. 2 ил., 3 табл.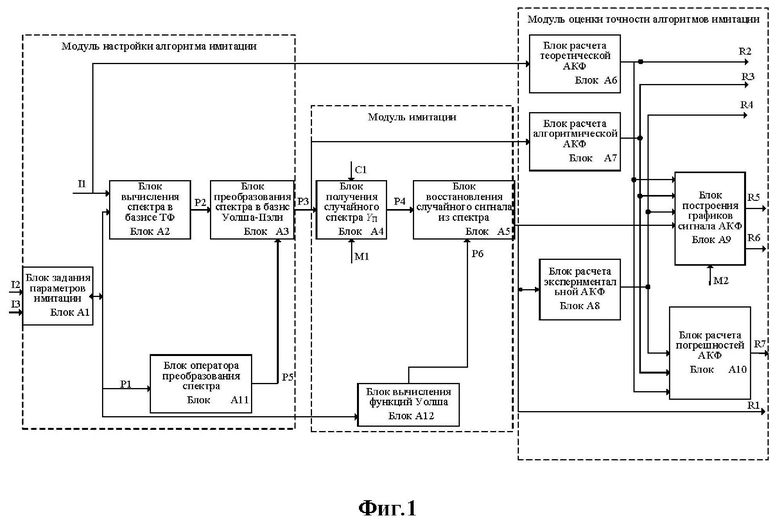
Способ имитации сигнально-помеховой обстановки, заключающийся в предварительной настройке, включающей ввод таблично заданной энергетической характеристики воспроизводимого сигнала либо задание в программе выражения, соответствующего ее дискретизированному аналитическому представлению, настройку точности имитации сигнала, регулируемой числом N его отсчетов, выбор или расчет параметров имитации, расчет тригонометрических коэффициентов и непосредственную имитацию сигнала, включающую восстановление сигнала из спектра, отличающийся тем, что при предварительной настройке после расчета тригонометрических коэффициентов производится расчет элементов ядра Фурье оператора взаимопреобразования спектров между базисами Фурье и Уолша-Пэли, выделение в этом ядре независимых групп тригонометрических коэффициентов, преобразование спектра в тригонометрическом базисе в спектр в базисе Уолша-Пэли путем расчета случайных коэффициентов Уолша-Пэли, а при непосредственной имитации производится восстановление сигнала из спектра путем суммирования произведений готовых погрупповых тригонометрических коэффициентов на погрупповые значения случайных коэффициентов Уолша-Пэли.
| В.Е.Важенин | |||
| Полунатурное моделирование бортовых радиолокационных систем, работающих по земной поверхности | |||
| Екатеринбург | |||
| Устройство для закрепления лыж на раме мотоциклов и велосипедов взамен переднего колеса | 1924 |
|
SU2015A1 |
| ИМИТАТОР ИСТОЧНИКОВ РАДИОСИГНАЛОВ | 1994 |
|
RU2094815C1 |
| Способ имитации радиосигнала | 2020 |
|
RU2747883C1 |
| Устройство полунатурного моделирования системы управления беспилотным летательным аппаратом с радиолокационным визиром | 2015 |
|
RU2629709C2 |
| CN 101382968 B, 03.11.2010 | |||
| US 20030088390 A1, 08.05.2003. | |||
Авторы
Даты
2024-05-02—Публикация
2023-09-24—Подача