(54) ЦИФРОВОЙ ГЕНЕРАТОР ОРТОГОНАЛЬНЫХ ФУНКЦИЙ


| название | год | авторы | номер документа |
|---|---|---|---|
| Цифровой генератор ортогональных функций | 1980 |
|
SU932478A2 |
| Цифровой генератор ортогональных функций | 1979 |
|
SU864274A1 |
| Цифровой генератор функций | 1984 |
|
SU1166091A1 |
| Генератор функций Хаара | 1980 |
|
SU947847A2 |
| Генератор функций хаара | 1979 |
|
SU783778A1 |
| Генератор функций хаара | 1978 |
|
SU765796A1 |
| Генератор функций Шаудера | 1987 |
|
SU1513433A1 |
| УСТРОЙСТВО ФОРМИРОВАНИЯ ФУНКЦИЙ ФАБЕРА-ШАУДЕРА | 1991 |
|
RU2025769C1 |
| Цифровой генератор функций | 1984 |
|
SU1203498A1 |
| Стохастический генератор функций Хаара | 1984 |
|
SU1233131A1 |

1
Изобретение относится к автоматике и вычислительной технике. Оно может быть использовано в аппаратуре сжатия информации при передаче данных для анализа и обработки звуковых и видеосигналов, для спектрального анализа случайных процессов и т. д.
Известен цифровой генератор ортогональных функций, содержащий счетчик, элементы И, элементы взвешивания 1.
Наиболее близким техническим решением к предлагаемому изобретению является цифровой генератор ортогональных функций, состоящий из регистров номера функции, аргумента, сдвигового регистра и элементов И.
Недостатком известных генераторов являются ограниченные функциональные возможности, поскольку они предназначены для генерирования функций какого-нибудь одного семейства (Хаара, Уолша), но не могут генерировать одновременно функций, относящихся к различным семействам, например функции Хаара и их интегральных функций, известных как функции Шаудера.
Цель изобретения - расширение функциональных возможностей цифрового генератора ортогональных функций, а именно обеспечение возможности одновременного генерирования функции Хаара и Шаудера с одинаковым номером.
Поставленная цель достигается тем, что
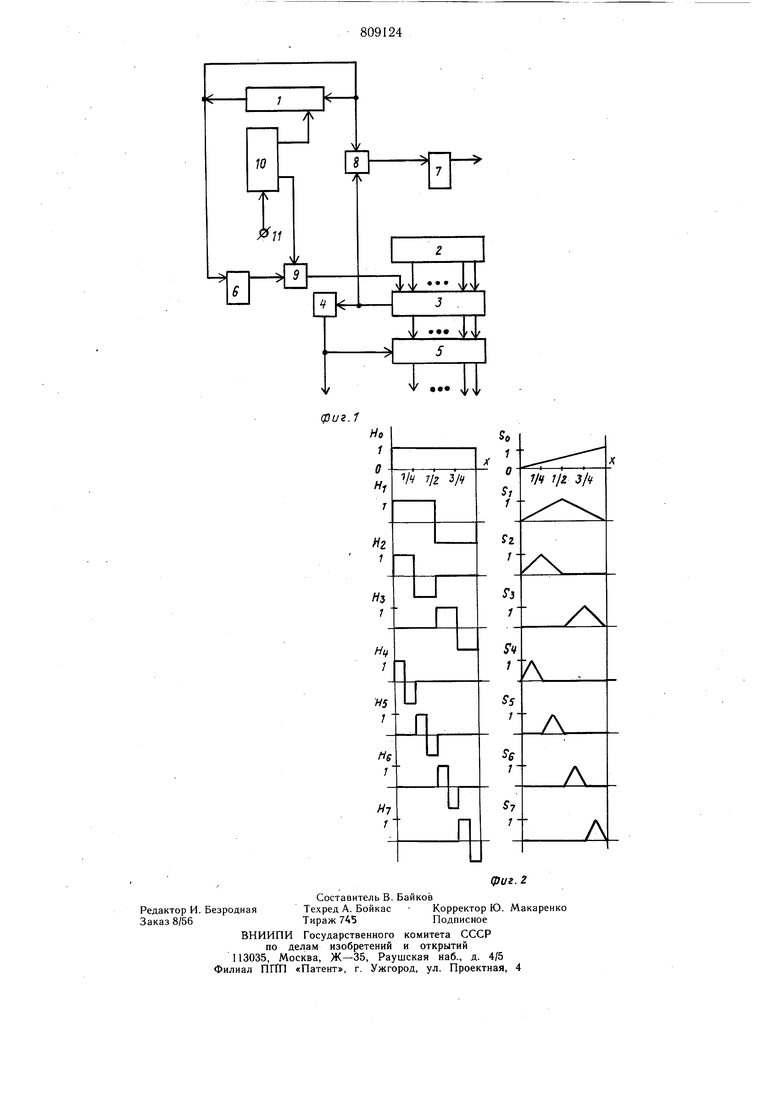
цифровой генератор ортогональных функций, содержащий кольцевой регистр сдвига номера функции, регистр аргумента, регистр сдвига, элемент И, включает дополнительно одноразрядный регистр сдвига, блок преобразования прямого кода в дополнительный, два триггера, сумматор по модулю два и блок формирования пачек импульсов, причем выход регистра сдвига номера функцииподключен к единичному входу первого триггера и первому входу сумматора по модулю два, выход которого подключен к единичному входу второго триггера, а второй вход, а также вход одноразрядного регистра - к выходу регистра сдвига, входы разрядов которого подключены к выходам одноименных разрядов регистра аргумента, а тактовый вход - к выходу элемента И, вход блока формирования пачек импульсов является тактовым входом цифрового генератора ортогональных функций, первый выход подключен к тактовому входу регистра сдвига номера функции, а второй выход -- к первому входу элемента И, второй вход которого подключен к единичному выходу первого триггера, выход одноразрядного регистра сдвига подключен к управляющему, а выходы разрядов регистра сдвига - ко входам одноименных разрядов блока преобразования прямого кода в дополнительный, выходы триггеров, одноразрядного регистра сдвига и регистра сдвига являются выходами цифрового генератора ортогональных функций. На фиг. 1 представлена функциональная схема цифрового генератора ортогональных функций; на фиг. 2 - первые семь функций Хаара и Шаудера. Цифровой генератор ортогональных функций содержит кольцевой регистр 1 сдвига номера функций,регистр аргумента 2, регистр сдвига 3, одноразрядный регистр сдвига 4, блок 5 преобразования прямого кода в дополнительный, триггеры 6 и 7, сумматор 8 по модулю два, элемент И 9, блок 10 формирования пачек импульсов, тактовый вход 11. Ненормированные, трехзначные, ортогональные функции Хаара }(} имеют опре деление: Но(х) 1, , при xeEpt. Н/)()Нр-,(х) при хбЕрГ, 0, при р - номер группы функций (порядок функции) р 1,2,...; i -номер функции в группе р (i 0,1 ... 2 -сквозной номер функцииоС tpi -двоичный отрезок , oi. - ЛЯОИЧНЫЙ ПТПРЧПК f-111-; р. pl -двоичный отрезок tpi -ДВОИЧНЫЙ отрезок причем /| pir/+/Epr /. Система треугольных функций ) (функций Шаудера) определяется следуюшим образом 2.(х- ),TtpMxetpL 2(-х),11ри U) ) ) .0, при X . Каждая система функций строится гру/ь пами, каждая из которых содержит 2 функций (р 0). Пусть в рассматриваемом устройстве нонер « кодируется целым двоичным числом Xi,o6-c(-n. аргумент х представлен двоичным кодом X ьХя1..Хи1., в котором запятая фиксируется перед крайним левым разрядом. При этом m п для того, чтобы получать значения S (х) не только в вершинах треугольников функций старшего порядка. Такой способ кодирования позволяет по номеру оС функции легко определить порядок р этой функции и ее номер i в группе. Действительно, номер разряда кода оС, в котором находится самая старшая единица, при счете справа налево и есть порядок р этой функции, а оставшийся справа от этой единицы код есть номер i этой функции в группе р. Например,для кода 000101101 номера о1 функции Hgj(x) или функции So( (х) порядок р 6, -а код номера i функции есть 01101, 13,0. Если а I старший из разрядов, принимаюших единичное значение в коде оС(т. е. q - п-р+1), тогда интервал 2pi представляется значениями х ч-г ...«.р. ...х«,(т. е. X , о(.ц, ХР-, ot), а разряды Хр, Xpti, ..., Xtrv в этом интервале позволяют определить значение функций Hpi., Spv ри -XwiCSjO) HbL + 1; Sot 0-Х Хр 1 - Hpi.-l;SpL 1-О.Хр.1...х.(3,5) За пределами интервала tpt, т. е. при (3(.1+ xi) V ( х,.) V...V( Хр.. получаем Нр;. 0, S р1 0. Генератор ортогональных функций работает следующим образом. Значение функции .НА(Х) и функции (x) вычисляются за п+1 тактов работы устройства. После окончания каждого цикла вычислений на регистре номера функции и на регистре аргумента сохраняются прежние значения номера функции и аргумента. Затем содержимое регистра номера функции увеличивается на единицу и вновь повторяется цикл вычисления очередных двух значений функций. После вычисления 2 пар значений функций Хаара и функций Шаудера можно изменить содержимое регистра аргумента и начать вычисления для этого нового значения. В исходном положении на регистре 1 устанавливается код номера функции, на регистре 2 - код аргумента, на регистре 4 и триггерах 6 и 7 - нулевой код. На вход 11 начинают поступать тактовые им.пульсы. Содержимое регистра 2 по первому тактовому импульсу переписывается в регистр 3. С первого выхода блока 10 на сдвиговый вход регистра 1 поступает серия из п импульсов, со второго выхода на вход элемента И 9 поступает серия из п + 1 импульсов. На q-OM такте первая единица кода номера функции переписывается из крайнего левого разряда регистра 1 в крайний правый разряд, а триггер 6 переводится в положение «1. Теперь управляющие импульсы со второго выхода блока 10, проходя через элемент И 9, начинают поступать на сдвиговый вход регистра 3 и вызывают сдвиг влево его содержимого. Каждый управляющий импульс вызывает поступление на входы сумматора 8 значений соответствующих разрядов кода номера функции и кода аргумента, так что в конце цикла вычислений состояние триггера 7 определяет значение левой части выражения (4). В результате сдвига кода аргумента в регистрах 3 и 4 под действием импульсов с (q+l)-ro по (пЧ-1)-ый, поступающих со второго выхода блока 10 через элемент И 9, в регистре 4 оказывается разряд хр кода аргумента, а в регистре 3 - код Х(+ X|i+t.. ..X 00...О Вычисления закончены. На выходе блока 5 в соответствии с выражениями (3) формируется значение Spi., причем выдача прямого или дополнительного кода определяется управлением с выхода регистра 4 (т. е. значением разряда хр). Значения функций Н, S определяются по таблице. БезразличноВыход блока 5 Выход блока 5 После окончания каждого цикла вычислений пары значений функций схема генератора приводится в исходное положение. Таким образом, предлагаемое устройство имеет более щирокие функциональные возможности по сравнению с известным, так как вычисляет значения кусочно-постоянных функций Хаара и кусочно-линейных функций Шаудера. Расщирение функциональных возможностей достигается незначительным усложнением схемы. При этом вычисление значений треугольных функций, имеющих значительно больщую конструктивную сложность по сравнению с кусочно-постоянными функциями Уолша, осуществляется за п + 1 тактов, что всего на один- такт больше времени вычисления значений функций Уолша. Кроме того, при увеличении длины обрабатываемых кодов номера функции и аргумента в предлагаемом устройстве увеличивается только длина соответствующих регистров, тогда как в схеме пр&тотипа увеличивается длина соответствующих регистров и количество элементов И. Формула изобретения Цифровой генератор ортогональных функций, содержащий кольцевой регистр сдвига номера функции, регистр аргумента, регистр сдвига, элемент И, отличаюш,ийся тем, что, с целью расширения функциональных возможностей цифрового генератора, состоящего в возможности одновременного генерирования функций Хаара и Шаудера с одинаковым но.мером, в него введены одноразрядный регистр сдвига, блок преобразования прямого кода в дополнительный, два триггера, сумматор по модулю два и блок формирования пачек импульсов, причемвыход регистра сдвига номера функции подключен к единичному входу первого триггера и первому входу сумматора по модулю два, выход которого подключен к единичному входу второго триггера, а второй вход и вход одноразрядного регистра подключены к выходу регистра сдвига, в.ходы разрядов которого подключены к выходам одноименных разрядов регистра аргумента, а тактовый вход - к выходу элемента И, вход блока формирования пачек и.мпульсов является тактовым входом цифрового генератора ортогональных функций, первый выход подключен к тактовому входу регистра сдвига номера функции, а второй выход - к первому входу элемента И, второй вход которого подключен к единичному выходу первого триггера, выход одноразрядного регистра сдвига подключен к управляющему, а выходы разрядов регистра сдвига - ко входам одноименных разрядов блока преобразования прямого кода в дополнительный, выходы триггеров, одноразрядного регистра сдвига и регистра сдвига являются выходами цифрового генератора ортогональных . Источники информации, принятые во внимание при экспертизе 1.Авторское свидетельство СССР № 446050, кл. G 06 F 1/02, 1972. 2.Авторское свидетельство СССР № 495658, кл. G 06 F 1/02, 1974 (прототип).
Авторы
Даты
1981-02-28—Публикация
1978-11-27—Подача