I
Изобретение относится к автоматике и вычислительной технике, может быть использовано для спектрального и корреляционного анализа случайных процессов,в аппаратуре сжатия и уплотнения информации, фильтрации, помехоустойчивого кодирования, для анализа и обработки звуковых видеосигналов.
По основному авт. св. № 809124 известен цифровой генератор ортогональных функций, содержащий кольцевой регистр сдвига номера функции, регистр аргумента, регистр сдвига, элемент И, одноразрядный регистр сдвига, блок преобразования прямого кода в дополнительный, два триггера, сумматор по модулю два и блок формирования пачек импульсов, причем .выход кольцевого регистра сдвига номера функции подключен к единичному входу первого триггера и первому входу сумматора по модулю два, выход которого
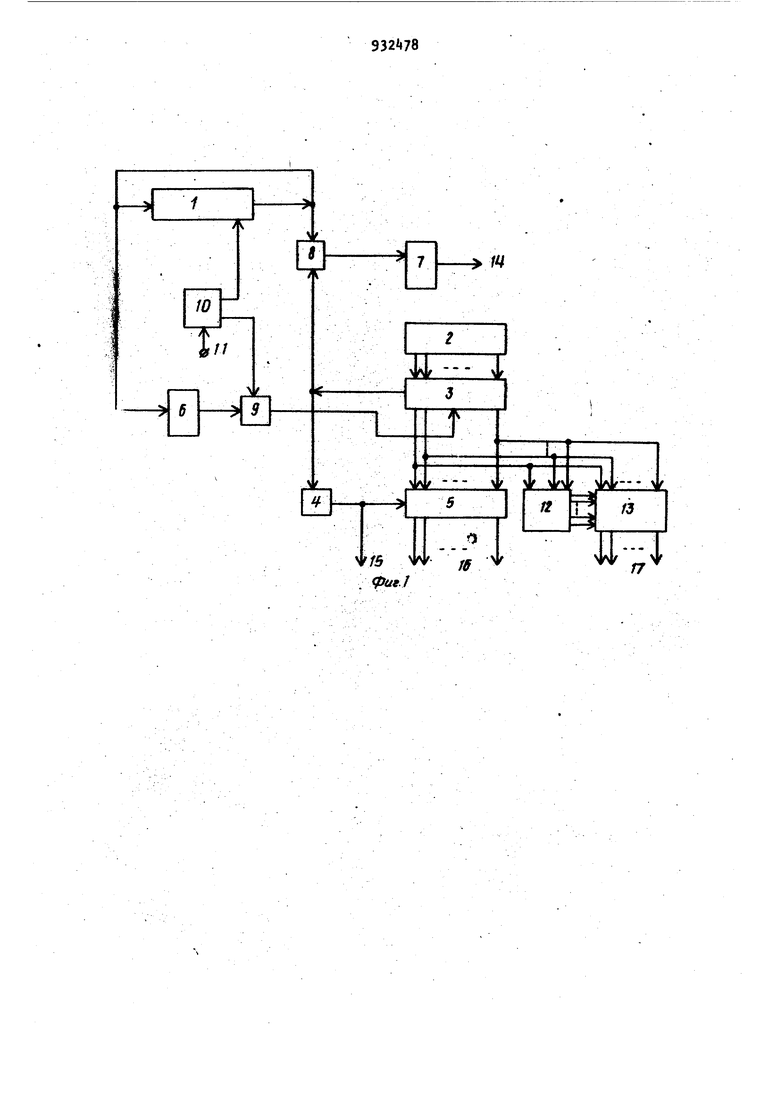
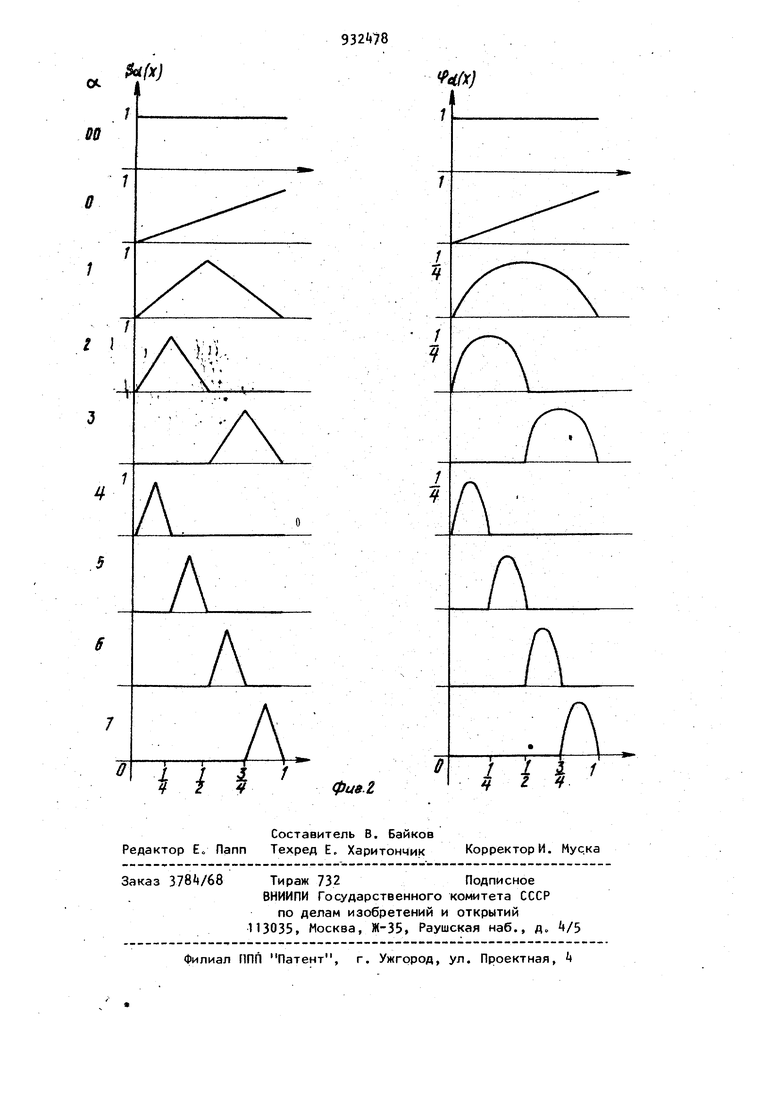
подключен к единичному входу второго триггера, а второй вход и вход одноразрядного регистра сдвига подключены к выходу регистра сдвига, входы разрядов регистра сдвига подключены к .выходам одноименных разрядов регистра аргумента, а Тактевый вход - к выходу элемента И, вход блока формирования пачек импульсов является тактовым входом генератора, первый выход подключен к тактовому входу кольцевого регистра сдвига номера функции, а второй выход к первому входу элемента И, второй вход элемента И подключен к единичному выходу первого триггера, выход одноразрядного регистра сдвига подключен к управляющему, а выходы разрядов регистра сдвига - к входам одноименных разрядов блока преобразования прямого кода в дополнительный, выходы второго триггера, одноразрядного регистра сдвига и блока преобразования прямого кода а дополнительный являются выходами генератора 1. 3932478 Недостатком известного генератора являются ограниченные функциональные возможности, так как он не может генерировать кусочно-квадратические функции.5 Цель изобретения - расширение функциональных возможностей цифрового генератора ортогональных функций, состоящее в возможности генерирования кусочно-квадратических функций. Ю Поставленная цель Достигается тем, что Цифровой генератор ортогональных функций содержит дополнительный блок преобразования прямого кода в дополнительный и множительный блок, при- 15 чем выходы разрядов регистра сдвига подключены к первой группе входов множительного блока и через дополнительный блок преобразования прямого кода в дополнительный - к второй 20 группе входов множительного блока, выходы которого являются дополнительными выходами генератора. На фиг. 1 представлена функциональная схема цифрового генератор ор-25 тогональных функций; на фиг. 2 показаны системы ортогональных функций Шаудера ($) и кусочно-квадратических функций ((,) .I Цифровой генератор ортогональных зд функций содержит кольцевой регистр 1 сдвига номера функции, регистр 2 аргумента, регистр 3 сдвига, одноразрядный регистр сдвига, блок 5 преобразования прямого кода в дополни- . тельный, триггеры 6 и 7, суммматор 8 по модулю два, элемент И 9, блок 10 формирования пачек импульсов, тактовый вход 11 генератора, дополнительный блок 12 преобразования прямого кода в дополнительный, множительный блок 13, выходы 14-17 генератора. Система ненормированных, трехзначных ортогональных функций Хаара Hi(x), генерируемых в предлагаемом генерато-, ре, определяется следующим образом: HO(X) 1; Г-«-1, при хе вр,, Н.(х)Нр. (х) J-1, при хеСр ; riIn ...., О, при хе 2р., номер группы функгде ,2N ций (порядок функций) ; Р-1 номер функции в ,1,...,2 -1 группе р; сквозной номер функции;ней фун и о пам ций фун ром р d кус вед мер лом ста при А фун для дей еди обн выч tspi - двоичный отрезок Г 1; iH .Р - ДВОИЧНЫЙ отрезок 14 U-1 р1-7 - и Pi - двоичный отрезок Г i iaP- iP- ) Система треугольных кусочно-линых функций Шаудера состоит из кций с максимальным значением 1 пределяется следующим образом: Soo(x) HO(X) 1; S(j(x) . X 2 (x-prr при S(x)Sp. (х) 2 (pTj-x) при х-вКр- при хёВр. Обе системы функций строятся групи, каждая р-ая группа содержит функций. Система кусочно- квадратических функС(х) строится группами с 2 кциями в каждой группе с номер:ЧосМ HO{X) 1-, Чо(х) So(x) Х-, М Чрг.(х) (х х) ; , ; хёСр-, 1,2,,..,N; i 0,1,...,2- -1, I. Первые девять функций системы очно-квадратических функций приены на фиг. 2. В рассматриваемом генераторе ноd кодируется двоичным чисoL, otft,... , djf Аргумент х предвлен двоичным кодом Х,Хп Х, этом в общем случае т7/п. лгоритмы вычисления значений кций Хаара и Шаудера с номером d аргумента х сводятся к следующим ствиям. 1. Для функций Хаара. Осуществляется поиск первой слева ницы в коде dl. Если единица не аружена, то р О, Нд((х) 1, и исления прекращаются. Если в разряде с номером q обнару жена единица, то вычисляется логичес кая функция О ПРИ VA (...Vcin«Xo.. Q 1, то Н(х) х; О, и вычис Если Q О, то ления заканчиваются, Хр кода аргумен анализируется разряд та: Г н-1 при X Н(х) -1 при Хр 1 и на этом вычисления заканчиваются. 2. Для функции Шаудера. Осуществляется поиск первой слева единицы в коде А. Если едуница не об наружена, то р « О, 5д(х) X, и вычисления прекращаются. Если в разряде q обнаружена едини ца, то вычисляется логическая функция Q. Если Q 1 , то Sjji(x) О, и вычисления прекращаются. Если (, ТО анализируется разряд- хр кода аргу мента: при Хр О значение SJJL(X) получается СДВ14ГОМ кода аргумента на р .разрядов влево и считыванием результата в прямом коде, при Хр 1 значение S{JL(X) получается сдвигом кода аргумента на р разрядов влево и считыва нием результата в дополнительном коде. 3. Для системы кусочно-квадратиче ких функций. Значение функции (х) на отрезке может быть получено перемножением прямого и дополнительного кодов аргумента х, сдвинутых влево на р - 1 разрядов: . q«-)( Hl« t%iT|.v Vw xe бр,. Можно предложить следующий алгоритм вычислений. Осуществляется поиск слева единицы в коде d. Если еди ница не обнаружена, то р О, Ч (х) X, и вычисления прекращаются. Если в разряде q обнаружена единица, то вычисляется логическое значение Q. Если Q 1 , то %(,(х) О, Ер г и вычисления прекращаются. Если Q О, то независимо от знамения Хр р-го разряда кода аргумента х он сдвигается на р - 1 разрядов, результат считывается одновременно как в прямом, так и в дополнительном кодах, которые перемножаются как двоичные коды. В результате умножения подучается искомое значение ) , Рассмотренные алгоритмы вычисления значений трех функций с одинаковым значением номера функции d совмещаются. Генератор работает следующим образом . Три значения jjix), ) и /oi,(x) вычисляются за п ,+ 1 тактов работы генератора. При фиксированном значении кольцевого регистра 1 сдвига номера функции cl. вычисляются одновременно все три значения функций. Затем содержимое регистра 1 увеличивается на единицу и вновь повторяется цикл вычисления очередных трех значений функций. После вычисления всех 2 значений функций можно изменить содержимое регистра 2 аргумента и начать вычисления для этого нового значения . В исходном состоянии на регистре 1 установлен код номера функции, на регистре 2 - код аргумента, на регистре и триггерах 6 и 7 установлен нулевой код. На вход 11 начинают поступать тактовые И1 пульсы. Содержимое регистра 2 по первому тактовому импульсу переписывается в регистр 3. С первого выхода блока 10 на тактовый вход регистра 1 поступает серия из п импульсов. С второго выхода блока .вход элемента И 9 поступает серия из п -ь 1 импульсов.. Импульсы, поступающие с выхода блока 10. на тактовый вход регистра 1, вызывают циклический сдвиг его содержимого влево. Пока по цепи циклического переноса циркулируют нули, триггер 6 остается в положении О, а элемент И 9 остается закрытым. На q-oM такте первая единица кода номера функции переписывается из край- . него левого разряда регистра 1 в крайний правый разряд, а триггер 6 переводится в положение 1. Открывается элемент И 9. Теперь управляющие импульсы с второго выхода блока 10, пройдя открытый элемент И 9 поступают на тактовый вход регистра 3 и вызывают сдвиг влево его содержимого Каждый управляющий импульс вызывает теперь поступлекме на входы сумматора 8 по модулю два значений соответствующих разрядов кода номера фун ции и кода аргумента, а на его выходе вычисляется логическое значение Q, запоминаемое триггером 7. При Q 1 (после п-го управляющего импульса) все три функции имеют нулевое значение, что определяется состоянием выхода 14, независимо от состояний выходов 15-17. После прекращения подачи управляющих импульсов на тактовый вход ре гистра 1 на нем находится прежнее зна чение кода номера функции. Управляющие импульсы с (q « 1)-го по п-ый поступившие с второго выхода блока 10 через открытый элемент И 9 на так товый вход регистра 3, вызывают сдви влево его содержимого на р - 1 разрядов . На п-ом такте в множительном блоке 13 производится умножение содержи мого регистра 3 (р« X,jJjO..,0,) на дополнительный код (1-,Хр,. ... .0 содержимого регистра 3, поступающий с выходов блока 12, В этот момент на выходы 17 появляется значение функции ). Последний n+1-ый импульс вызывает еще один сдвиг содержимого регистра и на одноразрядном регистре t сдвига оказывается разряд Хр кода аргумента Если на выходе регистра 4 отсутст вует сигнал, то значение функции Хаара равно +1, а если сигнал имеет ся, то значение функции равно -1. Од новременно выход регистра 4 управляет работой блока 5 преобразования прямого кода в дополнительный: если на выходе регистра 4 сигнал отсутствует, то на выходах 16 блока 5 устанавливается прямой код +1 . содержимое регистра 3, а если на выходе регистра 4 имеется сигнал, то на выходах 16 устанавливается дополнительный код 1 -. содержимого регистра 3. Таким образом, на выходах 15, 16 формируются значения функций Хаара и Шаудера. Предлагаемый генератор имеет более широкие функциональные возможности по сравнению с прототипом, так как он вычисляет наряду с значениями кусочно-постоянных функций Хаара и кусочно-линейных функций Шаудера и значения кусочно-квадратических функций, имеющих значительно лучшие . аппроксимационные свойства. Формула изобретения Цифровой генератор ортогональных функций по авт. св. № 809124, отличающий ся -тем, что, с целью расширения функциональных возможностей, состоящего в возможности генерирования кусочно-квадратических функций, он содержит дополнительный блок преобразования прямого кода в дополнительный и множительный блок, причем выходы разрядов регистра сдвига подключены к первой группе входов множительного блока и через дополнительный блок преобразования прямого кода в дополнительный - к второй группе входов множительного блока, выходы которого являются дополнительными выходами генератора. Источники информации, принятые во внимание при экспертизе 1, Авторское свидетельство СССР № 809124, кл. G 06. F 1/02, 1979 (прототип),
(pue.J



| название | год | авторы | номер документа |
|---|---|---|---|
| Цифровой генератор ортогональныхфуНКций | 1978 |
|
SU809124A1 |
| Цифровой генератор ортогональных функций | 1979 |
|
SU864274A1 |
| Генератор функций Хаара | 1980 |
|
SU947847A2 |
| Генератор функций Шаудера | 1987 |
|
SU1513433A1 |
| Генератор функций хаара | 1978 |
|
SU765796A1 |
| Цифровой генератор функций | 1984 |
|
SU1166091A1 |
| Устройство для отображения графической информации на экране электронно-лучевой трубки | 1984 |
|
SU1243015A1 |
| Генератор функций хаара | 1979 |
|
SU783778A1 |
| Стохастический генератор функций Хаара | 1984 |
|
SU1233131A1 |
| Специализированный процессор | 1977 |
|
SU734705A1 |


Авторы
Даты
1982-05-30—Публикация
1980-05-23—Подача