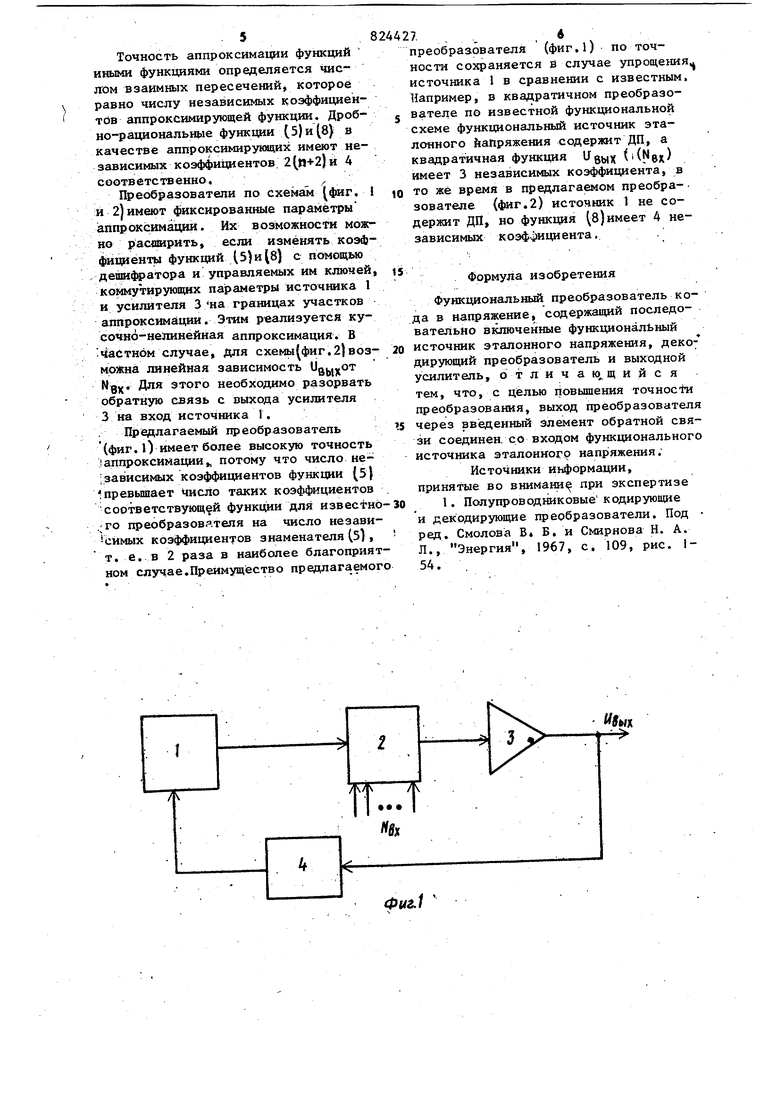
(54) ФУНКЦИОНАЛЬНЫЙ ПРЕОБРАЗОВАТЕЛЬ КОДА В НАПРЯЖЕНИЕ включенный между выхорезистордом усилителя 3 и входом усилителя 5 Устройство работает следующим образсн4. Источник 1 вьфабатывает напряжени и эу для ДП 2, который преобразует входной код N е в напряжение U д,, Последнее поступает на нагрузку через выходной усилитель 3. Для получения нелинейной зависимости от кода NQV выходного напряжения U a,5 напряжение и g-j- должно зависеть от кода .е. источник 1 должен быть функциональным по отношению к коду N вх В схеме (фиг. 1) последнее может достигаться за счет использования, например, второго ДП в источнике 1, В предельном случае кодовый вход источника 1 отсутствует фиг. 2)при этом зависимость напряжения и от кода Ngjjдостигается благодаря обратной связи с выхода преобразователя на вход источника 1. При отсутствии обратной связи через резистор 4 характеристика преобразователя - линейная. При наличии обратной связи ток,, текущий через ре-зистор 4, вычитаясь из тока через резистор ,7 при отрицательной обратной связи, уменьшает напряжение Ug тем больше, чем больще напряжение , поэтому-с ростом кода Ng : напряжения Уд и Цд возрастают все медленнее. Наоборот, при поло штелъной обратной связи ток, теку1ций через резистор 4, складываясь с током через резистор 7, увеличивает напряжение Ug- , поэтому, с ростом кода Ng напряжения и in и возрастают все быстрее. Таким образцом, первая производная напряжения изменяется, что является признакомнелинейности функции . .хК.-Ь --- Bxioin Me4 ain-4 2-W вк...+аклМ ьи из.,1а„,.К ачпм17Я а Для схемы. фиг.2)| ...о1,0 ,p этo ocWвыx выxo) м иэто ос выхо ос вь1Х.. где Kf-r коэффициент отрицательной обратной связи, т. е. коэффициент , lU3,o «oc ebtxo «oc7. .4. Определим вид этой функ1ЩИ для общего случая. AnO и , Обозначим: U первоначальные значения величии эт, UAIJH Ц|И соответственно усйленйе по напряжению и смещение усилителя 3;. S крушзна ДП; , ,(f «вЫкЧU n-U АП д, UAn- BxSU3T.U «o NBXo-S-U3ToW Так как любая функция аппроксимирует-ся степенным полиномом, то для общего случая характеристики источ-/ ника 11) из,т а««ах апм- в; +а«-«вх -- 01 вх «о/деоп ,an-i... OK, ...oii, нные коэффициенты.; В схеме Хфиг«1) обратная связь с ыхода преобразователя на вход источника I вводит зависимость коэфициентов {3 от напряжения U gbix Для аиболее; простой реализации эта завиимость линейная, т. е. aw avo-U Mit,Y4) к °кл - кг аы 1 де а J,. , постоянные коэффициенИз формул )-(4) И14ё&4 Bbix-Ивх т-«Bxo tb -SXy Iftbixo - ex J3 oS-Ky Sbixo S-«4- Bx&a,,,+ П2 -IJBbixi J вч- ln-i) tn- i)i йыкУ ЧN;; M;4ak4 ci.UebixVN8x... ( ci 2-UebixV ex4a 4 a( 02 &Ых)Ъ откуда а„Мвх аоЬ1ивхо-иа-го 1вхо/5: а) ) снижения при отрицательной обт ратной связи} напряжения U под действием напряжения Ug(,|,(. иэ,.хо, Из (5) и (7) после преобразований и (/} пост f схемы фиг.2) UBWxo/S-«y-N8xol 3To) - /S-Ky Точность аппроксимации функций иными функциями определяется чис лом взаимных пересечений, которое равно числу независимых коэффициентов аппроксимирующей функции. Дробно-рациональные функции (5) и (8) в качестве аппроксимирующих имеют независимых коэффи1О1ентов. 2(}1+2) и 4 соответственно,, Преобразователи по схемам |фиг. и 2| имеют фиксированные параметры аппроксимаций. Их возможности можно расширитьt если изменять коэффициенты функций (5) и 8) с помощыо дешифратора и управляемых им ключей коммутирующих параметры источника 1 и усилителя 3на границах участков аппроксимации. Этим реализуется кусочно-нелинейная аппроксимация. В Частном случае, для схемы фиг.2|воз линейная зависимость UnL-vOT м Для этого необходимо разорвать обратную связь с выхода усилителя 3 на вход источника 1. . Предлагаемый преобразователь (фиг. О имеет более высокую точность аппроксимации,, потому что число не; зависимых коэффициентов функции (5) превышает число таких коэффициентов соответствующей функции для H3BectH6 .;го преобразователя на число независймых коэффициентов знаменателя (З), т. е. в 2 раза в наиболее благоприят ном случае.Преимущество предлагаемог 7.,4 преобразователя (фиг.1) по точности сохраняется в случае упрощения источника 1 в сравнении с известным. Например, в квадратичном преобразователе по известной функциональной схеме функциональный источник эталонного йаПряжения содержит ДП, а квадратичная функция UigtHX имеет 3 независимых коэффициента, в то же время в предлагаемом преобразователе (фиг.2) источник 1 не содержит ДП, но функция 8)имеет 4 независимых коэффициента, Формула изобретения Фушищональный преобразователь кода в напряжение, содержащий последовательно включенные функциональный источник эталонного напряжения, деко7 дирующий преобразователь и выходной усилитель, о т л и ч а ю щ и и с я тем, что, с целью повышения точности преобразования, выход преобразователя через введенный элемент обратной связи соединен, со входом функционального источника эталонного напряжения. Источники информации, принятые во внимание при экспертизе 1. Полупроводниковые кодирующие и декодирующие преобразователи. Под ред. Смолова В Б. и Смирнова Н. А. Л., Энергия, 1967, с. 109, рис. 154.

| название | год | авторы | номер документа |
|---|---|---|---|
| Функциональный преобразователь | 1982 |
|
SU1111181A1 |
| Вычислительный узел сеточной модели для решения нелинейных уравнений теплопроводности | 1984 |
|
SU1229783A1 |
| УСТРОЙСТВО для КУСОЧНО-КВАДРАТИЧНОЙ АППРОКСИМАЦИИ ФУНКЦИЙ | 1973 |
|
SU374622A1 |
| Устройство для моделирования транзистора | 1977 |
|
SU708366A1 |
| Диодный функциональный преобразователь | 1986 |
|
SU1365102A1 |
| Устройство для синусно-косинусного цифроаналогового преобразования | 1983 |
|
SU1278897A1 |
| Устройство для воспроизведения функций двух переменных | 1976 |
|
SU637827A1 |
| Функциональный преобразователь | 1985 |
|
SU1267445A2 |
| Функциональный преобразователь | 1977 |
|
SU737963A1 |
| Преобразователь частоты в напряжение | 1983 |
|
SU1190509A2 |



tfffwx
Фui
б
1
tl-T
Фш
Авторы
Даты
1981-04-23—Публикация
1978-06-30—Подача