(54) УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ
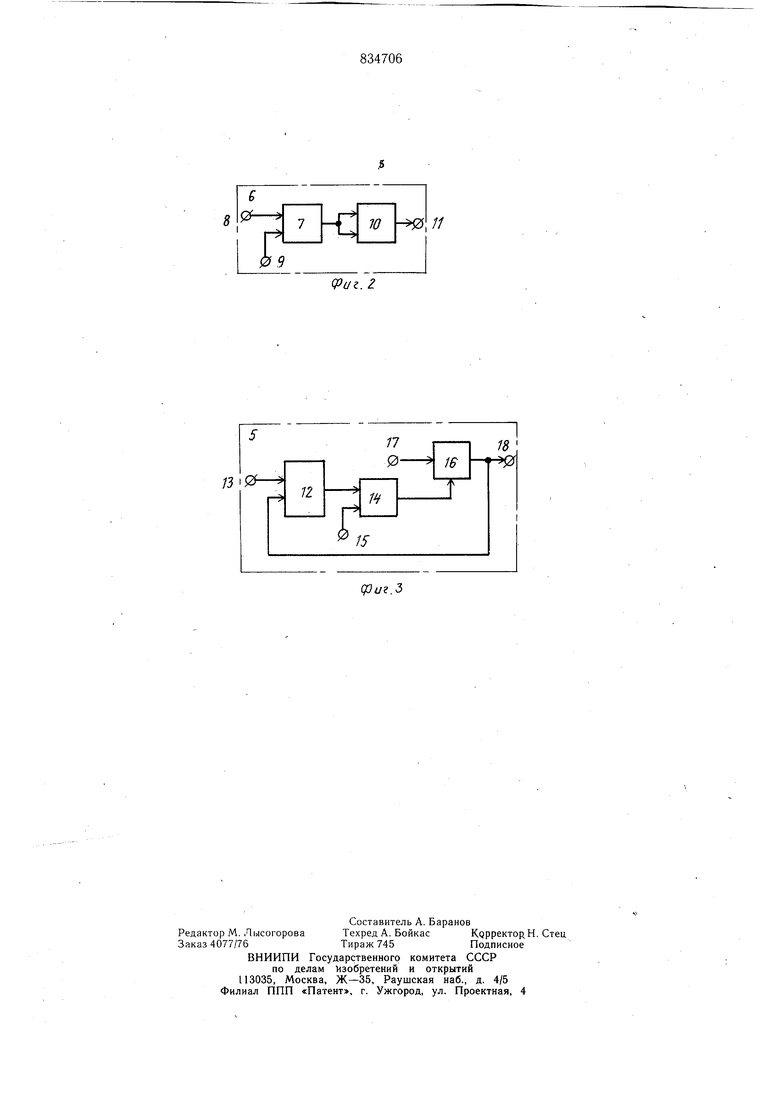
ФУРЬЕ вому входу блока умножения, выход которого подключен к первому входу интегратора, при этом блок выработки критерия содержит сумматор и блок умножения, входы которого соединены с выходом сумматора, первый вход которого является входом устройства, выход сумматора соединен со вторым входом сумматора блока выработки критерия, выход блока умножения которого подключен ко второму входу дифференцирующего блока i-ro (i , 2N + 1) экстремального регулятора, выход интегратора которого соединен со вторым входом i-ro блока умножения, а выход интегратора (2N + 1)-го экстремального регулятора подключен к(2М4-1)-му входу сумматора, причем вторые входы дифференцирующих блоков и интегрирующих блоков всех экстремальных регуляторов являются соответственно первыми и вторыми группами входов устройства. На . 1 представлена схема устройства для вычисления коэффициентов Фурье; на фиг. 2 - схема блока выработки критерия; на фиг. 3 - схема экстремального регулятора. Устройство содержит источник 1 анализируемой функции, сумматор 2, генератор 3 ортогональных функций, блоки 4 умножения, экстремальные регуляторы 5, блок 6 выработки критерия, сумматор 7, 1-й 8 и 2-й 9 входы сумматора, блок 10 умножения, выход 11 блока 6, дифференцирующий блок 12, вход 13 регулятора 5, блок 14 умножения 2-й 15 вход блока 14 умножения, интегратор 16, вход 17 независимой переменной интегратора 16, выход 18 регулятора 5. Функционирование устройства осуществляется следующим образом. Пусть в i-M такте на вход 17 экстремальных регуляторов подано приращение At, которое, будичи умноженным в интеграторах 16 на величину-i- ()- или -- (||)f-) где Ое-косинусные коэффициенты Фурье (1 0, 1., 2,..., N); йк -синусные коэффициенты Фурье (К 1, 2,...,N), дает на выходах соответствующих экстремальных регу«Я дар/ -(lS-).,t ляторов приращения XAt и Д8 к,- { If-) ( Дt соответстобк ,венно. Приращения (1 1, 2,...,N) и ДКк1(К 1, 2,...,N), будучи умноженными в блоке 4 величины A(coslwt), и A(sinKu)t)i. соответственно, дают на их выходах приращения A()t)/ и A(8,inK(ot), соответственно, которые, будучи сложенными в сумматоре 2 с приращением , дают на его выходе приращение Д{( А ас + + Ejfo:cosj0t + ejsinj at)jj- Это приращение поступает на вход 8 блока 6 выработки критерия, где, будучи сложенным в сумматоре 7 с приращением Afj, поступившим на инверсный вход 9 с выхода блока 1, дает на его выходе приращение A(f,- f); , которое, будучи умноженным в блоке 10 на себя, дает на его выходе 11 приращение целевой функции F uFf A(f,- f)j2 , поступающее на входы 13 блоков 12 экстремальных регуляторов 5, на вторые входы которых поступает соответствующее приращение &ац или На выходе блока 12 появится соответствующее приращения Д() или Д(|-)«, которые, .будучи умноженными в блоке 14 на величину -, на их выходах приращение -ф-Д(), (-$-); , которые вызывают накопление в соответствующих интеграторах - F ()i или-(.. 16 величин хранимых здесь до наступления (i + 1)-го такта, вызываемого новой подачей приращения At на выходы 17. Процесс вычисления коэффициентов Фурье заверщается при достижении целевой функцией минимума, то есть когда F; Ftni (f г - f)(it. Оо + + S(ajcosj (i)t + g,-sinj u)t) - f ftnm Отсю - ff да aoi+ ,( cosj iot + 6ji sinjfijt) f;-f fFmin. sin(f - f) , где aji,Bji- - соответственно, j-e косинусные и синусные коэффициенты Фурье функции f в м такте, «Гв/ - нулевой коэффициент Фурье, f; - значение функции f в момент времени i ti. Закон функционирования устройства задается следующей системой дифференциальных уравнений: Т WT - т « +1(«; °J + i -f(t)2 0, О, 1, 2, df-- Т-|/ + - а, + r(Qjcosja)t + ftjsinjo b f(t)2 О, К 1, 2,..., N; где Oj и 8j - косинусный и синусный j-e коэффициенты Фурье; Ов-нулевой коэффициент Фурье; f(t)-разлагаемая в ряд Фурье функция. Таким образом, процесс получения коэффициентов Of и 8 заключается в постоянном обеспечении наименьщего значения выражения F jOp + (ajcosjujt + Sjsinjtttjf(t)p, a значит и интеграла S Х- РсЙ являющегося средним квадратичным уклонением от функции f(t). Среди всех тригонометрических многочленов порядка N наименьшее среднее квадратичное уклонение 8 от функции f(t) имеет тот многочлен, коэффициенты которого суть коэффициенты Фурье функции f(t). Во всех известных устройствах для вычисления коэффициентов Фурье обеспечение наименьшего значения S является следствием вычисления коэффиентов Фурье, в предлагаемом устройстве коэффициенты Фурье получаются как следствие процесса обеспечения наименьшего значения 5, т.е. при таком новом подходе на первый план выступает обеспечение наибольшей точности представления функции данным набором коэффициентов. Обеспечение возможности вычисления непрерывно во времени коэффициентов Фурье делает устройство более универсальным и обладающим более широкой областью применения по сравнению с прототипом. Формула изобретения Устройство для вычисления коэффициентов Фурье, содержащее сумматор, генератор ортогональных функций, i-ый выход (i 1, 2N) которого соединен с первым входом i-ro блока умножения, выход которого соединен с первым входом сумматора, отлиtчающееся тем, что, с целью расширения функциональных возможностей увеличения точности вычислений за счет вырабатывания непрерывно во времени коэффициентов разложения функции, в него введены блок выработки критерия и 2N 1 экстремальных регуляторов, каждый из которых содержит дифференцирующий блок, блок умножения и интегратор, выход которого соединен с первым входом дифференцирующего блока, выход которого подключен к первому входу блока умножения, выход которого подключен к первому входу интегратора, при этом блок выработки критерия содержит сумматор и блок умножения, входы которого соединены с выходом сумматора, первый вход которого является входом устройства, выход сумматора соединен со вторым входом сумматора блока выработки критерия, выход блока умножения которого подключен ко второму входу диффренцирующего блока i-ro (i -f 1, 2N + 1) экстремального регулятора, выход интегратора которого соединен со вторым входом i-ro блока умножения, а выходинтегратора (2N + 1)-го экстремального регулятора подключен к 2N Ч- 1-му входу сумматора, причем вторые входы дифференцирующих блоков и интегрирующих блоков всех экстремальных регуляторов являются соответственно первыми и вторыми группами входов устройства. Источники информации, принятые во внимание при экспертизе 1.Авторское свидетельство СССР № 560232, кл. G 06 F 15/34, 1975. 2.Авторское свидетельство СССР № 446J373, кл. G 06 G 7/19, 1972.


| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для вычисления коэффициентовфуРьЕ | 1979 |
|
SU824218A1 |
| Дифференцирующее устройство | 1979 |
|
SU922739A1 |
| Аналоговое вычислительное устройство | 1987 |
|
SU1506456A1 |
| Аналоговое устройство для определения частной производной | 1982 |
|
SU1053065A1 |
| Стохастический фильтр | 1989 |
|
SU1675905A1 |
| Цифровой интегратор | 1980 |
|
SU879586A1 |
| Устройство для определения спектральных коэффициентов разложения случайного процесса по функциям Хаара | 1980 |
|
SU935814A1 |
| Устройство для вычисления коэффициентов фурье-хаара | 1975 |
|
SU579623A1 |
| Устройство для решения систем дифференциальных уравнений | 1987 |
|
SU1476502A1 |
| Интегроарифметическое устройство | 1990 |
|
SU1784975A1 |


дЗиг.2
Авторы
Даты
1981-05-30—Публикация
1979-06-04—Подача