Изобретение относится к автоматике и вычислительной технике и может : быть использовано для обработки двумерных сигналов, .изображений, для анализа спектров случайных полей/в аппаратуре сжатия информации при передаче данных и т.д.
Известен анализатор спектра по функциям хаара, содержащий аналогоцифровой преобразователь, интегратор, -регистры сдвига, сумматоры и ключи 1.
Наиболее близким по технической сущности к предлагаемому является устройство для выполнения дискретного преобразования, содержащее N групп блоков, каждая из которых состоит из трех сумматоров-вычислителей и трех регистров сдвига 2.
Недостатком известных устройств являются ограниченные функциональные возможности, поскольку они предназначены для вычисления коэффициентов только одновременного преобразования Хагра (Уолша) и .не могут производить двумерное преобразование дискретных сигналов.
Цель изобретения - расширение функциональных возможностей устройства.
состоящего в возможности выполнения двумерного преобразования Хаара.
Поставленная цель достигается тем, что в устройстве для выполнения дискретного преобразования Хаара, соN
держащем N групп блоков (4
число
коэффициентов двумерного преобразования) ,каждая из которых состоит из трех сумматоров-вычитателей и трех
10 регистров сдвига, причем первый и второй входы i-ro сумматора-вычитателя п-й группы (,2,3; п 1-N) соединены соответственно со входом и выходом i-o регистра сдвига п-й группы, вход первого регистра сдвига первой группы является входом Устройства, выходы суммы и разности пер: вого сумматора-вьачитателя каждой группы подключены ко входам второго
20 и третьегорегистров сдвига той же группы, выход суммы второго сумматора-вычитателя л-и группы, кроме N-й группы, подключен ко входу первого регистра сдвигап+1-й группы,
25 выходы разности первых и вторых сумматоров-вычитателей, выходы суммы и разности третьих сумматоров-вычитателей всех групп, а также выход суммы второго сумматора-вычитателя N-ой
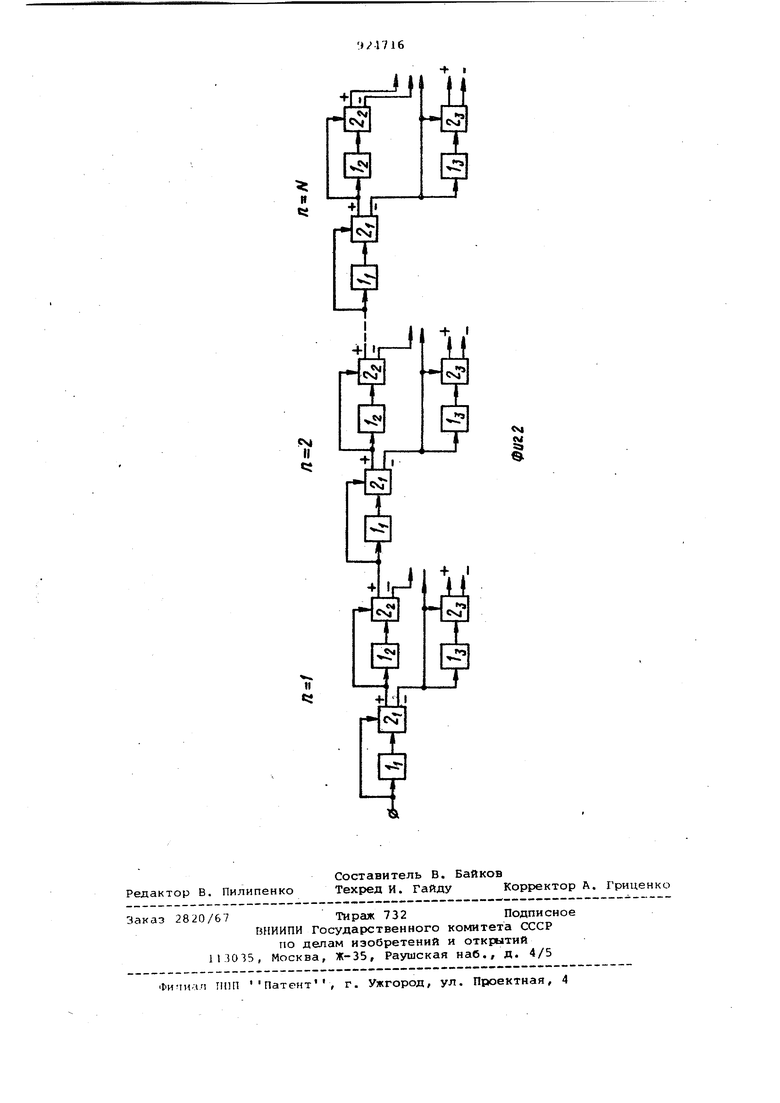
30 группы являются выходами устройства. Ил фиг. 1 показами первые шестнадцать функций Хаара двух переменных; на фиг. 2 - функциональная схе ма устройства для выполнения дискре ного преобразования Хаара. В предлагаемом устройстве осуществляется последовательная дискретная обработка 4 значений входного сигнала с целью получения 4 коэффициентов дискретного разложени в базисе функций Хаара от двух пере менных или 2 коэффициентов ( N) дискретного разложения в базисе фун ций Хаара одной переменной. При выполнении одномерного дискретного преобразования Хаара на вхо устройства должны поступать последо вательно 2 значений входного сигнала, а при выполнении двумерного преобразования, на вход устройства долж поступать последовательность из 4 значений входного двумерного сигнала упорядоченные определенным образом. Например, для N 2 и М 4 шестнадцать отсчетов двумерного входного сигнала y(,qj) должны поступа на вход в следующем порядке: у , у Yai У11 У-13 14 У1Ъ УЭУЬ1 У 4-1 У 41 У-ЬЪ УЪА- У4Ь У 44 а шестнадцать отсчетов одномерного входного сигнала (ti-) должны поступать на вход в естественном порядке х, X г2,, х, х, Х5-, х, х-,, Xg, Xg, , Х, X. fl , , , Так как две приведенные последо вательности имеют одинаковое число элементов, то можно говорить о соответствии некоторого элемента первой последовательности элементу второй п следовательности. Например, элемент у, соответствует элементу х-, так как оба они имеют одинаковый порядковый номер. Запишем с точностью до постоянного множителя явные выражения для 16-ти коэффициентов дискретного одно мерного преобразования Хаара входного сигнала х :; х (t.;) : vP/i АО.jb Q ру.-С г-9 -л (Я -.л «5 а4 ,)- (xj+ Х4.) a5 (xj+Xjj)-( Xg) a(Xg+X,g)-(Xi,+ X.,,) a-, ()-(x.jf x ag x/j a.,(5 xgа х/ц XiQ a2 X4 а 1 д X ,- X14 ХЕ- X, х,- Х( 15 15 1( Дискретное оптогональное двумерное преобразование Хаара для сигнал - y(t,qj) определим с точностью постоянного множителя следующим азом: Ч-.5С.,и.(,д, Ч -последовательностьиз 4 коэффициентов L двумерного дискретного преобразования Хаара; ),:o -система базисных ненормированных ортогональных трехзначных функций Хаар двух переменных. ример, для последовательности из и значений у-л входного сигнала двумерное, дискретное преобразоие Хаара определяется следующим азом: c, pp,j 11.1 jii с ( (y +y ii+yti +y + (у,,+У 4+Уаз У24) 1+Узг1.+У4,+У4а- У1 г+ У УЛ tL ((,fi+y, (Уз.+Уза+У41+У4а) г+ У.4 - Уаз + ) + (Узз+Уг4+У4ь- У44 5 ((,+у,а..) + ( ) г+У14- Угг У14 Узл+Уг +У4 М с 4 (у,, + yia-%+ yrii с 5 (У + )-( с 6 (У,, + (y,fi+ УЧ,} т (у,з+ Уа4 eg {У-,-ь- Уи)-(У-14+ У1А 9 У,) ( c-((7(yj,+ Уза)-(У41+ Уда) С11(Уз,- У4. )-(Уз7- Уд) с,а (Уз,- У4а)-(Уза+ Уд.) ( У)-(У4я+ y.J 43 44 Угг Уи (yj.j+ У44)-(У41 Уз4)Заменяя в выражениях (4) элементы с двухпозиционным индексом соотствующими элементами х , с однопоионным индексом 1- У-ц/ Х у,,, Х, у, Хд уаг,..., х. Уд,, учим ve 11 / 8 1Ь С„:: ЕХ.+ СХ. Ь1 i-.з / -иг /4 б /« г Vtox i:ix, - 1 i:( / ;г5 i--9
Сд (х f XnJ - {х j + х)
Cj-- (Х + X j)- (Х ( + Хд) С (X «- Х)- (X Х) С-, (Х J + X j)- (Х , Н- Хд)
са (X 5 + XT)-{X 6 + xg)
(5)
Cg (Xj.+ Xg)-(X(,+ X)
c(5 (X q + )- (x ,,,+ ) CM (« 9 + x)-(x 0+ x)
Ci (Xg + X)-(X,(,+ X,)
Cir ь+ и) ь (x-,,,+ Xi5)-( x)
(Xii,+ )-( ) Сравнивая (2) и (5), убеждаемся, что коэффициенты с,-., с, 04, с-,, с д и с двумерного преобразования соответствуют коэффициентам ад, а, , а, и а-, одномерного преобразования Хаара, Таким образом, поступление на вход предлагаемого устройства отсчетов у4; в опр.еДеленном порядке (1) позволяет унифицировать процедуры вычисления коэффициентов Хаара при одномерном и двумерном преобразовании.
Устройство работает следующим образом.
IlifcTb на вход устройства поступают 16 значений одномерного входного сигнала х {N 2, М 4) . В регистре сдвига1 первой группы (п 1) сигнал х, поступивший в первом такте задерживается на один такт и на сумматор-вычитатель 2 этой группы в втором такте поступают значения х, и XQ. На выходах суммы и разности сумматора-вычитателя во втором такте формируются значения х + XQ и х - xrj второе из которых является коэффициентом одномерного преобразования Хаара ag.
В третьем такте на выходах сумматора-вычитателя 2 сформируются значения и x.,a в четвертом .такте - значения Х5+Х4.и Xi,-x.. Значение Xj- Хд является коэффициентом ад одномерного преобразования Хаара, этот коэффициент может быть считан в конце четвертого такта.
Аналогично работают регистры сдвига IQ , 12, и сумматоры-вычитатели 24, 2ij первой группы, с той лишь разницей, что регистры сдвига 1 rj и Ij задерживают сигнал на два такта. В результате на четвертом такте работы сформируются три коэффициента, соответствующие двумерному преобразованию Хаара, один из которых является коэффициентом одномерного преобразования Хаара:
(х -ьх ) - (х j+x) с выхода раности блока 2(;
С5 () + () с выхода суммы блока 2 3;
c«, () - (х,|-Хд) с выхода разности блока 2.
, Значение х,+ Xj+ х с выхода суммы сумматора-в(лчитателя 2 ( первой группы (п 1) поступает на вход регистра сдвига 1 второй группы (). Работа во всех блоков первой группы на последующих, вплоть до 16-го такта не отличается от рассмотренной.
На 6,8,10,12,14 и 16-м тактах работЕя на выходе разности сумматора вы- читателя 2 первой группы формируются соответственно коэффициенты , 15 а , , 11, 4 а одномерного преобразования Хаара.
На 8-ом такте блокаМи первой группы формируются три коэффициента, соответствующие двумерному преобразованию Хаара, и один коэффициент одномерного преобразования:
aj с на выходе разности блока
Сд на выходе суммы блока 2д; сд на выходе разности блока 2j; на 12-м такте:
на выходе разности бло Ь ка
с на выходе суммы блока 2L; с на выходе разности блока 23; на 16-м такте:
а -, на выходе разности блока 2,
на выходе суммы
ка 2
С;,;- на выходе разности бло0ка 2з.
Величина згщержки в регистрах последующих групп устанавливается следующим образом: 4 тактов в регистре 1/, п-й группы; тактов - в 5 регистрах 1, 1-j г-и группы.
Регистр сдвига 1 -, второй группы Зсщерживает входной дискретный сигнал на 4 такта, а регистры сдвига l-j,- на 8 тактов. Поэтому на вып ходе разности сумматора-вычитателя 2 второй группы на 8 и 16-ом тактах формируются коэффициенты а, aj одномерного преобразования Хаара. На 16-ом такте блоками второй группы форя«1ируются следующие коэффициенты: а с 1 на выходе разности блока 2i;
Сп на выходе суммы блока 2j; с на выходе разности блока 2 j; 0 а о CQ на выходе суммы блока 2fj.
На этом работа устройства заканчивается.
Работа устройства при N 7 2 принципиально ничем не отличается от только что рассмотренной. В общем случав
значения всех 4 коэффициентов двумерйого или одномерного преобразования Хаара вычисляются за тактов работы устройства.
Таким образом предлагаемое устройство способно вьшолнять дискретное преобразование Хаара либо в одномерной, либо в двумерной области.
Формула изобретения
Устройство для выполнения дискретного преобразования Хаара, содержащее N групп блоков ( - число коэффициентов двумерного преобразования), каждая из которых состоит из трех сумматоров-вычитателей и трех регистров сдвига, причем первый и второй 1ВХОДЫ 1-го сумматора-вычитателя п-й группы (.,2,3,п 1 - N) соединены соответственно со входом и выходом 1-О регистра сдвига п-й группы, вход первого регистра сдвига первой группы является входом устройства, о т лишающееся тем, что, с целью расширения функциональных возможностей устройства, состоящего в возможности выполнения двумерного преобразования Хаара, в нем выходы суммы и разности первого сумматора-выг читателя каждой группы подключены к входам второго и третьего регистров сдвига той же группы, выход суммы второго сумматора-вьгчитателя t -и группы,кроме N-й группы подключен к входу
Q первого регистра сдвига п +1-й групп л, выходы разности первых и вторщх сумматоров-вычитателей, выходы суммы и разности третьих сумматоров-вычитателей всех групп, а также выход суммы второго сумматора-вычитателй
К-й группы являются выходами устройства.
Источники информации, принятые во внимание при экспертизе
1.Авторское свидетельство СССР
№ 484523, кл. G Об F 15/34/20.02.74.
2.Авторское свидетельство СССР 620974, КЛ.С 06 F 5/00,27.05.70 (прототип).



| название | год | авторы | номер документа |
|---|---|---|---|
| Параллельный процессор Хаара | 1989 |
|
SU1667103A1 |
| Поточно-параллельный процессор Хаара | 1989 |
|
SU1756901A1 |
| Устройство ортогонального преобразования | 1988 |
|
SU1594563A1 |
| Устройство ортогонального преобразования по уолшу | 1976 |
|
SU620974A1 |
| Устройство для преобразования булевых функций | 1988 |
|
SU1532946A1 |
| Устройство для выполнения обратного преобразования Хаара | 1983 |
|
SU1104528A1 |
| Устройство для преобразования по функциям Хаара | 1986 |
|
SU1327119A1 |
| Устройство для ортогонального преобразования цифровых сигналов по Хаару | 1988 |
|
SU1594561A1 |
| Многоканальное устройство для ввода аналоговых данных | 1986 |
|
SU1335972A1 |
| Устройство для быстрого преобразования Уолша-Адамара | 1988 |
|
SU1536398A1 |


о xi-0 f
Id
я
r«J
.
t.
П
е«
еч Н
«:;
м
Ir
f .1
Авторы
Даты
1982-04-30—Публикация
1980-08-25—Подача