(54) АНАЛОГОВЫЙ ИНТЕГРИРУЮЩИЙ ВЫЧИСЛИТЕЛЬ
1
Изобретение относится к вычислительной технике и системам автоматики и может быть использовано в преобразователях интегральных параметров сигнала и спектроанализаторах.
Известен фильтр нижних частот, содержащий сигнальный и итоговый интеграторы и ключи, который реализует в зависимости от выбора программы работы ключей фильтрацию нижних частот с кусочно-номинальными окнами, или весовыми функциями Дирихле (прямоугольное окно), Бартлетта (треугольное окно), параболической и другими 1 .
Известен также аналоговый интегри.рующий вычислитель, содержащий интегрирующие усилители и ключи, реализук щий весовую функцию Блэкмана 2 .
Недостатки известных устройств заключаются в том, что они реализуют неоптимальные весовые функции, проигрывающие оптимальному окну Папулиса.
. Наиболее близким к предлагаемому гюляется вычислитель, содержащий по-
следовательно соединенные сигнальные интегрирующие усилители, подключенные через первый ключ к первому входу выч. ходкого интегрирующего усилителя, второй вход которого через первый масшта&ный блок и второй ключ соединен со входом вычислителя, подключенным через второй масштабный блок к первому входу первого сигнального интегрирук щего усилителя, а также инвертирукнций
10 усилитель, вход которого через третий масштабный блок подключен к выходу второго сигнального интегрирующего усилителя, а выход х:вязан со вторым входом первого интегрирующего усилителя ГЗ .
15 Недостатком этого вычислителя является невысокая точность работы в услови5ис действия сосредоточенных по спектру низкочастотный помех.
20
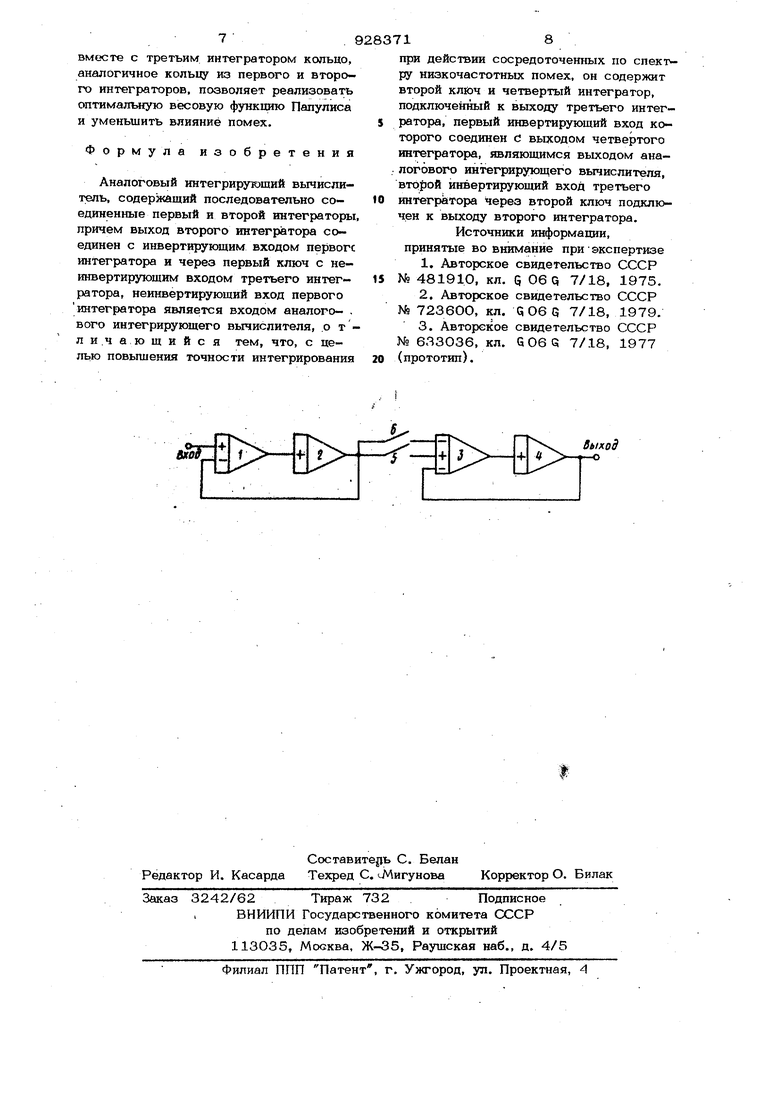
Цель изобретения - повышение точности интегрирования при действии сосредоточенных по спектру низкочастотных помех., Указанная цель достигается тем, что аналоговый интегрирующий вычислитель, содержащий последовательно соединенны первый и второй интеграторы и первый ключ, причем выход второго интегратора соединен с инвертирующим входом первого интегратора и через первый клю с неинвертирующим входом третьего интегратора, неинвертируюший вход первого интегратора 5тляется входом аналогового интегрирующего вычислителя, содержит, второй ключ и четвертый интегратор, подключенный к выходу третье го интегратора, первый инвертирующий вход которого, соединен с выходом четвертого интегратора, явл5пощимся выходом аналогового интегрирующего вычислителя, второй инвертирующий вход третьего интегратора через второй ключ подключен к выходу второго интегратора На чертеже представлена функциональ ная схема аналогового интегрирующего вычислителя. Вычислитель содержит первый Интегратор 1, второй интегратор 2, третий интегратор 3, четвертый интегратор 4, первый ключ 5, второй ключ 6. Интеграторы 1 и 2 соединены последовательно, выход интегратора 2 соединен с входом интегратора 1 и через ключ 5 - с первым входом интегратора 3, а через ключ 6 - с вторым входом интегратора 3. Выход интегратора 3 соединен с входом интегратора 4, выход которого связан с третьем входом интегратора 3 и является выходом устройства. Предлагаемый аналоговый интегрирую щий вычислитель реализует окно Папулис Wptt)r. WJi)|- s-inctt-aico5cit nPHOitiт оД «, л . с|г . , ,- .,1 11 )sitial4Ji-at)cosqt npM i., инйче о где q - коэффициент передачи любого интегратора по любому входу. Работу вычислителя в двух интервалах рассмотрим раздельно. . В течение первого интервала |о, замкнут ключ 6, ключ 5 разомкнут. На втором интервале замкнут ключ 5, ключ 6 разомкнут. При нулевых начальных условиях выражение передаточной .функции двух последовательно включенных интеграторов 1 и 2 или 3 и 4 с обратной связью (кольца), как для линейной системы, имеет вид HCs) где д - оператор одностороннего преобразования Лапласа. 1. Интервал О; |-. Передаточная функция определяется как произведение передаточных функций двух колец из интеграторов 1-2 и 3-4 при замкнутом ключе 6 ,(s)(.i) Импульсная переходная функция b(t))};-|-(Sindt-oitc05clt; Определим выходную величину для четвертого по схеме (фиг. 1) интегратора на конце интервала t 2(t).j(t-)()a-sr ii (()co5au.aCL)di; о Дополнительно найдем выходную величину для первого интегратора на конце интервала. Она будет необходима для учета ненулевых начальных условий во втором интервале. Выражение для передаточной функции участка кольца до выхода перВого интегратора через передаточные функции кольца и второго интегратора 0 t3S )rH(S)/H(.S) Соответствующая ИПФ равна (fc):qcosott Теперь окончательно получим dCoec(-t-t)(C) c«ooedC-(Cldt о .о 2. Интервал -о- - Проведем исследование методом суперпозиции. Часть 1 результата создаётся ненулевыми начальными условиями без учета входного сигнала, часть 2 создается сигналом при нулевых начальных условиях. Ч а ь 1. Учтем, что длина интервала- -1- равна половине периода свободных колебаний каждого из колец. Начальное условие 2 J/d на четвертом интеграторе вызывает косинусоидальный процесс на выходе и через полпериода
произойдет смена знака при том же мо- дуле, т. е.
I d
OJi --1Л - Itsincir4(jr.ait)cosair t)dT(г) а о
Начальное условие на третьем интеграторе вызывает синусоидальный процесс на выходе и его вклад, измеренный по истечении полупериода, будет равен нулю.
Ненулевое начальное условие А на втором интеграторе приводит к появлению косинусоидального процесса на входе второго кольца. Импульсная переходная функция (ИПФ)ЭТОГО кольца является синусоидальной функцией времени с тем же периодом. Свертка этих двух функций на интервале, равном половине периода; дает нулевой результат:
ча а
ал
d
о15лл (I-irJA eos Sin aqtdi: o
l о
ЗГ
5
r
Начальное условие Z на выходе первого интегратора вызывает на входе второго кольца синусоидальный процесс
вида
Vj/ -Sindt
Свертывание его с синусоидальной ИПФ кольца дает вклад
1Л
q.
jT/aS -a-sin(t-)dc-|v-,
T.
Здесь первый сомножитель под знаком интеграла представляет переходной процесс от ненулевого начального условия первого интегратора, а второй сомножитель - -это ИПФ второго кольца.
Используя для Vl/d , запишем развернутое соотношение -
V/d-S -)
о.
Итог части 1 запишется как сумма (2 и (3)
л d
.Tt ((r-qrcoSciC)(C)dr
ri J
Эта формула представляет собой результат обработки сигнала на первом интервале с весом
Гс1
-( cosa-fc) ПРИ o..
«i(t).
W
иначе О
В формировании данного результата принимали участие свободные колебания во втором интервале.
Часть 2. После того, как учтены все составляющие, возникшие в результате действия сигнала (t) в первом интервале, определим результат обработч ки сигнала a(t) во втором интервалеГ Поскольку обработка начинается в момент t , из аргумента ИПФ следует вычесть g
j 5 a t-C-)-d(i-c4Hax
-I
()) 5 (Ji-qC)cx)St
3i d
X :(т)ат
30
Результат получен такой, как если бы сигнал обрабатывался с весом
c(i+(ji-cit)co5dt ПРИ , 4l.-t).(5)
ииошео
Сопоставление (4) и (5) с (1) позволяет заключить, что структура реализует ВФ Папулиса с точностью до постоянного множителя.
Достоинства окна Папулиса известны: его спектр имеет минимальный центральный второй момент. По сравнению с окном Хэмминга, реализуемом в известном вычислителе, окно Папулиса подавляет помехи в ближней части зоны непрозрачности на 3 дБ сильнее, а скорость спада боковых лепестков составляет 24 дБ/ /октава против 6 дБ/октава.
Эффект от применения предлагаемого вычислителя заключается в увеличении точности при работе в условиях помех. Подобные помехи, в частности, всегда имеются в виде переменной составляющей на выходе детекторов. Применение четвертого интегратора, образующего вместе с третьим интегратором кольцо, анапогичное кольцу из первого и второго интеграторов, позволяет реализовать оптимальную весовую функцию Папулиса и уменьшить влияние помех. Формула изобретения Аналоговый интегрирующий вьиислитель, содержащий последовательно соединенные первый и второй интеграторы причем выход второго интегр1атора соединен с инвертирующим входом первого интегратора и через первый ключ с неинвертирующим входом третьего интегратора, неинвертирующий вход первого интегратора является входом аналого- . вого интегрирующего вычислителя, о т ли чающийся тем, что, с целью повьпиения точности интегрирования 18 при действии сосредоточенных по спекч ру низкочастотных помех, он содержит второй клич и четвертый интегратор, подключенный к выходу третьего интегратора, первый инвертирующий вход которого соединен d выходом четвертого интегратора, являющимся выходом аналогового интегрирующего вычислителя, второй инвертирующий вход третьего интегратора через второй ключ подключен к выходу второго интегратора. Источники информации, принятые во внимание при экспертизе 1.Авторское свидетельство СССР № 481910, кл. 5 06Q 7/18, 1975. 2.Авторское свидетельство СССР NO 7236ОО, кл. QO6Q 7/18, 1979. 3.Авторское свидетельство СССР № 633036, кл. G06G 7/18, 1977 (прототип).


| название | год | авторы | номер документа |
|---|---|---|---|
| Аналоговый интегрирующий вычислитель | 1978 |
|
SU723600A1 |
| Аналоговый интегрирующий вычислитель | 1977 |
|
SU633036A1 |
| УСТРОЙСТВО И СПОСОБ ИЗМЕРЕНИЯ ПЕРЕМЕННОЙ ВЕЛИЧИНЫ | 2010 |
|
RU2437064C1 |
| Устройство для измерения температуры | 1984 |
|
SU1185119A1 |
| Способ определения входного сопротивления усилителя заряда и устройство для его осуществления | 1984 |
|
SU1205060A1 |
| Электрометрический преобразователь заряда | 1986 |
|
SU1420537A1 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ УСКОРЕНИЙ | 1999 |
|
RU2163380C1 |
| Экстраполятор | 1980 |
|
SU934504A1 |
| Интегратор | 1988 |
|
SU1728871A1 |
| Интегратор | 1980 |
|
SU922786A1 |



Авторы
Даты
1982-05-15—Публикация
1980-08-25—Подача