Известны устройства для построения различных кривых второго порядка с заданными параметрами. Недостатком их является то, что они имеют сложную конфигурацию, а усилия трения в мертвых положениях этих устройств достигают значительных величин, что отражается на точности их работы.
Описываемое устройство основано на принципе проекционного преобразования окрул ности в кривую второго порядка (коническое сечение). Устройство имеет простую конструкцию, в нем нет мертвых положений, в связи с чем на чертящее приспособление не оказывают заметного влияния силы трения.
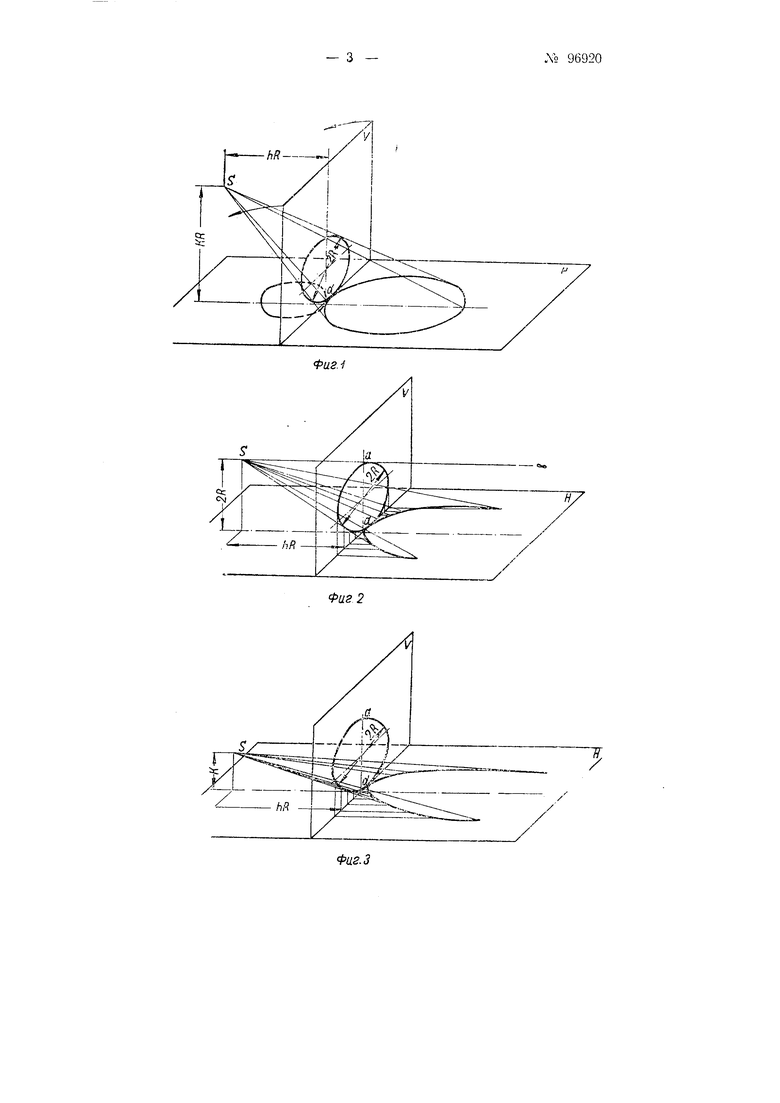
На фиг. 1 показана схема проекционного преобразования окружности в эллипс; на фиг. 2-преобразование окружности в параболу; на фиг. 3-в гиперболу; на фиг- 4-схема совмещения вертикальной плоскости (фиг. 1) с горизонтальной; на фиг. 5-схема устройства.
Построение кривых второго порядка основано на следующем: пусть даны две взаимно-перпендикулярные плоскости Н и V (фиг. 1) и полюс S. На плоскости V изображена окружность, касающаяся оси пересечения плоскостей в точке а. Для того, чтобы спроектировать окружность с плоскости V на плоскость Н, из полюса нужно провести лучи через точки окружности до встречи их с плоскостью Н. Если соединить спроектированные точки, то на плоскости Н получится эллипс. Если теперь перемещать полюс S вверх или отдалять его от плоскости V, то будет соответственно меняться форма эллипса на плоскости Н. Окружность на плоскости V имеет диаметр равный 2R. Полюс S отстоит от плоскости V на расстоянии hR, а от плоскости Н на расстоянии KR. При перемещении полюса S вверх наступит момент, когда на плоскости Н больщая и малая оси эллипса будут равны, т. е. будет проектироваться окружность. При дaльнeйщe пере.мещении полюса вверх, у эллипса бывщая большая ось станет меньше бывщей малой оси.
№ 96920- 2 -
При перемещении полюса S вниз (фиг- 2) большая ось эллипса будет неограниченно расти. Когда полюс S достигнет расстояния от плоскости Н, равного диаметру окружности 2R, т. е- когда К 2, тогда точка а, лежащая на окружности в плоскости V, не спроектируется на плоскость Н; проекция этой точки уйдет в бесконечность ( схэ). Как бы ни менялось положение полюса относительно плоскости V (расстояние hR), во всех случаях на плоскости Н при KR 2R будет проектироваться парабола. При дальнейн1ем перемещении полюса S вниз, т. е. при , иа плоскость Н споектируется гипербола. В данном случае уже проекции двух точек окружности, лежащих на уровне полюса, уходят в бесконечность (фиг. 3). Проек.тирование из полюса S окружности, лежащей в плоскости V, на плоскость Н и является проекционным преобразованием.
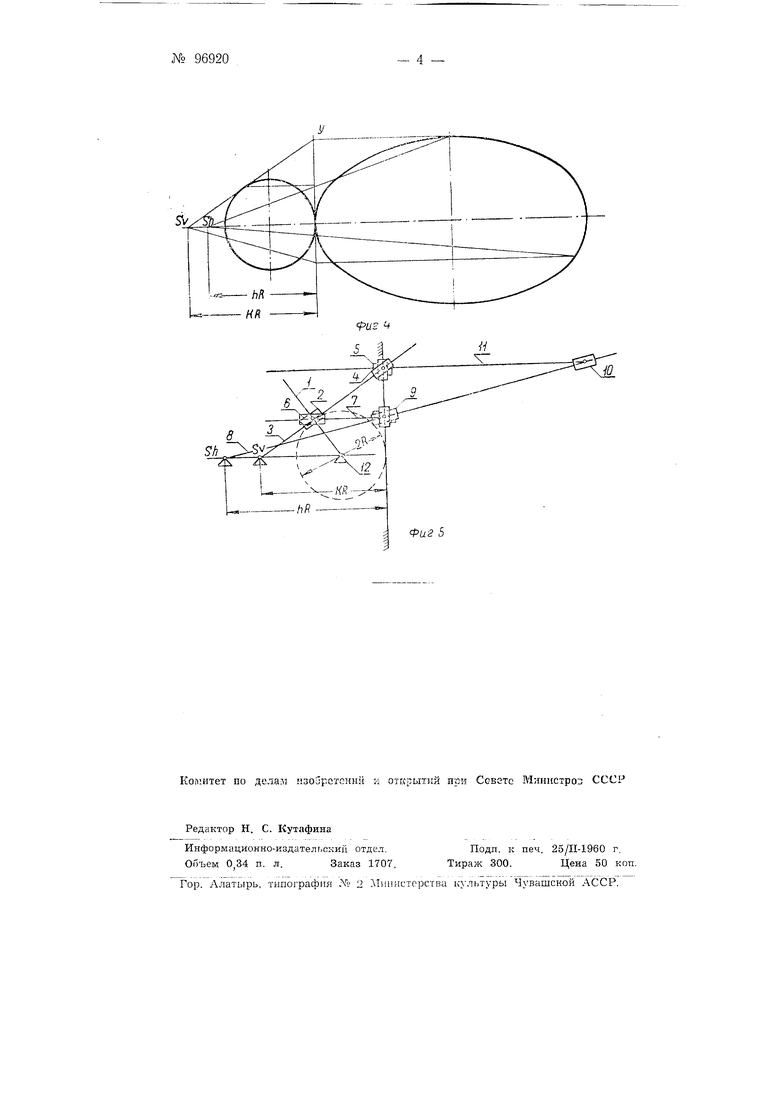
Если на фиг. 1 совместить плоскость V с плоскостью Н, вращая ее против часовой стрелки, то изображение окружности и эллипса будут лежать в одной плоскости (фиг. 4), причем каждой точке окружности соответствует точка на эллипсе. Па совмещенных плоскостях Н и V точка полюса S имеет две проекции: горизонтальную Sh - на расстоянии hR и вертикальную Sv- на расстоянии KR от начала координат Y.
Предлагаемое устройство в точности воспроизводит описанное графическое построение конического сечения из окружности методом проекционного преобразования по фиг. 4 на совмещенных плоскостях. Оно представляет собою плоский многозвенник 1 -12 (фиг. 5) с одной степенью свободы. Кривощип 1 заданного радиуса R вращается относительно своей оси 12; две поводковые группы 8 и 3 вращаются относительно центров вращения, расположенных в точках проекции Sh полюса на горизонтальную плоскость и проекции Sv полюса на вертикальную плоскость, совмещенную с горизонтальной плоскостью. Поводковые группы 3-2-4 и 8-9-10 шарнирно связаны между собою и кривошипом 1 звеньями 7 и 11, перемещаемыми по направляющим 6 и 5 параллельно линии, соединяющей центры вращения Sv и Sh. Чертящее приспособление расположено на звене 10, соединяющем поводок 8 со звеном 11. При вращении кривошипа оно вычерчивает кривую второго порядка, размеры которой зависят от положения полюса S, т. е. от величин KR и hR. Изменяя величины К, h и R, можно изменять как параметр конического сечения, так и его вид (эллипс, парабола, гипербола). Шарнирные звенья 4-5 и 9 перемещаются от направляющей, нерпендмкулярной к линии центпов вращения.
Предмет изобретения
Устройство для построения различных кривых второго порядка, состоящее из плоского многозвенника с одной степенью свободы, отличающееся тем, что, с целью применения проекционного преобразования окружности путем изменения положения полюса в различные кривые второго порядка, оно выполнено в виде кривошипа заданного радиуса, вращаемого относительно своей оси, и двух поводковых групп, вращаемых относительно центров вращения, расположенных в точках проекций полюса на горизонтальную плоскость и вертикальную, совмещенную с горизонтальной плоскостью, и щарнир1Ю связанных между собою и кривошипом звеньями, перемещаемыми по направляющим параллельно линии, соединяющей центры вращения.

| название | год | авторы | номер документа |
|---|---|---|---|
| Прибор для воспроизведения эллипса и гиперболы | 1980 |
|
SU901069A1 |
| Прибор для построения сопряженийдугАМи КРиВыХ | 1979 |
|
SU848377A1 |
| УЧЕБНЫЙ ПРИБОР ПО ПЕРСПЕКТИВЕ | 2005 |
|
RU2290699C1 |
| СПЕЦИАЛЬНЫЙ ВЗАИМОЗАМЕНЯЕМЫЙ ПРОФИЛЬ | 1998 |
|
RU2136406C1 |
| ЗЕТОВЫЙ ПРОФИЛЬ | 1998 |
|
RU2135308C1 |
| ДВУТАВРОВЫЙ ПРОФИЛЬ | 1998 |
|
RU2136405C1 |
| Прибор для вычерчивания кривых 2-го порядка | 1976 |
|
SU682395A1 |
| РЕЛЬС | 1998 |
|
RU2136408C1 |
| Шарнирно-рычажный механизм гомологического преобразователя | 1981 |
|
SU962019A1 |
| Прибор для вычерчивания кривых второго порядка | 1961 |
|
SU141315A1 |

Фиг 5
Авторы
Даты
1954-01-01—Публикация
1951-02-14—Подача