Изобретение относится к швейному производству, а также может быть использовано в кожевенном производстве для раскроя цельнокроенных деталей из ткани или кожи1
Известен способ построения и раскроя цельнокроенных деталей одежды заключактийся в там, что определяют контуры детали в развернутом виде с .последующим вырезанием.
При этом шаблон, изготовленньЕй по детали, укладывают на сетку - кан,ву, Конту1ж шаблона, состоящего из частей, последовательно огибают сеткой-канвой « на нее перечерчивают открытые контуры детали. Затем сетку укладывают на миллиметровую бумагу и резцом переводят контуры цельнокроенной детали ClJ.
Однако данный способ трудоемок, дает значительные погрешности и йе позволяет решить вопрос автоматиза- -. цин процесса констоуиоования цельнокроенных деталей с помсхцью ЭВМ.
Г сЦёль изобретения - повышение точности раскроя детали и производительности.
Для достижения цели готовую деталь, сло}|кенную и отформованную по формообразуюсцнм сгибам, или шаблон, по то ряюший форму детали и с предварительно нанесенными на него линиями, соответствующими направлениям продольных я лоперечных нитей и открытых контурах, в сложенно - детали, укладывают в плоскости координат так, чтобы
10 нить, совпадающая по направлению в верхнем и нижнем слоях детали, или соответствующая ей линия на шаблоне совмещалась с осью абсцисс, а линия формообразующего сгиба проходила че15рез начало координат, затем фиксируют контур сложенной детали и ее открытые контуры или шаблон, после чего линию формообразующего сгиба разбивают на элементарные отрезки, на20ходят их проекции на оси координат и с учетом этих определяют истинную длину продольных и поперечных нитей в-развернутой детали.
При этом истинную длину продоль25ной нити в развернутой детали при расположении продольных нитей в ело женной детали равностояишми от линии формообразующего сгиба, а поперечных параллельно оси абсцисс определяют
30 по.уравнению , Детали . гдеф2(У) - уравнение: линии формообразующего сгиба, затем полученную длину отрезка отклгщывают по оси ордииат от ее начала, через конец его проводят линию параллельно оси абсцисс, на ней откладывают величину, соответствующую истинной длине поперечной нити в развернутой детали, которую определяют по уравнению V - V детали , Ч. где Х - проекция отрезка линии открытого контура детали или шаблона; X - проекции отрезка линии формообразующего сгиба. Причем истинную длину продольной нити в развернутой детали при расположении сложенной детали или шаблона в плоскости координат так, что на
детали где ф (Y) - уравнение линии формообразуюо1его сгиба J хГф (Y)l- проекция отрезка линии формообразующего сгиба хГф (Y)1- проекция отрезка линии L ад J открытого контура дета ли или шаблона, о при этом, истинную длину поперечной нити, расположенной на участке выше линии формообразующего сгиба, ограниченном осью ординат, в развернуто детали определяют по уравнению Фм() детали ,где Фгс.() - уравнение линии формообразующего сгцба. а истинную длину продо ной нити в развернутой детали определяют по уравнению АгФади) г -N -Ч Aeтa м 1ж 2аЦгде Y - проекция отрезка линии открытого контура детгши, расположенного вьвие линии формообразующего сгиба.
Г dТ
иШФооСШ
г d5l.
) участке между одним открытым контуром и осью ординат продольные и поперечные нити параллельны осям координат, а на участке между осью ординат и формообразующей линией сгиба, формообразующей линией сгиба и другим открытым контуром детали или шаблона нити наклонены под углом друг к другу, определяет по уравнениюI N| -м о ) , ™ Д« проекция отрезка линии формообразукнцего сгиба на ось ординат; уравнение линии формообразующего сгиба, а истинную длину поперечной нити в развернутой детали определяют по уравнению в детали или шаблоне с криволиней-, ной осью, соответствующей направлению продольных нитей в сложенной детали и расположенной на участке между осью ординат и линией формообразу клпего сгиба, истинную длину поперечной и продольной нитей определяют так, что криволинейную ось и линию формообразующего сгиба разбивают на отрезки и находят проекции этих отрезков на оси координат, которые учитывают при определении истинной длины продольной и поперечной нитей в развернутойдетали, при этом истинную длину продольной нити в развернутой детали определяют по уравнению () Аетаки1 Г... ( ;U....,) где д Х- - проекция элементарного отрезка линии формообразующего сгиба на ось абсцисс} 4vYj,g - проекция элементарного отрезка линии формообразующего сгиба на ось ординат ; проекция элементарного отрезка криволинейной оси на ось абсцисс; - проекция элементарного отрезка криволинейной оси на ось ординат.
а истинную длину поперечной нити
/uXjft П/дхзгУ .ЭДГ(Ти1
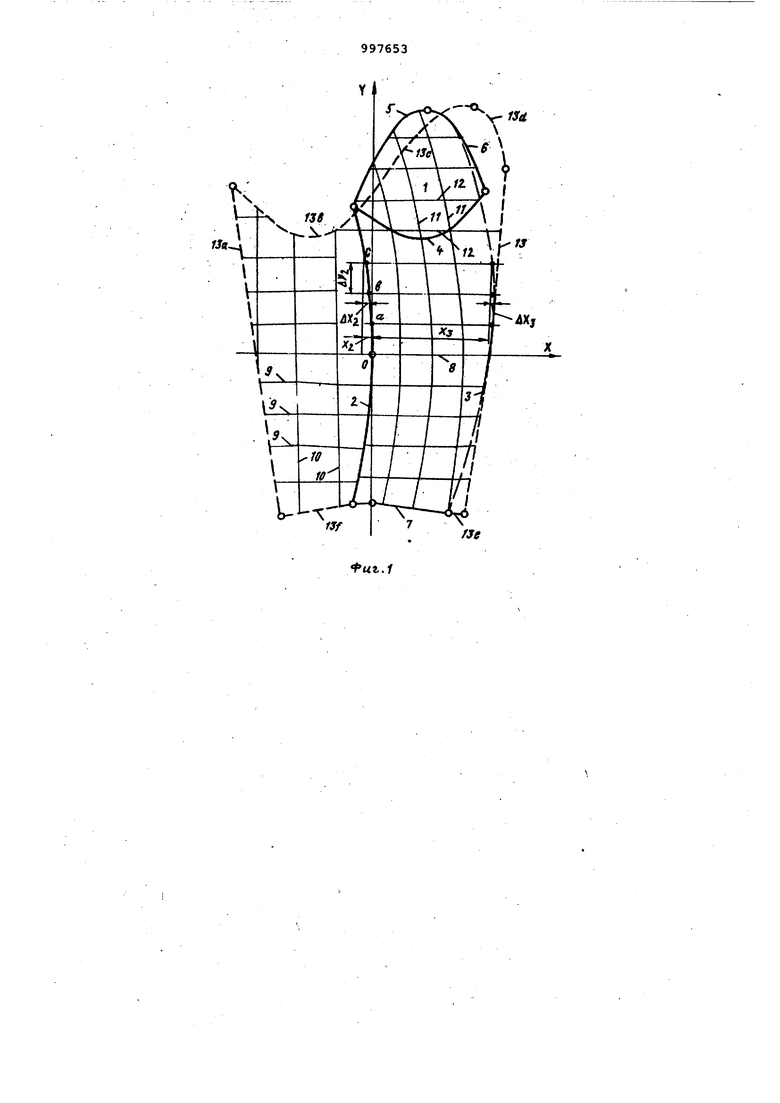
те,л л / та1Ш« & iJl b:iae./ J где Д.Х2В AYjg, проекции элементард)01 AVgp його отрезка линии формообразующего сгиба и открытого контура детали или шаблона на ось абс .цисс и ординат, , п 1, 2, 3 ..., ДХ.р, ДХ(9 - проекции .элементарного отрезка криво. линейной оси на ось абсцисс иординат. На фиг. 1 изображена схема постро ения детали рукава в развернутом видеУ на фиг. 2 - схема построения изменения гёок1етрии ткани в сложенной детали i построение контура этой Детали в развернутом виде; на фиг.3 схема построения изменения геометрии ткани элемента сложенной детали; на фиг. 4 - cxieMa построения изменения геометрии ткани в сложенной детали воротника и построение его контура в развернутом виде; на фиг. 5 - схема построения изменения геометрии ткани элемента сложенной детгши воротника и построение элемента его контура в развернутом виде; на фиг,6 схема построения контура детали воротника/ цельнокроенного со стойкой в развернутом виде. Способ построения и раскроя цельнокроенных деталей одежды заключается в том, что шаблон 1 .(фиг. 1) детали, например рукава, изготовленный по сложенной и отформованной по формообразующим сгибам 2 и 3 и нанесеннамя на него бткрытьвт контурами 4-7 или готовую деталь, сложенную и отформованную по формообразующим сгибам 2 и 3 и. вьтолнякхпую роль шаблог на, укладывают в плоскости координат ХОУ. При этом нить 8, совпсьдающую по .направлению в верхнем и нижнем слоях детали, или линию 8,i соответствующую ей в шаблоне, совмещают :.с осью абсцисс, а одна из линий формообразующего сгиба, например 2 проходит через начало координат. Контур шаблона I или сложенную деталь и ее открытые контуры фиксируют, в 4астнЬсти обводят на плоскости ХОУ. Затем линию фор.мообразующего сгиба 2 разбивают на эл«1«юнтарные отрезки оа, аЬ, Ье с постоянным шагом. Находят их Провернутой детали определяют по уравнению
i 2
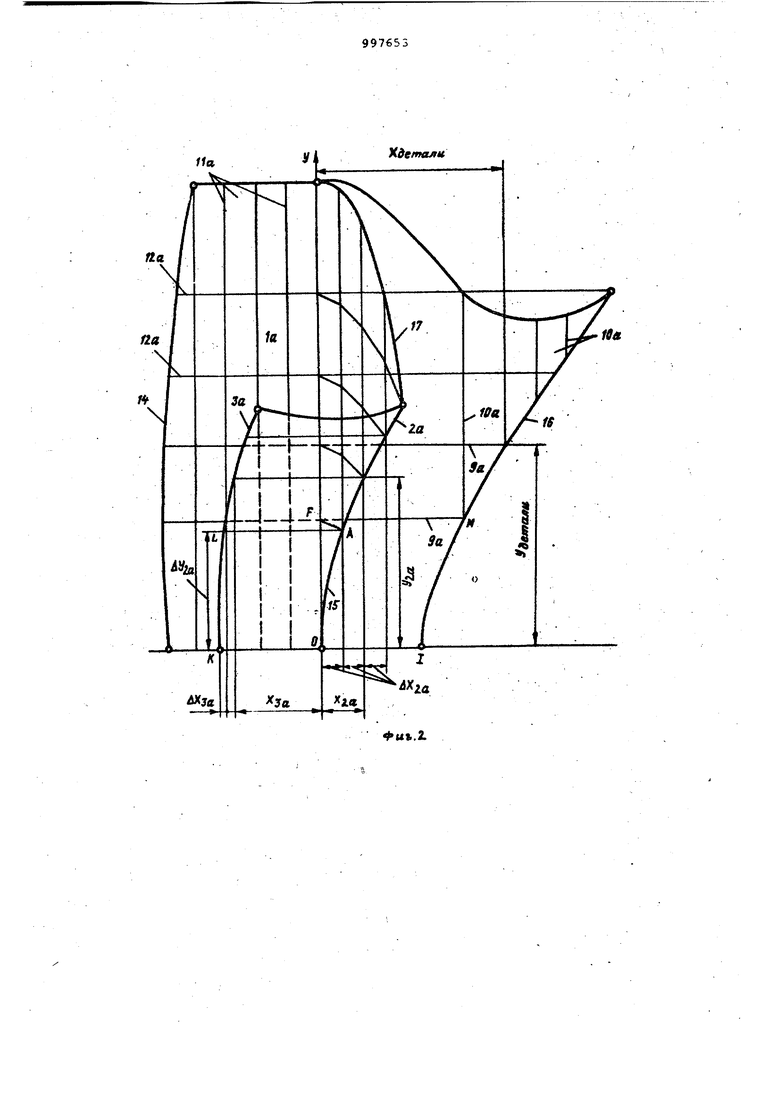
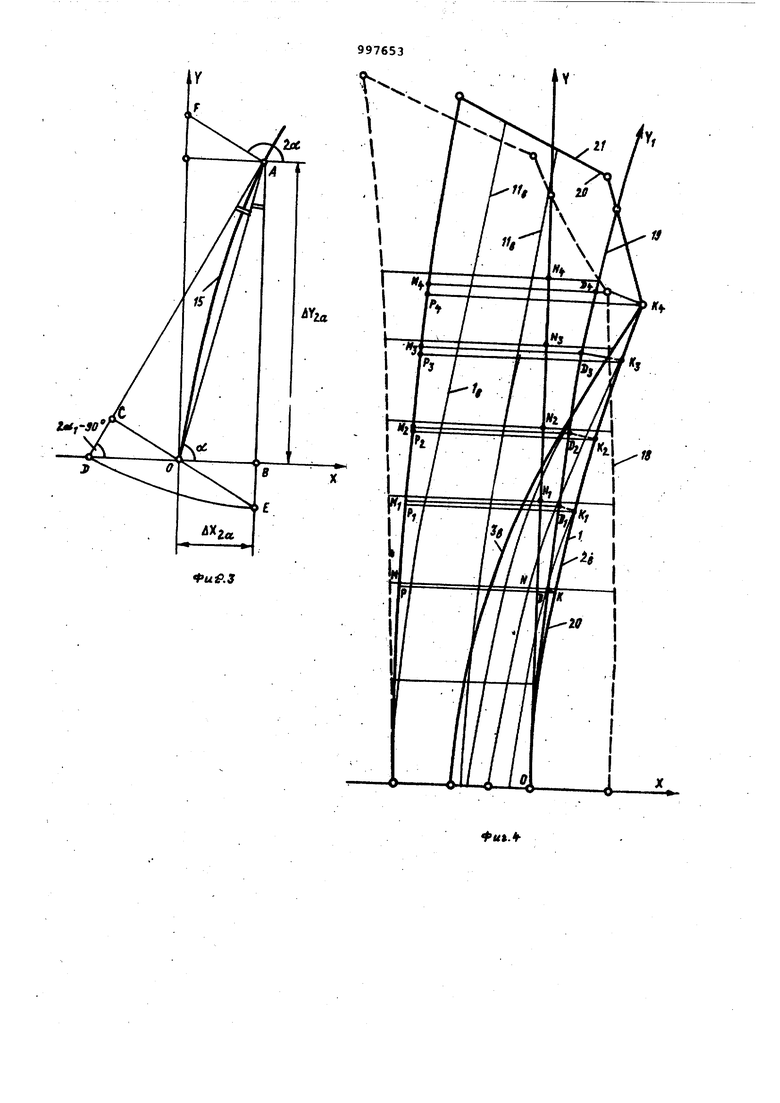
WxW екции , .на оси координат и с учетом этих величин по зависимостям определяют истинную длину поперечных 9 и продольных 10 нитей. От точки О по оси ординат откладывают найденные длины продольных нитей 10, которые одновременно определяют и положение поперечных нитей 9 относительно оси абсцисс. Из концов полученных на оси ординат отрезков проводят прямые, параллельньае оси абсцисс, и на них откладывают истинную длину роперечных нитей 9. При этом истинную длину поперечных и продольных нитей можно определить двумя методами: графичесКИМ или расчетным. Соединяя полученные точки.определяют истинный контур развернутой цельнокрденной детали. Рассмотрим расчетный метод получения контураразвернутой це льнокроенной детали, если в сложенной детали 1 продольные нити 11 равноотстоят от линии формообразугомего сгиба 2 (фиг. 1), а поперечные нити 12, расположены параллельно оси абсцисс. Линию формообразующего сгиба 2 и линию другого формообразукмцего сгиба 3, которая в данном случае является и контуром детали или шаблона, разбивают на элементарные отрезки (фиг. 1), Находят проекции этих отрезков на оси координат и с их учетом определяют истинную длину поперечных нитей 9 и длинУ продольных нитей 10. При этом (фиг. 1) истинную длину поперечных нитей 9 в развернутой де- , тали, равную длине поперечных нитей 12 в сложенной детали, можно опре- . делить по зависимости Аетал«-| )а. .. л-1,4Лгде Л Х - проекция элементарного отрезка линии другого формообразующего сгиба 3 или маблоиа на ось абсцисс;. UX 2 - проекция элементарного отрезка.линии формообразующего сгиба 2 на Ось абсцисс, или VeTQAw h г . где Х - проекция отрезка линии другого формообразующего сгиба 3 детали или шаблона/ X - проекция отрезка линии фор мообразующего сгиба 2. Из анализа изменения геометрии ткани (фиг. 1) в сложенной детали видно, что для нахождения длины про дольных нитей 10, определякядих такж положение поперечных нитей 9 в развернутой детали относительно оси абсцисс, необходимо ийпольэовать уравнение. етали--| ): У«-1,2Д... где Л-Х. , M,i - проекция элементар ного отрезка линии формообразующего сгиба 2 на оси коор динат ; где Ф(У) - уравнение линии Формооб разующего сгиба 2. В случае, если поперечные нити 12 в .сложенной детали прямолинейны наклонены к положительному.направле нию оси ОХ под углом ЗГ 180- fb , контур развернутой детали 13 получа .ют аналогичным путем. При этом длин поперечных 9 и продольных нитей 10 получают по зависимостям, приведенным выше, но уравнения линии формообразующего сгиба 2 и открытых конт ров детали или.шаеЗюна должны быть заданы в новых осях координат, пове нутых по отношению к исходным на угол У 180°- р . Рассмотрим графический метод построения контура развернутой цельно кроенной детали при расположении сл женной детали 1а (фиг, 2) или шабло в плоскости координат так, что на участке между открытым контуром 14 и осью ординат продольные 11а и поперечные 12а нити параллельны осям координат, а на участке меясду осью ординат и линией формообразующего сгиба 2а, линией формообразующего сгиба 2а и открытым контуром За детали или шаблона,- нити наклонены под углом друг к Д|эугу. Линию формообразующего сгиба 2а раз 5ивают на элементарные отрезки с постоянным приращенным независимо переме нной UXjo . Выделяют элемента ный отрезок 15-ОА линии формообразу ющего сгиба г:а (фиг. 2 и 3) , ,Он определяется проекциями АХ2а.АТл.аИ наклонной под углом об к положитель ному направлению оси ОХ. На выбранном элементарном отрезке 15-ОА (фиг. 3) как на диагонали строят па раллелограмм,. Для этого треугольник ОНА поворачивают вокруг ОА и находят точку С, симметричную точкт В. Затем продолжают линию АС до пересечения с осью ОХ в точке D. Пользуясь допущением о неизменности длин нитей, находят положение точки D на направлении прямой АВ. Для этого из точки А радиусом AD описывают дугу до пересечения с продолжением вертикали АВ в точке Е. Дополняя ОЕА до параллелограмма, находят искомое направление элемента нити на участке между осью ординат и линией формообразующего сгиба 2а - напра вление AF. Для элементарной полоски ткани шириной AXj угол наклона отрезка AF, равный 2oL , од:.рзначно определяет направление всех остсшьных нитей на участке между осью ординат и линией формообразующего сгиба 2а, расположенных вырле отрезка AF. Угол наклона 2ct- 90° отрезка AD однозначно определяет направление нитей элементарной полоски fkaHH высотой на участке между линией формообразующего сгиба 2а и открытым контуром За детали или шаблона (фиг. 2). Для построения контура 16 развернутой цельнокроенной детали от точки О вправо отклс1дывают отрезок 01, равный ртрезку ОК (фиг. 2). Точка 1 начальная точка развертки. Затем из точки F пересечения стороны первого параллелограмма с осью OY проводят прямую, параллельную оси ОХ. На ней последовательно откладывают отрезки FA, AL, равные соответствующим сторонам параллелограммов. Получают точку М контура 16.. Аналогичными построениями определяют положение других точек линии 16. Соединяя их плавной кривой„ получают искомый контур 16 развернутой цельнокроенной детали.. Контур 16 развернутой цельнокроенной детали можно сразу построить по зависимостям, полученным на основе приведенных графических построений. Для элементарного отрезка. ОА линии формообразующего сгиба 2а приращение истинной длины поперечной нити 9а, проходящей в сложенной детали 1а или шаблоне через точку А (фиг. 2 и 3), определяют как Уго .у cos080-2ot) Положение нити 9а относительно оси абсцисс или истинную длину элемента, продольной нити (фиг. 3) определяют как ОС - Мао+ АХ2с| ч(180-2Л}
Истинную дпину поперечной нити определяют по уравнению
VI
детали
,2,...
ограниченном осью ординат, в развернуто детали определяют по уравнению








| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПОСТРОЕНИЯ ШАБЛОНА ВОРОТНИКА | 2005 |
|
RU2295899C1 |
| НОСОВАЯ ЧАСТЬ ФЮЗЕЛЯЖА | 2008 |
|
RU2403174C2 |
| Способ получения объемной формы подушки пресса для влажно-тепловой обработки швейных изделий | 1978 |
|
SU994593A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОМПЛЕКСА ПАРАМЕТРОВ ПОПЕРЕЧНОГО СЕЧЕНИЯ ТЕЛ КВАЗИЦИЛИНДРИЧЕСКОЙ ФОРМЫ | 2016 |
|
RU2645002C2 |
| СПОСОБ ТОЧНОГО КРОЯ | 2004 |
|
RU2264143C2 |
| СПОСОБ ИНЕРЦИАЛЬНЫХ ИЗМЕРЕНИЙ НЕРОВНОСТЕЙ РЕЛЬСОВОГО ПУТИ | 2002 |
|
RU2242391C2 |
| ФОРМУЮЩЕЕ УСТРОЙСТВО, МАШИНА, УПАКОВОЧНОЕ ЛАМИНАТНОЕ ПОЛОТНО, СПОСОБ И ПРОЦЕСС ФОРМОВКИ В ПРОИЗВОДСТВЕ УПАКОВОЧНОЙ ТАРЫ | 2007 |
|
RU2416553C2 |
| СПОСОБ АВТОМАТИЧЕСКОГО ОПРЕДЕЛЕНИЯ И КОРРЕКЦИИ РАДИАЛЬНОЙ ДИСТОРСИИ НА ЦИФРОВОМ ИЗОБРАЖЕНИИ | 2006 |
|
RU2351091C2 |
| Способ получения развертки поверхности манекена | 1980 |
|
SU925302A1 |
| СПОСОБ НЕПРЕРЫВНОГО ПОЛУЧЕНИЯ ПРОФИЛИРОВАННЫХ КРИСТАЛЛИЧЕСКИХ ИЗДЕЛИЙ ИЗ РАСПЛАВА | 1990 |
|
SU1820638A1 |

отрезка линии формообразующего сгиба 2а на ось ординат; . ЛХ2а- проекция элементарного отрезка линии формообразующего сгиба 2а на ось абсциссJ ЛХ,- проекция элементарнс о отрезка открытого контура детали или шиблона на ось абсцисс, г л-«г }Л Аетали Ч м М Ч где ,()3- проекция отрезка пиНИИ формообразуюо1его сгиба 2а/ ,(У)- проекция отрезка лиНИИ открытого KOHiypa За детали или шаблона (У) - уравнение линии формообразуюцей сгиба 2а Истинную длину продольной нити 10а в развернутой детали определяют по уравнению Х, , проекции, элементарного отрезка линии фсфмообразуквдего сгиба 2а, .у жМ)н АГГОАИ |гФаа«)) - уравнение линии фоЪмооб разующего сгиба 2а. тинну1ч дпину продольной нити том случае определяют уравмг| у-и fASaaf . и М.4...
или
М. - проекция элементарного отрезка линии открытого контура детали или шаблона, расположенного выше линии формообразующего сгиба,
у-.
Аетш 2а гй
4is4
проекции элементарного отрезка линии формообразующего сгиба 2а на оси координат/
уравнение линии формообразующего сгиба 2а.
поперечной нити, участке вьше линии сгиба 2а (фиг. 2),
--М oV
Детали п J
11г Нгде Y - проекция отрезка линии ; открытого контура детали или шаблона; расположенного выие линии формообразующего сгиба.
В случае, если на участке между линией формообразующего сгиба 2а и открытым контуром За детали или шаблона поперечные нити в сложенной дег тали прямолинейны и наклонены к полс| жительному направлению оси абсцисс под углом У , то положение точек линий I
feMLM-V
Vt
-L
ли t
,a,.
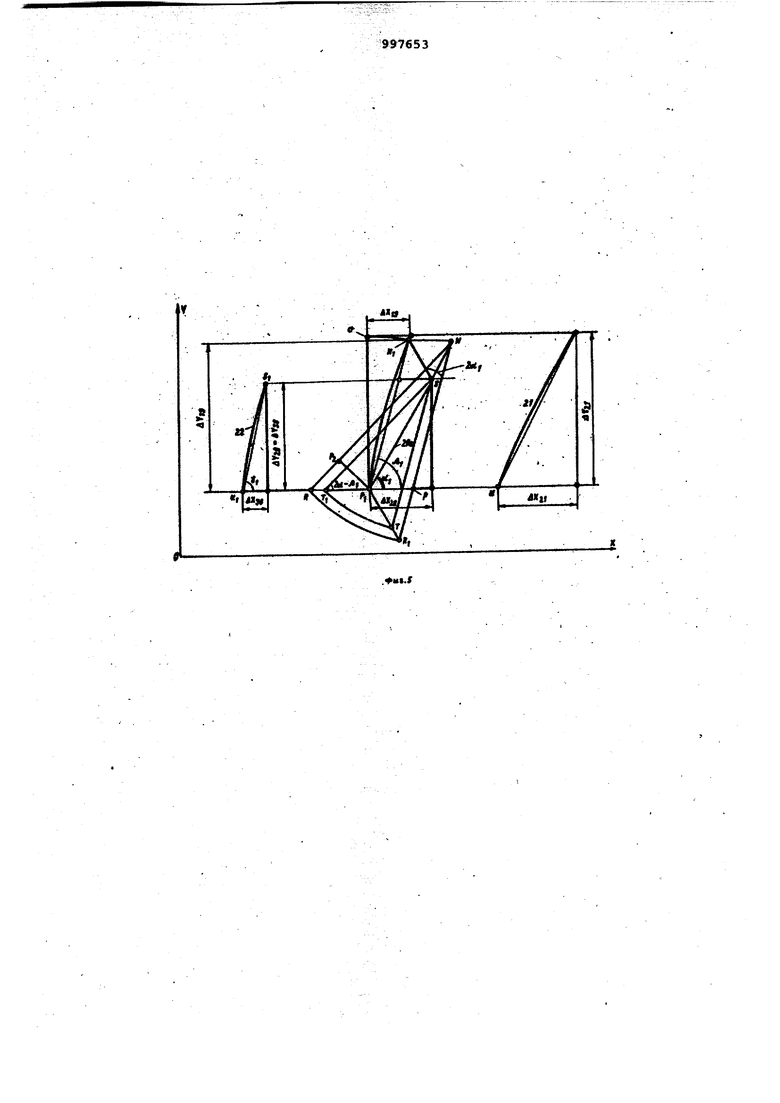
L UQпроекции элементарного отрезка линии формообразующего сгиба 2а на оси координат;й.Х fiY - проекции элементар ного отрезка открыто го контура За детали или шаблона. Рассмотрим графический метод построения контура 18 (фиг. О детали 16, например, воротника или шаблона ife с криволинейной осью 19, соответствукмдей направлению продольных нитей 116 в сложенной детали и расположенной на участке между осью ординат и линией формообразующего сгиба 2Ь. Криволинейную ось 19 и линию формообразующего сгиба 2fe разбивают на элементарные отрезки с постоянным приращением. Выделяют элементарный отрезок 20 линии формообразующего сгиба 24 (фиг,о4 и 5). Спрямленный отрезок 20а (фиг. 5) наклонен под углом oL к положительному направлению оси абсцисс. На выбраннсш спрямленном отрезке 20а (фиг, 5) как на диагонали строят параллелограмм. Для этого из точки N конца элементарного отрезка 20а проводят прямую NP, параллельную соответствующему спрямленному участку N Р. криволинейной оси 19. Полученный треугольник поворачива ют вокруг отрезка NP, . Отрезок NP продолжают до пересечения с прямой, параллельной оси ох в точке R. Из точки;, TJ радиусом NR описывают дугу до пересечзния с продолжением прямой NP в точке f. Точку R соединяют с точ кой I. . Из точки N проводят прямую N S параллельно Р Я. Направление отрезка N S - направление элемента поперечной нити в сложенной детали It на участке между осью 19 и линие формообразующего сгиба 2Ь. Треуголь ник Р N 5 дополняют до параллелогра ма: проводят прямую ST параллельно . Затем определяют положение то ки т на прямой, проведенной из точк Р параллельно оси абсцисс, получают точку Т Для элементарной полоски
,
t«ib-i
йХад I J контура раввёрнутой дета- - . - I .Т леталио определяют по уравнениям I ткани высотой угол наклона Зэ| р|.| трёзка ST,( однозначно определяет направление продольных нитей на участке сложенной детали 1-6 (фиг. 4) между линией формообразующего Сгиба 2-6 и открытым контуром 3-8. Угол наклона 2о( отрезка однозначно определяет направление всех остальных поперечных нитей элементарной полоски ткани шириной участке между криволинейной осью 19 и линией формообразующего сгиба 2ft. При пост)рении выделяют элементар1ый отрезок 2Q элемента 21 контура 18 развернутой цельнокроенной детали на прямой, проведенной из точки начала элементарного отрезка 20а, откладывают отрезок ), равный отрезку Р и . Затем из этой же точки Р на прямой, проведенной параллельно оси ординат, откладывают отрезок PxfV, равный по величине отрезку . Из полученной точки V проводят прямую параллельно оси абсцисс. На ней .последовательно откладывают дпины отрезков N S , SS . Полученные точки начала и концы элементарного отрезка 20 линии контура 21 развернутой цельнокроенной детали соединяют. Аналогичными построениями получают остальные точки линии контура 18 развернутой цельнокрренной детали. Линию контура 18 можно получить расчетным методом по зависимостям, выведенным ria осно.ве приведенных графических построений. Для элементарного отрезка 20 линии формообразующего сгиба приращение йХ истинной длины попервчно й нити, проходя щей через точку S конца элементарно.го отрезка 20, определяют по уравнениюду .дУйй5НнСУ 1- 1) . ду C03«l 5iv(,)a6 Щ где d г угол наклона элементарного отрезка 20 линии формообразующего сгиба;
угол наклона элементарного отрезка Р М( криволинейной оси 19,
угол наклона элементарного
отрезка 22 открытого контура 34 детали или шаблона
йХгьГ.(Мэв(Д1Ц1 и Ш1Г/ЛЗ М
и
«Т
Аеюлм
р,а,.
проекции элементарного отрезка линии формообразующего сгиба 24; проекции элементарного отрезка открытого контура 34 детали или шаблона t - проекции элементарного отрезка криволиней ной оси 19. истинную длину элементаного отрез ка продольной нити llS, соответстII I I м -ч- 1 и детоки - Ад...|Н А)С-, - проекции элементарного отрезка линии формообразующего сгиба 2Й; дУ - проекции элементар. ного отрезка, криволинейной оси 19. П р и м е р. Определим истинную длину продольных иитей 9 и поперечных нитей 10 (фиг.. 1) в развернутой детали/ рукава, если в сложенной детали рукава 1 продольные нити 11 рав ноотстоят от линии формообразующего сгиба.2, а поперечные нити 12 распог ложены параллельно оси абсцисс. Пусть в системе координат XOY лииия формообразующего сгиба рукава 2 описывается уравнением }( 100 -V 100 Y , линия другого формообразуищего сгиба рукава 3 X, « ---ВО + VIOOZ . (у-12) линия оката Х4 - 7 -/15б,25 - (Y-32 Xg - V389 - + 9, Х 0,93 V389 - 10Y + 9, линия низа Х-, « --7,7Y -Ь 187,7. Используя приведенные зависимости для этого случая, получаем истинную длину поперечных нитей в развернутой J л,- .X-f,g« -( Х)«, детали Х. X л-.х,); х Ч- V . л . Хлал Х « Xjir - IХ X, N36 г Nbf
А X - проекция элементарного отрезка 20 линии формообразующего сгиба 28.
В общем виде истинную длину поперечной нити в раэве{жутой детали определяют по уравнению )П.эв wJLUViJ j
a
le
J4i.
.f
1
) ) 4JV
(вующую положейию поперечной нити носительно прямой, проходящей через точку Kf , начала элементарного отрезка 20, определяют из .
A lft-t d
A.,,P,0--P,s
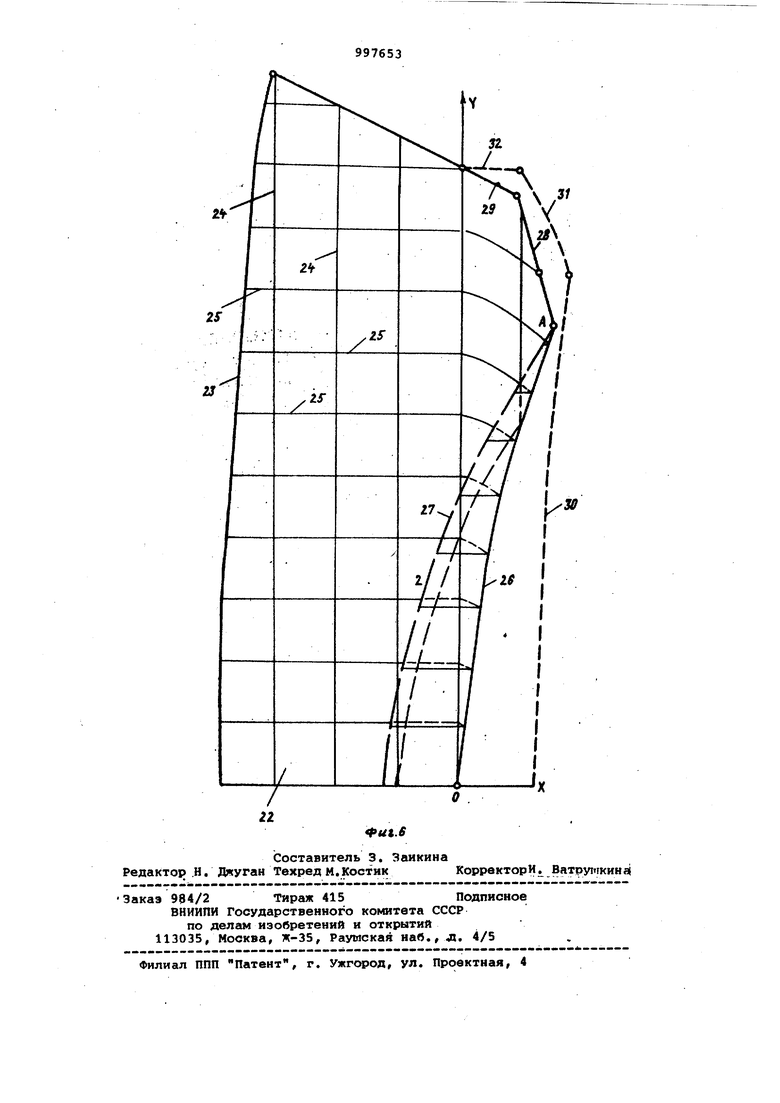
20 Ы ,Ч Следовательно, в общем виде положение поперечной нити относительно оси абсцисс можно определить по уравнениюЖШ1. ШЧ) 1 Истинная длина продольных нитей Истинная длина пр определяется для всех контуров развернутой детали по одному уравнению 100 arcstn детали Определим истинную длину продольных и поперечных нитей в развернутой детали воротника 22, цельнокроенного со стойкой (фиг. 6), если при расположении сложенной детали в плоскости координат на участке между линией отлета воротника 23 и осью ординат продольные 24 и поперечные 25 нити параллельны осям координат, а на . участке между осью ординат и линией формообразунадего сгиба 26, линией формообразующего сгиба 26 и срезом стойки 27 - нити расположены под углом друг к другу.. В системе координат XOY контуры обведенной детали или шаблона данно- го воротника описываются уравнениями ,0.,01V-2,60; ,Cf) 6,30, X,,,i Истинную длину продольных и поперечных нитей в развернутой детали воротника цельнокроенного со. стойкой определяют по приведенным .зависимостям для этого случая. Тогда Ь |2066-)-Н-349,(4; М - 0 лг/1ев, lj+0. I ,45tH| p - :j5S|; Х, ,4183,50-X-7n3ieH)d6 k66-X|; ,30X 76,28Vx--72 7,5ev, И9. л - -«- r-r- - I fQft7 in Н91р7-УхР -o,465X47t,a 8- -7ПЪъеу | |t03Hi j 49.07-Ух Истинную длину продольных и поперечных нитей в развернутой детали воротника, цельнокроенного со стойкой (фиг. 4), при Нсшичии криволинейной оси, соответствующей направле ВИЮ продольных нитей в сложенной детали и расположенной на участке межд осью ординат и лннией сгибг 2 (фиг. 4), определяют на ЭВМ по приведенным зависимостям для данного случая. Формула изобретения 1.Способ раскроя цельнокроенных деталей одечсды, заключающийся в том, что определяют контуры детали в развернутом виде с последующим их вырезанием, о т л и ч а ю щ и й- с я тем что, с целью повы1:вения точности раскроя детали и производительности, готовую деталь, сложенную и отформованную по формообразующим сгибам, или шаблон, повторяющий, форму детали и с предварительно нанесенными на него линиями, соответствующими направлениям продольных и поперечных нитей и открытых контуров в сложенной детали, укладывают в плоскости координат так, чтобы нить, совпадающая по направлению в верхнем и нижнем слоях детали, или соответствующая ей линия на шаблоне совмещалась с осью абсцисс, а линия формообразующего сгиба проходила через начало коорд шат, затем фиксируют контур сложенной детали и ее открытые конту ры или шаблон, после чего линию формообразующего сги«а разбивают на эле ментарные отрезки, находят их проекции на оси координат и с учетом этих величин определяют истинную длину продольных и поперечных нитей в развернутой деагши. 2.Способ по п. 1, о т л и ч а-. ю щ и и с я тем, что истинную длину продольной нити в развернутой детали при расположении продольных нитей в сложенной детали параллельно линии формообразукмцего сгиба, а поперечных параллельно оси абсцисс определяют по уравнению Аетали И ЧЬ С)а). где (Y) - уравнение линии формообразующего сгиба, затем полученную длину откладывают по оси ординат от ее начала, через конец его проводят линию параллельно оси абсцисс, на ней откладывают величину, соответствующую истинной длине поперечной нити в развернутой детали, которую определяют по уравнениюдетали где X - проекция отрезка линии открытого контура детали или шаблона, X - проекции отрезка линии формообразующего сгиба. 3. Способ по пп. 1 и 2, отличающийся тем, что истинную длину продольной нити в развернутой детали при расположении сложенной детали или шаблона в плоскости координат, так, что между осью ординат и отрицательным нап{ авлением оси абсцисс продольные и поперечные нити параллельны осям координат, а в плоскости между осью ординат и положительным направлением оси абсцисс наклонены под углом относительно оси абсцисс, определяют по уравлению Г 61 .рГ ,ди Детали 10 J -LaTao J где Ygig- уравнение линии формообразующего сгиба, а Истинную длину поперечной нити в развернутой -детали, определяют по vpaвнeнию AeTOAH tq aoiv)xtq, где (Y) - уравнение линии формообразующего сгиба, x fejjg(Y)3- проекция отрезка линии формообразующего сгиба, (Y)- проекция отрезка линии открытого контура детали или шаблона.
при этом истинную длину поперечной нити в развернутой детали, расположенной на участке выше линии формообразующего сгиба и ограниченном осью ординат, определяют по уравнению
d,
детопи )tгдеф {Х) - уравнение линии формообразующего сгиба,
а истинную длину продольной нити в развернутой детали определяют по уравнению
м-У)
т1
-ах, WTOKM проекция элементарного отрезка линии фсч мообра-. зуюцего сгиба; проекция элементарного отрезка линии формообразувяцего сгиба; Приорите 05.07.76. Источн
где Y - проекция отрезка линии открытого контура лётаяи, расположенного suite линии формообразующего .сгиба. 4. Способ по пп, 1-3, о т л.ичающийся тем, что определяют дополнительную криволинейную ось в плоскости координат, соответствующую направлению продольных нитей в сложенной детали и расположенную на
0 участке межЯУ положительным направглением оси ординат и линией формообразующего сгиба, затем дополнительную ось и линию формообразукщего сгиба разбивают на отрезки н находят
5 проекции этих отрезков на оси координат , которые учитывают при определении истинной длины продольной и поперечной нитей в развернутой детали, при этом истинную длину продольной нити в развернутой детали определяют
0 по уравнению 35 ,(.(Л J детали т по пунктам: по п..4. ики информации, - проекция элементарного отрезка криволинейной .оси У AXfp - проекция элементах ного отрезка криволинейнойоси а истинную длину поперечной нити в;развернутрй детали определяют пр уравнению , . принятые во внимание при экспертизе 1. Авторское свидетельство СССР №255150, КЛ. А 41 D 1/06, 1968.
Гч
ицtyf
13d
fui.l
Хдетаяи
u.2L
Mt.f
Авторы
Даты
1983-02-23—Публикация
1976-04-03—Подача