Изобретение относится к области контрольно-измерительной техники, а именно к способам определения геометрических параметров поперечного сечения тел квазицилиндрической формы, преимущественно саженцев и укорененных черенков садовых культур для оценки их качества.
При выполнении селекционных, научно-исследовательских и агротехнических работ в процессах промышленного возделывания садовых культур необходим контроль качества готового продукта (черенков, саженцев). Одними из показателей развитости и качества растений являются геометрические параметры поперечного сечения штамба (для справки, штамб - это надземная часть растения между корнем и первой ветвью): поперечный размер, длина контура, площадь, индекс формы (отношение максимального и минимального ортогональных поперечных размеров).
Известны способы, включающие измерения поперечного размера сечения тела путем совмещения двух базовых точек, расстояние между которыми определяют по шкале (механической или электронной), с соответствующими контрольными точками, расположенными на контуре контролируемого сечения тела. Эти способы реализуются такими контактными устройствами, как штангенциркули и микрометры [ГОСТ Р 53135-2008. Посадочный материал плодовых, ягодных, субтропических, орехоплодных, цитрусовых культур и чая. Технические условия. - С. 38]. Процедура измерений контактными способами и средствами характеризуется высокой трудоемкостью и низкой производительностью. Чтобы получить данные для определения площади поперечного сечения, необходимо вручную измерить множество поперечных размеров сечения в разных направлениях. Кроме того, контакт с поверхностью контролируемых садовых культур осуществляют с определенным измерительным усилием, что приводит к деформации контролируемых объектов и, как следствие, к погрешностям измерений из-за изменения размеров объекта. Поэтому более предпочтительными для контроля геометрических параметров поперечного сечения подобных объектов являются бесконтактные способы, среди которых известен теневой способ [А.с. №945649, МПК G01B 11/08. Устройство для контроля поперечного сечения объекта / В.К. Александров, В.Н. Ильин, А.Л. Старков. - Заявка №3213753/25-28; Заявлено 08.12.1980; Опубл. 23.07.1982 Бюл. №27]. Сущность теневого способа заключается в том, что диаметр поперечного сечения тела определяют по размерам тени, создаваемой контролируемым телом при освещении его широким тонким пучком света, состоящим из множества параллельных лучей. В данном способе определяют множество диаметров поперечного сечения тела в разных направлениях путем сканирования с помощью системы зеркал. Недостатком способа является сложность его реализации, а также невозможность применения для контроля поперечных сечений, имеющих вогнутые участки. Для таких объектов применим способ, основанный на методе структурного освещения и предложенный КТИ НП СО РАН для контроля поперечного сечения контактных проводов электросети электровозов, трамваев, троллейбусов [Каликин В.Э., Базин B.C., Верхогляд А.Г. и др. Автоматизированная оптико-электронная система измерения износа контактного провода // Оптико-информационные измерительные и лазерные технологии и системы: Юбилейный сборник избранных трудов КТИ НП СО РАН / Науч. ред. Ю.В. Чугуй. - Новосибирск: Академическое изд-во «Гео», 2012. - С. 161-170]. Способ заключается в том, что специальным лазерным осветителем формируют плоский лазерный луч («световой нож»), пересекающий поверхность контактного провода под некоторым углом к его оси. Свет, рассеянный от поверхности провода, детектируют цифровой видеокамерой. Зафиксированное изображение представляет форму кривой, сформированной пересечением плоского луча с поверхностью контактного провода. Недостаток способа - высокая стоимость его реализации. Наиболее близким аналогом изобретению (прототипом) по технической сущности является способ с применением лазерных триангуляционных датчиков расстояний для определения комплекса геометрических параметров поперечного сечения тел квазицилиндрической формы, преимущественно саженцев и укорененных черенков садовых культур [Патент РФ №2551264, МПК G01B 11/08. Способ определения геометрических параметров сечения тела и устройство для его осуществления / В.В. Минеев, В.А. Золотарев, А.Ф. Алейников, В.Б. Морозов. - Заявка №2013144512/28; Заявлено 03.10.2013; Опубл. 20.05.2015 Бюл. №14]. Способ заключается в том, что с помощью двух лазерных триангуляционных датчиков, расположенных с разных сторон от объекта на фиксированной дистанции между собой, измеряют расстояния до контрольных точек на контуре поперечного сечения и определяют длины семейства параллельных отрезков, расположенных на заданном расстоянии друг от друга в плоскости сечения между соответствующими парами контрольных точек, затем по полученным значениям расстояний и длин отрезков определяют координаты всех полученных контрольных точек в прямоугольной системе координат и геометрические параметры поперечного сечения тела: длину контура, площадь и отношение максимального и минимального ортогональных поперечных размеров - индекс формы. Достоинством прототипа является возможность определения комплекса геометрических параметров поперечного сечения тела. Недостатком прототипа является то, что реализация способа требует выполнения измерений до контрольных точек на контуре поперечного сечения тела от двух базовых точек и, соответственно, применения двух лазерных триангуляционных датчиков, что усложняет процесс реализации способа и делает дорогостоящим устройство для его осуществления.
Техническим результатом изобретения является снижение трудоемкости способа определения комплекса геометрических параметров поперечного сечения тела за счет выполнения измерений расстояний до контрольных точек на контуре сечения от одной базовой точки и, соответственно, с помощью одного лазерного триангуляционного датчика.
Технический результат в изобретении достигается тем, что в способе определения комплекса геометрических параметров поперечного сечения тел квазицилиндрической формы, включающем измерения расстояний от базовой точки, расположенной в плоскости контролируемого поперечного сечения на определенном расстоянии от поверхности тела до соответствующих контрольных точек, расположенных на контуре поперечного сечения тела, базовую точку располагают на фиксированной дистанции от центральной точки, находящейся в пределах контролируемого поперечного сечения тела, и осуществляют измерения расстояний от базовой точки до контрольных точек по направлению к этой центральной точке при вращении контролируемого поперечного сечения тела вокруг оси, проходящей через центральную точку перпендикулярно плоскости сечения, начиная от начального углового положения через каждые одинаковые угловые интервалы в пределах одного оборота, затем определяют длины отрезков между центральной и контрольными точками, как разности между фиксированной дистанцией базовой точки от центральной точки и измеренными расстояниями от базовой точки до каждой из контрольных точек, и по полученным значениям длин отрезков и выбранному значению угловых интервалов определяют координаты всех контрольных точек в прямоугольной системе координат и геометрические параметры сечения тела: длину контура, площадь, максимальный и минимальный ортогональные размеры и их отношение - индекс формы, при этом значение угловых интервалов выбирают так, чтобы их число в пределах оборота было целым. Для определения координат контрольных точек центральную точку принимают за начало прямоугольной системы координат, длину отрезка между центральной и контрольной точкой, определенную при начальном угловом положении контролируемого поперечного сечения, откладывают от начала системы координат на оси абсцисс и координаты конца отрезка принимают за координаты первой контрольной точки, координаты остальных контрольных точек получают аналогично путем откладывания соответствующих длин отрезков на лучах, исходящих из начала координат под соответствующими углами относительно оси абсцисс, кратными выбранному угловому интервалу. Геометрические параметры поперечного сечения тела определяют расчетным путем, при этом длину контура определяют как сумму длин прямых линий между всеми соседними контрольными точками, площадь определяют как сумму всех элементарных площадей секторов, центральный угол которых равен выбранному угловому интервалу и радиусы каждого из которых равны среднему арифметическому значению длин двух отрезков между центральной и каждой из соседних контрольных точек, за максимальный размер принимают длину наибольшего отрезка из множества отрезков между всеми возможными парами контрольных точек, за минимальный - сумму максимального расстояния от этого наибольшего отрезка до контрольных точек, лежащих по одну сторону от него, и максимального расстояния от этого наибольшего отрезка до контрольных точек, лежащих по другую сторону от него.
Такое выполнение способа позволяет, проводя измерения только лишь из одной базовой точки, получить координаты всех контрольных точек, расположенных на контуре сечения тела (штамба саженца или укорененного черенка растения квазицилиндрической формы), по которым можно получить полную информацию о сечении тела: конфигурацию и длину контура, площадь, отношение максимального и минимального ортогональных размеров - индекс формы. Так, например, при достаточно большом количестве контрольных точек участок контура между соседними контрольными точками можно аппроксимировать прямой линией и длину этой линии вычислить по формулам аналитической геометрии, а длину контура, соответственно, как сумму длин между всеми соседними контрольными точками. А участок площади сечения, ограниченный частью контура между соседними контрольными точками и лучами, исходящими из центральной точки в эти контрольные точки, можно аппроксимировать сектором круга с радиусом равным среднему арифметическому значению отрезков лучей от центральной до контрольных точек. Поскольку углы между всеми отрезками лучей одинаковы и длины всех отрезков лучей известны, то площадь каждого сектора вычисляется как часть площади круга по известной формуле. Сектора отличаются друг от друга только радиусами. Для уменьшения методической погрешности радиусы вычисляются как среднее арифметическое значений двух соседних отрезков лучей от центральной до двух соответствующих контрольных точек. Количество секторов равно целому числу угловых интервалов в пределах одного оборота вращения контролируемого поперечного сечения, а площадь сечения - сумме площадей всех секторов. Другим вариантом может быть нахождение аппроксимирующих функций отдельных частей контура по координатам контрольных точек и дальнейшее вычисление длины контура и площади сечения с помощью интегрального исчисления. Конфигурация контура сечения тела может быть получена путем нанесения контрольных точек на координатную плоскость. Известные координаты контрольных точек позволяют вычислять расстояния между любыми точками. Следовательно, способ позволяет найти максимальный размер сечения. Из уравнения прямой, проходящей через контрольные точки, соответствующие максимальному размеру сечения, с помощью формул аналитической геометрии определяются максимальные размеры в ортогональном направлении в одну и другую стороны относительно этой прямой и, соответственно, коэффициент формы.
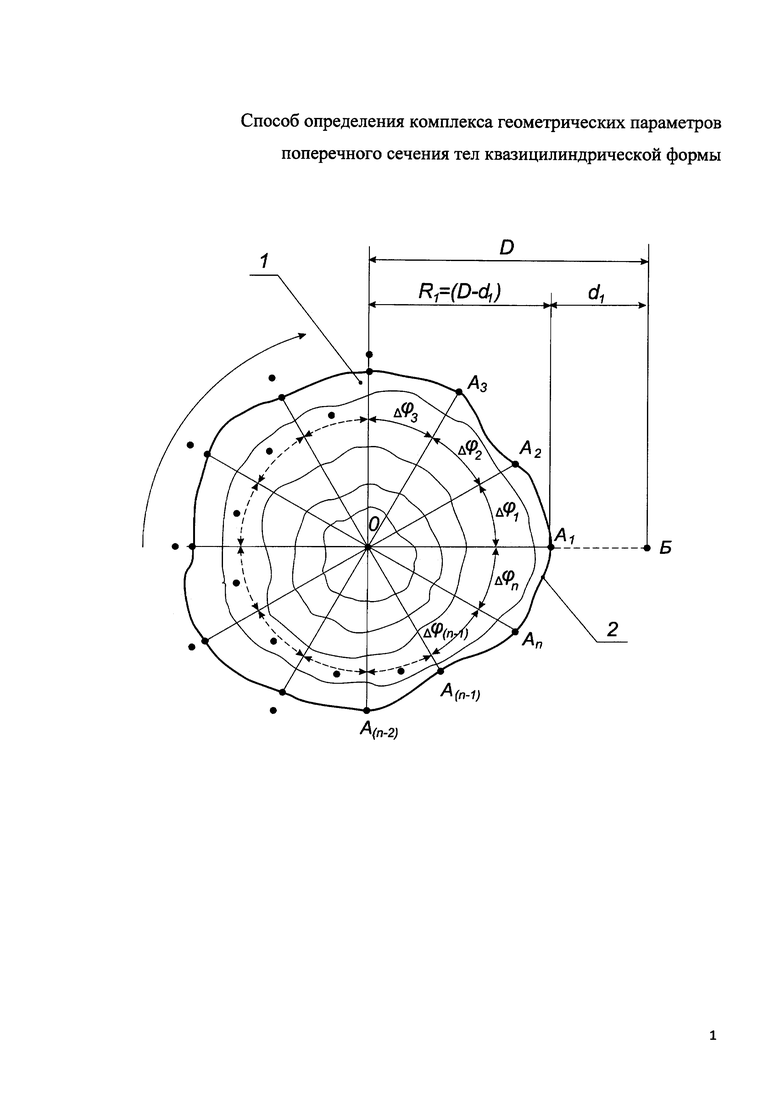
На фиг. изображен рисунок, поясняющий сущность способа определения комплекса геометрических параметров поперечного сечения тел квазицилиндрической формы.
Способ определения комплекса геометрических параметров поперечного сечения тел квазицилиндрической формы реализуется в последовательности действий, изложенной ниже.
В исходном состоянии, показанном на рисунке, поясняющем сущность способа, производят измерение расстояния d1 от базовой точки Б, расположенной на заданной (известной) дистанции D от центральной точки О, находящейся в пределах контролируемого сечения 1, до первой контрольной точки А1, расположенной на пересечении линии контура 2 сечения 1 с линией, соединяющей точки О и Б. Затем вычисляют длину отрезка R1 между точками О и А1, как разность дистанции D и расстояния d1. Далее поворачивают контролируемое сечение 1 вокруг точки О (центр вращения) на заданный (известный) угол Δϕ1, размер которого выбирают так, чтобы частное от деления числа 360 (угол при повороте на один оборот в градусах) Δϕ1 (в градусах) было целым числом n. При этом на линии, соединяющей точки О и Б, будет располагаться следующая контрольная точка, то есть А2, до которой производят аналогичное измерение расстояния d2, по результату которого аналогичным образом вычисляют длину отрезка R2. Таким образом, последовательно поворачивая контролируемое сечение 1 на углы равные Δϕ1, получают n значений длин отрезков R1…Rn. Далее эти значения длин отрезков R1…Rn и значение выбранного углового интервала Δϕ1 используют для определения координат всех контрольных точек в прямоугольной (декартовой) системе координат. Для этого за начало прямоугольной системы координат принимают центральную точку О. Затем первый вычисленный отрезок R1 между точками О и A1 откладывают от начала координат на оси абсцисс и координаты конца отрезка принимают за координаты первой контрольной точки A1. Для получения координат второй контрольной точки А2 из начала системы координат под углом Δϕ1 (в направлении против часовой стрелки) проводят луч, на котором откладывают второй вычисленный отрезок R2 и координаты его конца принимают за координаты второй контрольной точки А2. Далее из начала системы координат в пределах координатной плоскости проводят семейство лучей, каждый из которых отстоит от предыдущего на угол Δϕ1. На этих лучах последовательно откладывают вычисленные отрезки R3…Rn и получают координаты остальных контрольных точек А3…An. Абсциссы контрольных точек А1…An определяют путем умножения длины соответствующего отрезка R1…Rn на косинус угла между этим отрезком и осью абсцисс, а ординаты контрольных точек А1…An - умножением длины соответствующего отрезка R1…Rn на синус того же угла. Зная координаты всех контрольных точек А1…An, лежащих на контуре 2 поперечного сечения 1, методами аналитической геометрии определяют необходимые параметры поперечного сечения 1. Длину контура 2 определяют как сумму длин прямых линий между всеми соседними контрольными точками семейства А1…An. Длину каждой прямой линии между точками вычисляют с помощью теоремы Пифагора как гипотенузу прямоугольного треугольника, катетами которого являются проекции этой линии на оси абсцисс и ординат. Площадь сечения 1 определяют как сумму всех элементарных площадей секторов, центральный угол которых равен выбранному угловому интервалу Δϕ1 и радиусы каждого из которых равны среднему арифметическому значению длин двух соседних отрезков из семейства R1…Rn. Площадь каждого сектора вычисляют путем деления площади круга с соответствующим радиусом на количество секторов n. За максимальный размер принимают длину наибольшего отрезка из множества отрезков между всеми возможными парами контрольных точек семейства А1…An, за минимальный - сумму максимального расстояния от этого наибольшего отрезка до контрольных точек из множества А1…An, лежащих по одну сторону от него, и максимального расстояния от этого наибольшего отрезка до контрольных точек из множества А1…An, лежащих по другую сторону от него.
Размер углового интервала Δϕ1 выбирают исходя из допускаемой методической погрешности определения геометрических параметров поперечного сечения, возникающей из-за аппроксимации реальной конфигурации контура и площади поперечного сечения набором прямых линий и секторов, соответственно.
Так, например, для поперечного сечения, имеющего форму эллипса с размерами большой и малой полуосей 50 и 10 и площадью 1571 условных единиц, соответственно, результаты расчета методической погрешности определения площади в зависимости от размера углового интервала Δϕ приведены в таблице.
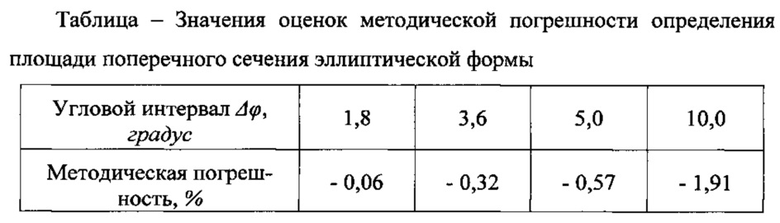
Из таблицы следует, что для большинства практических применений способа дискретность угла поворота объекта исследований можно выбирать в пределах от 3,6 до 10,0 градусов. Так, при дискретности угла поворота сечения 3,6 градуса количество контрольных точек будет равно 100. Тогда, например, при поперечном размере сечения 15 мм, длине контура около 45 мм расстояние между точками будет около 0,45 мм, и при размерах светового пятна лазера 0,1 мм контрольные точки не будут сливаться.
Процесс выполнения описанных действий может быть осуществлен с помощью следующих материальных средств.
Измерения расстояний d1…dn от базовой точки Б до контрольных точек А1…An осуществляют с помощью лазерных триангуляционных датчиков LS5 НПП «ПРИЗМА», имеющих размер светового пятна на объекте около 0,1 мм, что позволяет детализировать форму контура сечения с высокой точностью [URL:http://www.prizmasensors.ru]. Дистанцию D (расстояние датчика LS5 до центральной точки О) обеспечивают конструктивно. Последовательные повороты квазицилиндрического объекта (саженца) и его контролируемого сечения 1 вокруг точки О (центра вращения) на заданные (известные) угловые интервалы Δϕ1 осуществляют посредством шагового двигателя PL42H34-D5 и драйвера PLD230 [URL:http://www.purelogic.ru], управляющего двигателем и запуском измерений датчика расстояний LS5 после остановки шагового двигателя в заданном угловом положении. При этом ось вращения двигателя проходит через центральную точку О и между захватными губками, удерживающими квазицилиндрический объект (саженец) в вертикальном положении. Повороты квазицилиндрического объекта (саженца) можно осуществлять также и без остановок через каждые заданные угловые интервалы Δϕ1, например, двигателем с редуктором РД-09 [URL:http://www.kipspb.ru]. Для запуска измерений расстояний d1…dn в этом случае используют датчик углового положения, например, инкрементальный угловой фотоэлектрический преобразователь перемещений ЛИР [URL:http://www.skbis.ru]. Все необходимые вычисления длин отрезков R1…Rn, координат контрольных точек A1…An и комплекса геометрических параметров поперечного сечения тел квазицилиндрической формы производят с помощью микроконтроллера, получающего информацию в виде электрических сигналов от лазерного триангуляционного датчика LS5, драйвера PLD230 или инкрементального датчика углового положения ЛИР, и соответствующего программного обеспечения. В качестве микроконтроллера используют, например, микросхему PIC16F876 [URL:http://www.rudatasheet.ru].
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ КОМПЛЕКСА ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ПОПЕРЕЧНОГО СЕЧЕНИЯ ТЕЛ КВАЗИЦИЛИНДРИЧЕСКОЙ ФОРМЫ | 2016 |
|
RU2642481C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ СЕЧЕНИЯ ТЕЛА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2013 |
|
RU2551264C2 |
| СПОСОБ И УСТРОЙСТВО КОНТРОЛЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ДВИЖУЩИХСЯ ЖЕЛЕЗНОДОРОЖНЫХ РЕЛЬСОВ | 2024 |
|
RU2837941C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ИЗДЕЛИЙ И ЦЕЛЕВОЙ ЗНАК ДЛЯ ОПРЕДЕЛЕНИЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ИЗДЕЛИЙ | 2000 |
|
RU2202101C2 |
| СПОСОБ ИЗМЕРЕНИЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ СТАЛЬНОГО ЛИСТА, ДВИЖУЩЕГОСЯ ПО РОЛЬГАНГУ, И ЛАЗЕРНАЯ ИЗМЕРИТЕЛЬНАЯ СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2016 |
|
RU2621490C1 |
| СПОСОБ БЕСКОНТАКТНОГО ИЗМЕРЕНИЯ ТОПОГРАФИИ ПОВЕРХНОСТИ ОБЪЕКТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2001 |
|
RU2208370C2 |
| СПОСОБ КОНТРОЛЯ ПРОФИЛЯ ИЗДЕЛИЯ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2003 |
|
RU2263879C2 |
| УСТРОЙСТВО ДЛЯ КОНТРОЛЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ЦИЛИНДРИЧЕСКИХ ИЗДЕЛИЙ С РЕЗЬБОВОЙ ПОВЕРХНОСТЬЮ | 2008 |
|
RU2386925C2 |
| БЕСКОНТАКТНОЕ УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ РАССТОЯНИЯ ДО РАЗЛИЧНЫХ ТОЧЕК ПОВЕРХНОСТИ ОБЪЕКТА | 2008 |
|
RU2383858C2 |
| Способ оптического контроля качества и определения размера плодоовощной продукции шарообразной формы при сортировке на конвейере | 2024 |
|
RU2837834C1 |
Изобретение относится к области контрольно-измерительной техники и может использоваться для определения комплекса геометрических параметров поперечного сечения тел квазицилиндрической формы. Способ определения геометрических параметров сечения тела заключается в том, что измеряют расстояния от базовой точки, расположенной на фиксированной дистанции от центральной точки, находящейся в пределах контролируемого поперечного сечения тела, до соответствующих контрольных точек на контуре сечения тела по направлению к этой центральной точке при вращении контролируемого поперечного сечения тела вокруг оси, проходящей через центральную точку перпендикулярно плоскости сечения, начиная от начального углового положения через каждые одинаковые угловые интервалы в пределах одного оборота, и определяют длины отрезков между центральной и контрольными точками путем вычитания измеренных расстояний из расстояния между базовой и центральной точками. Затем определяют координаты всех полученных контрольных точек и геометрические параметры поперечного сечения тела: длину контура, площадь, максимальный и минимальный ортогональные размеры и их отношение - индекс формы. Технический результат - снижение трудоемкости определения комплекса геометрических параметров поперечного сечения тела. 2 з.п. ф-лы, 1 ил., 1 табл.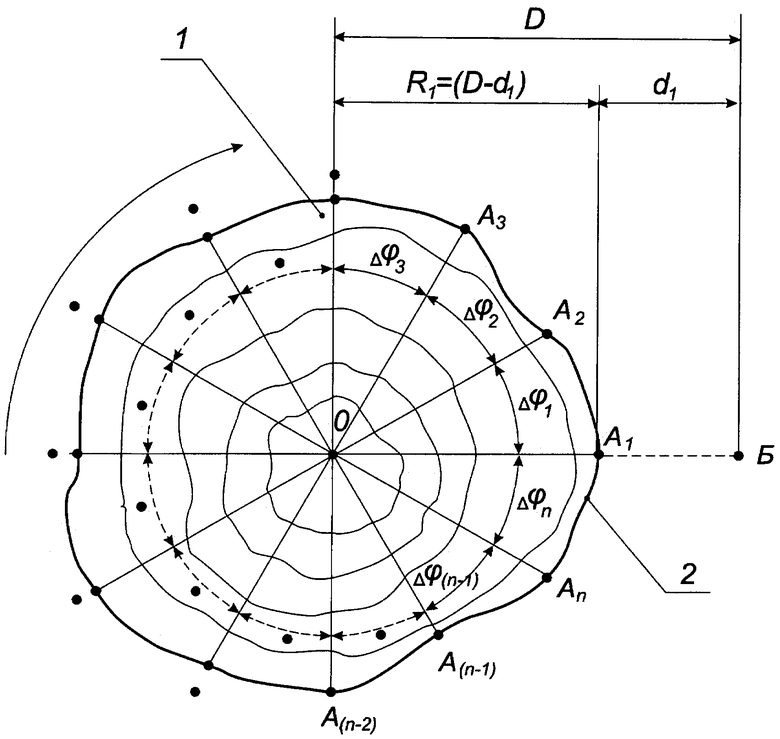
1. Способ определения комплекса геометрических параметров поперечного сечения тел квазицилиндрической формы, включающий измерения расстояний от базовой точки, расположенной в плоскости контролируемого поперечного сечения на определенном расстоянии от поверхности тела, до соответствующих контрольных точек, расположенных на контуре поперечного сечения тела, отличающийся тем, что базовую точку располагают на фиксированной дистанции от центральной точки, находящейся в пределах контролируемого поперечного сечения тела, и осуществляют измерения расстояний от базовой точки до контрольных точек по направлению к этой центральной точке при вращении контролируемого поперечного сечения тела вокруг оси, проходящей через центральную точку перпендикулярно плоскости сечения, начиная от начального углового положения через каждые одинаковые угловые интервалы в пределах одного оборота, затем определяют длины отрезков между центральной и контрольными точками, как разности между фиксированной дистанцией базовой точки от центральной точки и измеренными расстояниями от базовой точки до каждой из контрольных точек, и по полученным значениям длин отрезков и выбранному значению угловых интервалов определяют координаты всех контрольных точек в прямоугольной системе координат и геометрические параметры сечения тела: длину контура, площадь, максимальный и минимальный ортогональные размеры и их отношение - индекс формы, при этом значение угловых интервалов выбирают так, чтобы их число в пределах оборота было целым.
2. Способ по п. 1, отличающийся тем, что для определения координат контрольных точек центральную точку принимают за начало прямоугольной системы координат, длину отрезка между центральной и контрольной точкой, определенную при начальном угловом положении контролируемого поперечного сечения, откладывают от начала системы координат на оси абсцисс и координаты конца отрезка принимают за координаты первой контрольной точки, координаты остальных контрольных точек получают аналогично путем откладывания соответствующих длин отрезков на лучах, исходящих из начала координат под соответствующими углами относительно оси абсцисс, кратными выбранному угловому интервалу.
3. Способ по п. 1, отличающийся тем, что геометрические параметры поперечного сечения тела определяют расчетным путем, при этом длину контура определяют как сумму длин прямых линий между всеми соседними контрольными точками, площадь определяют как сумму всех элементарных площадей секторов, центральный угол которых равен выбранному угловому интервалу и радиусы каждого из которых равны среднему арифметическому значению длин двух отрезков между центральной и каждой из соседних контрольных точек, за максимальный размер принимают длину наибольшего отрезка из множества отрезков между всеми возможными парами контрольных точек, за минимальный - сумму максимального расстояния от этого наибольшего отрезка до контрольных точек, лежащих по одну сторону от него, и максимального расстояния от этого наибольшего отрезка до контрольных точек, лежащих по другую сторону от него.
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ СЕЧЕНИЯ ТЕЛА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2013 |
|
RU2551264C2 |
| Способ контроля формы профиля прозрачных осесимметричных тонкостенных оболочек | 1991 |
|
SU1776988A1 |
| US 3982816 A1, 28.09.1976 | |||
| СПОСОБ ИЗМЕРЕНИЯ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ОБОЛОЧКИ ВРАЩЕНИЯ | 2010 |
|
RU2426067C1 |
| US 7920278 B2, 05.04.2011. | |||
Авторы
Даты
2018-02-15—Публикация
2016-07-12—Подача