СПОСОБ КОНТРОЛЯ СДВИГОВЫХ ДЕФОРМАЦИЙ Российский патент 1994 года по МПК G01N3/24 G01B5/00 

Изобретение относится к техническим измерениям, а именно к контролю геометрических параметров витых и невитых слоистых объектов, например стальных канатов, тросов, поликристаллических изделий и других различных материалов, и может быть использовано в любой отрасли народного хозяйства, связанных с их производством, испытанием и исследованием.

Известен способ контроля упругой отдачи шага свивки в отрезанном образце от витого объекта, заключающийся в определении разницы между длинами вырезанного и невырезанного образца исследуемого объекта.

Также известен способ контроля равнонапряженности отдельных слоев или элементов в многослойных витых объектах, согласно которому замеряют величину упругой отдачи каждого слоя или отдельного элемента и по величинам упругой отдачи судят о напряженности отдельных слоев и элементов.

Известен, например, способ определения остаточных напряжений по изменению размеров колец или полосок, вырезанных из различных поликристаллических материалов.

Известен способ контроля разрывного усилия каната или поликристаллического образца, включающий отбор образца, его растяжение до разрушения и определение максимального разрывного усилия в момент образования шейки на деформируемом образце.

Целью изобретения является повышение качества контроля путем учета взаимодействия и равнонапряженности слоев.

Эффективность предлагаемого способа заключается в том, что он позволяет вносить коррективы в технологию производства канатов и поликристаллов, повышать их фактическую прочность и увеличивать срок их службы и качество за счет обеспечения равнонапряженности всем структурным элементам.

Для реализации способа использована формула:
i= ( Δ)/Д , (1) где i - коэффициент равнонапряженности элементов материала;
Δ - величина сдвига каждого элемента;
Д - диаметр (высота) материала;
1, 2, 3. . . n - номера элементов материала.

Из гипотезы плоских сечений вытекает, что плоские сечения, проведенные в теле по деформации, остаются плоскими и после деформации.

Поэтому предполагалось, что при растяжении бруса или каната продольные волокна испытывают одинаковые удлинения и напряжения по всему сечению.

Для такого материала расчетная формула для определения напряжений по сечениям, перпендикулярным к оси стержня, исходила из уравнения равновесия:
-P+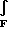 σ×dF= 0. (2)
Однако из исследования ненагруженных стальных канатов стало известно, что по сечению серийных канатов структурны элементы находятся с неоднородными микронапряжениями сжатия или растяжения и имеют различную длину, которая и является причиной межструктурного сдвига, вызванного различной величиной перемещений торцовых поверхностей элементов под действием неоднородных усилий сжатия или растяжения при нарушении связей между элементами в процессе разрезания каната.

Поэтому, если серийный канат подвергнуть растяжению до разрушения, то канат разрушится не одновременно всеми элементами, а разрушение будет протекать ступенчато: вначале разрушится короткий элемент, что будет соответствовать максимальной прочности каната в момент образования ступенчатой шейки, затем прочность каната будет падать по мере разрушения более длинных элементов и окончательное разрушение каната произойдет при минимальной прочности в момент разрушения наиболее длинного элемента.

Так же известно, что и при растяжении поликристаллических образцов, максимальная прочность всегда обеспечивается в момент образования шейки, затем прочность образца падает, при этом известные рентгенографические исследования показывают, что наружные слои образца деформируются пластически при меньших напряжениях, чем остальной объем образца.

Тогда с учетом перемещений торцовых поверхностей всех структурных элементов на одинаковую величину в любом равнонапряженном объекте, например, в поликристалле или канате, выполненных по принципу равенства длин всех структурных элементов, известное выражение равновесия 2 примет вид:
-P± S+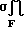dF± 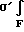dF= 0. (3)
После интегрирования и простейшего преобразования выражение 3 примет окончательный вид:
σ′′= σ±σ′. (4)
Но в выражении ( 4 ) каждому напряжению будет соответствовать и своя упругая деформация, а именно
Δ1^′′= Δ1= Δ1^′ , (5) где Р - усилие растяжения материала;
S - усилие сжатия или растяжения стуктурных элементов по сечению материала;
F - площадь поперечного сечения;
σ- макронапряжение материала с недеформированными структурными элементами;
σ′ - микронапряжение сжатия (знак плюс) или растяжения (знак минус) структурных элементов по сечению материала;
σ′′ - общее напряжение материала;
Δ1^′′ - общая упругая деформация материала;
Δ1 - упругая деформация материала с недеформированными структурными элементами;
Δ1^' - упругая деформация от микронапряжений сжатия или растяжения.

Из анализа выражений (4) и (5) вытекает, что в любом равнонапряженном объекте, выполненным по принципу равенства длин всех однородных структурных элементов, совместность упругих деформаций и напряжений в любой момент его нагружения будет обеспечена только в том случае, если все структурный элементы в нем будут находиться с одинаковой алгебраической суммой или разностью упругих деформаций от макро- и микронапряжений и одинаковой алгебраической суммой или разностью макро- и микронапряжений, а именно
Δl′′= Δl± Δl′= const , (6)
σ′′= σ± σ′= Const. (7)
Поэтому, только в любом равнонапряженном объекте плоские сечения, проведенные до деформации, будут оставаться плоскими при деформации и после разрушения в связи с одновременным разрушением всех элементов одинаковой длины по одной нормальной плоскости.

Реальныe канаты и поликристаллы из-за наличия в них сдвига между структурными элементами, вызванного неоднородными микронапряжениями сжатия или растяжения, разрушаются не одновременно всеми структурными элементами, а разрушение всегда начинается с короткого и заканчивается самым длинным элементом.

Ступенчатое разрушение элементов является причиной снижения фактической прочности материала и образования шеек на разрушенных образцах.

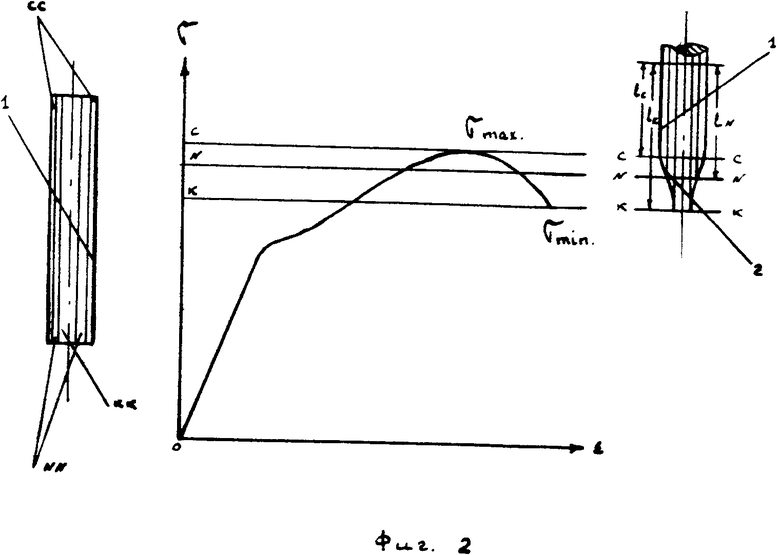
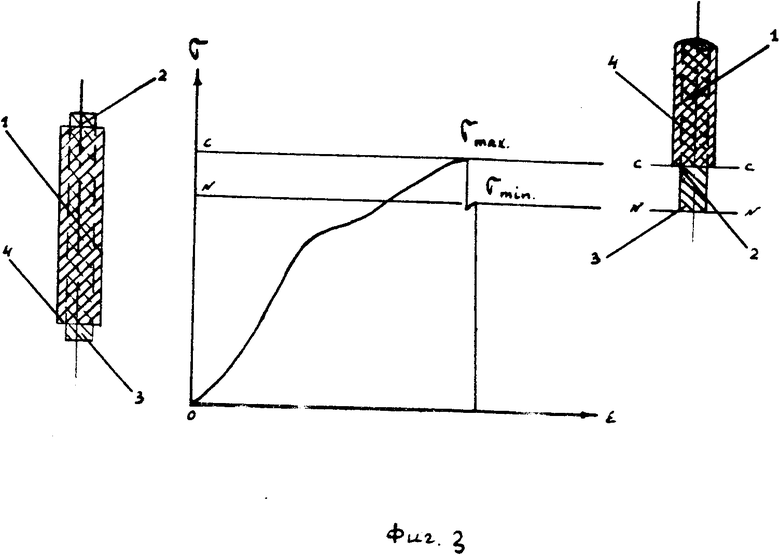
На фиг. 1а, г изображены неразрушенные образцы равнонапряженного трехслойного каната и поликристалла 1; на фиг. 1б, д - те же образцы после одновременного разрушения всех элементов по нормальной плоскости 5; на фиг. 2 и 3 - слева изображены неразрушенные образцы реального поликристалла и двухслойного каната 1, а справа - диаграммы их растяжения и половинки разрушенных образцов с наличием шеек, расположенных на участках диаграммы, соответствующих их образованию.

На фиг. 1а в вырезанном ненагруженном канатном образце 1 поверхностный, промежуточный и центральный слои 2, 3, 4 имеют одинаковую длину, а торцовые поверхности указанных слоев совмещены с нормальными плоскостями 5 образца 1.

Из-за разрушения канатного образца 1 одновременно всеми концентрическими слоями 2, 3, 4 по нормальной плоскости разрушения 5 в разрушенном образце 1, если его половинки соединить и замерить фактические длины концентрических слоев 2, 3, 4, то длины всех слоев также будут одинаковыми, но размеры их окажутся длиннее аналогичных слоев 2, 3, 4 в ненагруженном образце 1 на величину одинаковой пластической деформации каждого слоя.

Поэтому одинаковой длине концентрических слоев 2, 3, 4 в ненагруженном образце 1 будут соответствовать одинаковые длины концентрических слоев 2, 3, 4 в разрушенном образце 1, т. е. длины элементов в ненагруженном и разрушенном образце являются адекватными.

Например, если бы в ненагруженном образце 1 поверхностный концентрический слой 2 по длине был короче концентрических слов 3, 4, то с короткой длиной поверхностный слой 2 находился бы и в разрушенном образце 1, и наоборот, если бы поверхностный концентрический слой 2 в ненагруженном образце 1 находился с наибольше длиной, то с аналогичной длиной он бы находился и в разрушенном образце.

Если теперь по высоте ненагруженных образцов 1, вырезанных из равнонапряженного каната или поликристалла (фиг. 1а, г), в любом месте провести одну или несколько плоскостей СС, параллельных нормальным торцовым плоскостям 5 вырезанных образцов 1, то указанные плоскости будут оставаться параллельными как при нагружении образцов 1, так и после их разрушения в связи с одинаковыми удлинениями и напряжениями по всему сечению как в ненагруженных, так и деформированных образцах 1.

Тогда по аналогии с адекватностью длин в ненагруженном и разрушенном образцах 1 равнонапряженного каната, одинаковые длины будут иметь и все слои, например поверхностный 2 и центральный слой 3 в ненагруженном и разрушенном образцах 1 равнонапряженного поликристалла (фиг. 1г, д).

Одновременное разрушение всех элементов одинаковой длины по нормальной плоскости 5 свидетельствует об отсутствии сдвиговых деформаций между элементами в любом равнонапряженном объекте.

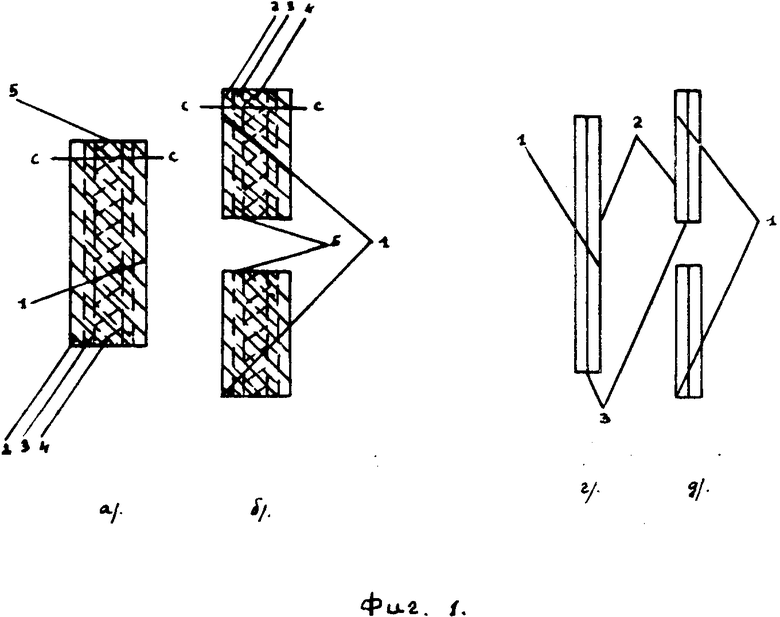
На фиг. 3 слева изображен образец 1, вырезанный из двухслойного серийного каната, выполненного из центрального и поверхностного концентрических слоев 3 и 4.

В связи с тем, что концентрически слои 3 и 4 по сечению ненагруженного каната находились с неоднородными микронапряжениями сжатия, при вырезке образца 1, из-за нарушения связей между элементами, торцовые поверхности указанных слоев переместились на неодинаковую величину в осевом направлении и провели к образованию ступенчатой шейки 2 в вырезанном образце 1, которая оказалась следствием сдвига торцовой поверхности концентрического слоя 3 относительно торцовой поверхности поверхностного концентрического слоя 4, что и привело к изменению длин концентрических слоев 3 и 4.

При этом с наибольшей длиной оказался наиболее сжатый центральный слой 3, а с наименьшей длиной - менее сжатый поверхностный слой 4.

Если теперь вырезанный образец 1 подвергнуть растяжению до разрушения, то и в разрушенном образце 1 (фиг. 3, справа) образуется также ступенчатая шейка 2, аналогичная ступенчатой шейке 2, которая образовалась на ненагруженном образце 1 в процессе его вырезки из исследуемого серийного каната.

В разрушенном образце 1 наименьшую пластическую деформацию будет иметь короткий, менее сжатый поверхностный слой 4, с наибольшей пластической деформацией и длиной будет находиться более сжатый центральный слой 3.

Тогда разница между длинами концентрических слоев 3 и 4 в ступенчатой шейке 2 разрушенного образца 1 и будет представлять собой величину сдвиговой деформации торцовой поверхности NN концентрического слоя 3 относительно торцовой поверхности СС концентрического слоя 4.

При этом на диаграмме растяжения образца 1 максимальная прочность ( σ_макс) будет соответствовать моменту образования на образце ступенчатой шейки или началу разрушения короткого поверхностного слоя 4 по сечению СС, затем произойдет мгновенный сброс нагрузки на участке диаграммы CN, связанный с выбиранием слабины на центральном слое 3 и после его натяжения, произойдет разрушение и центрального слоя 3 по сечению NN, но уже при минимальной прочности (σ_мин), что и повлечет за собой снижение фактической прочности разрушенного образца 1 из-за неодновременного разрушения обоих концентрических слоев 3 и 4 различной длины в серийном канате.

Таким образом различная пластическая деформация или различная длина концентрических слоев 3 и 4 в разрушенном образце 1 является свидетелем неоднородного упругонапряженного состояния указанных слов в ненагруженном образце 1.

В частности, если поверхностный слой 4 с короткой длиной, а центральный слой 3 с наибольшей длиной будут находиться в разрушенном образце 1, то указанные слои с аналогичными длинами будут находиться также и в ненагруженном образце 1, но по объему ненагруженного каната длины указанных слоев будут выравнены взаимно уравновешенными неоднородными микронапряжениями сжатия, при этом более длинный слой 3 в канате будет сжат больше, чем короткий поверхностный слой 4.

С неоднородными микронапряжениями сжатия или растяжения или различными длинами также находятся и различные части в ненагруженных поликристаллах, о чем свидетельствует различная пластическая деформация или их различная длина по высоте общеизвестной шейки в виде эллиптического или гиперболического параболоидов, которая также является следствие ступенчатого и последовательного разрушения концентрических слоев неодинаковой длины, которая непрерывно увеличивается от поверхности к центру или наоборот от центра к поверхности в ненагруженных образцах деформированных поликристаллов.

На фиг. 2 слева изображен неразрушенный круглый образец из мягкой стали, а справа диаграммы напряжений - тот же, но разрушенный образец 1 с общеизвестной шейкой 2 в виде эллиптического параболоида, формированию которого на диаграмме растяжения соответствует участок ( σ_макс-σ_мин).

При этом максимальная прочность при растяжении образца 1 будет соответствовать моменту образования на образце шейки или началу разрушения короткого поверхностного слоя l_с по сечению СС, затем произойдет последовательное разрушение более длинных слоев и окончательное разрушение образца 1 завершится разрушением длинного центрального слоя l_к по сечению КК, но уже при минимальной прочности, что и повлечет за собой снижение фактической прочности разрушенного образца из-за неодновременного разрушения всех концентрических слоев различной длины в реальном поликристалле.

С целью упрощения рассуждения, в разрушенном образце 1, по высоте шейки 2, рассмотрим три самостоятельных концентрических слоя: поверхностный СС, промежуточный NN и центральный КК длины которых оказались равными:
l_c< l_N< l_к.
А это означает, что с указанными адекватными длинами поверхностный, промежуточный и центральный слои находятся и в ненагруженном образце 1 реального поликристалла, но по его объему выравнены взаимно уравновешенными неоднородными микронапряжениями сжатия.

При этом поверхностный слой СС как наименее сжатый элемент в ненагруженном поликристалле 1 имеет короткую длину, а средний слой NN, как более сжатый элемент, имеет промежуточную длину, и центральный слой КК как наиболее сжатый элемент имеет наибольшую длину, так как неоднородные микронапряжения сжатия указанных слоев будут равны: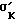
< < .

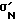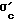Об этом также свидетельствует и различная пластическая или сдвиговая деформация указанных слоев по высоте шейки 2 разрушенного образца 1 относительно первоначальной длины l невырезанного образца 1, а именно
Δ l_c = l_c - l (8)
Δ l_N = l_N - l (9)
Δ l_к = l_к - l (10)
Тогда из выражений 8, 9, 10 вытекает, что:
Δl_к>Δl_N>Δl_с . (11)
А это означает, что рассматриваемые слои по объему ненагруженного образца 1 реального поликристалла находятся в различном упругонапряженном состоянии и различными упругими деформациями от микронапряжений сжатия, а именно
Δl′к

>Δl′N >Δl′с . (12)
Параболообразная кривая и прямая линия на участках диаграмм растяжения ( σ_макс-σ_мин), соответствующих формированию шеек на деформируемых образцах реального поликристалла и каната, обусловлены различием в жесткости связей между смежными слоями.

Если в канате связь между смежными слоями в основном осуществляется силами трения, то в поликристалле силы трения многократно усиливаются межатомными силами взаимодействия, в связи с чем в поликристалле смежные слои находятся с более плотной упаковкой, чем в канате.

Поэтому непрерывное разрушение сдвинутых слоев относительно друг друга в поликристалле осуществляется по плавной кривой, а в канате - по прямой линии в связи со скачкообразным разрушением смежных слоев также различной длины.

Связи между смежными слоями в поликристалле могут быть устранены путем последовательного стравливания поверхностных слоев, при этом после каждого поверхностного стравливания длина исследуемого образца будет непрерывно возрастать.

Тогда замеренная разница между длиной образца после стравливания поверхностного слоя и первоначальной длиной образца до стравливания, принятой за базовый элемент, и определит сдвиговую деформацию любого слоя в поликристалле.

В канате связи между одиночными элементами или слоями устраняют разливкой элементов, находят короткий элемент и принимают его за базовую длину.

Тогда замеренная разница между длинами искомого и базового элемента определит сдвиговую деформацию любого длинного элемента в любом серийном канате.

Зная суммарную величину сдвиговых деформаций всех элементов или слоев, по формуле 1, судят о степени равнонапряженности структурных элементов в любом канате или поликристаллическом материале, при этом при коэффициенте равнонапряженности, равным нулю, материалы или изделия относят к высокому уровню качества изготовления, так как только в идеальных равнонапряженных материалах и изделиях, выполненных по принципу равенства длин всех элементов, сдвиг между элементами будет отсутствовать, что и приведет к их равномерному нагружению в процессе эксплуатации и повышению агрегатной прочности материалов за счет одновременного разрушения всех элементов по нормальной плоскости.

Способ контроля сдвиговых деформаций осуществляется следующим образом.

Учитывая, что в любом равнонапряженном объекте, например канате или поликристалле, сдвиговые деформации между слоями или отдельными элементами всегда отсутствуют, а все элементы одновременно разрушаются по одной нормальной плоскости, коэффициент равнонапряженности для равнонапряженного объекта, согласно выражения 1, будет равен нулю, а именно:
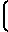
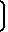i₁= 0/Д= 0.

На фиг. 3 изображен двухслойный канат конструкции 18 х 19 + 1 о. с. диаметром 10 мм. Предположим, что после агрегатного разрушения каната величина сдвига между торцовыми поверхностями концентрических слоев 3 и 4 составила:
CN = 8 мм.

Тогда коэффициент равнонапряженности для такого каната будет равен:
i₂ = 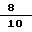= 0,8.

Теперь замер сдвиговых деформаций произведем по выплетенным элементам, например, из трехпрядного каната конструкции 3 х 27 ГОСТ 3093-80 диаметром 17,0 мм.

Предположим, что длины выплетенных прядей оказались равными: 1000, 1005, 1008 мм.

За базовый элемент принимаем короткую длину 1000 мм.

Сдвиговые деформации для двух более длинных прядей будут равны: 5 и 8 мм.

Коэффициент равнонапряженности каната будет равен:
i₃ = 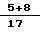= 0,76.

Замер сдвиговых деформаций по круглому образцу диаметром 6,0 мм с базовой длиной 200 мм из стали марки 0 произведем с участием фиг. 2 на которой ненагруженный образец 1 изображен слева.

После разрушения образца 1 обе его половинки соединяют и профиль образца переносят на лист бумаги путем обводки образца по всему контуру (на фиг. 2 изображена одна половинка образца).

Затем через границу начала образования шейки проводят плоскость СС, перпендикулярную оси образца и параллельно указанной плоскости, например через каждый миллиметр по длине (высоте) шейки проводят другие плоскости, например, NN, КК и т. д. , при этом каждая плоскость будет соответствовать тому или иному слою в разрушенном образце.

После этого замеряют длину каждого слоя и по разнице между замеренной длиной искомого слоя и первоначальной базовой длиной образца, равной 200 мм, определяют сдвиговую деформацию для каждого слоя и по суммарной величине замеренных сдвиговых деформаций всех слоев по формуле 1 судят о равнонапряженности слоев в исследуемом поликристалле.

Например, согласно выражений 8, 9, 10 сдвиговые деформации поверхностного СС, промежуточного NN и центрального слоя КК, изображенных на фиг. 2 оказались равными 1, 3 и 5 мм.

Тогда с учетом замеренных сдвиговых деформаций для трех выделенных слоев коэффициент равнонапряженности будет равен:
i₄ = 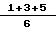= 1,5.

По аналогии с рассмотренным примером производят замер сдвиговых деформаций самостоятельных слоев в поликристалле после устранения связей между слоями путем непрерывного стравливания поверхностных слоев, при этом за базовую длину принимают длину образца до его стравливания
Из анализа полученных коэффициентов равнонапряженности вытекает, что все рассмотренные объекты, за исключением равнонапряженного каната и поликристалла, далеки от совершенства и не удовлетворяют высокому уровню качества, так как их коэффициенты равнонапряженности значительно отличаются от нуля, что связано с наличием больших сдвиговых деформаций между слоями в рассмотренных реальных объектах. (56) Гурьянов Ю. А. Влияние межструктурного сдвига на прочность стальных канатов. - Сталь, N 10, 1990. с. 76-79.

Изобретение относится к испытательной технике и может быть использовано для контроля сдвиговых деформаций свитых канатов. Цель изобретения - повышение качества контроля канатов из прядей поликристаллических материалов. Из каната вырезают образец и подвергают образец полной развивке. Измеряют длину каждой пряди после развивки, выделяют самую короткую прядь и для нее осуществляют контроль сдвиговой деформации. 2 з. п. ф-лы, 3 ил.

1. СПОСОБ КОНТРОЛЯ СДВИГОВЫХ ДЕФОРМАЦИЙ в слоистых материалах, по которому на образец или изделие из слоистого материала воздействуют усилиями, измеряют и сопоставляют между собой деформации слоев, отличающийся тем, что, с целью повышения качества контроля путем учета взаимоействия и разнонапряженности слоев, измерение деформаций осуществляют после устранения связей между слоями, при измерении деформаций слои соединяют, замеряют длину каждого слоя находят короткий элемент и по разнице в длинах между короткими и более длинными элементами судят о сдвиговой деформации каждого элемента или суммарной сдвиговой деформации всех элементов по сечению образца. 2. Способ по п. 1, отличающийся тем, что для поликристаллических слоистых материалов связи между слоями устраняют стравливанием слоев. 3. Способ по п. 1, отличающийся тем, что для слоистых материалов, свитых из прядей, связи между слоями устраняют развивкой прядей.