Изобретение относится к радиоэлектронике и автоматике, предназначено для получения изменяющейся во времени по известному закону задержки сигнала и может быть использовано для обработки сигналов в реальном масштабе времени и для аналогового моделирования на основе штатных блоков АВМ.
Наиболее близок к предлагаемому способ переменной задержки τ (t) сигнала х(t), заключающийся в том, что сигнал пропускают через замкнутую систему с интеграторами, описываемую обыкновенным линейным дифференциальным уравнением с переменными коэффициентами. При этом параметры системы, определяющие величину задержки сигнала, изменяют ступенчато по закону τ*(t), аппроксимирующему непрерывный в общем случае закон τ (t). В течение k-го интервала τ*(t)= τк= const. Таким образом, здесь точность реализации закона изменения задержки τ(t) невысока.
Цель изобретения - повышение точности.
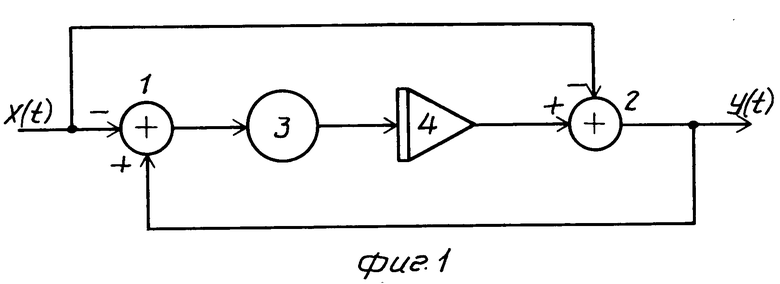
На фиг. 1 и 2 показаны структурные схемы устройств переменной задержки первого и второго порядков соответственно, реализующих предлагаемый способ.
Устройство задержки на интеграторах описывается дифференциальным уравнением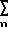 (θn/n!)yn = x (1) или дифференциальным уравнением
(θn/n!)yn = x (1) или дифференциальным уравнением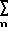 [(θ/2)n/n!]yn =
[(θ/2)n/n!]yn = 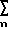 [(-θ/2)n/n!]xn , (2) где x(n) и y(n) - производные n-го порядка от входного x(t) и выходного y(t) сигналов; θ=θ (t) - закон изменения коэффициентов уравнений. Естественно, что в реальном устройстве на интеграторах количество слагаемых в суммах конечное. Для объяснения предлагаемого способа рассмотрим идеальные устройства, описываемые уравнениями (1) и (2), с бесконечным числом слагаемых (n изменяется от 0 до ∞). При этом суммы представляют собой ряды Тейлора (2), и равенства (1), (2) могут быть переписаны в виде
[(-θ/2)n/n!]xn , (2) где x(n) и y(n) - производные n-го порядка от входного x(t) и выходного y(t) сигналов; θ=θ (t) - закон изменения коэффициентов уравнений. Естественно, что в реальном устройстве на интеграторах количество слагаемых в суммах конечное. Для объяснения предлагаемого способа рассмотрим идеальные устройства, описываемые уравнениями (1) и (2), с бесконечным числом слагаемых (n изменяется от 0 до ∞). При этом суммы представляют собой ряды Тейлора (2), и равенства (1), (2) могут быть переписаны в виде
y[t + θ (t)] = x(t); (3)
y[t + θ (t)/2] = x [t - θ (t)/2] (4)
Равенство (3) не нарушается при одинаковом сдвиге по времени левой и правой частей на τ (t). При этом
y{t - τ (t) + θ [t- τ (t)]} = x [t - τ (t)]. (5)
Выполнение равенства
θ [t- τ (t)] = τ (t) (6) ведет к тому, что выражение (5) принимает вид
y(t) = x[t - τ (t)] (7)
Путем временного сдвига левой и правой частей равенства (4) на τ (t)/2 аналогично доказывается, что при выполнении условия (6) равенство (4) также принимает вид (7). Сдвигая левую и правую части равенства (6) на + 0(t) по времени, получают равносильное ему равенство
θ (t) = τ [t+ θ (t)]. (8)
Итак, доказано следующее. Если параметры системы с интеграторами θ (t) изменять по закону (6) или (8), то выходной сигнал y(t) запаздывает по отношению к входному сигналу х(t) на время τ (t) (согласно выражению (7)).
Примеры, иллюстрирующие связь между законами θ (t) и τ (t).
П р и м е р 1. Пусть требуется осуществить задержку τ (t)= α t + T,α = const, T= const. В этом случае уравнение (8) принимает вид θ (t)= α [t+ θ (t)] + T, откуда следует, что
θ (t) = (α t+ T)/(1- α).
В случае α = 0 (постоянная задержка) θ (t)= τ (t) = T. Чем ближе α к единице, тем больше θ (t) отличается от τ (t). Случай α = 1 при данном способе неосуществим, так как θ=∞ , случай α > 1 также неосуществим из-за неустойчивости дифференциальных уравнений (1) и (2).
П р и м е р 2. Пусть требуется осуществить задержку τ(t) = 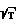 t ,, T= const. Тогда согласно выражению (8)
t ,, T= const. Тогда согласно выражению (8)
θ(t) = 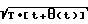 , откуда следует, что
, откуда следует, что
θ(t) = T/2 + 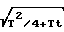 .
.
Если в выражениях (1) и (2) заменить θ на τ =const, получают дифференциальные уравнения с постоянными коэффициентами, которые обычно используют для реализации постоянной задержки. Коэффициенты в уравнении (2) несколько изменяют, пользуясь так называемым приближением Паде. Однако не существует раз и навсегда заданных наилучших значений коэффициентов. Пользуясь различными критериями оптимальности, получают различные наборы значений для коэффициентов.
При попытке в уравнения (1) и (2) вместо θ подставить переменную задержку τ (t) получают уравнения, непригодные для реализации переменной задержки τ (t). В самом деле пусть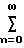 [τn(t)/n!]yn = x .
[τn(t)/n!]yn = x .
Тогда y [(t +τ (t)] =x (t);
y{t - τ (t) + τ [t- τ (t)]} = x[t- τ (t)].
Но τ(t) ≠ τ[t-τ(t)], поэтому полученное выражение не равносильно выражению (7). Теперь становится понятным, зачем в способе-прототипе непрерывный закон τ (t) аппроксимирован ступенчато изменяющейся зависимостью τ*(t) и как в предлагаемом способе удалось избежать этой погрешности.
Рассмотрим простейшие примеры реализации способа. Если в уравнении (2) ограничиться первыми двумя членами ряда Тейлора, получают дифференциальное уравнение первого порядка:
y + (θ/2) yI = x-(θ/2) xI. (9)
Это уравнение описывает работу устройства, представленного на фиг. 1, состоящего из сумматоров 1 и 2, блока 3 переменного коэффициента и интегратора 4. Инверсный вход сумматора 1 соединен с входным зажимом устройства и инверсным входом сумматора 2. Выход сумматора 1 соединен с входом блока 3 переменного коэффициента, осуществляющего перемножение входного сигнала на формируемый этим блоком переменный коэффициент 2/θ (t). Выход блока 3 соединен с входом интегратора 4, выход которого соединен с прямым входом сумматора 2. Выход сумматора 2 соединен с выходным зажимом устройства и прямым входом сумматора 1.
Пройдя от входа устройства к выходу и записав сигналы во всех точках, можно составить уравнение
y = - 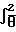 (y-x)dt-x , (10) продифференцировав обе части которого, легко убедиться в его равносильности уравнению (9).
(y-x)dt-x , (10) продифференцировав обе части которого, легко убедиться в его равносильности уравнению (9).
Если в уравнении (1) ограничиться первыми тремя членами ряда Тейлора, получают дифференциальное уравнение второго порядка:
y + θ yI + (θ2/2) yII= x (11)
Это уравнение описывает работу устройства фиг. 2, состоящего из интеграторов 5 и 6, сумматоров 7 и 8 и блоков 9 и 10 переменных коэффициентов. Вход интегратора 5 соединен с выходом сумматора 8, входы которого соединены с выходами блоков 9, 10 переменных коэффициентов. Выход интегратора 5 соединен с входом интегратора 6 и с входом блока 9 переменного коэффициента, выход интегратора 6 соединен с выходным зажимом устройства и инверсным входом сумматора 7, прямой вход которого соединен с входным зажимом устройства, а выход - с входом блока 10 переменного коэффициента.
По выходному сигналу интегратора 6 y(t) можно определить его входной сигнал [-yI (t)] и входной сигнал интегратора 5 yII (t), который, кроме того, равен выходному сигналу сумматора 8, т.е.
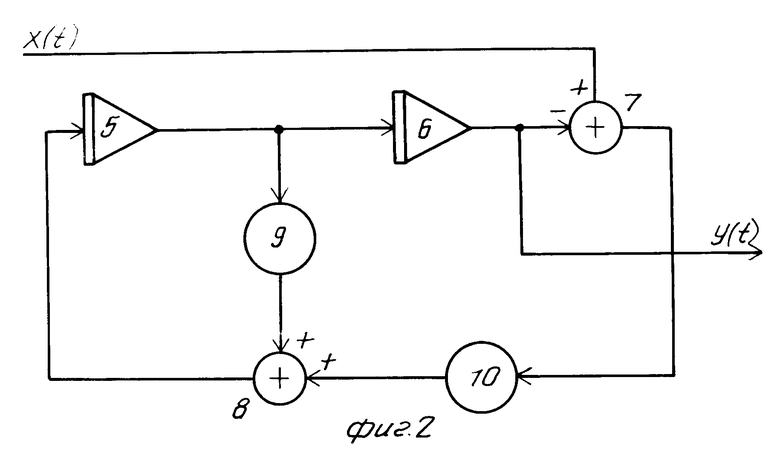
y″ = -  y′+
y′+ 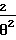 (x-y) . (12)
(x-y) . (12)
Уравнение (12) равносильно уравнению (11). Блоки 3,9 переменных коэффициентов содержат формирователь сигнала 2/θ (t) и умножитель, блок 10, кроме того, содержит квадратор.
Итак, показано, что в предлагаемом способе параметры системы, осуществляющей задержку сигнала, изменяют по закону θ (t), в точности соответствующему требуемой задержке τ (t), а в способе-прототипе параметры системы, осуществляющей задержку сигнала, изменяют по приближенному закону τ*(t). Таким образом, предлагае- мый способ точнее способа-прототипа. Следовательно, при равной точности устройств устройство, реализующее предлагаемый способ, проще и дешевле устройства, реализующего способ-прототип.
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для линейной стационарной обработки сигналов | 1987 |
|
SU1532998A1 |
| Устройство для линейной стационарной обработки сигналов | 1989 |
|
SU1721794A1 |
| Трансверсальный фильтр | 1987 |
|
SU1515350A1 |
| СИСТЕМА ИДЕНТИФИКАЦИИ ПАРАМЕТРОВ НЕСТАЦИОНАРНОГО ОБЪЕКТА С ПЕРЕМЕННЫМ ЗАПАЗДЫВАНИЕМ | 1990 |
|
RU2027214C1 |
| СИСТЕМА АДАПТИВНОГО УПРАВЛЕНИЯ НЕСТАЦИОНАРНЫМИ НЕЛИНЕЙНЫМИ ОБЪЕКТАМИ | 1990 |
|
RU2031434C1 |
| Анализатор комплексного спектра | 1988 |
|
SU1688184A1 |
| СИСТЕМА ИДЕНТИФИКАЦИИ ОБЪЕКТОВ УПРАВЛЕНИЯ | 2012 |
|
RU2486563C1 |
| Трансверсальный фильтр | 1985 |
|
SU1325673A1 |
| СИСТЕМА РЕГУЛИРОВАНИЯ ОБЪЕКТА С РЕЦИКЛОМ | 2014 |
|
RU2542910C1 |
| Формирователь группового сигнала | 1985 |
|
SU1314468A1 |
Изобретение относится к радиоэлектронике и автоматике, предназначено для получения изменяющейся во времени по известному закону задержки сигнала, может быть использовано для обработки сигналов в реальном масштабе времени и для аналогового моделирования. Целью изобретения является повышение точности. Сущность способа состоит в том, что сигнал пропускают через динамическую систему с переменными параметрами, воспроизводящую линейное дифференциальное уравнение с переменными коэффициентами, параметры системы, определяющие величину задержки сигнала, изменяют по закону θ(t) , связанному с заданной задержкой τ(t) уравнением θ[t-τ(t)] = τ(t) . 2 ил.
СПОСОБ ПЕРЕМЕННОЙ ЗАДЕРЖКИ СИГНАЛА, основанный на пропускании сигнала через динамическую систему с переменными параметрами, воспроизводящую линейное дифференциальное уравнение с переменными коэффициентами, определяющими величину задержки сигнала, отличающийся тем, что параметры системы изменяют по закону Θ(t) связанному с заданной задержкой τ(t) уравнением
Θ[t - τ(t)] = τ(t) .
| Солодов А.А., Солодова Е.А | |||
| Системы с переменным запаздыванием | |||
| М.: Наука | |||
| Главная редакция физико-математической литературы, 1980, с.316-317, рис.6.12,6.13. |
Авторы
Даты
1994-11-30—Публикация
1990-12-04—Подача