Изобретение относится к машиностроению и может быть использовано в механизмах бесшпиндельного привода рабочих валков мелкосортных и проволочных станов.
Известна эвольвентная корригированная зубчатая передача внутреннего зацепления, содержащая шестерню с внешними зубьями и колесо с внутренними зубьями.
Недостатком этой передачи является ограниченная нагрузочная способность, которая определяется крутящими моментами на колесе, допустимыми контактной выносливостью поверхностей зубьев и изгибной прочностью зубьев. Увеличение моментов, допускаемых как контактной выносливостью, так и изгибной прочностью зубьев, возможно при уменьшении разности чисел зубьев. Эта разность при стандартном исходном контуре и оптимально выбранных коэффициентах смещения не может быть меньше четырех. При этом для высоконагруженных приводов малогабаритных клетей мелкосортных и проволочных станов нагрузочная способность передачи остается недостаточной.
В таких станах межосевое расстояние передачи, обеспечивающее возможность регулировки межвалкового расстояния после переточки валков, может быть достаточно малым и составлять 3-5% диаметра валка и равного ему габаритного диаметра пояса внутреннего зацепления. При таком межосевом расстоянии модуль зацепления, равный его отношению к разности чисел зубьев, получается мелким и не обеспечивает изгибную прочность зубьев с другой стороны, увеличение межосевого расстояния сверх необходимого по условиям переточки валков приводит к уменьшению приведенного радиуса кривизны профиля зубьев и соответственно к снижению их контактной выносливости.
Из известных эвольвентных передач внутреннего зацепления наиболее близкой по технической сущности является передача, содержащая шестерню и колесо с коррегированными и равными между собой числами зубьев.
Недостаток этой передачи состоит в том, что ее геометрические параметры жестко связаны со способом образования сопряженных профилей зубьев путем огибания их стандартным исходным контуром при различных по величине и знаку, но только радиальных смещениях. При этом требуемая для заданного межосевого расстояния алгебраическая разность величин смещения втрое превышает величину, достаточную для обеспечения радиального зазора. Неоправданное уменьшение рабочей глубины захода зубьев по отношению к их полной высоте снижает, во-первых, изгибочную прочность зубьев (за счет удаления геометрического места точек приложения усилий от корня зуба) и, во-вторых, контактную выносливость (за счет уменьшения длины рабочего участка линии зацепления и смещения его в зону неблагоприятного сочетания радиусов кривизны профилей).
Целью изобретения является повышение нагрузочной способности передачи при заданном межосевом расстоянии.
Это достигается тем, что в эвольвентной зубчатой корригированной передаче внутреннего зацепления, содержащей шестерню и колесо с равными между собой числами соответственно внешних и внутренних зубьев, параметры колес определяют по зависимостям
δ = φ-μ1-μ2-inv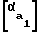 +inv
+inv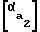
δ = 2∈·φ-tg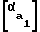 +tg
+tg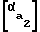 , где δ =
, где δ = 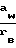 - относительный эксцентриситет;
- относительный эксцентриситет;
aw - межосевое расстояние;
φ =  - половина углового шага зубьев;
- половина углового шага зубьев;
αa1αa2 - углы профиля на окружностях вершин соответственно шестерни и колеса;
μ1= 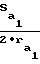 ≈ 0,1φ ; μ2=
≈ 0,1φ ; μ2= 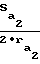 ≈ 0,06·φ половина угловых толщин зубьев на поверхностях вершин соответственно шестерни и колеса;
≈ 0,06·φ половина угловых толщин зубьев на поверхностях вершин соответственно шестерни и колеса;
r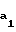 =
= 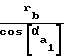 ; r
; r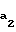 =
= 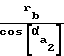 радиусы окружностей вершин шестерни и колеса;
радиусы окружностей вершин шестерни и колеса;
Sa1;Sa2- толщина зубьев на поверхностях вершин шестерни и колеса;
∈ - торцевой коэффициент перекрытия.
Величина радиального смещения исходного контура зубьев шестерни и колеса определяется соответственно из соотношения
x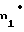 m = 1,05m+
m = 1,05m+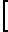 r
r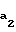 -aw-
-aw-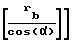
x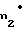 m =
m = 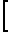 r
r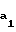 +aw-
+aw-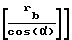 -1,05·m, где α - угол исходного контура, а зубья шестерни и колеса выполнены с дополнительным тангенциальным смещением исходного контура и величина этого смещения выбрана соответственно равной
-1,05·m, где α - угол исходного контура, а зубья шестерни и колеса выполнены с дополнительным тангенциальным смещением исходного контура и величина этого смещения выбрана соответственно равной
x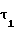 = 0,5π+2x
= 0,5π+2x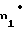 tgα-z
tgα-z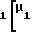 -inv(α)+inv
-inv(α)+inv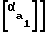
x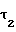 = 0,5π-2x
= 0,5π-2x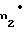 tgα+z
tgα+z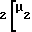 -inv(α)+inv
-inv(α)+inv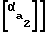
Радиус основной окружности выполнен равным
rb = aw ˙ctg[0,84 φ-inv(δ)]
Радиус окружности вершин колеса выполнен равным
r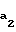 =
= 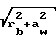
Радиус окружности вершин шестерни выполнен равным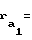
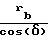
Коэффициент перекрытия может быть принят равным 2,0...2,1, а числа зубьев шестерни и колеса выполнены в пределах 23...27 или коэффициент перекрытия может быть принят равным 1,0...1,1, а числа зубьев шестерни и колеса выполнены в пределах 7...9.
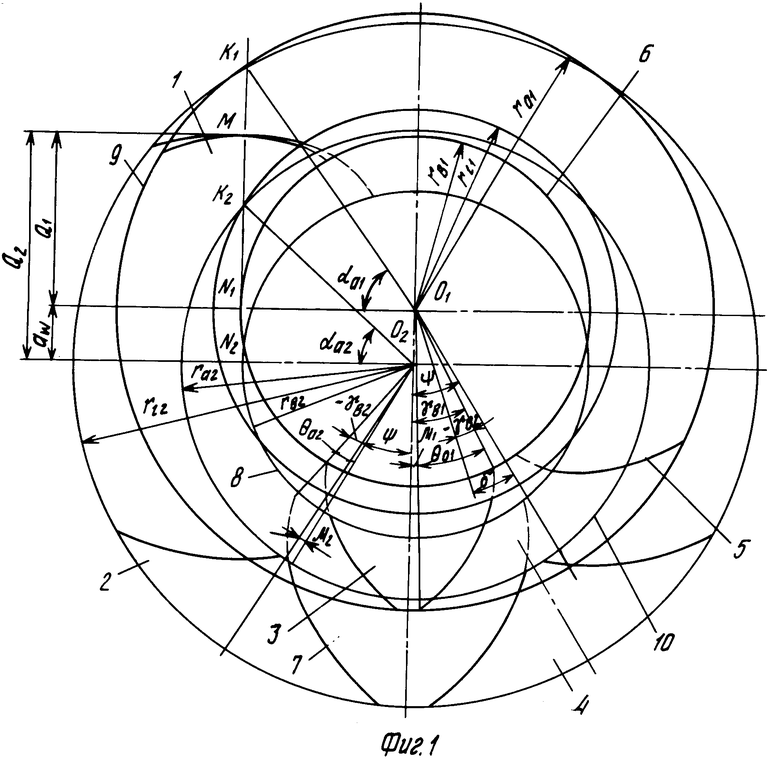
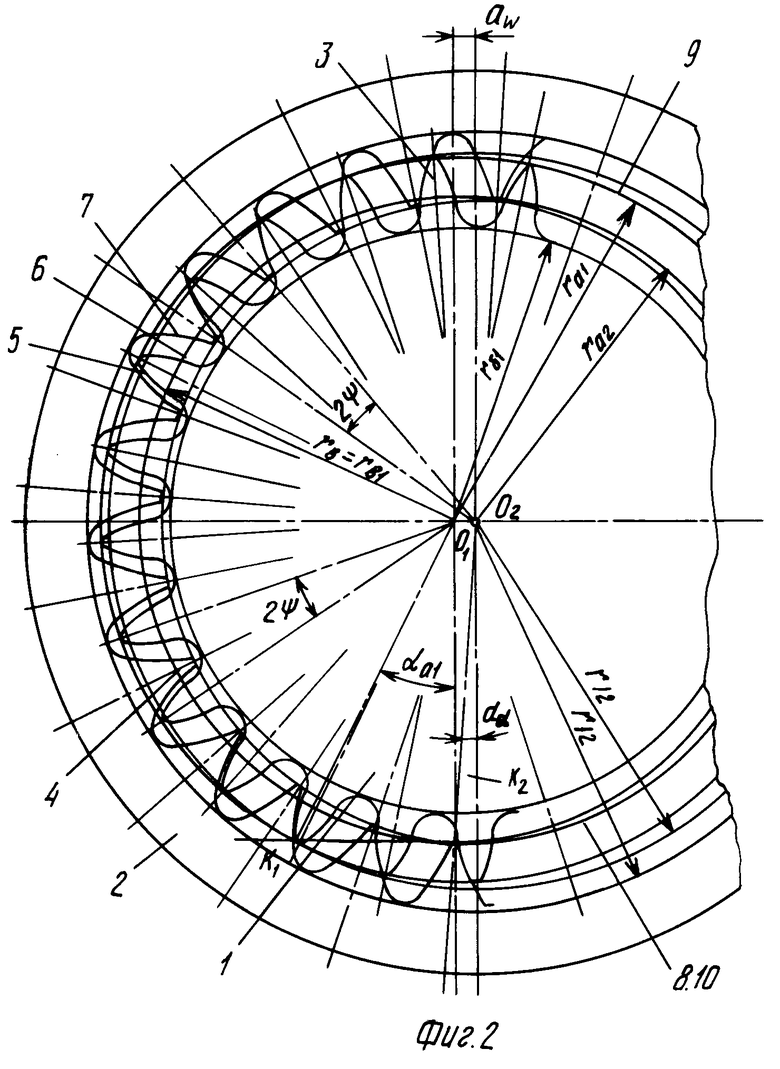
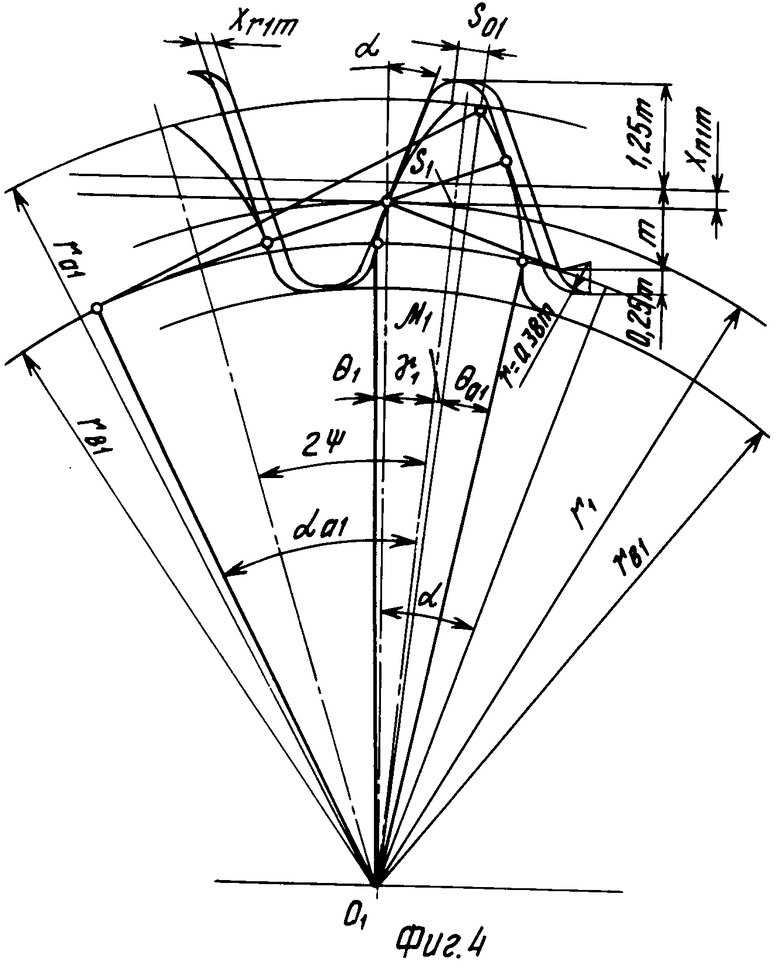
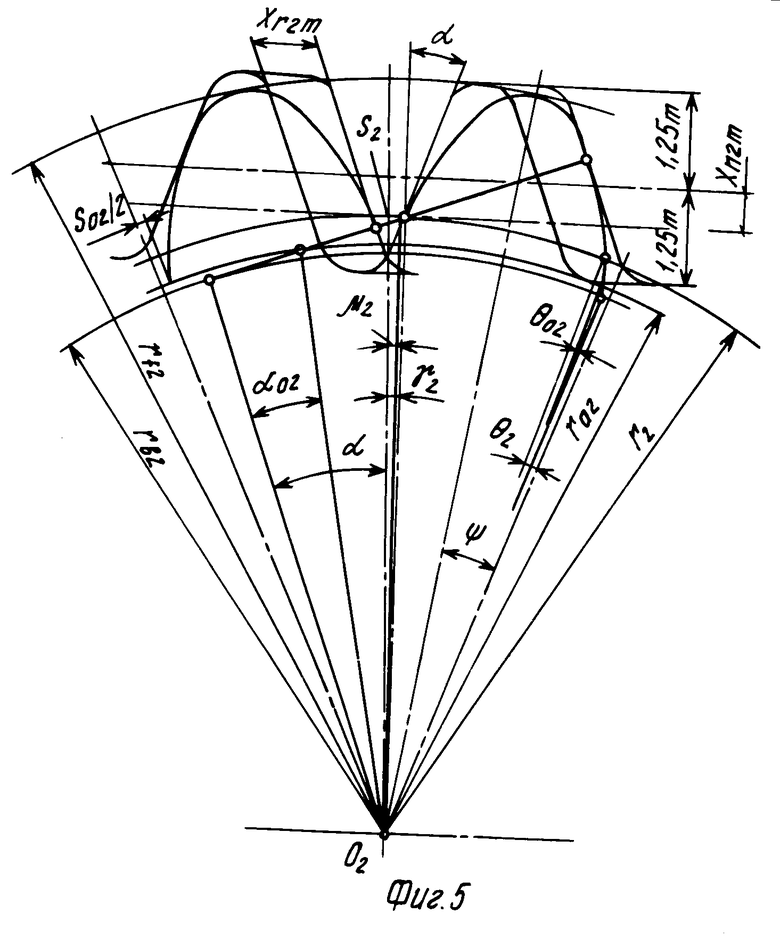
На фиг. 1 схематично изображена предлагаемая передача, общий вид; на фиг. 2 - конкретный пример выполнения передачи согласно п.4 формулы изобретения; на фиг.3 - то же, согласно п.5 формулы изобретения; на фиг.4 изображен зуб шестерни и схема его образования при использовании стандартного исходного контура; на фиг.5 - зуб колеса и схема его образования при использовании стандартного исходного контура.
Передача внутреннего эвольвентного зацепления состоит из шестерни 1 и колеса 2. Центр шестерни 01 смещен относительно центра колеса 02 на межосевое расстояние aw. Шестерня 1 снабжена внешними корригированными эвольвентными зубьями 3, колесо 2 - внутренними корригированными эвольвентными зубьями 4. Число зубьев шестерни равно числу зубьев колеса (Z1 = Z2 = =Z). Рабочие участки боковых профилей зубьев шестерни очерчены эвольвентами 5 основной окружности 6 радиуса rb1. Рабочие участки боковых профилей зубьев колеса очерчены эвольвентами 7 основной окружности 8 того же радиуса rb2= rb1 = rb. Зубья 3 шестерни 1 ограничены окружностью вершин 9 радиуса ra1. Зубья 4 колеса 2 ограничены окружностью вершин 10 радиуса ra2. Со стороны тела зуба шестерни и колеса эвольвентные рабочие участки профиля ограничены радиусами соответственно rl1иrl2. Впадины зубьев ограничены радиусами rf1иrf2.
Условием сопряженности эвольвентной передачи является равенство основных шагов (шагов зацепления) шестерни и колеса Pb1=Pb2=Pb=π rb/Z.
Линия зацепления - общая касательная к основным окружностям, параллельная линии центров.
Рабочий участок линии зацепления К1К2 определяется точками ее пересечения с окружностями вершин колеса К2 и шестерни К1. Длина этого участка определяется как K1K2= K1N1+N1N2-K2N2= rb·tg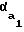 +aw-rbtg
+aw-rbtg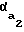 (1) где αa1 - угол профиля на окружности вершин шестерни;
(1) где αa1 - угол профиля на окружности вершин шестерни;
αa2 - угол профиля на окружности вершин колеса;
N1N2 - точки касания линии зацепления с основными окружностями шестерни и колеса.
Отношение длины рабочего участка линии зацепления к шагу зацепления представляет собой коэффициент перекрытия ε = К1К2/Pb. Если обозначить относительный эксцентриситет aw/rb = δ и угловой шаг колеса Pb/rb = 2 Φ, то из уравнения (1)
δ = 2εφ-tg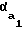 +tg
+tg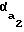 (2)
(2)
Половину угловой толщины зубьев на окружности вершин шестерни обозначим μ1, а колеса μ2.
Тогда на основной окружности половина угловой толщины зуба шестерни равняется (см. фиг.1):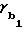 = μ1+
= μ1+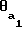 , (3) где
, (3) где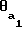 = inv
= inv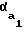 = tg
= tg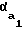 -
- 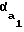
Аналогично для колеса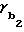 = μ2-
= μ2-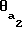 , (4) где
, (4) где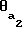 = inv
= inv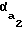 = tg
= tg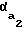 -
- 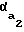
Величина rb[ Φ-(γb1+γb2)] определяет собой нормальный зазор между зубьями в том случае, если центры шестерни и колеса совмещены между собой, т.е. максимальное межосевое расстояние aw, на которое могут быть смещены эти центры до того, как нерабочие профили зубьев соприкоснутся друг с другом, будет равно
aw= r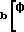 -
-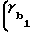 +
+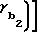 (5)
(5)
Разделив обе части выражения (3) на rb и раскрыв γb1 и γb2, получим значение относительного эксцентриситета
δ = φ-μ1-μ2-inv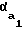 +inv
+inv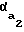 (6)
(6)
Уравнения (2) и (6) должны соблюдаться в любой передаче, изготовленной в соответствии с изобретением. Но в эти уравнения входят шесть конструктивных параметров (δ,Φ,μ1,μ2,αa1,αa2) и коэффициент перекрытия ε , следовательно, пять параметров остаются свободными. Если задаться значениями μ1иμ2 , то свободными остаются еще три параметра, которыми можно варьировать, обеспечивая оптимизацию передачи. В частности, для быстроходных передач необходимо стремиться к максимальному коэффициенту перекрытия, в других случаях при минимальном коэффициенте перекрытия добиваться минимизации габаритов передачи и т.д.
При заданной высоте зуба коэффициент перекрытия ε увеличивается с уменьшением угла αa2. Минимальное значение этого угла, а следовательно максимальный коэффициент перекрытия имеют место при совпадении границ К2и N1 рабочего и теоретического участков линии зацепления. В этом случае tg αa2= δ, тогда из уравнения (2) tg αa1=2εΦ
Подставив эти два выражения в уравнение (6) и принимая значения μ1= 0,1 Φ и μ2 =0,06Φ , получим
arctgδ=0,84Φ-invarctg2εΦ (7)
Отсюда по заданному межосевому расстоянию находим требуемый радиус основной окружности
rb=awctg[arctg2εΦ-(2ε-0,84)Φ] (8)
Радиус окружности вершин зубьев колеса в этом случае следует выполнить равным
r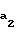 = rb/cos
= rb/cos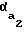 =
= 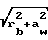 (9)
(9)
Радиус окружности вершин зубьев шестерни
r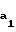 = rb/cos
= rb/cos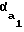 = rb/cosarctg2εφ (10)
= rb/cosarctg2εφ (10)
При заданном aw передача будет иметь минимальные габариты в том случае, когда относительный эксцентриситет δ имеет возможно большое значение. Согласно выражению (7) δ зависит от двух параметров: Φи ε . Для того, чтобы при выбранном ε определить то значение Φ , при котором δ достигает максимума, необходимо продифференцировать выражение (10) по Φ и приравнять производную нулю. После преобразований получим
2ε /(1 + 4ε2Φ2) = 2 ε - 0,84
Откуда: φ =  2ε (11)
2ε (11)
Выбор желательного значения коэффициента перекрытия определяется условиями работы передачи. Для быстроходных передач важнейшим требованием является плавность работы передачи и в этом случае число одновременно работающих зубьев должно быть не меньше двух. Приняв ε = =2,02 из выражения (11) находим Φ = 0,1268, чему соответствует Z =π /Φ= 24,77. Исследование функции δ= δ (Z) показало, что ее оптимум является весьма пологим и целочисленные значения Z могут выбираться в пределах 23 и 27 зубьев. При этом относительный эксцентриситет δ = 0,067, т.е. межосевое расстояние, составляет 1/30 диаметра основной окружности или ≈1,25 основного модуля.
Для тихоходных высоконагруженных передач достаточно, чтобы коэффициент перекрытия превышал единицу. Приняв ε = 1,02, из выражения (11) находим Φ = 0,4101 и Z = 7,66.
Отсюда целочисленные значения Z, обеспечивающие минимальные габариты передачи, могут выбираться в пределах 7...9 зубьев. При этом относительный эксцентриситет δ = 0,2, т.е. aw составляет 0,1 диаметра основной окружности или 0,8 модуля. Уменьшение числа зубьев по сравнению с рассмотренным случаем резко увеличивает модуль и вместе с ним изгибную прочность зуба в тех же габаритах передачи.
Наиболее технологичным способом получения зубьев шестерни 1 является нарезание их реечным инструментом, например червячной фрезой со стандартным исходным контуром. Однако для обеспечения требуемых по изобретению размеров зуба исходный контур при обработке должен быть смещен от своего номинального положения, причем не только в радиальном, как это имеет место в известных корригированных передачах, но и в тангенциальном по отношению к шестерне направлении.
Определим требуемые коэффициенты радиального Хn1 и тангенциального Xr1 смещений исходного контура при обработке шестерни.
Из условия обеспечения в собранной передаче радиального зазора С = 0,2m, где m - модуль зацепления, радиус впадин шестерни определяем как
r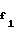 = r
= r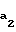 -aw-c (12)
-aw-c (12)
С другой стороны
r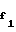 = r1-(1,25-x
= r1-(1,25-x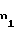 )m , (13) где r1 = 0,5mZ1 - делительный радиус;
)m , (13) где r1 = 0,5mZ1 - делительный радиус;
1,25m - высота делительной шестерни головки зуба исходного контура.
Учитывая, что делительный радиус шестерни связан с радиусом ее основной окружности зависимостью
r1 = rb/cos α , (14) где α = 20о - делительный угол профиля зуба, приравняем выражения (12) и (13) и после преобразований получим
x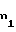 = 1,05+
= 1,05+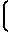 r
r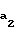 -aw-r
-aw-r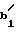 cos
cos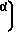 /m (15)
/m (15)
Коэффициент Xτ1 тангенциального смещения исходного контура определяет изменение делительной толщины S1 зуба шестерни
s1= m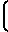 0,5π+2x
0,5π+2x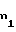 tgα-x
tgα-x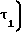 (16)
(16)
Выразив через S1 половину угловой толщины зуба шестерни по основной окружности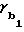 = s1/2r1+θ1, (17) где θ= invα, и приравняв между собой выражения (3) и (17) с учетом выражения (16), после преобразований найдем требуемое значение Xτ1 x
= s1/2r1+θ1, (17) где θ= invα, и приравняв между собой выражения (3) и (17) с учетом выражения (16), после преобразований найдем требуемое значение Xτ1 x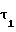 = 0,5π+2x
= 0,5π+2x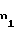 tgα-z
tgα-z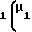 -invα+inv
-invα+inv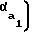 (18)
(18)
Внутренние зубья колеса 2 могут быть нарезаны зуборезным долбяком или получены протягиванием, но в любом случае размеры этих зубьев вполне определяются параметрами исходного контура и коэффициентами его нормального Хn2 и тангенциального Xτ2 смещения.
Повторив для зуба колеса математические выкладки, приведенные для зуба шестерни, требуемые значения коэффициентов смещения получим в виде x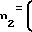 r
r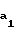 +aw-rb/cos
+aw-rb/cos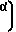 /m-1,05 (19) x
/m-1,05 (19) x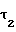 = 0,5π+2x
= 0,5π+2x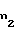 tgα+z
tgα+z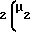 +invα-inv
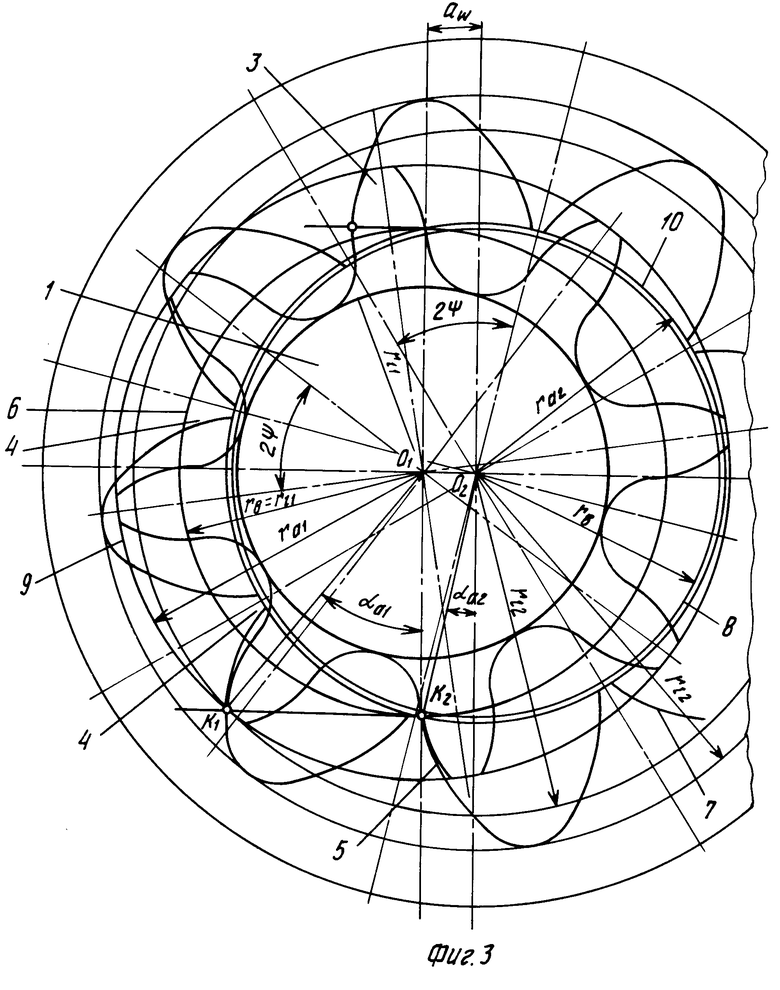
+invα-inv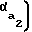 (20) Устройство работает следующим образом.
(20) Устройство работает следующим образом.
При сборке передачи внутреннего эвольвентного зацепления шестерня 1 с внешними зубьями 3 вводится в зацепление с внутренними зубьями 4 колеса 2, передавая вращение с ведущего вала на ведомый путем взаимодействия зубьев колеса и шестерни.
Передаточное число равно единице. Мгновенная точка контакта профилей μ перемещается по линиям зацепления, общей касательной к основным окружностям, параллельной линии центров. Угол зацепления составляет 90о. Полюс зацепления, который должен лежать на пересечении линии зацепления с межосевой линией передачи, уходит в бесконечность. Рабочий участок линии зацепления определяется точками ее пересечения с окружностями вершин колеса и шестерни.
В передаче, представленной на фиг.2, в контакте одновременно находятся два или три зуба, в варианте, представленном на фиг.3, - один или два зуба.
Нагрузочная способность передачи определяется крутящим моментом на колесе, допускаемым контактной выносливостью поверхностей зубьев и их изгибной прочностью. При этом расчет на изгибную прочность вполне аналогичен расчету обычных передач внутреннего зацепления, но требует определения коэффициентов формы зуба с учетом величины тангенциального смещения. При расчете на контактную выносливость в качестве опасной точки вместо полюса зацепления следует рассматривать ближайшую к основным окружностям границу одно- или двухпарного зацепления.
| название | год | авторы | номер документа |
|---|---|---|---|
| АРОЧНАЯ ЗУБЧАТАЯ ПЕРЕДАЧА И СПОСОБ ЕЕ ИЗГОТОВЛЕНИЯ | 1995 |
|
RU2092725C1 |
| СПОСОБ УСТАНОВЛЕНИЯ УГЛА ГЛАВНОГО ПРОФИЛЯ ИСХОДНОГО ПРОИЗВОДЯЩЕГО РЕЕЧНОГО КОНТУРА И КОЭФФИЦИЕНТА ЕГО СМЕЩЕНИЯ ПРИ НАРЕЗАНИИ ПРЯМОЗУБЫХ ЗУБЧАТЫХ КОЛЕС С МАЛЫМ ЧИСЛОМ ЗУБЬЕВ ВНЕШНЕЙ ЭВОЛЬВЕНТНОЙ ПЕРЕДАЧИ С ПЕРЕДАТОЧНЫМ ОТНОШЕНИЕМ, РАВНЫМ ЕДИНИЦЕ | 1998 |
|
RU2143622C1 |
| МОДИФИЦИРОВАННАЯ ЭВОЛЬВЕНТНАЯ ЗУБЧАТАЯ ПЕРЕДАЧА | 1997 |
|
RU2128303C1 |
| ГИПОИДНАЯ ПЕРЕДАЧА | 1991 |
|
RU2019762C1 |
| СПОСОБ ФОРМООБРАЗОВАНИЯ АРОЧНЫХ ЗУБЬЕВ ЦИЛИНДРИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС | 1994 |
|
RU2074062C1 |
| КОСОЗУБАЯ ЗУБЧАТАЯ ПЕРЕДАЧА | 2002 |
|
RU2222738C1 |
| СПОСОБ ОБРАБОТКИ ЭВОЛЬВЕНТНЫХ ПРОФИЛЕЙ КРУГОВЫХ ЗУБЬЕВ ЦИЛИНДРИЧЕСКИХ КОЛЕС | 1992 |
|
RU2049608C1 |
| ПРЯМОЗУБАЯ ЗУБЧАТАЯ ПЕРЕДАЧА | 1999 |
|
RU2160403C1 |
| ЗУБЧАТАЯ ПЕРЕДАЧА | 1995 |
|
RU2108509C1 |
| СПОСОБ ОБРАЗОВАНИЯ ЗУБЧАТЫХ ПЕРЕДАЧ ДВУХПОЗИЦИОННЫМ ОБКАТОМ | 2009 |
|
RU2412026C2 |
Изобретение предназначено для механизмов бесшпиндельного привода сближающихся между собой по мере переточки рабочих валков прокатных станов, в особенности мелкосортных и проволочных. Предлагаемая передача содержит шестерню и колесо с равными числами внешних и внутренних зубьев. В такой передаче полюс зацепления уходит в бесконечность, угол зацепления равен 90°, линия зацепления параллельна линии центров, а межосевое расстояние равно половине бокового зазора, измеренного по нормали к эвольвентному профилю. При обработке зубьев каждого колеса стандартным зуборезным инструментом предложено в дополнение к радиальному ввести тангенциальное смещение исходного контура, что позволяет увеличить глубину захода зубьев и оптимизировать передачу по критериям плавности и/или нагрузочной способности. В частности предложены варианты передачи с гарантированным двухпарным зацеплением и с минимальными для заданного межосевого расстояния габаритами. 4 з.п.ф-лы, 5 ил.
δ = Φ - μ1 - μ2 - inv [αa1]+ inv [αa2] ,
δ = 2∈·φ-tg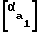 +tg
+tg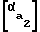 ,
,
где δ = 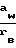 - относительный эксцентриситет;
- относительный эксцентриситет;
aw - межосевое расстояние;
rb - радиус основной окружности;
φ =  - половина углового шага зубьев;
- половина углового шага зубьев;
αa1 ; αa2 - углы профиля на окружности вершин соответственно шестерни и колеса;
μ1= 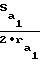 ≈ 0,1φ , μ2=
≈ 0,1φ , μ2= 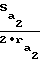 ≈ 0,06·φ - половина угловых толщин зубьев на поверхностях вершин соответственно шестерни и колеса;
≈ 0,06·φ - половина угловых толщин зубьев на поверхностях вершин соответственно шестерни и колеса;
r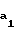 =
= 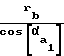 ; r
; r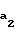 =
= 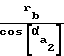 - радиусы окружностей вершин шестерни и колеса;
- радиусы окружностей вершин шестерни и колеса;
sa1 ; sa2 - толщина зубьев на поверхностях вершин шестерни и колеса;
∈ - торцовый коэффициент перекрытия.
x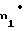 m = 1,05m+
m = 1,05m+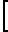 r
r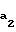 -aw-
-aw-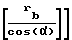
x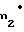 m =
m = 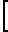 r
r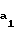 +aw-
+aw-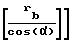 -1,05·m
-1,05·m
где α - угол исходного контура,
а зубья шестерни и колеса выполнены с дополнительным тангенциальным смещением исходного контура и величина этого смещения выбрана соответственно равной
xτ1 = 0,5π - 2xn1˙tgα-z1[μ1-inv(α)+
+inv(αa1)] ,
xτ2 = 0,5π + 2xn2˙tgα+z2[μ2-inv(α)+
+inv(αa2)] .
радиус окружности вершин шестерни выполнен равным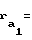
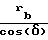 .
.
4. Передача по пп. 1 - 3, отличающаяся тем, что коэффициент перекрытия принят равным 2,0 - 2,1, а число зубьев шестерни и колеса - в пределах 23 - 27.
| Цилиндрические эвольвентные зубчатые передачи внутреннего зацепления | |||
| Справочное пособие, М.: 1977, с.131. |
Авторы
Даты
1994-12-30—Публикация
1991-01-02—Подача