Изобретение относится к машиностроению, а точнее к конструкциям гипоидной передачи, и может быть использовано в трехвалковом стане винтовой прокатки.
Разновидностью таких станов являются планетарные станы винтовой прокатки, в которых относительное движение валка, складываясь с переносным движением вращающейся клети, приводит к поступательному движению прокатываемого изделия без его вращения. Каждый из трех валков стана приводится во вращение от центрального колеса, ось которого совпадает с осью прокатки. Ось самого валка смещена относительно оси прокатки на полусумму диаметров заготовки и валка и составляет с ней угол, обеспечивающий продольную подачу заготовки. Такое относительное движение валка в известных станах обеспечивается различными комбинациями цилиндрических и конических передач. Но целесообразней использовать неортогональную гипоидную передачу, от центрального колеса которой вращение передается трем шестерням, непосредственно установленным на рабочих валках. Известна гипоидная передача, содержащая конические шестерню и колесо, нарезаемые плоским производящим колесом с круглой резцовой головкой и установленные на взаимно ортогональных осях с произвольным гипоидным смещением. В торцовом сечении зубья выполнены по типу зацепления Новикова, то есть очерчены плавно сопряженными между собой дугами окружностей. В продольном направлении зубья выполнены круговыми, равновысокими, что органически обусловлено криволинейностью профилирующих резцов резцовой головки.
При этом образующие начальных конусов шестерни и колеса должны быть равны между собой и равны радиусу общего для них плоского производящего колеса, что существенно осложняет наладку зуборезного станка.
Недостатком этой передачи является низкая нагрузочная способность этой передачи, которая объясняется низкой изгибной прочностью зубьев зацепления и повышенной по отношению к квазиэвольвентным передачам чувствительностью к погрешностям изготовления и монтажа.
Из известных гипоидных передач с произвольным углом скрещивания осей наиболее близкой по технической сущности является передача, содержащая коническую шестерню и коническое колесо с круговыми равнопонижающимися квазиэвольвентными зубьями, выполненными методом обкатки плоским производящим колесом, снабженным круглой резцовой головкой с прямобочными резцами. Средний радиус r1 шестерни и средний радиус r2 колеса связаны между собой зависимостью
r1 = К˙r2/U, где U - передаточное число, K - коэффициент увеличения размеров шестерни, выбираемый в зависимости от передаточного числа и коэффициента гипоидного смещения в пределах 1,05-1,45. Выбор коэффициента К однозначно определяет, с одной стороны, значение углов наклона зуба на шестерне и колесе, а с другой стороны, в совокупности с требованием получения равнопонижающегося зуба определяет потребный радиус резцовой головки.
Передача такой конструкции имеет относительно небольшие размеры и успешно применяется в автомобилестроении в качестве главной передачи заднего моста. Недостаток такой гипоидной передачи заключается в том, что она не обеспечивает достаточную нагрузочную способность из-за геометрических параметров и равнопонижающейся формы зуба. Поэтому для привода металлургического оборудования ее использовать нецелесообразно. Попытка увеличения нагрузочной способности путем увеличения габаритов при сохранении равнопонижающейся формы зуба приводит к значениям номинального диаметра резцовой головки, значительно превышающим технологические возможности отечественных зуборезных станков, у которых максимальный диаметр резцовой головки составляет 800 мм.
Целью настоящего изобретения является повышение нагрузочной способности гипоидной передачи путем получения квазиэвольвентных круговых равновысоких зубьев шестерни и колеса.
Поставленная цель достигается тем, что в гипоидной передаче, содержащей конические шестерни и колесо с квазиэвольвентными круговыми зубьями, согласно изобретению, зубья колеса выполнены равновысокими, центр кривизны продольной линии зуба колеса расположен на окружности, диаметром которой служит образующая R2 начального конуса, угол наклона зуба колеса в средней точке β2 выполнен равным
β2= arcsin(ru/R2), где ru - радиус кривизны продольной линии зуба колеса, причем угол наклона зуба шестерни β1 выполнен большим угла β2 на величину
μ= arcsin(aw/R2), где aw - гипоидное смещение, кроме того, начальный диаметр шестерни d1 связан с начальным диаметром колеса d2 соотношением
d1 = d2 cos β2 /U . cos β1 , где U - передаточное число.
Такое конструктивное выполнение гипоидной передачи позволяет повысить нагрузочную способность за счет увеличения ее размеров и изменения формы зуба на квазиэвольвентную равновысокую, вследствие чего контакт становится линейным и нагрузка распределяется по всей длине зуба, что повышает его контактную выносливость и изгибную прочность. Возможность увеличения габаритов в свою очередь обеспечивается за счет такого изменения осевой формы зубьев, углов их наклона и соотношения диаметров шестерни и колеса, при котором отношение диаметра резцовой головки к диаметру колеса уменьшается по сравнению с известными передачами в несколько раз, что и позволяет изготовить крупногабаритную передачу на существующем оборудовании, обеспечив при этом величины крутящих моментов, достаточные для приводов прокатного оборудования.
Среди совокупности признаков, отличающих предлагаемое изобретение от прототипа - гипоидной передачи с равнопонижающимися зубьями, имеется один признак - равновысокая осевая форма зуба колеса, сходный с осевой формой Ш (согласно ГОСТ 19326-73) круговых квазиэвольвентных зубьев колеса и шестерни конической передачи с пересекающимися осями. Такое выполнение зуба колеса конической передачи позволяет достичь того же технического эффекта - уменьшения диаметра резцовой головки по отношению к диаметру колеса, что и в предлагаемом решении.
Однако указанный признак недостаточен для синтеза гипоидной передачи и образует нераздельную совокупность с остальными признаками предлагаемого решения, а именно выполнением углов наклона зубьев колеса и шестерни не равными между собой, а начального диаметра шестерни большим отношения диаметра колеса к передаточному числу в соответствии с приведенными в формуле изобретения математическими зависимостями. С учетом изложенного, а также того, что данный признак отсутствует в прототипе, авторы включили его в отличительную часть формулы изобретения.
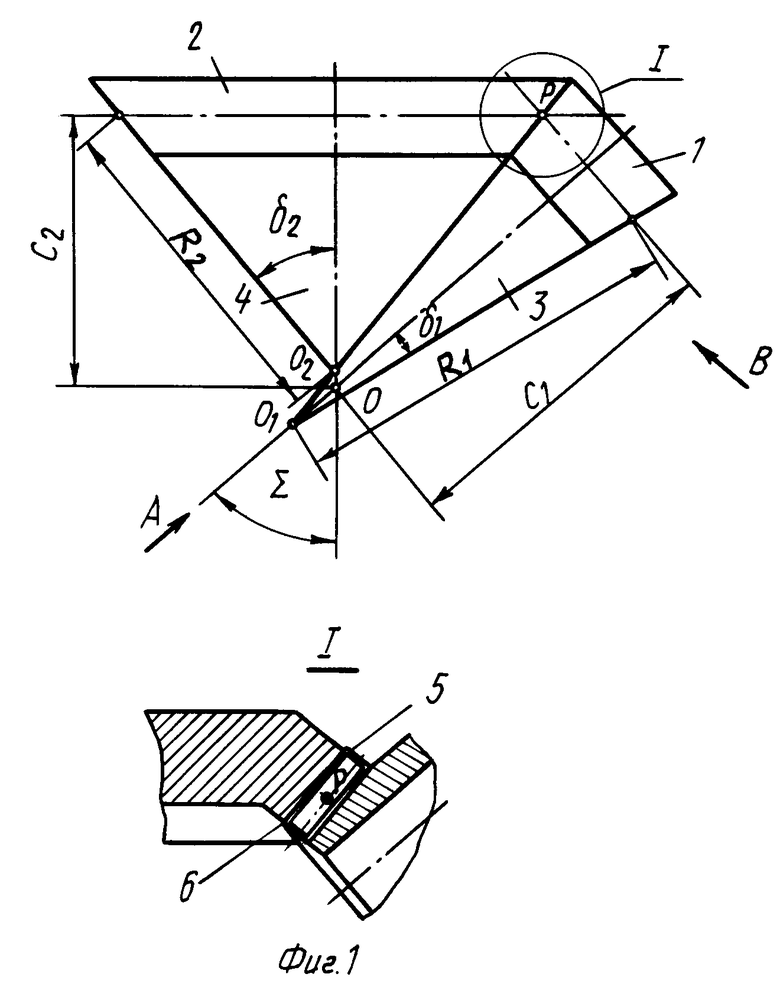
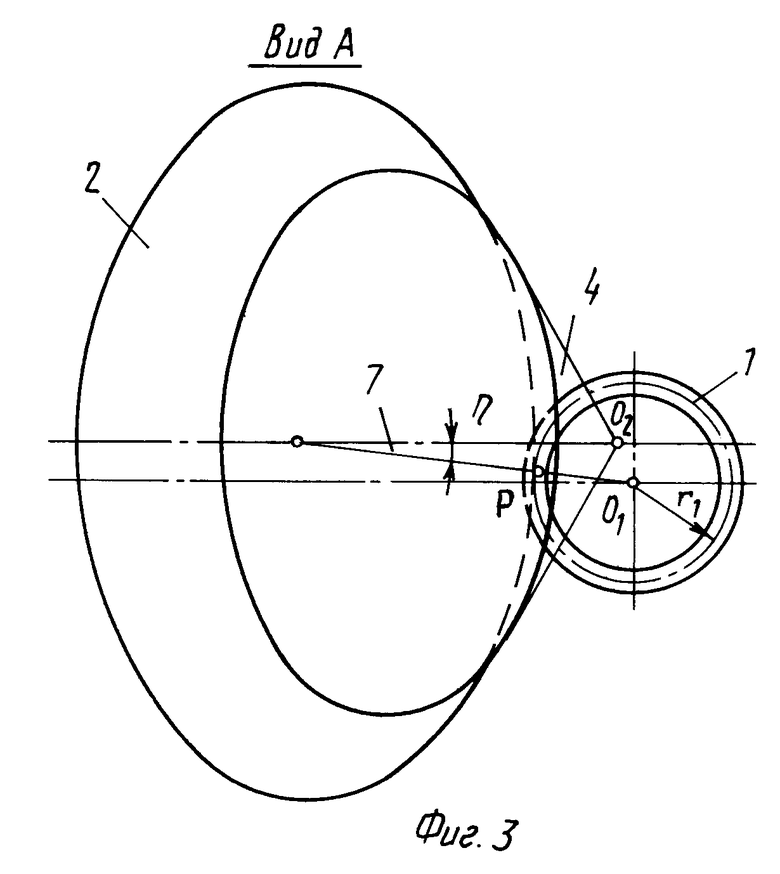
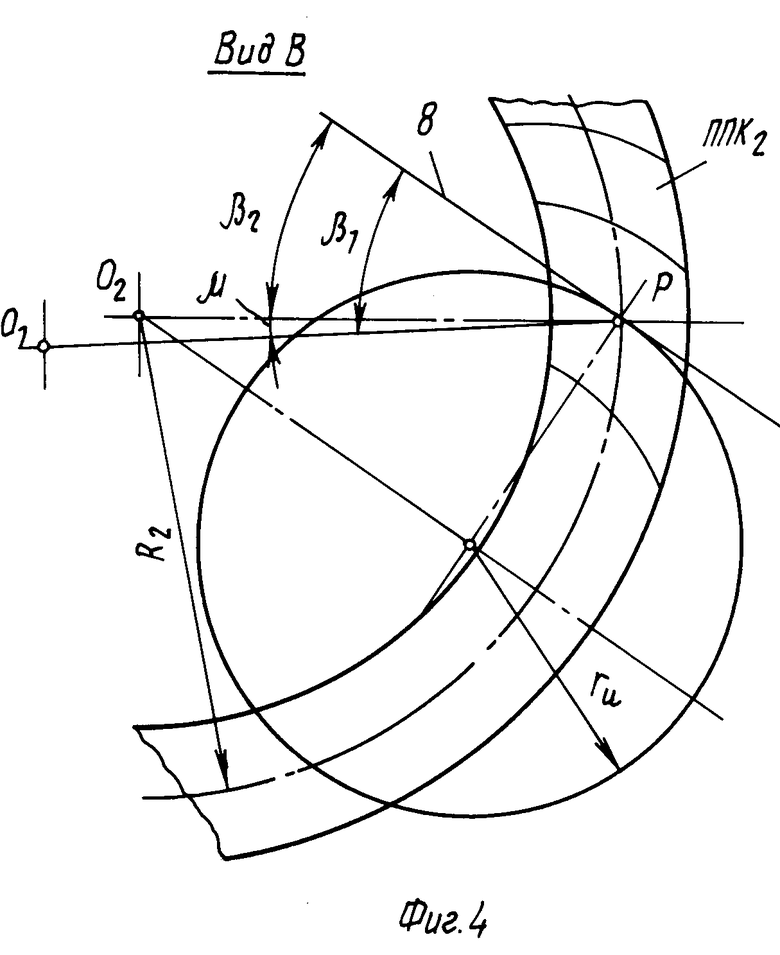
На фиг. 1 изображена гипоидная передача в плоскости, перпендикулярной линии кратчайшего расстояния между осями конусов шестерни и колеса; на фиг. 2 - предлагаемая передача в плоскости, перпендикулярной оси колеса и проходящей через вершину О1; на фиг.3 - предлагаемая передача в плоскости, перпендикулярной оси шестерни и проходящей через вершину О2, вид по стрелке А на фиг.1; на фиг.4 - вид по стрелке В на фиг.1.
Гипоидная передача состоит из конической шестерни 1 и конического колеса 2. Ось шестерни расположена относительно оси колеса 2 с гипоидным смещением aw под произвольным углом скрещивания Σ . Начальные конусы 3 шестерни 1 и 4 колеса 2 касаются друг друга в точке Р, которая принимается за среднюю точку квазиэвольвентного зуба 6 колеса 2. Вершины начальных конусов шестерни 1 и колеса 2 расположены соответственно в точках О1 и О2. Точкой 0 на фиг.1 показана проекция на плоскость чертежа линии кратчайшего межосевого расстояния.
Расстояние от плоскости среднего диаметра шестерни до линии кратчайшего межосевого расстояния - С1. Расстояние от плоскости среднего диаметра колеса до той же линии - С2. Образующая начального конуса 3 составляет с осью шестерни 1 угол δ1 , а образующая начального конуса ϕ составляет с осью колеса 2 угол δ2. Длины образующих начальных конусов 3 и 4 соответственно R1 и R2. Oбразующие начальных конусов 3 и 4, проходящие через т.Р, образуют угол μ (рис.2). Проекция общей нормали 7 к поверхностям начальных конусов 3 и 4 образует с горизонтальной плоскостью угол ε (на фиг.2) и угол η (на фиг.3). Продольная линия зуба колеса очерчена дугой радиуса ru. Касательная 8 к ней в точке Р составляет с образующими начальных конусов 3 и 4 углы β1 и β2 соответственно. Центр С кривизны продольной линии зуба расположен на окружности 9, диаметром которой служит образующая R2 начального конуса колеса 2, причем эта образующая совпадает с радиусом плоского производящего колеса ППК2, которому принадлежит резцовая головка радиуса ru. Основные параметры гипоидной передачи связаны между собой следующими зависимостями (см. стр. 10-20 книги К.М.Писманика "Гипоидные передачи")
awctg η = r2(tg δ2 - sin Σ + cos Σ ) + r1.cos η ,
(1)
sin ε . cos δ2 = tg η . cos( Σ - δ2), (2) sin δ = sin Σ cosε . cos δ2 - cosΣ . sin δ2 , (3)
sin μ - cos δ1 = sin Σ . sin ε , (4)
μ = β1 - β2 , (5)
K = cos β2/cos β1 , (6)
K = r1. U/r2, (7)
K = R1/R2, (8)
R2 = r2/sin δ2 , (9)
R1 = r1/sin δ , (10) где r1 - средний радиус шестерни,
r2 - средний радиус колеса,
K - коэффициент увеличения размеров шестерни,
U - передаточное число передачи, U = =Z2/Z1
Z1 - число зубьев шестерни,
Z2 - число зубьев колеса.
В эти десять зависимостей входит пятнадцать параметров.
Из них четыре: Σ ; aw; r2; U - являются заданными, десять - связаны, а еще один остается свободным.
В известных передачах таким параметром рассматривается коэффициент увеличения размеров шестерни К. В этом случае решение системы приведенных выше уравнений приводит к получению передачи относительно небольших размеров с равнопонижающимися зубьями, что обуславливает нагрузочную способность, недостаточную для высоконагруженных приводов прокатного оборудования.
Попытка увеличения нагрузочной способности путем увеличения геометрических параметров приводит к увеличению номинального радиуса резцовой головки, являющегося одновременно радиусом кривизны продольной линии зуба колеса, до значений, значительно превышающих технологические возможности отечественных зуборезных станков.
С целью получения крупногабаритной передачи, обладающей достаточной для привода прокатного оборудования нагрузочной способностью, зуб колеса должен быть выполнен равновысоким, что позволяет обеспечить максимальные габариты для заданного радиуса резцовой головки. Известно, что угол ножки зуба колеса Θ f2 определяется выражением
tgθf2= 
 -
- 
(11) где lfn2 - ширина делительной впадины зуба колеса в нормальном сечении;
αn- угол исходного производящего контура;
ru - номинальный радиус резцовой головки или радиус кривизны продольной линии зуба колеса.
Приравняв выражение (11) нулю, получим
sin β2 = ru/R2 = rusin δ2 /r2. (12)
Это и есть условие получения равновысокого зуба.
В этом случае коэффициент увеличения размеров шестерни К не может выбираться произвольным образом, а должен определяться методом последовательных операций из системы одиннадцати трансцендентных уравнений (1-10) (12). После этого угол β1 наклона зуба шестерни может быть найден по известной методике (см. книгу К.М.Писманика "Гипоидные передачи").
Однако, выполненные исследования показали, что в предлагаемых передачах с углом β2 , определяемым зависимостью (12) с достаточной для практических расчетов точностью, принимая
cos η = 1, a cos( Σ-δ2 ) = cosδ1 разность μ углов наклона β1 и β2 определяется из выражения
sinμ= 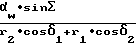

Таким образом, зная β2 из (12), угол β1 найдем по формуле
β1= β2 + arcsin(aw/R2), а из формул (6) и (7) получим, что начальный диаметр шестерни d1 связан с начальным диаметром колеса d2 соотношением
d1 = d2cos β2 /Ucos β1.
Устройство работает следующим образом.
При сборке гипоидной передачи с произвольно расположенными осями зубья шестерни 1 вводятся в зацепление с зубьями 6 колеса 2, передавая вращение с ведущего вала на ведомый путем взаимодействия зубьев колеса и шестерни, расположенных таким образом, что их начальные конусы касаются друг друга в точке Р, являющейся полюсом зацепления. Поскольку геометрические размеры сечения равновысокого зуба по длине не меняются, то его прочность на изгиб значительно выше этого же критерия для равнопонижающегося зуба и благодаря наличию продольного скольжения между зубьями передачи работает более плавно и предотвращает разрушение поверхностей зубьев от выкрашивания. Поскольку величина продольного скольжения невелика, то опасность заедания поверхностей зубьев таких гипоидных передач не выше, чем в передачах подобного рода (цилиндрических, конических). Увеличение геометрических параметров гипоидной передачи и применение равновысокого зуба в зацеплении значительно повышают ее нагрузочную способность.
Известно, что нагрузочная способность гипоидной передачи Т2 пропорциональна кубу ее линейных размеров
T R
R
Сравним для примера гипоидную передачу с равнопонижающимся зубом и гипоидную передачу с равновысоким зубом, нарезанные одной резцовой головкой с радиусом ru = 400 мм по нагрузочной способности.
Длина образующей начального конуса колеса R2 в гипоидной передаче с равнопонижающимся зубом равна
R2= r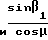 =400
=400  =228 мм с равновысоким зубом равна
=228 мм с равновысоким зубом равна
R2=  =
=  =761 мм
=761 мм
Коэффициент увеличения размеров шестерни К для гипоидной передачи с равнопонижающимся зубом составляет - 1,2, с равновысоким зубом составляет - 1,035.
Отношение нагрузочных способностей гипоидных передач с равнопонижающимся и равновысоким зубом Т2pn и T2pb соответственно составляет =
= =24 таким образом нагрузочная способность предложенной гипоидной передачи возрастает в 24 раза.
=24 таким образом нагрузочная способность предложенной гипоидной передачи возрастает в 24 раза.
Например, гипоидная передача с равновысоким зубом была рассчитана для планетарного стана винтовой прокатки Никопольского Южнотрубного завода.
При Z1 = 18, Z2 = 68, aw = 40 мм, Σ = 50о, r2 = 490, 196 мм получим передачу, где угол начального конуса колеса δ2 = 40о05'02"
угол начального конуса шестерни δ1 = =9о50'19".
Угол между проекцией общей нормали и осью колеса η = 2о59'32".
Угол между проекцией общей нормали и осью шестерни ε = 3o51'32".
Длина образующей начального конуса колеса R2 = 761,28 мм.
Длина образующей начального конуса шестерни R1 = 785,74 мм .
Угол спирали на колесе β2 = 31о39'17".
Угол спирали на шестерне β1 = =34о39'14".
Разность углов спирали шестерни и колеса μ = 2о59'58".
Нормальный модуль в средней точке зуба 12,273.
Расстояние от плоскости среднего диаметра колеса до линии кратчайшего межосевого расстояния С2 = 285,43 мм.
Расстояние от плоскости среднего диаметра шестерни до линии кратчайшего межосевого расстояния С1 = 750,97 мм.
Радиус резцовой головки ru = 400 мм.
Начальный диаметр шестерни d1 = =268,546 мм.
Предложенная гипоидная передача с произвольным расположением осей по сравнению с известными позволяет повысить надежность работы привода и уменьшить простои оборудования.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ НАРЕЗАНИЯ ЗУБЧАТЫХ КОЛЕС, ОБРАЗУЮЩИХ ГИПОИДНУЮ ПЕРЕДАЧУ | 1991 |
|
RU2043187C1 |
| СПОСОБ НАРЕЗАНИЯ КОНИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС | 1992 |
|
RU2041034C1 |
| Способ нарезания криволинейных зубьев гипоидных пар | 1991 |
|
SU1814598A3 |
| КОНИЧЕСКАЯ ГИПОИДНАЯ ЗУБЧАТАЯ ПЕРЕДАЧА СО СПИРАЛЬНЫМИ РАВНОВЫСОКИМИ ЗУБЬЯМИ | 1993 |
|
RU2074331C1 |
| АРОЧНАЯ ЗУБЧАТАЯ ПЕРЕДАЧА И СПОСОБ ЕЕ ИЗГОТОВЛЕНИЯ | 1995 |
|
RU2092725C1 |
| Способ коррекции формы круговых зубьев конических колес | 1990 |
|
SU1764871A1 |
| СПОСОБ НАРЕЗАНИЯ ЗУБЧАТЫХ КОЛЕС ГИПОИДНОЙ ПЕРЕДАЧИ | 1996 |
|
RU2111094C1 |
| СПОСОБ НАРЕЗАНИЯ КОНИЧЕСКИХ КОЛЕС | 1991 |
|
RU2043186C1 |
| СПОСОБ ИЗМЕРЕНИЯ ТРЕХМЕРНЫХ КООРДИНАТ | 1991 |
|
RU2015564C1 |
| ЭВОЛЬВЕНТНАЯ ЗУБЧАТАЯ КОРРИГИРОВАННАЯ ПЕРЕДАЧА ВНУТРЕННЕГО ЗАЦЕПЛЕНИЯ | 1991 |
|
RU2025614C1 |

Изобретение относится к машиностроению и может быть использовано для приводов планетарного стана винтовой прокатки. Гипоидная передача с произвольным расположением осей содержит конические шестерню и колесо с квазиэвольвентными зубьями. Зубья колеса выполнены равновысокими, а центр кривизны продольной линии зуба колеса расположен на полуокружности, диаметром которой служит образующая начального конуса, угол наклона зуба колеса в средней точки выполнен равным β2=arcsin(ru/R2) , где ru - радиус кривизны продольной линии зуба колеса, причем угол наклона зуба шестерни выполнен большим угла наклона зуба колеса на величину μ=arcsin(aw/R2) , где aw - гипоидное смешение. Начальный диаметр шестерни связан с начальным диаметром колеса приведенным соотношением. При сборке гипоидной передачи с произвольно расположенными осями зубья шестерни вводятся в зацепление с зубьями колеса, передавая вращение с ведущего вала на ведомый путем взаимодействия зубьев колеса и шестерни, расположенных таким образом, что их начальные конусы касаются друг друга в т.P, являющейся полюсом зацепления. 4 ил.
ГИПОИДНАЯ ПЕРЕДАЧА, содержащая конические шестерню и колесо с круговыми равновысокими зубьями, отличающаяся тем, что, с целью повышения ее нагрузочной способности, зубья колеса выполнены квазиэвольвентными, центр кривизны продольной линии зуба колеса расположен на окружности, радиусом которой служит образующая начального конуса, угол наклона зуба колеса в средней точке выполнен равным
β2 = arcsin(ru / R2) ,
где ru - радиус кривизны продольной линии зуба колеса,
причем угол наклона зуба шестерни выполнен большим угла наклона зуба колеса на величину
μ=arcsin(aw / R2) ,
где aw - гипоидное смешение;
R2 - длина образующей начального конуса колеса,
начальный диаметр шестерни связан с начальным диаметром колеса соотношением
d1 =  ,
,
где d2 - начальный диаметр колеса;
β2 - угол наклона зуба колеса;
β1 - угол наклона зуба шестерни;
U - передаточное число.
| Журавлев Г.А., Иофис Р.Б | |||
| Гипоидные передачи, проблемы и развитие, 1978, с.29-35. |
Авторы
Даты
1994-09-15—Публикация
1991-02-12—Подача