УСТРОЙСТВО ДЛЯ ОБРАБОТКИ МАТРИЦ Российский патент 1995 года по МПК G06F17/16 

Изобретение относится к вычислительной технике и микроэлектронике и может быть использовано в специализированных системах предварительной обработки многомерных сигналов.

Известно устройство для разложения Холецкого симметричной матрицы, содержащее первую матрицу из n запоминающих ячеек, вторую матрицу из (n 1) вычислительных ячеек и n-ю вычислительную ячейку [1]
Однако недостатком этого устройства являются ограниченные функциональные возможности в задачах предварительной обработки сигналов, не позволяющие выполнить с помощью данного устройства целый ряд алгоритмов, связанных с вычислением квадратичной формы.

Целью дополнительного изобретения является расширение функциональных возможностей устройства путем вычисления квадратичной формы.

Поставленная цель достигается тем, что известное устройство для предварительной обработки информации дополнительно содержит вторые информационные вход и выход, (n + 1)-ю вычислительную ячейку (ВЯ), содержащую вход, выход, умножитель и накапливающий сумматор, причем вход (n + 1)-й ВЯ соединен с вторым выходом (n-1)-й ВЯ и с первым и вторым входами умножителя, выход которого соединен с входом накапливающего сумматора, выход которого подключен к выходу (n + 1)-й ВЯ, выход (n + 1)-й ВЯ соединен с вторым информационным выходом устройства, n-я вычислительная ячейка дополнительно содержит третий вход, второй сумматор и второй, третий, четвертый и пятый мультиплексоры, причем третий вход этой же ВЯ соединен с вторым информационным входом и первым входом второго сумматора, выход которого подключен к первому входу четвертого мультиплексора, второй вход второго сумматора соединен с выходом блока изменения знака, первый вход второго мультиплексора соединен с первым входом этой же ВЯ, второй вход пятого мультиплексора соединен с выходом умножителя, первый вход третьего мультиплексора соединен с выходом блока вычисления обратной величины, причем выход блока вычисления квадратного корня подключается к входу блока вычисления обратной величины через второй вход второго мультиплексора, выход блока вычисления обратной величины подключается к входу первого регистра через первый вход пятого мультиплексора, второй вход этой же ВЯ подключается к первому входу умножителя через второй вход четвертого мультиплексора, выход блока изменения знака подключается к второму входу умножителя через второй вход третьего мультиплексора, j-я вычислительная ячейка (j 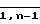) вместо второго и третьего мультиплексора 2 х 1 содержит мультиплексоры 3 х 1, причем третьи входы второго и третьего мультиплексоров подключены соответственно к четвертому входу сумматора.

На фиг. 1 представлена функциональная схема предлагаемого устройства; на фиг. 2 функциональная схема n-ой вычислительной ячейки; на фиг. 3 функциональная схема j-й вычислительной ячейки (j 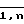); на фиг. 4 функциональная схема (n + 1)-й вычислительной ячейки; на фиг. 5 организация потоков информации в вычислительных ячейках; на фиг. 6 временная диаграмма работы вычислительных ячеек.

Устройство (фиг. 1) для предварительной обработки информации содержит два информационных входа 1.1 и 1.2, матрицу 2 из n запоминающих ячеек (ЗЯ) 3, два информационных выхода 4.1 и 4.2, n-ю ВЯ 5, матрицу 6 из (n 1) ВЯ 7, (n + 1)-ю ВЯ 27, причем первые вход и выход j-й (j 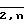) ЗЯ 3 соединены с первыми выходом и входом соответственно (j 1)-й ВЯ 7, а первые вход и выход первой ЗЯ 3 соединены соответственно с первыми выходом и входом n-й ВЯ 5, второй выход j-й (j 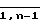) ЗЯ 3 подключен к второму входу (j + 1)-й ЗЯ 3, второй выход n-й ЗЯ 3 является первым информационным выходом 4.1 устройства, второй вход первой ЗЯ 3 является первым информационным входом 1.1 устройства, третий вход n-й ВЯ 5 является вторым информационным входом 1.2 устройства, выход (n + 1)-й ВЯ 27 является вторым информационным выходом 4.2 устройства, второй и третий выходы j-й (j 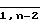) ВЯ 7 подключены соответственно к второму и третьему входам (j + 1)-й ВЯ 7, а второй и третий выходы n-й ВЯ 5 подключены к второму и третьему входам первой ВЯ 7; четвертый вход j-й (j 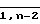) ВЯ 7 соединен с четвертым выходом (j + 1)-й ВЯ 7, четвертый выход первой ВЯ 7 подключен к второму входу n-й ВЯ 5, второй выход (n 1)-й ВЯ 7 подключен к входу (n + 1)-й ВЯ 27.

Вычислительная ячейка 5 с номероом n содержит (фиг. 2) первый вход 5.1, первый выход 5.2, третий выход 5.3, второй вход 5.4, третий вход 5.6, регистр 8, блок вычисления квадратного корня 9, мультиплексор 10, блок вычисления обратной величины 11, первый сумматор 12, регистр 13, умножитель 14, блок изменения знака числа 15, регистр 16, второй сумматор 28, мультиплексоры 29-32, причем вход 5.1 соединен с первыми входами сумматора 12, мультиплексора 29 и входом блока 9 вычисления квадратного корня, выход которого соединен с вторым входом мультиплексора 29 и первым входом мультиплексора 10; выход мультиплексора 29 соединен с входом блока 11 вычисления обратной величины, выход которого соединен с первым входом мультиплексора 30 и первым входом мультиплексора 32, второй вход которого подключен к выходу умножителя 14, а выход мультиплексора 32 соединен с входом регистра 13, выход которого является выходом 5.5 n-й ВЯ 5; второй вход мультиплексора 10 подключен к выходу сумматора 12, а выход мультиплексора 10 соединен с входом регистра 8, выход которого является выходом 5.2 n-й ВЯ 5; второй вход сумматора 12 соединен с выходом умножителя 14, первый вход которого соединен с выходом мультиплексора 31, а второй вход умножителя 14 соединен с выходом мультиплексора 30; третий вход 5.6 n-й ВЯ 5 соединен с первым входом мультиплексора 30 и первым входом сумматора 28, выход которого подключен к первому входу мультиплексора 31; второй вход мультиплексора 31 объединен с входом блока 15 изменения знака числа и является входом 5.4 n-й ВЯ 5; выход блока 15 изменения знака числа соединен с вторыми входами мультиплексора 30, сумматора 28 и входом регистра 16, выход которого является выходом 5.3 n-й ВЯ 5.

Вычислительная ячейка 7 с номером j (j 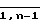) содержит (фиг. 3) третий вход 7.1, первый вход 7.2, первый выход 7.3, третий выход 7.4, четвертый вход 7.5, второй выход 7.6, второй вход 7.7, четвертый выход 7.8, мультиплексоры 17-19, умножитель 20, сумматор 21, регистры 22-25 и мультиплексор 26, причем вход 7.2 подключен к первым входам мультиплексоров 17-18, выходы которых соединены соответственно с первыми входами умножителя 20 и сумматора 21; второй вход мультиплексора 17 объединен с третьим входом мультиплексора 18, вторым входом мультиплексора 26 и является входом 7.5 ВЯ 7, а второй вход мультиплексора 18 соединен с входом константы "0"; первый вход мультиплексора 26 подключен к выходу умножителя 20 и второму входу сумматора 27, выход которого соединен с входом регистра 22 и третьим входом мультиплексора 26, выход регистра 22 является выходом 7.3 ВЯ 7; выход мультиплексора 26 соединен с входом регистра 25, выход которого является выходом 7.8 ВЯ 7; второй вход умножителя 20 подключен к выходу мультиплексора 19, первый вход которого объединен с входом регистра 23 и является входом 7.7 ВЯ 7, а второй вход мультиплексора 19 объединен с входом регистра 24 и является входом 7.1 ВЯ 7; выход регистров 23-24 являются соответственно выходами 7.6 и 7.4 ВЯ 7.

Вычислительная ячейка 27 с номером (n + 1) (фиг. 4) содержит вход 27.1, выход 27.2, умножитель 33 и накапливающий сумматор 34, причем вход ВЯ 27.1 соединен с первым и вторым входами умножителя 33, выход которого соединен с входом накапливающего сумматора 34; выход накапливающего сумматора 34 соединен с выходом ВЯ 27.2 и является вторым информационным выходом устройства 4.2.

Устройство работает следующим образом.

Квадратичной форму можно записать в следующем виде
Ψ= Х^т ˙ А^-1˙Х, (1) где Т значок, обозначающий транспортирование;
А^-1 матрица, обратная матрице А; при условии задании матрицы А (порядка n) и вектора Х размером n * 1.

Одна из возможных стратегий нахождения согласно (1) представлена в таблице.

Нахождение разложения матрицы А на множители (2) осуществляется аналогичным образом как в устройстве прототипа [1] за исключением того, что вычисленные элементы матрицы 1, не выводятся из запоминающих ячеек 3 и используются на втором шаге вычисления (таблица).

Рассмотрим второй и третий шаги вычислений.

Раскрывая (3), запишем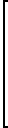

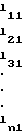
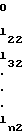
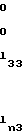
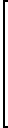
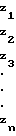
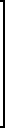
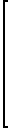
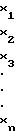
(5)
Система вида (3) и (5) решается методом прямой подстановки следующим образом:
Пусть ∀i ∈ 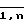y_i,o= 0 тогда
Z₁ (X₁ Y_1,0)/l₁₁.

Далее, для каждого i ∈ 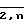вычислим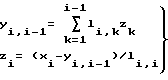

(6) что и дает решение системы линейных алгебраических уравнений (СЛАУ).

Выражение со знаком суммы в представленном алгоритме (6) заменим рекуррентным выражением, связывающим вычисляемое значения y_i,i-1 с номером такта и номером ячейки, в которой это значение вычисляется. В результате этого можно записать
Пусть ∀i ∈ 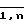y_i,o= 0 тогда
z₁ (x₁ y_1,0)/l_11.
Далее, для каждого i ∈ 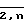определим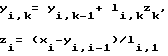

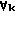
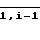
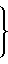
(7) При этом n-я ВЯ 5 должна выполнять следующие функции:
z_вых (x_вх y_вх)/l_вх (8)
только для нечетных микротактов.

ВЯ 7 реализуют функции вида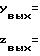

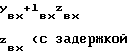
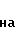
(9)
для всех микротактов, кратных номеру i ВЯ 7.

Входы ВЯ 5 и ВЯ 7 5.1 и 7.1 соответственно предназначены для приема элементов матрицы L при их считывании по диагонали (фиг. 5); вход 5.6 ВЯ 5 для приема элементов вектора Х; входы 5.4 ВЯ 5 и 7.5 ВЯ 7 для приема y_вх; входы 7.7 ВЯ 7 для приема z_вх; входы 5.5 ВЯ 5 и 7.6 ВЯ 7 для выдачи z_вых, входы 7.8 ВЯ 7 для выдачи y_вых.
Треугольная СЛАУ в устройстве решается за один макротакт в течение (3n 2) микротактов.

Временная диаграмма, поясняющая организацию потоков данных в вычислительных ячейках для случая n 4, приведена на фиг. 6.

На третьем шаге вычисления в устройстве реализуется вычисление произведения матрицы-строки на матрицу-столбец. Выражение (4) можно записать в следующем виде
Ψ Z^тZ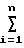z3i

Вычисление согласно (10) реализуется в (n + 1) ВЯ 27 с помощью умножителя 33 и накапливающего сумматора 34. Элементы z_i поступают на вход умножителя 33 со входа 27.1, а результат вычислений поступает с выхода накапливающего сумматора 34 на выход ВЯ 27 27.2 и далее на второй информационный выход устройства 4.2. Результат на выходе устройства появится через один микротакт, после того как была решена в устройстве треугольная СЛАУ на втором шаге вычисления.

Таким образом, выполняя последовательно в предлагаемом устройстве три вычислительные процедуры: разложение матрицы по методу Холецкого, решение треугольной СЛАУ и произведение матрицы-строки на матрицу-столбец, достигается цель расширения функциональных возможностей за счет решения задачи нахождения квадратичной формы.

Предлагаемое изобретение позволяет достичь следующих технико-экономических преимуществ:
решить новый класс задач, связанных с решением СЛАУ и вычислением квадратичной формы;
линейная структура вычислительных ячеек позволяет реализовать предлагаемое устройство на современной элементной базе.

В организации-заявителе было проведено моделирование на ППЭВМ типа IBM PC/AT предлагаемого устройства с учетом аппаратной реализации и создан макет устройства, реализованного с использованием ИМС микропроцессорного комплекта 1843.

Изобретение относится к вычислительной технике и микроэлектронике и может быть использовано в специализированных системах предварительной обработки многомерных сигналов. Цель - расширение функциональных возможностей за счет вычисления квадратичной формы. Цель достигается тем, что в устройство, содержащее первую матрицу из n-запоминающих ячеек, вторую матрицу из (n - 1) вычислительных ячеек, n-ю вычислительную ячейку, введена дополнительная (n + 1)-я вычислительная ячейка, позволяющая выполнять операции: возведение в квадрат и суммирование с накоплением; а также n-я вычислительная ячейка дополнительно содержит сумматор и четыре мультиплексора. 2 з.п. ф-лы, 6 ил.

1. УСТРОЙСТВО ДЛЯ ОБРАБОТКИ МАТРИЦ, содержащее группу памятей, соединенных двусторонними связями с соответствующими блоками обработки группы и с первым дополнительным блоком обработки, соединенным двусторонними связями с первым блоком обработки группы, каждый блок обработки группы соединен двусторонними связями с предыдущим и последующим блоками обработки группы, вход первой памяти и выход последней памяти группы являются входом и выходом устройства, выход предыдущей памяти группы соединен с входом последующей памяти группы, отличающееся тем, что в устройство введен второй дополнительный блок обработки, причем вход первого дополнительного блока обработки является входом устройства, выход которого соединен с выходом второго дополнительного блока обработки, вход которого соединен с выходом последнего блока обработки группы. 2. Устройство по п.1, отличающееся тем, что второй дополнительный блок обработки содержит соединенные последовательно квадратор и сумматор, вход квадратора и выход сумматора являются входом и выходом блока. 3. Устройство по п.1, отличающееся тем, что первый дополнительный блок обработки содержит три регистра, пять мультиплексоров, два сумматора, узел извлечения корня, формирователь обратной величины, умножитель, формирователь знака числа, причем выход узла извлечения корня соединен с входами первого и второго мультиплексоров, выход первого мультиплексора через формирователь обратной величины соединен с входами третьего и четвертого мультиплексоров, выход третьего мультиплексора соединен с входом первого регистра, выход формирователя знака числа соединен с входами второго регистра, четвертого мультиплексора и первого сумматора, выход которого соединен с входом пятого мультиплексора, выходы которого и четвертого мультиплексора через умножитель соединены с входами третьего мультиплексора и второго сумматора, выход которого через второй мультиплексор соединен с входом третьего регистра, выходы с первого по третий регистров являются выходами блока, входы первого сумматора, формирователя знака числа и пятого мультиплексора, первого мультиплексора, второго сумматора и узла извлечения корня соединены с входами блока.