Изобретение относится к способам измерения параметров сигналов РНС длинноволнового диапазона на фоне интерферирующих отражений от ионосферы и флюктуационных помех и может быть использовано для повышения точности определения местоположения подвижного объекта, находящегося в рабочей зоне РНС.
Целью изобретения является повышение точности определения радионавигационного параметра.
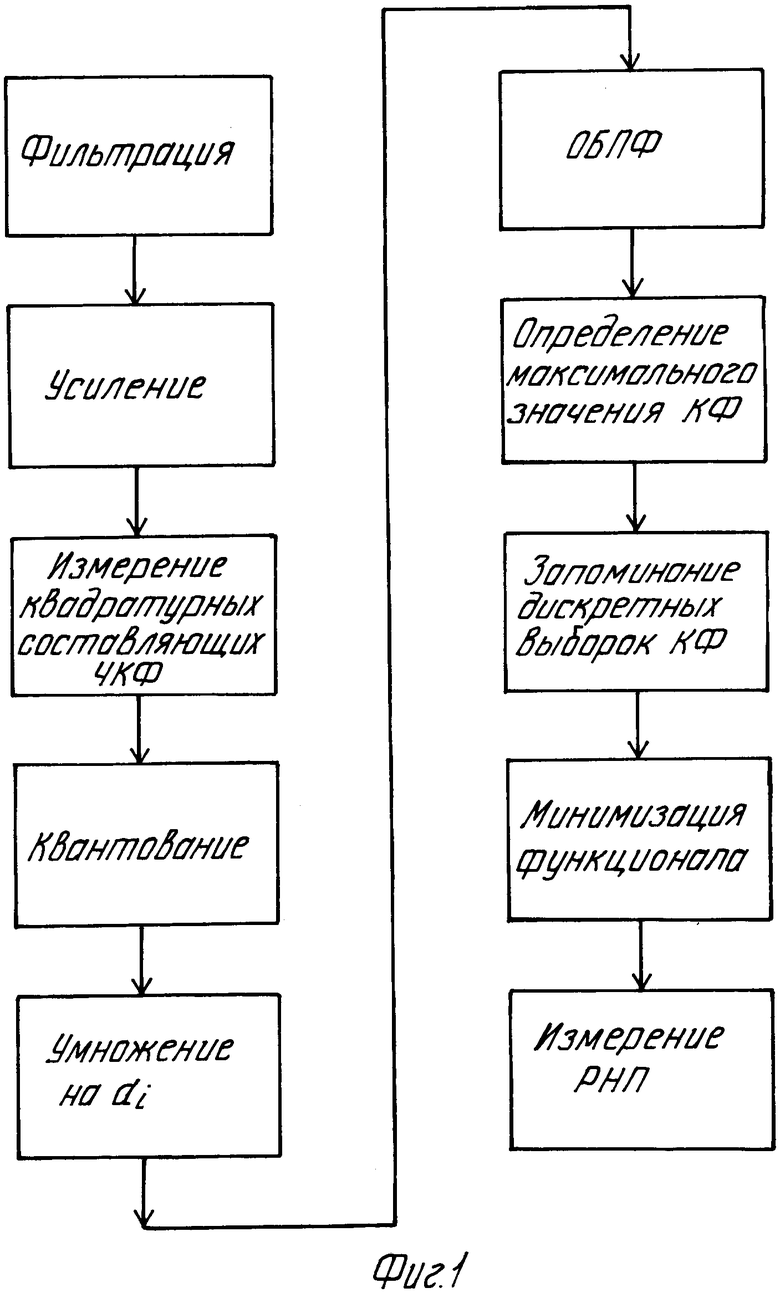
На фиг. 1 представлена последовательность выполняемых над принятым сигналом действий; на фиг. 2 структурная электрическая схема устройства, реализующего способ.
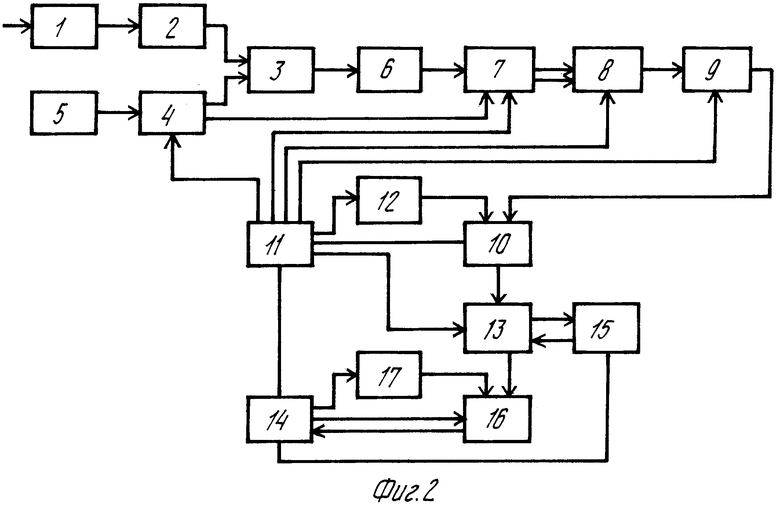
Устройство, реализующее способ, содержит антенный блок 1, усилитель 2 высокой частоты, смеситель 3, блок 4 гетеродинных частот, опорный генератор 5, усилитель 6 промежуточной частоты, квадратурный коррелятор 7, переключатель 8, аналого-цифровой преобразователь 9, арифметическо-логические устройства 10, 16, блоки управления 11, 14, постоянные запоминающие устройства 12, 17, оперативное запоминающее устройство 13, процессор 15 обратного преобразования Фурье.
Сущность способа заключается в следующем.
Сигнал РНС может быть представлен в виде последовательности частотных элементов (импульсов), несущие частоты которых отличаются на величину частотного интервала, кратного частоте Fn. Сложный многочастотный (СМЧ) сигнал может быть записан в следующем виде: (
(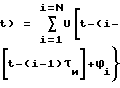 1)
1)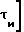 cos
cos  2πf1+(i-1)2πF
2πf1+(i-1)2πF × (1) где U(t) амплитуда элемента сигнала,
× (1) где U(t) амплитуда элемента сигнала,
u(t) 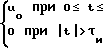
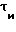 (2) f1 нижняя частота спектра СМЧ-сигнала,
(2) f1 нижняя частота спектра СМЧ-сигнала,
Fn величина частотного интервала,
N число элементов СМЧ-сигнала,
τи длительность элемента сигнала.
Ширина спектра СМЧ-сигнала определяется величиной
Δ Fсп f1 + (N 1) Fn (3)
Общая длительность СМЧ-сигнала составит величину:
Tc N τи. (4)
Ввиду того что излучение коротких по длительности импульсных сигналов в длинноволновой радионавигации затруднительно, СМЧ-сигнал в этом диапазоне частот формируют за счет временной избыточности, т.е. за счет излучения элементов большой длительности (десятки мс).
Таким образом, спектр каждого элемента СМЧ-сигнала (Δ F1) является узкополосным (десятки Гц):
Δ F1 << Δ Fсп (5)
Обработка принимаемого СМЧ-сигнала осуществляется корреляционным методом. При этом сначала вычисляются значения взаимно корреляционных функций между каждым элементом СМЧ-сигнала и аналогичным ему элементом опорного сигнала, называемые далее частными корреляционными функциями (ЧКФ).
С точностью до постоянного множителя квадратурные составляющие ЧКФ, вычисляемые с помощью двухканального коррелятора, имеют вид
ϑis Ui sin ωi τ, (6)
ϑic Ui cos ωi τ, (7) где Ui амплитуда i-го элемента СМЧ-сигнала;
ωi его частота.
Квадратурные составляющие корреляционной функции СМЧ-сигнала, называемой далее корреляционной функцией (КФ), имеют вид
Ψc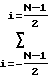 cosi2πFп·τ·sinωoτ (8)
cosi2πFп·τ·sinωoτ (8)
Ψc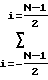 cosi2πFп·τ·cosωoτ (9) где ωо центральная частота спектра сигнала.
cosi2πFп·τ·cosωoτ (9) где ωо центральная частота спектра сигнала.
Квадратурные составляющие КФ СМЧ-сигнала, как следует из приведенных выражений, являются периодическими функциями с периодом повторения Tn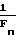 имеют импульсную структуру с огибающей ΨE
имеют импульсную структуру с огибающей ΨE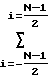 cosi2πFпτ и высокочастотным заполнением с частотой ωо.
cosi2πFпτ и высокочастотным заполнением с частотой ωо.
Ширина основного пика КФ ( τс) определяется шириной спектра СМЧ-сигнала Δ Fсп и поэтому τс < τи, т.е. длительность основного пика много меньше длительности элемента сигнала.
Аналогичную структуру имеет КФ отраженных от ионосферы сигналов, с той лишь разницей, что пространственный сигнал задержан относительно поверхностного сигнала на величину Δ τ и имеет произвольную амплитуду и фазу.
Огибающая КФ СМЧ-сигнала, представленная выше, имеет значительный уровень боковых лепестков, которые в условиях интерференции поверхностного и пространственного сигналов осложняют селекцию сигналов и снижают точность измерения радионавигационного параметра (РНП). Под РНП в дальнейшем будем понимать временное положение поверхностного сигнала, измеренное по его корреляционной функции с точностью до фазы ее высокочастотного заполнения относительно некоторой фазы (времени) опорного сигнала (квазидальность).
С целью уменьшения влияния боковых лепестков КФ на точность измерения параметра осуществляется взвешивание элементов сигнала путем умножения квадратурных составляющих ЧКФ на весовые множители ai. Это, с одной стороны, позволяет реализовать требуемый вид корреляционной функции СМЧ-сигнала, который является наиболее оптимальным для рассматриваемой процедуры обработки сигнала, с другой стороны, приводит к определенным энергетическим потерям, поскольку при оптимальной обработке принимаемого сигнала ai 1. Однако величина этих потерь, как показывают расчеты и эксперимент, составляет не более 8-10% С учетом весовой обработки квадратурные составляющие ЧКФ i-го элемента имеют вид
ϑis ai Ui sin ωi τ, (10)
ϑic ai Ui cos ωi τ, (11)
Ввиду того что частотные элементы СМЧ-сигнала по существу представляют собой набор гармонических составляющих спектра сигнала, то измеренные значения ЧКФ пропорциональны амплитуде этих гармонических составляющих, и, выполняя Фурье-преобразование над взвешенными значениями ЧКФ, можно перейти от обработки спектральных составляющих СМЧ-сигнала к обработке временных выборок КФ-сигнала, взятых в дискретных точках периода ее повторения. Предлагаемый поиск максимума КФ принятой смеси сигналов позволяет определить на периоде ее повторения область возможного нахождения КФ поверхностного сигнала. Действительно, если отношение пространственного и поверхностного сигналов (γ) меньше 1, то положение максимума КФ поверхностного сигнала будет незначительно отличаться от временного положения максимума КФ принимаемой смеси сигналов. Если же γ > 1, то положение максимума КФ принятой смеси в основном будет определяться положением максимума КФ однократно отраженного от ионосферы сигнала (отражение более высокого порядка кратности (m) меньше по амплитуде первого отражения и задержаны по времени на величину Δ τm). В этом случае выборки, соответствующие КФ поверхностного сигнала, будут предшествовать положению максимума, т.е. расположены слева от него (так как отраженный сигнал всегда запаздывает). Поэтому в предлагаемом способе используются в обработке только те дискретные функции корреляции принятой смеси сигналов, которые расположены в окрестности найденного максимума, причем количество дискретных выборок справа от найденного максимума должно определяться минимальной величиной задержки однократно отраженного от ионосферы сигнала, а слева от него максимальной величиной задержки, при которой γ > 1. Эти данные априорно могут быть известны с учетом рассматриваемых расстояний от наземных станций РНС.
Указанное обстоятельство позволяет значительно упростить ожидаемую модель принимаемого сигнала, что обеспечивает практическую реализацию предлагаемого технического решения, и исключить влияние m-кратных отражений на точность измерения РНП. Обозначим через Апсs ожидаемое значение амплитуды одной из квадратурных составляющих корреляционной функции поверхностного сигнала, а через Впрs ожидаемое значение амплитуды одной из квадратурных составляющих КФ пространственного сигнала. Тогда за оценки этих параметров принимают такие числовые значения, которые минимизируют величину функционала L:
L 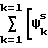 -A
-A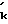 -B
-B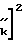 (12) где ϑks(ϑkc) k-й вычисленный отсчет квадратурной (синусной, косинусной) составляющей корреляционной функции принимаемого сигнала;
(12) где ϑks(ϑkc) k-й вычисленный отсчет квадратурной (синусной, косинусной) составляющей корреляционной функции принимаемого сигнала;
Апсs(Апсс) ожидаемое значение амплитуды квадратурной составляющей корреляционной функции поверхностного сигнала;
Впрs(Впрс) ожидаемое значение амплитуды квадратурной составляющей корреляционной функции пространственного сигнала;
Rk' k-е значение нормированной огибающей суммарной корреляционной функции поверхностного сигнала;
Rk''- k-е значение нормированной огибающей суммарной корреляционной функции пространственного сигнала;
l число дискретных отсчетов.
Рассматривая L как функцию неизвестных параметров Апсs и Впрs, находим искомые оценки этих параметров, решая систему линейных уравнений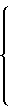
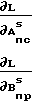

 (13)
(13)
Подставляя решение системы уравнений (13) в выражение (12) и производя несложные алгебраические преобразования, получают
Z 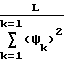 1
1 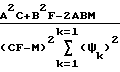 (14) где A
(14) где A 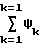 R
R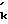 , B
, B 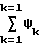 R
R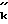
C 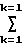 (R
(R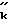 )2, F
)2, F 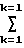 (R
(R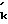 )2, M
)2, M 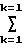 R
R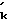 R
R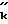 Поиск минимума по ансамблю рассматриваемых моделей сигнала (каждая модель соответствует определенному набору массивовRk'} иRk''} определяющих гипотезу о положении максимума КФ поверхностного и пространственного сигналов) совпадает с поиском максимума функции
Поиск минимума по ансамблю рассматриваемых моделей сигнала (каждая модель соответствует определенному набору массивовRk'} иRk''} определяющих гипотезу о положении максимума КФ поверхностного и пространственного сигналов) совпадает с поиском максимума функции
Q1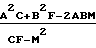
Производя аналогичные вычисления с использованием дискретных выборок другой квадратурной составляющей КФ принимаемого сигнала, вычисляют значение Q2. Фиксируя максимум функции
Q Q1 + Q2 (17) при выбранных наборах массивовRk'} иRk''} определяют временное положение интерферирующих сигналов по положению максимумов рассматриваемых моделей. Поиск моделей, минимизирующих функционал L, может осуществляться, например, с использованием метода "золотого" сечения (Д. Химмельблад. Прикладное нелинейное программирование. М. изд-во "Мир", 1975, стр. 50).
В результате предлагаемых действий над принятым СМЧ-сигналом определяют следующие параметры: τпс временное положение максимума огибающей КФ поверхностного сигнала; ϕпс фаза поверхностного сигнала, вычисляемая как
ϕпс= arctg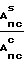 (18) Вычисление значений Апсs и Апсc, соответствующих минимуму функционала L, осуществляют по формуле (с использованием дискретных выборок квадратурных составляющих КФ принимаемого сигнала)
(18) Вычисление значений Апсs и Апсc, соответствующих минимуму функционала L, осуществляют по формуле (с использованием дискретных выборок квадратурных составляющих КФ принимаемого сигнала)
Aпс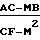 (19) С учетом введенных обозначений способ измерения радионавигационного параметра заключается в следующем.
(19) С учетом введенных обозначений способ измерения радионавигационного параметра заключается в следующем.
Принимаемый СМЧ-сигнал предварительно фильтруется в полосе приемного устройства, усиливается и поступают на двухканальный коррелятор, в котором вычисляются квадратурные составляющие взаимно корреляционных функций (частных корреляционных функций) каждого элемента многочастотного сигнала с аналогичным ему элементом опорного сигнала. Далее вычисленные значения квантуются. Квантовые значения квадратурных составляющих ЧКФ умножаются на весовые множители ai и подвергаются обратному преобразованию Фурье (ОБПФ) с целью вычисления значений квадратурных составляющих корреляционной функции СМЧ-сигнала на периоде ее повторения. По дискретным значениям огибающей КФ определяется временное положение максимума КФ принятой смеси сигналов. В окрестности максимума запоминаются ряд дискретных выборок КФ с шагом дискретизации, кратным периоду средней частоты спектра СМЧ-сигнала.
Выбранные в окрестности максимума дискретные выборки КФ сравнивают с дискретными выборками ожидаемой модели сигнала, представляющей собой суперпозицию корреляционных функций поверхностного и пространственного сигналов.
Рассматривая различные гипотезы о положении максимумов КФ интерферирующих сигналов, фиксируют положение моделей, дающее минимальное среднеквадратическое отклонение от КФ принимаемого сигнала. По найденным оценкам парамет- ров Апсs; Апсc;Rk'} измеряют радионавигационный параметр (РНП), используя грубый отсчет по огибающей КФ поверхностного сигнала и фазу ее высокочастотного заполнения (квазидальность).
Устройство для осуществления способа измерения РНП работает следующим образом.
Принимаемый СМЧ-сигнал с выхода антенного блока 1 подается на усилитель 2 высокой частоты, где усиливается и с выхода усилителя поступает на один из входов смесителя 3. На второй вход смесителя подается опорный сигнал, аналогичный по своему формату принимаемому сигналу и формируемый в блоке 4 гетеродинных частот. Несущие частоты элементов опорного сигнала отличаются от частот элементов принимаемого сигнала на величину fпр. Вход блока 4 гетеродинных частот подключен к выходу опорного (задающего) генератора 5.
С выхода смесителя 3 частотные элементы сигнала с несущей частотой fпр подаются на вход усилителя 6 промежуточной частоты, с выхода которого сигнал подается на квадратурный (двухканальный) коррелятор 7, на другой вход которого подается опорный сигнал со второго выхода блока 4 гетеродинных частот. Переключатель 8 поочередно подключает к выходам квадратурного коррелятора 7 аналого-цифровой преобразователь 9. Квантованные значения квадратурных составляющих ЧКФ поступают на вход арифметическо-логического устройства (АЛУ) 10. По адресам, задаваемым блоком управления 11 из постоянного запоминающего устройства 12 производится выборка весовых коэффициентов спектра, подаваемых на второй вход АЛУ 10. На третий вход АЛУ 10 от БУ 11 подаются последовательности команд (кодов), определяющие загрузку значений ЧКФ, весовых коэффициентов, перемножение их и выгрузку взвешенных значений квадратурных составляющих ЧКФ в оперативном запоминающем устройстве (ОЗУ) 13 по адресам, задаваемым БУ 11.
По сигналу синхронизации блока управления 14 запускается процессор 15, который преобразует взвешенные значения квадратурных составляющих ЧКФ в дискретные отсчеты корреляционной функции СМЧ-сигнала, записывая их в ОЗУ 13. По адресам, вырабатываемым БУ 11 под управлением БУ 14, АЛУ 16 производит последовательный выбор дискретных выборок квадратурных составляющих корреляционной функции СМЧ-сигнала с одновременным поиском максимального значения огибающей корреляционной функции, адрес которого передается в БУ 14. БУ 14 последовательно определяет посредством БУ 11 адреса обрабатываемых отсчетов корреляционной функции, записанных в ОЗУ 13, адреса отсчетов модели сигнала, записанной в ПЗУ 17, и команды (коды), определяющие последовательность операций, выполняемых АЛУ 16, необходимых для минимизации функционала. Определенные в результате минимизации оценки параметров Апсs, Апсс и τпс используются для определения РНП. Кроме того БУ 11 генерирует соответствующие каждому моменту времени коды управления для перестройки блока гетеродинных частот, управления квадратурным коррелятором, переключателем и АЦП.
| название | год | авторы | номер документа |
|---|---|---|---|
| ПРИЕМОИНДИКАТОР СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ | 1993 |
|
RU2067771C1 |
| ПРИЕМНИК СИГНАЛОВ СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ | 1993 |
|
RU2110149C1 |
| УСТРОЙСТВО ДЛЯ ПРИЕМА СИГНАЛОВ СТАНЦИИ ИМПУЛЬСНО-ФАЗОВОЙ РАДИОНАВИГАЦИОННОЙ СИСТЕМЫ | 1991 |
|
RU2014629C1 |
| СВЧ-ПРИЕМНИК СИГНАЛОВ СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ | 1993 |
|
RU2097919C1 |
| СПОСОБ УГЛОВОЙ ОРИЕНТАЦИИ ОБЪЕКТА ПО РАДИОНАВИГАЦИОННЫМ СИГНАЛАМ КОСМИЧЕСКИХ АППАРАТОВ | 2016 |
|
RU2618520C1 |
| УСТРОЙСТВО ДЛЯ ПРИЕМА СИГНАЛОВ СТАНЦИИ ИМПУЛЬСНО-ФАЗОВОЙ РАДИОНАВИГАЦИОННОЙ СИСТЕМЫ | 1991 |
|
RU2014630C1 |
| СПОСОБ ИЗМЕРЕНИЯ ЗАДЕРЖКИ РАДИОИМПУЛЬСА ОТНОСИТЕЛЬНО МЕСТНОГО ОПОРНОГО СИГНАЛА | 1991 |
|
RU2012026C1 |
| ДАЛЬНОМЕРНЫЙ СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ И СОСТАВЛЯЮЩИХ ВЕКТОРА СКОРОСТИ ОБЪЕКТОВ ПО РАДИОСИГНАЛАМ КОСМИЧЕСКИХ АППАРАТОВ СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ | 1994 |
|
RU2115137C1 |
| СПОСОБ ИЗМЕРЕНИЯ ВЫСОТЫ И УСТРОЙСТВО РАДИОВЫСОТОМЕРА С НЕПРЕРЫВНЫМ ЛЧМ СИГНАЛОМ, ИСПОЛЬЗУЮЩЕГО СПОСОБ | 2013 |
|
RU2550082C1 |
| СПОСОБ РАДИОКОНТРОЛЯ | 2004 |
|
RU2287169C2 |
Использование: измерение параметров сигналов радионавигационных систем длинноволнового диапазона на фоне интерферирующих отражений от ионосферы и флюктуационных помех. Сущность изобретения заключается в осуществлении обратного Фурье преобразования над взвешенными значениями квадратурных составляющих взаимно-корреляционных функций элементов сложного многочастотного сигнала, в результате чего вычисляются дискретные значения квадратурных составляющих корреляционной функции сложного многочастотного сигнала. Определяется временное положение максимума огибающей этой корреляционной функции. В окрестности максимума выбирается ряд дискретных выборок квадратурных составляющих корреляционной функции с интервалом, кратным периоду многочастотного сигнала. Число этих выборок определяется ожидаемой величиной задержки однократно отраженного от моносферы сигнала. Выбранные таким образом отсчеты сравниваются с дискретными выборками ожидаемой модели сигнала. Рассматривая различные гипотезы о временном положении модели, представляющей собой суперпозицию поверхностного и однократно отраженного от ионосферы сигнала, вычисляются оценки параметров модели, дающей минимальное среднеквадратическое отклонение от корреляционной функции принимаемой смеси сигналов. По измеренным оценкам определяется радионавигационный параметр. 2 ил.
СПОСОБ ОПРЕДЕЛЕНИЯ РАДИОНАВИГАЦИОННОГО ПАРАМЕТРА СИГНАЛОВ ИМПУЛЬСНО-ФАЗОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ, принимаемых на фоне пространственных сигналов, включающий прием излучаемого сигнала, определение дискретных значений квадратурных составляющих взаимно корреляционной функции принятого поверхностного и опорного сигналов, свободной от пространственных сигналов, отличающийся тем, что, с целью повышения точности определения радионавигационного параметра, определяют временное положение максимума взаимно коррекляционной функции принятого и опорного сигналов, дополнительно определяют в его окрестностях дискретные значения Ψ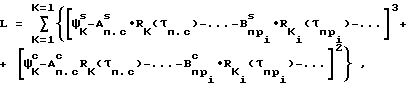
где 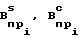 оценки амплитуд квадратурных составляющих взаимно корреляционной функции i-х пространственного и опорного сигналов;
оценки амплитуд квадратурных составляющих взаимно корреляционной функции i-х пространственного и опорного сигналов;
RК(τп.с) K-е значение нормированной огибающей взаимно корреляционной функции поверхностного и опорного сигналов, максимум которой находится в точке τп.с;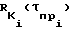 K-е значение нормированной огибающей взаимно корреляционной функции i-пространственного и опорного сигналов, максимум которой находится в точке
K-е значение нормированной огибающей взаимно корреляционной функции i-пространственного и опорного сигналов, максимум которой находится в точке 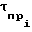 ;
;
l число дискретных отсчетов.
| Лутченко А.Е | |||
| Когерентный прием радионавигационных сигналов | |||
| М.: "Сов.радио", 1973, с.161-162. |
Авторы
Даты
1995-07-25—Публикация
1986-08-04—Подача