Изобретение относится к способам определения молекулярно-массового распределения как линейных полимеров, так и межузловых цепей сетчатых полимеров.
Известен способ определения молекуляорно-массового распределения (ММР) линейных полимеров и межузловых цепей сетчатых полимеров, основанный на анализе зависимости податливости полимерного образца от температуры в условиях сканирования по температуре с постоянной скоростью в диапазоне температур от температуры стеклования полимера до температуры полного перехода полимера в высокоэластическое или вязкотекучее состояние. Измерение податливости произоводится с помощью полусферического пуансона. Согласно известному способу, глубина погружения полусферического пуансона при постоянной нагрузке пропорциональна объемной доле тех полимерных цепей, чья длина не превышает длины плавящихся при данной температуре цепей. Так как полимеры с различными длинами цепей плавятся при разных температурах, сканированием по температуре получают развертку объемной доли полимера по длинам цепей.
Недостатком известного способа является неточное определение формы зависимости податливости от длины "расплавленных" цепей. Данная зависимость была определена авторами известного способа экспериментально, что в условиях отсутствия надежных методов полимеров с заданной длиной цепи привело к источнику показателя степени в зависимости модуля Юнга от объемной доли "расплавленного" полимера (т. е. от объемной доли макромолекул, чьи цепи короче плавящихся при данной температуре). Для полусферического пуансона модуль Юнга E обратно пропорционален смещению пуансона в степени полтора:
E ≈ 1/(1)3/2
Это для известного способа дает обратную пропорциональность модуля Юнга объемной доле "расплавленных" цепей в степени полтора: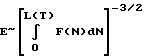
где E - модуль Юнга, F(N) - весовая функция молекулярно-массового распределения полимера по количеству N звеньев в цепи, L(T) - длина цепи полимера, плавящегося при температуре T: цепи короче, чем L(T) "расплавлены" (сравнительно свободно двигаются в объеме полимера), цепи длиннее, чем L(T) фиксированы в объеме полимера, так как вовлечены в сетку макромолекул, образующую гель во всем объеме полимера. Сетку образуют макромолекулы, связанные между собой узлами - как химическими (в сетчатых полимерах), так и физическими (возникающими вследствие "переплетания" макромолекул).
Предлагаемый способ отличается от известного тем, что в нем точнее определена зависимость податливости полимерного материала от объемной доли макромолекул, вовлеченных в сетку (т.е. не расплавленных).
Достигается это тем, что на основе современных представлений о релаксации полимерных молекул под действием механического напряжения корректная форма указанной зависимости устанавливается следующим образом.
Упомянутая выше длина L(T) является критической величиной, разделяющей короткие "расплавленные" макромолекулы от больших формирующих гель макромолекул полимера. Механический модуль упругости (Юнга) определяется концентрацией узлов сетки (зацеплений) n:
E ≈ n
Объемная доля достаточно больших макромолекул равна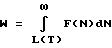
Количество физических зацеплений пропорционально количеству контактов между длинными макромолекулами, т.е. квадрату их объемной доли:
E ≈ n ≈ W2 (*),
что отличается от используемой в известном способе зависимости.
Таким образом, квадратный корень модуля Юнга линейных полимеров пропорционален объемной доле макромолекул с длиной цепи больше L(T).
В сетчатых полимерах помимо физических узлов (образованных зацеплениями длинных участков полимерных цепей) имеются химические узлы сетки, количество которых не меняется при сканировании по температуре. Поэтому для сетчатых полимеров выражение (*) принимает вид
E ~ W2+α•n,
где n - количество химических узлов, α - неизвестный коэффициент пропорциональности.
Слагаемое n обусловливает конечное значение модуля Юнга при исчезающе малых значениях W, т.е. на плато высокоэластичности. Поэтому, чтобы соотношение (*) было верным и для сетчатых полимеров, в качестве E следует подставлять модуль Юнга при данной температуре за вычетом модуля Юнга на плато высокоэластичности.
Зависимость L(T) хорошо изучена и для заданной скорости сканирования по температуре образца представляет собой известную логарифмическую зависимость
lg{L} ≈ (T-T0)
где T - температура стеклования полимера.
Поэтому производная квадратного корня модуля Юнга (уменьшенного на значение этого модуля на плато высокоэластичности, если таковое имеется т.е. если полимер сетчатый) по температуре пропорциональна весовой функции распределения полимера по логарифму длины макромолекул.
Согласно предлагаемому способу, весовую функцию молекулярно-массового распределения полимера определяют следующим образом: при сканировании по температуре с постоянной скоростью измеряют температурную зависимость модуля Юнга образца полимерного материала выше температуры стеклования полимера; производная квадратного корня модуля Юнга (уменьшенного на экстраполированное до данной температуры значение этого модуля на плато высокоэластичности, если полимер сетчатый) по температуре с точностью до постоянного множителя дает весовую функцию распределения полимера по логарифму длины макромолекул.
Пример. Определение функции молекулярно-массового распределения сшитого образца полиизоцианата
1. На изначально плоскую поверхность образца полимера воздействуют с постоянной силой полусферическим пуансоном, измеряя при этом расстояние, на которое пуансон продавливает поверхность полимера. При этом равномерно, т. е. с постоянной скоростью, повышают температуру образца. На чертеже показана полученная зависимость смещения пуансона от температуры. Это - термомеханическая кривая (ТМК). Смещение пуансона l при выбранной температуре T определяется длиной отрезка BE на чертеже. Модуль Юнга E, как известно, однозначно определяется смещением пунсона l давлением p на пунсон и радиусом пуансона R.
В наших целях достаточно воспользоваться величиной пропорциональной модулю Юнга, т. е. модуль отрезка 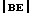 . Для сетчатого полимера модуль отрезка
. Для сетчатого полимера модуль отрезка 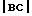 задает величину, соответствующую модулю Юнга на плато высокоэластичности и экстраполированную до температуры T. Длина отрезка
задает величину, соответствующую модулю Юнга на плато высокоэластичности и экстраполированную до температуры T. Длина отрезка 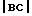 соответствует слагаемому l в выражении для модуля Юнга на стр. 3 описания. Поэтому W (весовая доля макромолекул, вовлеченных в сетку при данной температуре) пропорциональна корню
соответствует слагаемому l в выражении для модуля Юнга на стр. 3 описания. Поэтому W (весовая доля макромолекул, вовлеченных в сетку при данной температуре) пропорциональна корню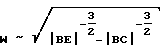
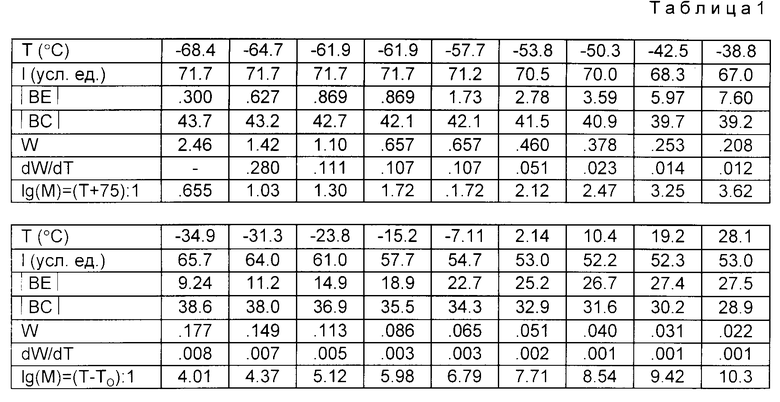
Удобно воспользоваться таблицей. Первые две строчки в ней - результаты измерений; остальные строки определяются первыми двумя. В седьмой строке таблицы представлены значения логарифма молекулярной массы M цепей, "плавящихся" при данной температуре. Единица измерения массы цепи - масса одного звена (таким образом M есть количество звеньев цепи).
В таблице показано определение функции молекулярно-массового распределения сшитого образца полиизоцианата по логарифму молекулярной массы.
Первые две строки отражают экспериментально зарегистрированную термомеханическую кривую образца сшитого полиизоцианата при нагреве образца со скоростью 1,25oC в 1 мин и нагрузке 50 г на полусферический пуансон радиусом 3 мм. Последняя строка представляет известную зависимость температуры плавления полимера от его молекулярной массы: при этом -75oC - температура начала сегментального движения молекул полимера.
Последние две строки определяют искомую функцию распределения.
Сущность изобретения: способ заключается в одновременном воздействии на образец пуансоном и температурой, повышаемой с постоянной скоростью в диапазоне от температуры стеклования полимера до температуры t полного его перехода в высоко-эластическое состояние, определение смещения пуансона для всего ряда значений температур и значений модуля Юнга E, соответствующих значениям температур. Кроме того, строят кривую E = f(t), на ней определяют участок, соответствующий плато высокоэластичности, значения модуля Юнга E0 этого участка экстраполируют прямой линией, а его значения на других участках уменьшают на E0 и определяют производную температурной зависимости от квадратного корня всех полученных при экстраполяции значений, которую выбирают в качестве параметра, по которому судят о молекулярно-массовом распределении полимера. 1 табл., 1 ил.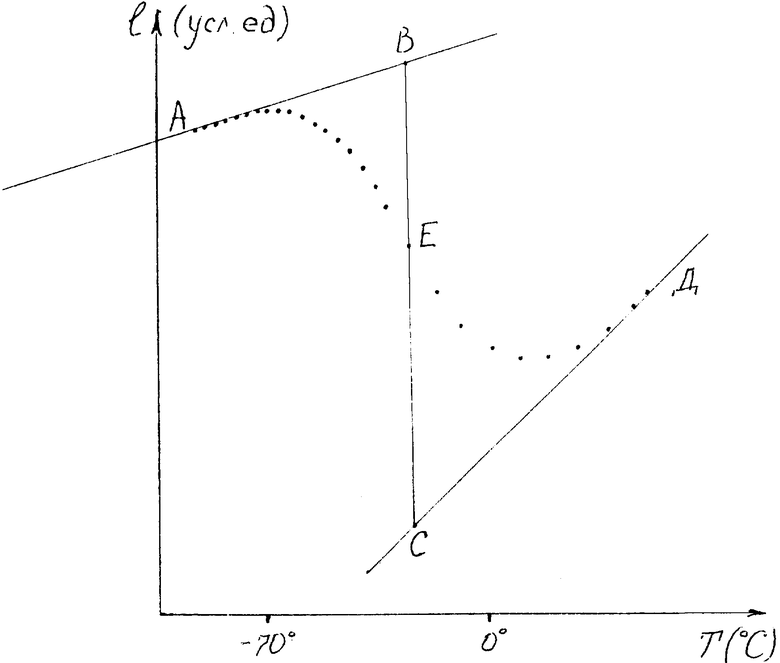
Способ определения молекулярно-массового распределения молекул полимера, заключающийся в одновременном воздействии на образец пуансоном и температурой t, которую повышают с постоянной скоростью в диапазоне от температуры стеклования полимера до температуры полного его перехода в высоко-эластическое состояние и определяют смещение пуансона для всего ряда значений температур указанного диапазона и параметр, по которому судят о молекулярно-массовом распределении полимера, отличающийся тем, что определяют модуль Юнга для указанных смещений пуансона и строят кривую Е f(t), определяют на ней участок, соответствующий плато высокоэластичности, значения модуля Юнга Е0 этого участка экстраполируют прямой линией, а его значения на других участках уменьшают на Е0 и определяют производную температурной зависимости от квадратного корня всех полученных при экстраполяции значений, которую выбирают в качестве параметра, по которому судят о молекулярно-массовом распределении полимера.
| Ольхов Ю.А., Иржак В.И., Батурин С.М | |||
| Новый метод определения молекулярно-массового распределения полимеров, блок-сополимеров и несшитых композиционных материалов на их основе | |||
| - Canada, Montreal, XXXIII-rd international jymposium, IUPAC on maoromolecules, 1990, Book Abstracts, section 2.1.7. |
Авторы
Даты
1998-02-20—Публикация
1993-06-28—Подача