Изобретение относится к области кодирования и передачи информации и может быть использовано в информационных электронных устройствах, звукозаписи, радиовещании, телевидении.
По своей технической сущности наиболее близким к заявляемому объекту является известный способ (прототип) аналого-цифрового и цифроаналогового преобразований [1], по которому аналоговый сигнал разбивается с помощью запускающих импульсов на периодические временные (тактовые) интервалы и в каждом интервале аналоговый сигнал преобразуется в кодированные импульсы в виде цифрового кода. Последний представляет собой последовательность определенным образом расставленных по времени счетных импульсов. По другому известному способу [2, стр. 232] , [3, стр. 125] эта последовательность представляет собой эквидистантно расположенные импульсы, число которых пропорционально значению кодируемого аналогового сигнала. Большим достоинством прототипа является его помехоустойчивость при передаче цифровой информации от передатчика по линиям связи или через эфир к приемнику. Недостатком прототипа является неизбежная ошибка цифрования аналогового сигнала, обусловленная квантовым характером этой операции, причем имеет место неопределенность как по амплитуде, так и по времени. Кроме того, поскольку генератор счетных импульсов должен работать на частоте, значительно превышающей тактовую, возникают проблемы преобразования высокочастотных аналоговых сигналов. К тому же цифрующие и децифрующие устройства достаточно сложны, что особенно проявляется в информационной системе, включающей в себя много приемников (цифровые звукозапись, радиовещание, телевидение и т.п.).
Другим известным техническим решением является способ частотно-модулированного преобразования [2, стр. 242] время-импульсного типа, в котором варьируют частоту импульсов, причем изменение частоты пропорционально изменению аналогового сигнала. В этом способе частота непрерывным образом связана с амплитудой аналогового сигнала. Однако при обратном преобразовании частотно-модулированного сигнала его делят на периодические временные интервалы и в пределах каждого интервала определяют частоту путем счета импульсов. При этом, во-первых, получают среднюю по интервалу частоту, во-вторых, количество импульсов является целочисленной величиной. Таким образом, и этому типу преобразования свойственна неопределенность (неточность) получения дискретного значения преобразованного аналогового сигнала.
Во всех способах преобразования аналогового сигнала импульсного типа получают сначала дискретные значения преобразованного сигнала, привязанные к их временным координатам, причем и временная координата и соответствующее ему значение определяются кодированными импульсами. Например, в [3, стр. 232, рис. 4.20] это значение представляет собой высоту заднего ступенчатого фронта импульса, полученного при обратном преобразовании. Затем применяют методы интерполяции, с помощью которых преобразуют дискретные значения в непрерывный сигнал (в [2, стр. 141] дискретные значения, подвергаемые интерполяции, названы узловыми точками).
В первом варианте заявляемого способа преобразования аналогового сигнала в дискретные значения преобразованного сигнала при прямом преобразовании выбирают значения постоянного множителя больше нуля и постоянной смещения такими, чтобы сумма произведения постоянного множителя на минимум аналогового сигнала и постоянной смещения была больше нуля. Умножают входной аналоговый сигнал на постоянный множитель, суммируют произведение с постоянной смещения и получают тем самым компилированный сигнал. В соответствии с синхронизирующими импульсами генерируют кодирующий сигнал в виде кодирующих импульсов непрямоугольной формы, минимум которых меньше или равен рабочему минимуму больше нуля, а максимум больше или равен рабочему максимуму при отношении рабочего максимума к рабочему минимуму, большем отношения максимума к минимуму для компилированного сигнала. Выбирают значения постоянного коэффициента больше нуля и постоянной сдвига такими, чтобы сумма умноженного на постоянный коэффициент произведения максимума компилированного сигнала на рабочий минимум и постоянной сдвига была меньше эталонной постоянной, а сумма умноженного на постоянный коэффициент произведения минимума компилированного сигнала на рабочий максимум и постоянной сдвига была больше эталонной постоянной. Умножают кодирующий сигнал на компилированный сигнал, произведение умножают на постоянный коэффициент, суммируют с постоянной сдвига и получают модулированный сигнал. Сравнивают модулированный сигнал с эталонной постоянной. Получают кодированные импульсы, ступенчатые корневые фронты которых совпадают с моментами равенства модулированного сигнала и эталонной постоянной. При обратном преобразовании генерируют декодирующий сигнал, равный отношению кодирующего сигнала к постоянному коэффициенту пропорциональности больше нуля и синхронизованный с временной шкалой кодированных импульсов путем использования синхронизирующих импульсов. Определяют значения декодирующего сигнала в моменты ступенчатых корневых фронтов кодированных импульсов. На полученные значения декодирующего сигнала делят отношение разности эталонной постоянной и постоянной сдвига к постоянному коэффициенту, из частного вычитают произведение коэффициента пропорциональности на постоянную смещения и получают тем самым дискретные значения преобразованного аналогового сигнала, временное положение которых соответствует ступенчатым корневым фронтам кодированных импульсов.
Во втором варианте заявляемого способа умножают входной аналоговый сигнал на постоянный множитель больше нуля, суммируют произведение с постоянной смещения и получают тем самым компилированный сигнал. В соответствии с синхронизирующими импульсами генерируют кодирующий сигнал в виде кодирующих импульсов непрямоугольной формы, минимум которых меньше разности эталонной постоянной и максимума компилированного сигнала, а максимум больше разности эталонной постоянной и минимума компилированного сигнала. Производят суммирование компилированного сигнала с кодирующим сигналом и получают суммарный сигнал. Сравнивают суммарный сигнал с эталонной постоянной. Получают кодированные импульсы, ступенчатые корневые фронты которых совпадают с моментами равенства суммарного сигнала и эталонной постоянной. При обратном преобразовании генерируют в соответствии с синхронизирующими импульсами декодирующий сигнал, равный произведению коэффициента пропорциональности больше нуля на кодирующий сигнал. Определяют значения декодирующего сигнала в моменты ступенчатых корневых фронтов кодированных импульсов. Полученные значения декодирующего сигнала вычитают из произведения коэффициента пропорциональности на разность эталонной постоянной и постоянной смещения и получают тем самым дискретные значения преобразованного аналогового сигнала.
В третьем варианте заявляемого способа умножают входной аналоговый сигнал на постоянный множитель, суммируют произведение с постоянной смещения и получают тем самым компилированный сигнал. Генерируют кодирующий сигнал в виде периодической последовательности кодирующих импульсов непрямоугольной формы, минимум которых меньше минимума компилированного сигнала, а максимум больше максимума компилированного сигнала. Сравнивают компилированный сигнал с кодирующим сигналом. Получают кодированные импульсы, ступенчатые корневые фронты которых совпадают с моментами равенства компилированного и кодирующего сигналов. При обратном преобразовании генерируют в соответствии с синхронизирующими импульсами декодирующий сигнал, равный произведению коэффициента пропорциональности больше нуля на кодирующий сигнал. Определяют значения декодирующего сигнала в моменты ступенчатых корневых фронтов кодированных импульсов. Из полученных значений декодирующего сигнала вычитают произведение коэффициента пропорциональности на постоянную смещения и получают дискретные значения преобразованного аналогового сигнала.
Математическое обоснование заявляемого способа заключается в следующем. Пусть A(t) - входной аналоговый сигнал, C(t) - кодирующий сигнал, E - эталонная постоянная, K - больший нуля постоянный множитель, S - постоянная смещения, B - больший нуля постоянный коэффициент, D - постоянная сдвига. Умножаем A(t) на K, суммируем произведение с S и получаем компилированный сигнал K A(t) + S. В первом варианте заявляемого способа умножаем компилированный сигнал на C(t), произведение умножаем на B, суммируем с D и получаем модулированный сигнал [K A(t) + S ] C(t) B + D. Направляем его в решающее устройство, с помощью которого решаем уравнение
[K A(t) + S] C(t) B + D = E. (1)
Находим множество значений tr , где r = 1,2,3, ..., являющихся корнями уравнения (1). Для каждого значения tr имеем равенство:
[K A(tr) + S ] C(tr) B + D = E, (2)
из которого следует:
A(tr) = K-1[E - D) B-1 C-1(tr) - S ] ≈ (E - D) B-1P C-1(tr) - P S, (3)
где
P - больший нуля коэффициент пропорциональности.
Во втором варианте заявляемого способа компилированный сигнал K A(t) + S суммируем с кодирующим сигналом C(t) и получаем суммарный сигнал. Направляем суммарный сигнал в решающее устройство, с помощью которого решаем уравнение
K A(t) + S + C(t) = E (4)
Находим множество значений tr, являющихся корнями уравнения (4). Для каждого значения tr имеем равенство:
K A(tr) + S + C(tr) = E, (5)
из которого следует:
A(tr) = K-1[E - S - C(tr)] ≈ P (E-S)-P C(tr). (6)
В третьем варианте заявляемого способа компилированный и кодирующий сигналы направляем в решающее устройство, с помощью которого решаем уравнение
K A(t) + S = C(t). (7)
Находим множество значений tr, являющихся корнями уравнения (7). Для каждого значения tr имеем равенство:
K A(tr) + S = C(tr), (8)
из которого следует:
A(tr)= K-1[C(tr) - S] ≈ P C(tr) - P S. (9)
Выражения (1) - (9) показывают, что, если в кодирующем устройстве генерировать кодирующий сигнал и используемые постоянные, составить уравнение, включающее аналоговый и кодирующий сигналы вместе с необходимыми постоянными, решить уравнение с помощью решающего устройства, найдя его корни, направить информацию о корнях в декодирующее устройство, в котором генерировать необходимые постоянные и декодирующий сигнал, пропорциональный кодирующему, зафиксировать значения декодирующего сигнала в моменты корней, получив их в фазе, равной фазе корневых значений кодирующего сигнала, и выполнить с полученными значениями декодирующего сигнала необходимые арифметические операции, то на выходе декодирующего устройства получим дискретные значения преобразованного аналогового сигнала, пропорциональные корневым значениям входного аналогового сигнала. В качестве решающего используем известные устройства: для первого и второго вариантов - компаратор, в котором сравнивают переменный сигнал с эталонной постоянной E, для третьего варианта - сравнивающее устройство, в котором сравнивают два переменных сигнала. Естественно, что уравнения составляются с учетом типа решающего устройства. Для получения в декодирующем устройстве значения декодирующего сигнала в фазе, равной фазе корневого значения кодирующего сигнала, генерируем в кодирующем устройстве синхронизирующие импульсы, передаваемые вместе с информацией о корнях в декодирующее устройство. Поскольку в заявляемом способе преобразуются мгновенные значения аналогового сигнала в моменты корней решаемых уравнений, информация о корнях, передаваемая из кодирующего устройства в декодирующее, должна представлять собой импульсы, называемые кодированными, имеющие ступенчатые фронты в моменты корней. Такие импульсы можно получить либо непосредственно в используемых решающих устройствах, либо на основе импульсов, полученных в решающих устройствах.
Умножение во всех вариантах на больший нуля коэффициент пропорциональности P применяют для того, чтобы генерировать в декодирующем устройстве декодирующий сигнал, пропорциональный кодирующему.
Уравнения (1), (4), (7) и равенства (2), (5), (8) математически описывают прямое преобразование дискретных значений аналогового сигнала в кодированную форму - множество tr - в кодирующем устройстве, соотношения (3), (6), (9) - обратное преобразование кодированной формы tr в дискретный аналоговый сигнал в декодирующем устройстве. Рассмотрим необходимые условия и требования, выполнение которых позволит осуществить такое преобразование.
Как видно из (1) - (9), кодирующий сигнал C(t) не должен состоять из прямоугольных импульсов. В противном случае множество tr будет содержать случайно расположенные корни. Очевидно, что для получения из дискретных значений после преобразования непрерывного аналогового сигнала, максимально близкого к исходному аналоговому сигналу, необходимо, чтобы C(t) был периодическим сигналом. Чем выше частота этого сигнала, тем точнее воспроизводится непрерывный аналоговый сигнал. В пределах периода кодирующий импульс может быть как одиночным, так и в виде пачки импульсов, однако понятно, что применение пачки импульсов просто равносильно увеличению частоты кодирующего сигнала. Форма импульсов может быть достаточно разнообразной: симметричной или несимметричной относительно максимума импульса, со ступенчатым передним фронтом и монотонно убывающим от максимума к минимуму задним фронтом, с монотонно возрастающим от минимума к максимуму передним фронтом и ступенчатым задним фронтом и т.д. Практически форму импульса выбирают исходя из наибольшей простоты, надежности, стабильности, точности электронных схем, генерирующих кодирующий сигнал в кодирующем устройстве и декодирующий сигнал в декодирующем устройстве.
В первом варианте из (1), (2), (3) следует, что рабочие области изменения компилированного и кодирующего сигналов не должны включать нулевую точку, т. к. , если какой-либо из сигналов стремится или равен нулю, другой сигнал стремится или равен бесконечности. Для устранения этого путем выбора постоянных K и S устанавливают минимум компилированного сигнала большим нуля и генерируют кодирующий сигнал с большим нуля рабочим минимумом. Здесь очевидно выполнение следующих соотношений:
(K A(t) + S)max = K Amax + S,
(K A(t) + S)min = K Amin + S,
где
Amax и Amin - соответственно максимальное и минимальное значения аналогового сигнала. Нижнее равенство используют для установления минимума компилированного сигнала больше нуля.
Определим максимум Cmax и минимум Cmin кодирующего импульса. Используя (1), найдем сначала минимальное значение максимума C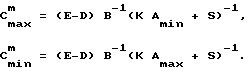
Для уверенного срабатывания компаратора при A(t), близких или равных Amax и Amin, вводим значения рабочего максимума C
C
C
из которых следует
E < (K Amin + S) C
E > (K Amax + S) C
Объединяя (12) и (13), получаем
(K Amax+ S)C
или
(K Amax+ S) (K Amin+ S)-1 < C
Неравенство (14) может выполняться не только для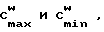 
удовлетворяющих (10) и (11) при определенных E, B и D, но и для других положительных значений 
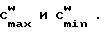При этом для выбранного компаратора с эталонной постоянной E неравенствам (12) и (13) удовлетворяют путем выбора постоянных B и D, возможность чего обеспечивается при выполнении неравенства (14). Для расширения области параметров кодирующих импульсов, которые можно использовать для преобразования, устанавливаем параметры кодирующих импульсов Cmax ≥ C
Во втором варианте определим параметры кодирующих импульсов Cmax и Cmin. Из (4) находим C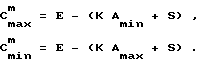
Для того, чтобы в компараторе были получены корни уравнения (4), соответствующие значениям аналогового сигнала в пределах от Amax до Amin, и при этом компаратор устойчиво срабатывал, устанавливаем параметры кодирующего сигнала:
Cmax > C
Cmin > C
Что касается постоянных K и S компилированного сигнала, то, как видно из (15) и (16), при больших абсолютных значениях в них правых частей становятся абсолютно большими Cmax и/или Cmin. Хотя с точки зрения получения конечного результата это совершенно не существенно, тем не менее путем выбора K и S можно оптимизировать параметры C(t).
В третьем варианте необходимо путем выбора постоянного множителя K и постоянной смещения S установить минимум и максимум компилированного сигнала в пределах рабочего диапазона сравнивающего устройства. Максимум кодирующих импульсов необходимо установить большим максимума компилированного сигнала, а минимум - меньшим минимума компилированного сигнала:
Cmax > C
Cmin < C
На фиг.1 приведена графическая информация, иллюстрирующая первый вариант заявляемого способа.
На фиг. 1.1 показан кодирующий импульс. В качестве примера приведена функция C(t) = cos2(πt/ T) + C
На фиг.1.2 приведен пример фрагмента аналогового сигнала вида A(t) = 0,5 sin(πt/ T) в пределах одного периода.
На фиг. 1.3 приведен модулированный сигнал [K A(t) + S] C(t) B + D, поступивший в компаратор, в котором его сравнивают с эталонной постоянной E. Конкретные константы таковы: K = 0,6, S = 0,4, B = 3, D = 0, E = 0,27. Для этих констант отношение максимума компилированного сигнала к его минимуму равно 7, т. е. выполняется неравенство (14), значения модулированного сигнала, соответствующие: произведению максимума компилированного сигнала на C
На фиг. 1.4 показан полученный после компаратора кодированный импульс прямоугольной формы, передний и задний ступенчатый фронты которого являются корневыми и их временные координаты tr и tr+1 являются моментами равенства модулированного сигнала и эталонной постоянной.
На фиг.1.5 показан прямоугольный импульс вместе с синхронизирующим импульсом.
На фиг.1.6 показаны кодированные импульсы в виде коротких импульсов, полученных, например, путем дифференцирования прямоугольного импульса, и синхронизирующий импульс.
На фиг.1.7 показан один период функции (E - D) B-1 P C-1(t) - P S при P = K-1, выработанной в декодирующем устройстве. Значения этой функции в моменты времени tr и tr+1 равны соответственно A(tr) и A(tr+1) фиг.1.2.
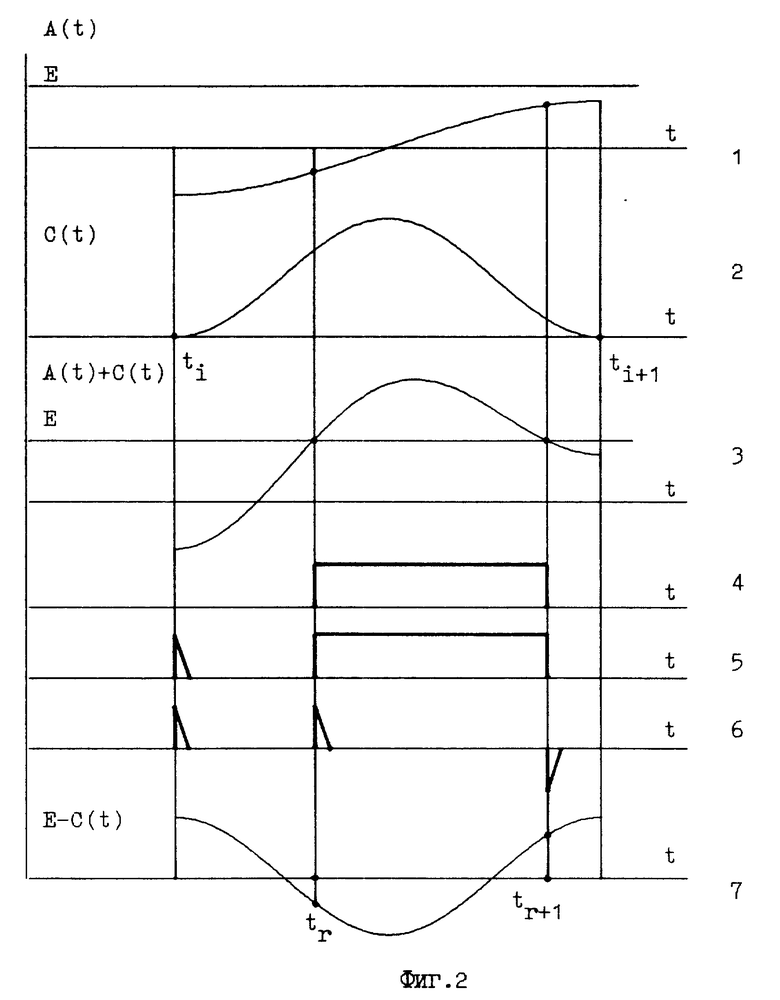
На фиг.2 приведена графическая информация, иллюстрирующая второй вариант заявляемого способа.
На фиг.2.1 показан пример фрагмента аналогового сигнала вида A(t) = sin(πt/ T) в пределах -T/2 < t < T/2, где T - период кодирующей функции, вместе с эталонной постоянной E. В компилированном сигнале K A(t) + S K=1, S=0.
На фиг.2.2 приведен пример кодирующего импульса C(t) = Cmax cos2(πt/ T) в пределах одного периода. Cmax > E - Amin, Cmin = 0 < E - Amax, т.е. выполняются неравенства (15) и (16). t(i) и t(i+1) - начальная и конечная точки периода.
На фиг. 2.3 приведен суммарный сигнал A(t) + C(t), поступивший в компаратор, в котором его сравнивают с эталонной постоянной E.
На фиг. 2.4 показан полученный после компаратора кодированный импульс прямоугольной формы, передний и задний ступенчатые фронты которого являются корневыми и их временные координаты tr и tr+1 являются моментами равенства суммарного сигнала и эталонной постоянной.
На фиг. 2.5 показан прямоугольный импульс вместе с синхронизирующим импульсом.
На фиг.2.6 показаны кодированные импульсы в виде коротких импульсов, полученных, например, путем дифференцирования прямоугольного импульса, и синхронизирующий импульс.
На фиг. 2.7 показана функция E-C(t), где E и C(t) выработаны в декодирующем устройстве. Значения этой функции и функции A(t) фиг.2.1 в моменты времени tr и tr+1 равны.
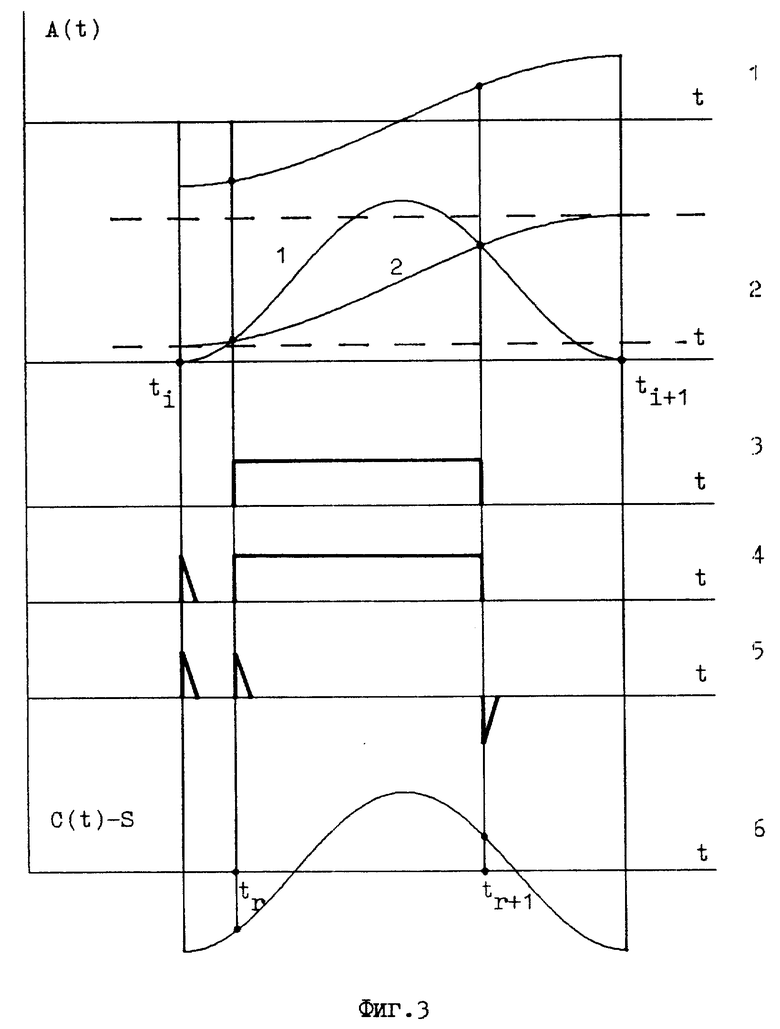
На фиг.3 приведена графическая информация, иллюстрирующая третий вариант заявляемого способа.
На фиг.3.1 показан пример фрагмента аналогового сигнала вида A(t) = sin(πt/ T) в пределах -T/2 < t < T/2, где T - период кодирующего сигнала.
На фиг.3.2 показаны сигналы, направленные в сравнивающее устройство: 1- пример кодирующего импульса вида C(t) = 2,5 cos2(πt/ T) в пределах одного периода, ti и ti+1 - начальная и конечная точки периода; 2 - компилированный сигнал K A(t) + S , для которого K=1, S=1,25. Пунктирные линии - границы рабочего диапазона сравнивающего устройства. Выполнение неравенств (17) и (18) очевидно.
На фиг. 3.3 показан полученный после сравнивающего устройства кодированный импульс прямоугольной формы, передний и задний ступенчатые фронты которого являются корневыми и их временные координаты tr и tr+1 являются моментами равенства компилированного и кодирующего сигналов.
На фиг.3.4 показан прямоугольный импульс вместе с синхронизирующим импульсом.
На фиг.3.5 показаны кодированные импульсы в виде коротких импульсов, полученных, например, путем дифференцирования прямоугольного импульса, и синхронизирующий импульс .
На фиг. 3.6 показана функция C(t) - S, выработанная в декодирующем устройстве при P=1. Значения этой функции и функции A(t) фиг.3.1 в моменты времени tr и tr+1 равны.
При использовании кодирующего импульса со ступенчатым передним или задним фронтом после компаратора или сравнивающего устройства вырабатывают кодированные импульсы, например, прямоугольной формы, в которых один из ступенчатых фронтов совпадает со ступенчатым фронтом кодирующего импульса. Очевидно, что ступенчатый фронт кодированного импульса, совпадающий со ступенчатым фронтом кодирующего импульса, не может быть использован для получения дискретного значения преобразованного аналогового сигнала, так как он не является корневым. И если такой прямоугольный импульс дифференцируется, то один из двух полученных импульсов не имеет ступенчатого фронта, являющегося корневым. Импульс, не имеющий ни одного ступенчатого корневого фронта, по определению не является кодированным и нет необходимости передавать его в декодирующее устройство.
Вырабатываемые в кодирующем устройстве вместе с кодирующим сигналом синхронизирующие импульсы используют для синхронизации временных шкал кодированных импульсов и генератора декодирующего сигнала. Для того чтобы синхронизирующие импульсы не совпадали со ступенчатыми корневыми фронтами кодированных импульсов, их вставляют в точках минимума или максимума кодирующего импульса. При выполнении неравенств (12), (13), (15), (16), (17), (18) вблизи минимума и максимума кодирующего импульса существуют так называемые "запретные зоны" для ступенчатых корневых фронтов кодированных импульсов, в которые они не попадают. Длительности "запретных зон" равны: в окрестности минимума кодирующего импульса - времени, в течение которого кодирующий сигнал изменяется, уменьшаясь от C
Приведенная графическая информация показывает, что при использовании кодирующего периодического импульса в виде моноимпульса с монотонно возрастающим передним и монотонно убывающим задним фронтами за один период получают два дискретных значения аналогового сигнала. При использовании кодирующего импульса, в котором один из фронтов является ступенчатым, за один период получают одно дискретное значение аналогового сигнала. Если использовать кодирующий импульс в виде пачки моноимпульсов, то число дискретных значений соответственно возрастает.
Восстановление дискретных значений аналогового сигнала в декодирующем устройстве осуществляют в различных режимах. В одном из них генератор декодирующего сигнала работает непрерывно. В момент прихода ступенчатого корневого фронта кодированного импульса определяют значение декодирующего сигнала, производят с ним арифметические операции в соответствии с применяемым вариантом и результат направляют в последующие устройства. Если для фиксации и передачи дискретного значения аналогового сигнала требуется время, используют режим остановки. Для этого запущенный генератор декодирующего сигнала останавливают ступенчатым корневым фронтом кодированного импульса, фиксируют остановленное значение декодирующего сигнала, обрабатывают, передают результат в последующие устройства и подготавливают генератор декодирующего сигнала к восстановлению следующего дискретного значения аналогового сигнала. В тех случаях, когда восстановленное дискретное значение близко по времени к точкам минимума или максимума кодирующего импульса, для перечисленных выше операций используют "запретные зоны". Обозначим минимально необходимую длительность "запретной зоны" Δtz. Очевидно, что с точки зрения наиболее рационального использования фактора времени желательно выполнение неравенства Δtz << T. Если при использовании какой-либо формы кодирующего импульса неравенств (12), (13), (15), (16), (17), (18) недостаточно для получения длительности "запретной зоны", равной Δtz, используют кодирующий импульс с плоским максимумом и/или минимумом, причем длительность плоской части равна Δtz. Кроме того возможны режимы восстановления с использованием задержки поступивших в кодирующее устройство импульсов.
Сравнивая между собой два способа передачи кодированной информации - прямоугольными или короткими импульсами, полученными, например, из прямоугольного путем его дифференцирования, - заметим, что с точки зрения минимального потребления энергии кодирующим устройством (в первую очередь его выходными каскадами), преимущество имеют короткие импульсы, поскольку площадь, занимаемая ими, значительно меньше площади прямоугольного импульса.
Приведенная графическая информация, а также вышеизложенное показывают, что с помощью заявляемого способа можно преобразовывать аналоговые сигналы любой полярности в том числе и знакопеременные. При этом в качестве решающих устройств можно использовать компараторы и сравнивающие устройства с любыми рабочими параметрами.
Таким образом, в отличие от прототипа, в котором информации об амплитуде аналогового сигнала заключена в цифровом коде, в заявляемом способе эта информация заключена во временной координате ступенчатого корневого фронта кодированного импульса, являющейся для определенного значения аналогового сигнала функцией формы кодирующих импульсов, а для выбранной формы кодирующего импульса - непрерывной функцией аналогового сигнала. Ввиду этого заявляемый способ можно назвать функционально-временным преобразованием.
Приведем сравнительные характеристики прототипа и заявляемого способа.
1. Информативность.
В прототипе за один тактовый период получают одно дискретное значение аналогового сигнала.
В заявляемом способе при использовании кодирующего импульса в виде монотонно изменяющихся переднего и заднего фронтов получают за один период два дискретных значения аналогового сигнала.
2. Точность преобразования.
В прототипе преобразованное значение является неопределенным в пределах одного уровня квантования как по амплитуде, так и по времени.
В заявляемом способе получают точное дискретное значение с точной привязкой по времени.
3. Число передаваемых в декодирующее устройство импульсов на одно дискретное значение аналогового сигнала, не считая синхронизирующих импульсов.
В прототипе число счетных импульсов в пределах одного тактового периода велико и оно растет по мере увеличения точности квантования.
В заявляемом способе одно дискретное значение передается одним коротким импульсом.
4. Сложность электронных устройств.
В прототипе используются сложные цифровые схемы как в кодирующем, так и в декодирующем устройствах.
В заявляемом способе могут быть использованы довольно простые устройства для умножения и сложения сигналов, деления конкретных значений, умножения их на постоянную и генерирования периодических импульсов непрямоугольной формы.
5. Помехоустойчивость при передаче кодированной информации по линиям связи или через эфир.
Помехоустойчивость прототипа против амплитудных искажений известна. Помехоустойчивость заявляемого способа обеспечивается тем, что амплитудные искажения не сдвигают по времени ступенчатый корневой фронт кодированного импульса.
Проведенное сравнение свидетельствует о существенных преимуществах заявляемого способа.
Возможность реализации заявляемого способа не вызывает сомнений, поскольку операции умножения, деления, сложения и вычитания сигналов, умножения их на большую нуля постоянную (т.е. их усиление или ослабление), а также генерация периодических импульсов непрямоугольной формы в электронике давно известны и широко применяются. Точность преобразования зависит от точности генерирования в декодирующем устройстве функций, связанных с соответствующими функциями, генерированными в кодирующем устройстве, через больший нуля постоянный коэффициент пропорциональности, а также от точности выполнения арифметических операций.
Литература
1. Сворень Р. Электроника общения. Журнал "Наука и жизнь", N 10, с. 2-11, вкладки II-III, 1986.
2. Преобразование информации в аналого-цифровых вычислительных устройствах. Под ред. Г.М.Петрова. Москва, "Машиностроение", 1973.
3. Б. В. Анисимов, В.Н.Четвериков. Преобразование информации для ЭЦВМ. Москва, "Высшая школа", 1968.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПРЕОБРАЗОВАНИЯ АНАЛОГОВОГО СИГНАЛА | 1996 |
|
RU2118045C1 |
| СПОСОБ ПРЕОБРАЗОВАНИЯ АНАЛОГОВОГО СИГНАЛА | 1995 |
|
RU2099866C1 |
| МНОГОРОТОРНЫЙ ДВИГАТЕЛЬ ВНУТРЕННЕГО СГОРАНИЯ | 2005 |
|
RU2305785C2 |
| МНОГОРОТОРНЫЙ ДВИГАТЕЛЬ ВНУТРЕННЕГО СГОРАНИЯ | 2006 |
|
RU2351781C2 |
| Устройство для определения экстремумов электрического сигнала | 1988 |
|
SU1645940A1 |
| Устройство для определения экстремумов | 1981 |
|
SU985749A1 |
| Имитатор случайных процессов | 1976 |
|
SU796881A1 |
| Способ временной синхронизации системы связи на основе ортогонального частотного разделения каналов с мультиплексированием по преамбуле | 2015 |
|
RU2609774C2 |
| СПОСОБ ДИСКРЕТНОГО ЗАДАНИЯ ФАЗОВОГО СДВИГА МЕЖДУ ДВУМЯ МОНОХРОМАТИЧЕСКИМИ ГАРМОНИЧЕСКИМИ ИЗНАЧАЛЬНО СИНХРОННЫМИ СИГНАЛАМИ, И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2013 |
|
RU2534929C2 |
| Устройство для автоматического определения скоростей распространения сейсмических волн | 1975 |
|
SU600495A1 |
Изобретение относится к области кодирования и передачи информации и может быть использовано в информационных электронных устройствах, звукозаписи, радиовещании, телевидении. Изобретение состоит в том, что при прямом преобразовании в соответствии с синхронизирующими импульсами генерируют кодирующий сигнал в виде периодических импульсов непрямоугольной формы. Умножают аналоговый сигнал на постоянный множитель больше нуля и складывают с постоянной смещения, получая компилированный сигнал. В первом варианте компилированный сигнал умножают на кодирующий сигнал и на постоянный коэффициент больше нуля, суммируют с постоянной сдвига и результат сравнивают с эталонной постоянной. Во втором варианте складывают компилированный и кодирующий сигналы и результат сравнивают с эталонной постоянной. В третьем варианте сравнивают компилированный и кодирующий сигналы. Формируют импульсы, ступенчатые корневые фронты которых совпадают с моментами равенства сравниваемых величин. При обратном преобразовании в соответствии с синхронизирующими импульсами формируют декодирующий сигнал, равный для первого варианта отношению кодирующего сигнала к постоянному коэффициенту пропорциональности больше нуля, для второго и третьего вариантов - их произведению. Фиксируют значения декодирующего сигнала в моменты ступенчатых корневых фронтов. В первом варианте на полученные значения декодирующего сигнала делят отношение разности эталонной постоянной и постоянной сдвига к постоянному коэффициенту и из частного вычитают произведение коэффициента пропорциональности на постоянную смещения. Во втором варианте значения декодирующего сигнала вычитают из произведения коэффициента пропорциональности на разность эталонной постоянной и постоянной смещения. В третьем варианте из значений декодирующего сигнала вычитают произведение коэффициента пропорциональности на постоянную смещения. В итоге получают дискретные значения преобразованного аналогового сигнала. Технический результат - устранение ошибок преобразования, связанных с неопределенностью в пределах интервала дискретизации. 3 с.п.ф-лы, 3 ил.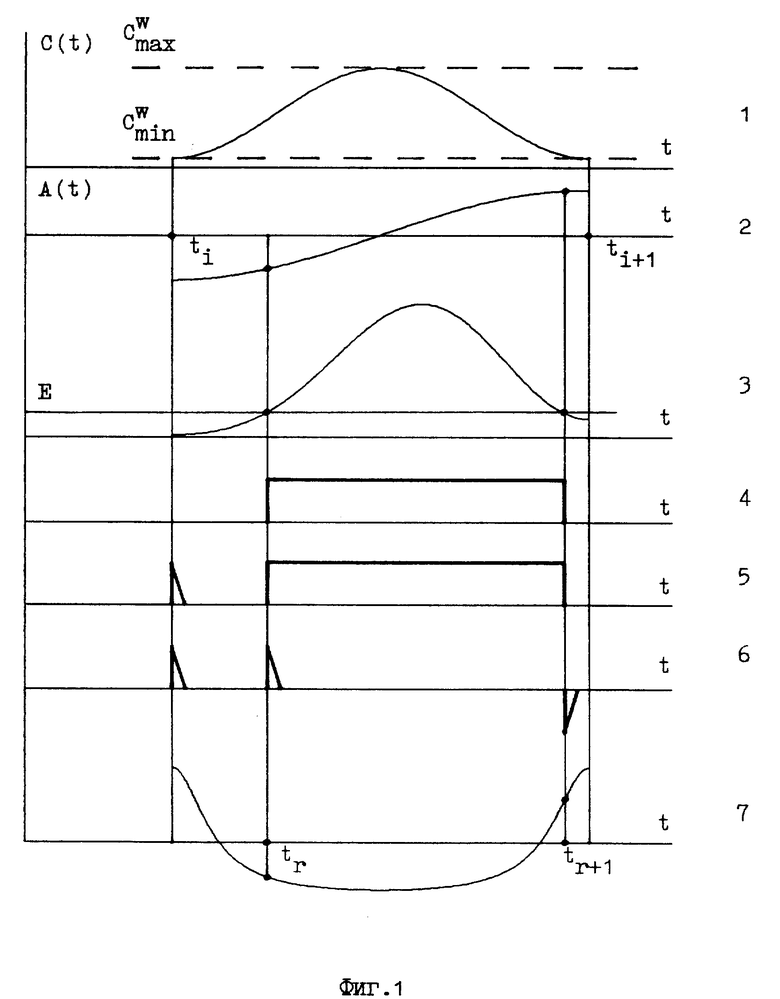
| СПОСОБ ПЕРЕДАЧИ ДИСКРЕТНЫХ СИГНАЛОВ ПО РАДИОКАНАЛАМ | 1972 |
|
SU430506A1 |
| Устройство для кодирования аналоговых сигналов | 1985 |
|
SU1316091A1 |
| Рекуперативный воздухонагреватель с использованием в качестве топлива жидких горючих отходов | 2002 |
|
RU2224185C1 |
| US 5010347, 23.04.91 | |||
| DE 3400665 A1,18.07.85 | |||
| Способ размножения копий рисунков, текста и т.п. | 1921 |
|
SU89A1 |
| Домовый номерной фонарь, служащий одновременно для указания названия улицы и номера дома и для освещения прилежащего участка улицы | 1917 |
|
SU93A1 |
| Сворень Р | |||
| Электроника общения | |||
| Наука и жизнь, N 10, 1986, с.2 - 11, вкладки II - III | |||
| Преобразование информации в аналого-цифровых вычислительных устройствах / Под ред.Петрова Г.М | |||
| Приспособление для склейки фанер в стыках | 1924 |
|
SU1973A1 |
