Изобретение относится к компьютерному проектированию и компьютерному дизайну, и в частности к системе и способу улучшенного параметрического геометрического моделирования.
Предшествующий уровень техники
В системах геометрического моделирования типа систем, входящих в продукцию компьютерного проектирования (АП), пользователь может, например, описывать двумерные геометрические формы, используя профиль в качестве признака для описания поперечного сечения предмета. Профиль представляет собой либо замкнутую непрерывную двухмерную область, используемую для образования геометрического тела, либо, если профиль используется для образования поверхности, профиль может быть непрерывным набором двухмерных кривых. Профиль используют для образования более сложных пространственных геометрических форм путем развертки или экструдирования поперечного сечения, которое оно очерчивает. Кроме того, пользователь объемного моделирования может развертывать два разных профиля, которые лежат в двух разных плоскостях, и пересекать, объединять и вычерчивать один развертываемый профиль из другой развертки для образования более полной трехмерной формы.
Часто бывает так, что геометрический профиль, используемый для представления объекта типа механической детали, необходимо моделировать в виде чертежа изменений объекта. Желательно, чтобы такая модификация производилась посредством воздействия на величины, используемые для описания характеристик профиля, а не обеспечения непосредственного повторного задания геометрических форм профиля. Таким образом, пользователь может редактировать коэффициенты уравнений в системе уравнений эскиза путем непосредственного редактирования размеров посредством системы восстановления связанных размеров и уравнений связи. Способность осуществлять этот тип модификации называется параметрическим геометрическим моделированием.
Компьютеризованные системы, которые дают возможность пользователю осуществлять параметрические геометрическое моделирование, обычно используют устройство для решения уравнений, предназначенное для решения семейств алгебраических уравнений, описывающих геометрические профили. Такие устройства для решения уравнений описаны в литературе и используют один из двух методов: метод использования числового алгоритма Ньютона-Рафсона или конструктивный алгоритм, имитирующий построение с помощью линейки и циркуля. Пример последнего имеется в работе Дж. К.Х. Чанга и М.Д.Скассела "Сравнение вариационного и параметрического проектирования", Системы машиностроения, Издательство Ауэрбах.
Часто бывает необходимо модифицировать величины профиля, используемые для описания характеристик эскиза, когда система уравнений, используемых для описания профиля, неполная или переполнена. Однако оба упомянутых выше способа решения уравнений имеют присущие им недостатки, когда их применяют для решения систем алгебраических уравнений, которые неполные или переполнены. Система уравнений считается неполной, когда система уравнений является недостаточной для определения соответствующей геометрической формы, описываемой такой системой уравнений. Подобно этому, система уравнений считается переполненной, если в этой системе уравнений больше, чем необходимо для определения соответствующей геометрической формы, описываемой уравнениями.
Способом конструктивного алгоритма нельзя определить некомплексное решение (корень) для системы неполных алгебраических уравнений. Более того, такой подход не может располагать уравнения в соответствии с приоритетом и выбирать подходящее и желательное решение для системы, имеющей больше необходимого количества уравнений. С другой стороны, способ численного алгоритма страдает не только такими же присущими недостатками, приведенными в отношении конструктивного способа, но, кроме того, не способен использовать эвристику для выбора наиболее подходящего решения проектирования объекта по конечному множеству решений.
Краткое изложение существа изобретения
Целью настоящего изобретения является создание системы и способа для решения систем уравнений, которые характеризуют параметрические геометрические профили и дают возможность видоизменять объект при изменениях конструкции объекта путем модификации величин, используемых для описания характеристик профиля, а не непосредственного нового задания геометрических форм профиля.
Другой целью настоящего изобретения является создание системы и способа для определения некомплексного решения неполной системы алгебраических уравнений и для изменения значений, используемых для описания характеристик профиля, когда система неполная.
Еще одной целью настоящего изобретения является создание системы и способа, которые применяют эвристику к этим уравнениям для определения желательных решений переполненной системы уравнений.
Еще одной целью настоящего изобретения является создание системы и способа для решения описывающих геометрическую формул уравнений, которые располагают уравнения в соответствии с приоритетом для установления определяемых пользователем предпочтительных уравнений над уравнениями, выводимыми системой.
Для достижения этих и других целей предлагается система и способ, которые уникально решают систему алгебраических уравнений, описывающих двухмерные геометрические профили или проекции трехмерных профилей объектов на двухмерную плоскость. Поскольку формой профиля управляет решение, получаемое из системы алгебраических уравнений, настоящее изобретение изменяет значения, используемые для представления характеристик профиля, и тем самым модифицирует форму профиля.
Систему и способ образования параметрического профиля объекта, подлежащего моделированию, в соответствии с настоящим изобретением принимают входной сигнал от пользователя в форме уравнений, вырабатывают следующие уравнения, свойственные описанию профиля, располагают уравнения в соответствии с приоритетом по определенным классам, сортируют расположенные в соответствии с приоритетом уравнения, создавая тем самым упорядоченный перечень решаемых уравнений, решают классифицированные уравнения в том порядке, в котором они появляются в перечне решаемых уравнений, и вырабатывают профиль геометрических объектов, создаваемых по решениям решенных уравнений. Система и способ автоматически связывают неизвестные переменные в любых неполных системах уравнений, основываясь на эвристике, и использует любые уравнения, содержащие посторонние корни, для определения и разрешения конфликтных ситуаций среди подлежащих использованию уравнений, предназначенных для формирования профиля.
Краткое описание чертежей
Эти и другие особенности и преимущества настоящего изобретения станут понятны специалистам в данной области техники из последующего подробного описания предпочтительных вариантов осуществления со ссылкой на прилагаемые чертежи, из которых:
фиг. 1 иллюстрирует схематическое представление примерной системы обработки согласно настоящему изобретению;
фиг. 2 изображает блок-схему предпочтительного варианта осуществления настоящего изобретения;
фиг. 3 изображает более подробную блок-схему части уравнений классификации, соответствующей варианту, показанному на фиг. 2 блок-схемы, согласно настоящему изобретению;
фиг. 4a представляет схему примерного переполненного класса уравнений;
фиг. 4b представляет схему примерного неполного класса уравнений, каждый с их соответствующими перечнями решения и каждый соответствует предпочтительному варианту осуществления настоящего изобретения.
Подробное описание предпочтительного варианта осуществления изобретения
Как упоминалось выше, уравнение может иметь следующие состояния: нерешаемое (неизвестны более одной переменной в уравнении), решаемое (неизвестна только одна переменная в уравнении) или избыточное (известна каждая переменная в уравнении).
На фиг. 1 показана примерная система обработки 100 согласно настоящему изобретению. Система обработки 100 содержит по меньшей мере одно автоматическое рабочее место или устройство, обслуживающее пользователя, или ПВМ (персональную вычислительную машину) 110 (далее для простоты называемую только автоматизированным рабочим местом 110) и/или по меньшей мере одну универсальную вычислительную машину 120. Поскольку точный состав автоматизированных рабочих мест и вычислительных машин хорошо известен, их описание здесь не приводится.
Имеется система компьютерного проектирования (КП) для пользователя, которая также хорошо известна в технике, типа коммерческой готовой к непосредственному использованию системы компьютерного проектирования и изготовления, подобной системе Униграфикс (зарегистрированная торговая марка и продукция корпорации "Электроник дейта системс"), постоянно находящейся на рабочем месте (АРМ) 110 и/или в вычислительной машине 120, в зависимости от конкретной конфигурации системы обработки 100. Такая система АП включает устройство для составления эскизов уравнений системы и может создавать двухмерные чертежи и/или трехмерные пространственные модели.
Вначале пользователь вводит геометрические и габаритные ограничения в устройство определения уравнений 160 с целью определения ряда соотношений, формирующих подлежащий моделированию требуемый объект. Эти входные данные обычно бывают в форме уравнений. Система КП (компьютерного проектирования) предписывает системе обработки 100 обратиться в запоминающее устройство 130 через шину 140 для передачи в систему 150 устройства составления эскиза. На основании принятых входных данных система 150 устройства составления эскиза делает логический вывод в устройстве определения уравнений 160 о некоторых геометрических и/или габаритных соотношениях также в форме уравнений, определяющих взаимосвязи между переменными. Таким образом, система 150 устройства составления эскиза создает все уравнения, необходимые для определения профиля посредством устройства определения уравнений 160 либо путем учета геометрической формы, либо посредством принятия ограниченных входных данных. Пользователь не имеет дела с уравнениями, предназначенными непосредственно для определения; эти уравнения (аксиомные, а также выведенные системой) понятны для пользователя. Все релевантные уравнения затем передаются в схему присваивания приоритетов уравнений 165, которая располагает уравнения в соответствии с приоритетом и передает расположенные в соответствии с приоритетом уравнения в устройство сортировки уравнений 170, предназначенное для сортировки. После сортировки уравнений они далее решаются решающим устройством уравнений 175, которое создает профиль нужного объекта в качестве выходных данных, подаваемых на генератор эскизов 180 или на прикладные системы 190, 192, 194 для дальнейшей обработки. Генератор эскизов 180 системы 150 устройства для составления эскизов использует профиль для создания эскиза нужной модели. Этот эскиз можно выводить на автоматизированное рабочее место (АРМ) 110 и/или вычислительную машину 120, или его можно подавать в прикладные системы 190, 192, 194 для дополнительной обработки. Редактор уравнений 185 дает возможность пользователю изменять одно или больше ограничений профиля посредством шины 140 от АРМ 110 и/или вычислительной машины 120. Такие изменения осуществляются в устройстве 175 решения уравнений, которое решает соответствующие уравнения и создает на их основе новые профили.
На фиг. 2 изображена блок-схема предпочтительного варианта осуществления изобретения. В блоке 200 система принимает все определенные пользователем входные данные, обычно в форме уравнений, содержащих геометрические и/или габаритные ограничения. После того, как система приняла такие определенные пользователем входные данные, она предпочтительно вырабатывает в ответ аксиомные и полученные в результате заключения системой уравнения в блоке 210. После того, как система завершит вырабатывание этих уравнений, присущих определению требуемого геометрического объекта, подлежащего моделированию, система собирает определенные пользователем входные данные и вырабатываемые системой уравнения в единую систему подлежащих решению уравнений.
В соответствии с настоящим изобретением система подлежащих решению уравнений предпочтительно сначала располагается в соответствии с приоритетом в блоке 220. Для расположения уравнений в соответствии с приоритетом решения используемые для описания геометрической конфигурации модели уравнения делятся на классы: аксиомные уравнения, определяемые пользователем уравнения и выводимые системой уравнения.
Аксиомные уравнения представляют собой фундаментальные уравнения, присущие геометрической форме, которую они описывают, они всегда истинные и определяют специфическую геометрическую форму, такую как дуга, окружность, линия и тому подобное. Определяемые уравнения являются уравнениями, предписываемыми пользователем. В качестве примеров, определяемых пользователем уравнений, следует указать точно определенные градусы измерений, или две переменные представляют точно установленное расстояние, или две дуги имеют один и тот же радиус, за исключением того, что одна на три дюйма (7,62 см) короче по длине, чем другая и т.д. Следует понимать, что как аксиомный, так и определяемый пользователем классы уравнений описывают геометрические ограничивающие условия, например параллельные линии, или размерные ограничивающие условия, например радиальный размер. Выводимые системой уравнения представляют собой геометрические ограничения, которые выводит вычислительная система. Например, если начерченные линии примерно одной длины, система делает вывод, что линии одной и той же длины.
Аксиомные уравнения соответствуют предпочтительному состоянию классу - 0, а выводимые пользователем уравнения и выводимые системой уравнения можно найти в классе - 1 и классе - 2 соответственно. В соответствии с предпочтительным вариантом осуществления настоящего изобретения эти уравнения геометрических конфигураций решаются в следующем порядке: класс = 0, затем класс = 1, и наконец, класс = 2, если нужно получить требуемую геометрическую конфигурацию.
Главная выгода, получаемая в результате расположения уравнений в соответствии с порядком, заключается в том, что определяемые пользователем уравнения предшествуют уравнениям, выводимым системой. Например, если пользователь начертил две окружности с почти равными радиусами, то система делает вывод, что радиусы действительно равны. Если пользователь, кроме того, определил, что радиус одной окружности на два дюйма (5,08 см) меньше, чем радиус другой окружности, определяемое системой ограничение, состоящее в том, что радиусы равны, будет игнорировано системой, когда она позже будет создавать геометрическую модель.
В качестве предварительной обработки для решающего устройства система уравнений, связанных с эскизом, переупорядочивается, а отдельные уравнения перезаписываются в такой форме, что их можно решить по отдельности. Этот процесс называется сортированием уравнений, что осуществляется в блоке 230, и в нем используется следующая система обозначений для системы уравнений:
1 (Vi (a), Vj (b), ...);
2 (Vk (c), Vl (d), ...);
3 (Vm (e), Vn (f), ...),
где: a, b, c, d, e, f - полные числа (в частности, 1, 2 или 3), а Vi, Vj и т.д. - переменные, связанные с эскизом.
Упорядоченный (связный) список решаемых уравнений (далее называемый списком решаемых уравнений) построен с использованием критериев, в соответствии с которыми в перечень можно добавлять уравнение, если единственная переменная в уравнении может быть изолирована. Устройство сортировки уравнений останавливается, когда оказывается невозможно добавить в перечень решаемых уравнений другое уравнение. Способность сортировки согласно изобретению лучше описывается с помощью следующего примерного символического кода:
10 continue (продолжение)
Цикл по уравнениям, еще не попавшим в перечень
Если уравнение имеет только одну неизвестную, и уравнение можно переписать так, что единственная неизвестная изолируется, тогда уравнение переписывается и вводится в решаемый перечень.
Конец цикла
Если в течение последнего цикла было введено по меньшей мере одно уравнение,
then (тогда) перейти к 10
else (еще) (продолжать)
endif (закончить, если)
Процесс сортировки завершен.
Благодаря процессу сортировки уравнений, настоящее изобретение создает список решаемых уравнений, который является ориентированным ациклическим графом, устанавливающим соотношение характеристических данных геометрической формы с характеристическими данными другой геометрической формы. Аксиомные уравнения гарантируют, что для нахождения в списке решаемых уравнений необходимо только минимальное количество данных, чтобы "знать" сущность геометрической формы. Любая переменная, которая не изолирована в уравнении в перечне, является "неизвестной". Если неизвестных переменных нет, то профиль эскиза является "полностью ограниченным", в другом случае профиль эскиза является "неограниченным".
Перечень решаемых уравнений получается путем прохода первого цикла по отдельным уравнениям в пределах класса уравнений. Следует понимать, что циклическое прохождение относится к соответствующей настоящему изобретению системе, проходящей по каждому из уравнений в классе до тех пор, пока система не добавит все уравнения, имеющие только одну неизвестную переменную, к перечню решаемых уравнений, прежде чем перейти к следующему классу.
Обычно соответствующая настоящему изобретению система проходит по уравнениям класса = 0 до тех пор, пока все решаемые уравнения не переместятся в перечень решаемых уравнений, оставляя какое-то количество оставшихся нерешаемых уравнений для более позднего рассмотрения. Затем система переходит к классу = 1 и опять переносит все решаемые уравнения в решаемый перечень, снова пропуская нерешаемые уравнения в классе. В момент, когда система переместит самое первое выведенное системой уравнение в класс = 2 в перечень решаемых уравнений, система сразу же возвращается к оставшимся уравнениям в классе = 0. Система циклами проходит по классу, отыскивая следующие решаемые уравнения для того, чтобы добавить их к перечню решаемых уравнений теперь, когда другие уравнения добавлены к перечню решаемых уравнений. Система циклически проходит по классу = 0 до тех пор, пока не останется больше уравнений, которые можно было бы добавить к перечню решаемых уравнений, и затем переходит к циклическому прохождению по уравнениям класса = 1 до тех пор, пока не останется больше уравнений, которые можно было бы добавить к решаемому перечню. В это время система переходит к классу = 2 и проходит по выводимым системой уравнениям до тех пор, пока не найдет уравнение, которое можно перенести в решаемый список, после чего она сразу возвращается к оставшемуся набору уравнений класса = 0, и процесс повторяется. Этот процесс продолжается до тех пор, пока все уравнения, которые можно решить, независимо от класса и исключая избыточные уравнения, как описано ниже, не будут перемещены в перечень решаемых уравнений.
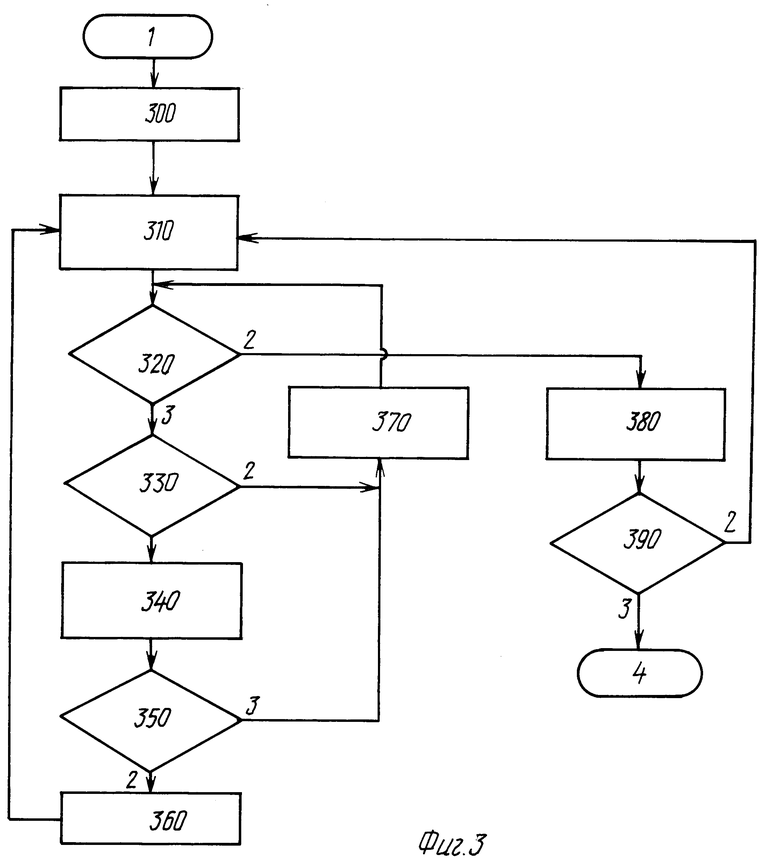
На фиг. 3 более подробно показана блок-схема части уравнений сортировки, показанной на фиг. 2, в соответствии с предпочтительным вариантом осуществления настоящего изобретения. В блоке 300 система начинает с уравнений (аксиомных) класса = 0. В блоке 310 она получает первое уравнение в классе. Если в нулевом классе имеется уравнение в блоке решения 320, настоящая система определяет, одна ли только неизвестная имеется в уравнении в блоке решения 330. Если нет, то система пропускает это уравнение, принимает следующее уравнение в блоке 370 и возвращается к блоку решения 320. Если уравнение имеет только одну неизвестную, уравнение добавляется к перечню решаемых уравнений в блоке 340. В блоке решения 350 система проверяет, находится ли она еще в нулевом или в первом классе. Если так, то она переходит к блоку 370 для рассмотрения следующего уравнения.
Если нет уравнения или нет следующего уравнения в аксиомном классе, система перейдет к блоку 380, где счетчик классов получает приращение. В блоке решений 390 система определяет, закончилась ли обработка всех классов. Если да, то она переходит к блоку 290, где система решает сортированные уравнения. Однако в настоящем примере система не заканчивает процесс и переходит к получению первого уравнения в следующем классе, класс = 1. Система вновь продолжает проверять каждое уравнение, чтобы обнаружить уравнения только с одной неизвестной, переводя те из них, которые готовы к переводу в решаемый перечень. После того, как система циклически пройдет по всем уравнениям в классе = 1, она переходит в блок 380 для обеспечения приращения счетчика классов, определения, закончен ли этот класс (в данном случае - нет) и переходит к получению первого уравнения из класса = 2.
После циклического прохождения уравнений в пределах класса = 2 до тех пор, пока она находит уравнение только с одной неизвестной, и добавляет его к решаемому перечню, система устанавливает, находится ли она в классе = 2. Она устанавливает счетчик классов на класс = 0 и возвращается для проверки уравнений, которые она первоначально пропустила в аксиомном классе, чтобы определить, содержат ли теперь какие-нибудь из них только одну неизвестную как результат уравнений, находящихся в данный момент в списке решаемых уравнений. Как и прежде, система циклически проходит по системам уравнений класса = 0 и класса = 1, прежде чем возвратиться к классу = 2. Каждый раз, когда система помещает уравнение класса = 2 в перечень решаемых уравнений, она сразу возвращается к уравнениям класса = 0 и класса = 1 для того, чтобы посмотреть, можно ли какое-либо из оставшихся уравнений в этих классах теперь переместить в решаемый перечень. Этот процесс продолжается до тех пор, пока не будут перенесены все уравнения, которые можно перенести в решаемый перечень.
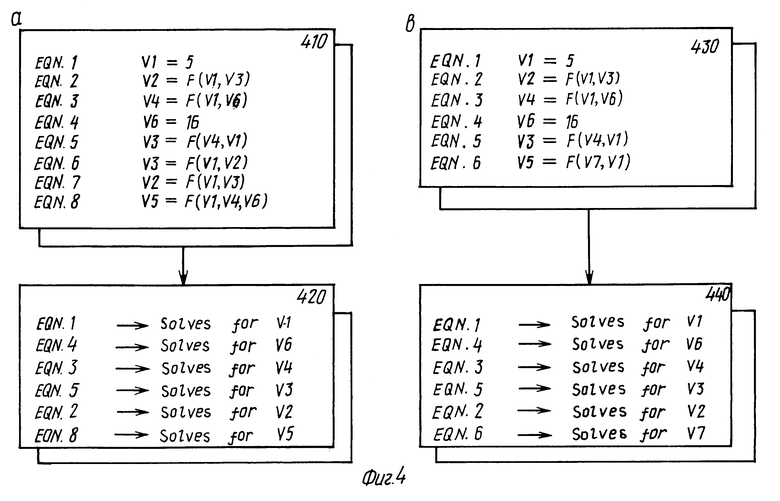
Фиг. 4A схематически иллюстрирует пример переполненной системы уравнений 410 вместе с ее соответственным списком решаемых уравнений 420 согласно предпочтительному варианту осуществления настоящего изобретения. Допустим, что такая система уравнений расположена в соответствии с приоритетом и включает все классы уравнений, включая аксиомные, выводимые системой и определяемые пользователем уравнения. Следует понимать, что порядок в пределах классов этих уравнений не важен. Система оценивает каждое уравнение набора 410. Если уравнение имеет только одну неизвестную, оно добавляется к перечню решаемых уравнений 420, который является упорядоченным перечнем уравнений, используемых для определения геометрической формы модели. Если уравнение имеет более одной неизвестной, уравнение пропускается, а система приступает к оценке следующего уравнения.
На фиг. 4a первое уравнение имеет одну неизвестную, поэтому система автоматически помещает первое уравнение в список решаемых уравнений 420 и показывает, что первое уравнение может быть решено в отношении одной переменной. Система переходит к уравнению два. Поскольку уравнение два имеет две неизвестные, система пропускает уравнение два, оставляя его в списке нерешаемых уравнений 410. Система переходит к следующему уравнению. Уравнение три имеет две неизвестные, так что система также пропускает уравнение три. Четвертое уравнение в списке имеет одну неизвестную (обозначенную переменной шесть), так что система добавляет уравнение четыре к перечню решаемых уравнений 420. Уравнение пять также имеет две неизвестные величины, таким образом система пропускает уравнение пять. Этот процесс продолжается до тех пор, пока система не достигнет упорядоченного перечня, то есть перечня решаемых уравнений 420.
Хотя уравнения шесть и семь являются решаемыми уравнениями, в то же время они являются избыточными уравнениями. Любое уравнение, не содержащее неизвестных переменных, рассматривается как "избыточное" и не переносится в перечень решаемых уравнений. Поэтому система определяет уравнение шесть и семь как избыточные уравнения в блок решения 240 (фиг. 2) и добавляет их к перечню избыточных уравнений в блок 250 вместо перечня решаемых уравнений 420, и этот перечень избыточных уравнений отделяется в сторону для обработки после окончания сортирования. Поскольку все переменные уже известны из уравнений в перечне решаемых уравнений 420, избыточные уравнения не используются, а это означает, что система уравнений 410 является примером переполненной системы уравнений.
До создания настоящего изобретения система, решающая эскизы, не могла продолжать обработку, если имелись избыточные уравнения, и такая система не могла просто не принимать в расчет избыточные уравнения. Это происходило потому, что в отличие от соответствующей настоящему изобретению системы такие системы не могут определять, какие уравнения являются избыточными, или сообщать пользователю о наличии и влиянии таких избыточных уравнений в системе.
В системе предпочтительно используются некоторые избыточные уравнения для двойной возможной проверки, что значения в перечне решаемых уравнений точные или что нет конфликтов между уравнениями. Для этого берется каждое избыточное уравнение и вставляется во все кроме одного значения вместо переменной. Поэтому, в данном примере найденные значения шесть из перечня решаемых уравнений подставляются в уравнение для того, чтобы посмотреть, является ли значение, полученное для переменной V3, таким же при использовании уравнения шесть, какое обеспечивает уравнение пять.
Если каждое избыточное уравнение дает значение, которое соответствует решаемому значению, система уравнений считается полностью определенной или "связанной". С другой стороны, избыточное уравнение считается "конфликтным", если значение, полученное из уравнения из перечня решаемых уравнений, не такое, как полученное из избыточного уравнения для той же самой переменной. Следовательно, если система установила, что имеется конфликтная информация из-за использования избыточного уравнения (уравнений) этим способом, система после этого выясняет, имеется ли конфликтная информация между определяемыми пользователем уравнениями или между определяемым пользователем уравнением и выводимым системой уравнением. Иллюстрацией первого могло бы быть, если пользователь определяет радиус дуги два в виде удвоенного радиуса дуги один в одном уравнении и определяет отношение радиусов в виде 3:1 в другом уравнении. В этой ситуации одно из уравнений может быть в избыточном списке и может подходить с другим значением, чем уравнение в перечне решаемых уравнений. Затем система обеспечивает сообщение пользователю, что эти уравнения конфликтные, и представляет особые конфликтные уравнения.
Однако, если имеется конфликт между определяемым пользователем уравнением и выведенным системой уравнением, система просто стирает выведенное системой избыточное уравнение. Например, пользователь начертил дуги почти равными радиусами, поэтому система заключает, что радиусы одинаковые. Однако пользователь в действительности определил радиус дуги два как удвоенный радиус дуги один. Поэтому, чтобы пользователь получил то, что он имел в виду, выведенное системой избыточное уравнение стирается. Система не вырабатывает сообщение, отражающее конфликт, поскольку пользователь никогда не определял дуги равными.
Рассмотрим теперь фиг. 4b, которая схематически иллюстрирует примерный неполный набор уравнений 430 вместе с его списком решаемых уравнений 440 согласно предпочтительному варианту осуществления изобретения. Предположим, что такой набор уравнений 430 расположен в соответствии с приоритетом и включает в себя все классы уравнений, включая аксиомные, выведенные системой и определяемые пользователем уравнения. Как и в примере, показанном на фиг. 4a, порядок в пределах классов этих уравнений не имеет значения.
На фиг. 4b система выполняет такой же процесс, что описан для фиг. 4a. Однако в этом примере уравнение шесть остается нерешаемым, тогда как уравнения с первого по пятое переносятся в перечень решаемых уравнений 440. Уравнение шесть устанавливает, что переменная V5 является функцией переменных V7 и V1. Хотя система знает, что значение, предназначенное для присваивания переменной V1, основано на содержимом перечня решаемых уравнений, и знает значения для переменных V1, V2, V3, V4 и V6, система определяет, что значения переменных V5 и V7 не известны, и поэтому уравнение шесть нерешаемое (фиг. 2, блок решения 260).
Затем система предпочтительно фиксирует одну из неизвестных в блоке 270 (фиг. 2) в соответствии с перечисленной ниже предпочтительной эвристикой, давая переменной значение, которое пользователь начертил на экране. Предположим, что эта эвристика предписывает системе присвоить такое значение переменной V5. После этого система решает уравнение шесть для того, чтобы найти значение для переменной V7 и перевести уравнение шесть в список решенных уравнений. Уравнение шесть теперь считается дополнительным уравнением. Таким образом, в случае неполной системы уравнений эвристика устройства автоограничения (которая является частью соответствующего настоящему изобретению устройства решения уравнений) предписывает системе интеллектуально и автоматически ограничить достаточное количество переменных для того, чтобы усилить решение всех уравнений, обеспеченных для участка сортирования настоящей системы, и обеспечить тем самым возможность перевести все неизбыточные уравнения в перечень решаемых уравнений. Следует понимать, что хотя в примере показано только одно недостаточное уравнение, если здесь будет два или более таких уравнений, система устанавливает одну переменную и возвращается к сортированию и циклическому прохождению по оставшимся недостаточным уравнениям для того, чтобы определить, решаемы ли они теперь или нет.
Участок устройства автоограничения настоящего изобретения является расширением устройства решения уравнений, которое дает возможность устройству решения уравнений определять некомплексный корень для системы неполных алгебраических уравнений. Дополнительные уравнения выбираются с использованием набора эвристики, который учитывает геометрическую форму, описанную первоначальной системой уравнений. Это происходит потому, что дополнительные уравнения имеют следующие желательные характеристики: они не конфликтуют с уравнениями, которые уже находятся в системе (например, решение для дополнительного уравнения оказывается в области решений первоначальной системы уравнений) и они естественно развязаны с любым уравнением в первоначальной системе уравнений, т.е. их можно решать без знания первоначальной системы уравнений. Эти характеристики дали возможность эвристике развиться так, чтобы создать полностью заполненную систему уравнений, которая дает соответствующее и желательное решение для первоначальной системы уравнений.
Следует отметить, что хотя показанный на фиг. 4b настоящий пример является лишь неполной системой, в то же время система уравнений может иметь избыточные уравнения и быть неполной. Это означает, что некоторые переменные известны из более чем одного уравнения, в то время как другие переменные остаются неизвестными. Соответствующая настоящему изобретению система адресует обе эти ситуации, даже когда они имеют место в одной и той же системе уравнений. Однако для облегчения понимания на фиг. 4a и 4b в данном случае две ситуации показаны отдельно.
Кроме того, следует понимать, что хотя все уравнения находятся в перечне решаемых уравнений, в случае неполной системы уравнений перечень решаемых уравнений никогда не имеет завершенной (полностью заполненной) системы решений. Из рассмотрения данного примера (фиг. 4b) видно, что перечень решаемых уравнений 440 не имеет решаемого уравнения для переменной V5. Более того, как описано выше, перечень решаемых уравнений является упорядоченным связанным списком уравнений, используемых для определения геометрической формы нужного объекта, которая используется системой для установления профиля эскиза, даже несмотря на то, что в данном случае это неполный список решаемых уравнений.
Устройство автоограничения применяет эвристику для выяснения, какие неизвестные переменные зафиксировать при условии, что система уравнений неполная. Система предпочтительно присваивает значения неизвестным переменным в оставшихся неизвестных уравнениях в следующем порядке: сначала неизвестным переменным углов линий, затем неизвестным переменным радиусов дуг, за которыми следуют неизвестные переменные длин линий. Потому система присваивает значения неизвестным переменным углов дуг, после чего неизвестным переменным конечных точек линий, за которыми следуют неизвестные переменные центров дуг и, наконец, неизвестные переменные конечных точек пазов и конусов. Следует понимать, что система предпочтительно присваивает значения неизвестным переменным в каждом типе переменных до перехода к следующему типу. Например, если остались две неизвестные переменные углов линий и неизвестная переменная радиуса дуги, система предпочтительно присвоит значения обоим переменным углов линий прежде, чем присваивать значение неизвестной переменной радиуса дуги.
До настоящего изобретения решающая программа для эскизов была неспособна найти какое-нибудь решение неполной системы уравнений. Это обязывало запрашивать больше информации у пользователя. Настоящее изобретение не только находит решение для такой системы уравнений, но поскольку оно использует интеллектуальную эвристику для решения, какие переменные фиксировать, оно обычно находит действительный корень, который имеется в системе уравнений, в противоположность корню, который может быть комплексным.
Может случиться, что система не выдает результаты, которые ожидает пользователь. Примером такой ситуации может быть случай, если пользователь только начертил линии и если система абсолютно не обеспечена уравнениями (геометрические соотношения или ограничения). В такой ситуации система только фиксирует все точки и отобразит чертеж, как начертил его пользователь. Таким образом, никогда не произойдет так, что система не сможет решить систему уравнений.
После того, как соответствующие настоящему изобретению система и способ завершат сортирование уравнений и создадут упорядоченный перечень решаемых уравнений в блоке 280, она решает уравнения в списке решаемых уравнений относительно их соответственных переменных в блоке 290. Уравнения предпочтительно решаются непосредственно после их сортирования. В частности, определяется значение для неизвестной переменной в каждом решаемом уравнении, и эти найденные значения переменных формирует профиль, который используется для получения геометрической конфигурации модели. Список решаемых уравнений не имеет большого значения, пока решаются уравнения относительно их неизвестных переменных. Следовательно, используя примеры либо фиг. 4a, либо фиг. 4b, система начинает с уравнения один, которое устанавливает переменную V1, равной 5. Система устанавливает или фиксирует V1 = 5. Затем система переходит к решению в отношении переменной V6. Следует помнить, что каждая размерная переменная имеет три связанных с ней координаты, так что она оказывается точкой (x, y, z). В данном объяснении в целях его упрощения используется только одна координата в уравнениях, независимо от типа переменной. Система продолжает проходить по списку решаемых уравнений, и поскольку это упорядоченный список, система знает, какое уравнение считывать и решать следующим. Таким образом, используя установленное значение переменной V1, система решает четвертое уравнение и устанавливает переменную V6, равную 16. Как указано выше, все выведенные системой избыточные уравнения предпочтительно стираются.
Часто подлежащее решению уравнение имеет больше одного действительного корня. Когда это происходит, используется эвристика для решения, какой нужно выбрать корень при решении уравнения. Эвристика основана на местоположении и конфигурации геометрической формы в то время, когда активизируется соответствующая настоящему изобретению способность решения уравнений.
После завершения упорядоченных уравнений в блоке 290 система корректирует переменные, поправляет геометрическую форму профиля эскиза и восстанавливает связанные объекты. Характеристические данные геометрической формы реконструируются по новым значениям связанных переменных эскиза, включая избыточные уравнения ограничения.
После того, как система завершит свой процесс обработки уравнений, определяющих требуемую геометрическую модель, в блок 290, полученный профиль можно выводить на автоматизированное рабочее место 110 и/или вычислительную машину 120, а также на прикладные задачи 190, 192, 194 (фиг. 1). Прикладными задачами 190, 192, 194 могут быть, например, двухмерные или трехмерные задачи геометрического моделирования, использующие профили.
Допустим, пользователю нужно отредактировать параметр в профиле, полученном согласно настоящему изобретению. До настоящего изобретения если необходимо было изменить деталь, пользователь должен был стереть, а затем вновь создать поврежденную геометрическую форму. В случае настоящего изобретения пользователю необходимо только отредактировать нужное ограничение, и система автоматически повторно решит все из затронутых уравнений гораздо быстрее, чем прежние системы. Это происходит потому, что сортирование в блоке 230 производится только тогда, когда добавляются или стираются уравнения. Если пользователь только изменил значения переменных, система предпочтительно не пересортировывает все уравнения, а вместо этого просто повторно решает перечень решаемых уравнений. Например, если пользователь редактирует V1 уравнения один, делая его равным 6 вместо 5, настоящая система корректирует соответствующие уравнения в перечне решаемых уравнений, подвергая их такому изменению, и выполняет другой кодовый профиль. На основании этого профиля система вновь создает новое графическое представление требуемой геометрической модели. Специалистам в данной области техники будет очевидно, что настоящее изобретение можно также использовать в других областях. Например, его можно непосредственно применять для решения задач пространственных геометрических профилей (в противоположность решению проекций пространственных геометрических профилей на двухмерную плоскость). Настоящее изобретение можно применять также для решения системы алгебраических уравнений, описывающих системы, отличающиеся от геометрических профилей объектов. Один способ осуществления этого может заключаться в замене эвристики, используемой для создания дополнительных уравнений, модифицируя таким образом аспект автоограничения настоящего изобретения для дополнения систем уравнений, чтобы представлять системы, отличающиеся от механических конструкций. Далее, с помощью изменения входных данных для алгебраических уравнений, т.е. изменения коэффициентов и постоянных в системе уравнений, система и способ могут использоваться для решения вероятностных проблем механики, или проблем наложения с допуском, или даже для работы в качестве части алгоритма Монте-Карло.
Специалисты в данной области техники понимают, что это описание представлено только в качестве иллюстративного примера и ни в коем случае его нельзя рассматривать ограничением описываемого здесь изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОМПЬЮТЕРНОГО УПРАВЛЕНИЯ ПОСТРОЕНИЕМ ИЗДЕЛИЙ | 1994 |
|
RU2119188C1 |
| СИСТЕМА И СПОСОБ ЭЛЕКТРОННОГО ПЕРЕЧИСЛЕНИЯ ФОНДОВ ПОСРЕДСТВОМ АВТОМАТИЗИРОВАННОГО КАССОВОГО АППАРАТА ДЛЯ ВЫДАЧИ ПЕРЕВОДИМЫХ ФОНДОВ | 1996 |
|
RU2172022C2 |
| ДИНАМИЧЕСКАЯ ЭКСПЕРТНАЯ СИСТЕМА | 2011 |
|
RU2462752C1 |
| НАСТРАИВАЕМЫЕ ТАБЛИЧНЫЕ СТИЛИ ДИНАМИЧЕСКИХ ТАБЛИЦ | 2006 |
|
RU2419851C2 |
| СЕТЬ ДЛЯ ОБЕСПЕЧЕНИЯ ЧУВСТВИТЕЛЬНОСТИ, ДВУСТОРОННЕЙ СВЯЗИ И УПРАВЛЕНИЯ | 1988 |
|
RU2090926C1 |
| АНАЛИТИЧЕСКИЕ МОДЕЛИ КАРТЫ | 2009 |
|
RU2497188C2 |
| СИСТЕМА И СПОСОБ УСТАНОВКИ И ВЫПОЛНЕНИЯ ПРИКЛАДНЫХ ПРОГРАММ ПРЕДПОЧТЕНИЙ | 2004 |
|
RU2364917C2 |
| СИСТЕМЫ И СПОСОБЫ СОПРЯЖЕНИЯ ПРИКЛАДНЫХ ПРОГРАММ С ПЛАТФОРМОЙ ХРАНЕНИЯ НА ОСНОВЕ СТАТЕЙ | 2003 |
|
RU2412461C2 |
| СИСТЕМА И СПОСОБ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕКЛЮЧЕНИЯ ПРИ НЕОПТИМАЛЬНОСТИ ЦЕЛЕВОГО ОБЪЕКТА НАЗАД И ПРИОРИТЕТА ЦЕЛЕВОГО ОБЪЕКТА ДЛЯ РАСПРЕДЕЛЕННОЙ ФАЙЛОВОЙ СИСТЕМЫ | 2005 |
|
RU2406123C2 |
| ИСПОЛЬЗОВАНИЕ ПРИБЛИЖЕННОГО МЕСТОПОЛОЖЕНИЯ УСТРОЙСТВА, ОПРЕДЕЛЕННОГО НА ОСНОВАНИИ ВНЕШНИХ СИГНАЛОВ | 2004 |
|
RU2356091C2 |

Изобретения относятся к области компьютерного проектирования и могут быть использованы для параметрического геометрического моделирования объекта. Техническим результатом является повышение точности воспроизводимого профиля. Согласно системе и способу для создания параметрического профиля подлежащего моделированию объекта при помощи соответствующих средств принимают входные данные от пользователя в форме уравнений, вырабатывают дополнительные уравнения, свойственные определению профиля, располагают уравнения в соответствии с приоритетом по ранжированным классам, сортируют расположенные в соответствии с приоритетом уравнения, создавая тем самым упорядоченный список решаемых уравнений, решают сортированные уравнения в том порядке, в каком они находятся в списке решаемых уравнений, и создают профиль геометрических объектов, построенных на основании решений решаемых уравнений. Система и способ автоматически ограничивают неизвестные переменные в любой используемой системе уравнений, основываясь на эвристике и используя некоторые избыточные уравнения для определения и разрешения конфликтов между подлежащими использованию уравнениями для создания профиля. 2 с. и 15 з.п.ф-лы, 4 ил.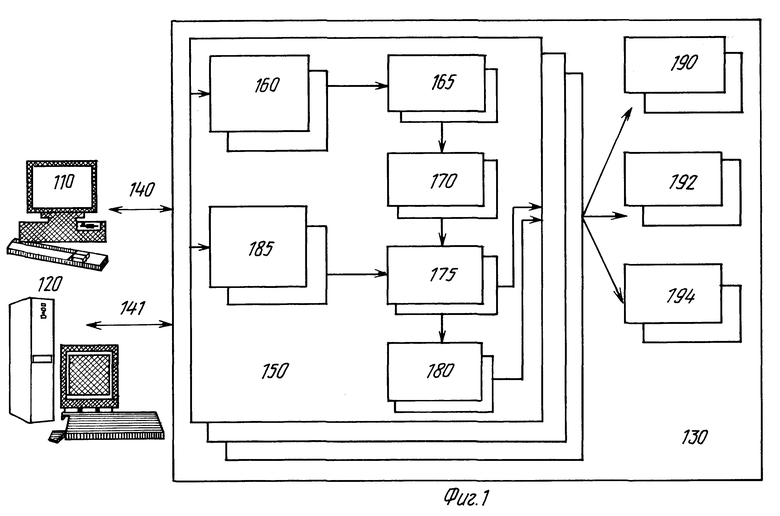
| Способ приготовления консистентных мазей | 1919 |
|
SU1990A1 |
| РЕЛЬСОВАЯ ПЕДАЛЬ | 1920 |
|
SU289A1 |
| INTERNHTIONAL JOURNAL OF SYSTEMS | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Печь для сжигания твердых и жидких нечистот | 1920 |
|
SU17A1 |
| Нефтяной конвертер | 1922 |
|
SU64A1 |
Авторы
Даты
1999-03-10—Публикация
1994-06-20—Подача