Изобретение относится к области автоматики и может быть применено при управлении динамическими объектами с одним входом и одним выходом.
Наиболее близкой к изобретению по совокупности признаков (прототип) является адаптивная система управления с переменной структурой [1], содержащая задатчик, выходом подключенный к входам эталонной модели, первому блоку релейных элементов и сигнальному входу первого масштабирующего усилителя с переменным коэффициентом, измеритель рассогласования, первым входом подключенный к выходу эталонной модели, вторым входом связанный с выходом объекта управления, входом второго блока релейных элементов и сигнальным входом второго масштабирующего усилителя с переменным коэффициентом, а выходом - со входами блока формирования коэффициентом усиления, третьего блока релейных элементов и управляющим входом третьего масштабирующего усилителя с переменным коэффициентом, четвертый блок релейных элементов, вход которого подключен к выходу блока формирования коэффициентов усиления, а выход - к первым входам первого, второго, третьего и четвертого блоков умножителей, вторые входы которых подключены соответственно к выходам первого, второго, третьего и пятого блоков релейных элементов, выходы первого, второго, третьего и четвертого блоков умножителей связаны соответственно с управляющими входами первого, второго, третьего и четвертого масштабирующих усилителей с переменным коэффициентом, выходы которых подключены соответственно к первому, второму, третьему и четвертому входам сумматора, выход сумматора связан с входом объекта управления и формирующим фильтром, соединенным с входом пятого блока релейных элементов и сигнальным входом четвертого масштабирующего усилителя с переменным коэффициентом.
Однако в этой системе при использовании инерционного привода возникают очень большие трудности с сохранением устойчивого скользящего режима.
Цель изобретения - расширение области применения системы за счет возможности и использования в ней инерционного привода.
Эта цель достигается введением в адаптивную систему управления с переменной структурой первого блока четырехполюсника, вход которого подключен к выходу задатчика входного сигнала, а выход - к входу эталонной модели и второго блока четырехполюсника, вход которого связан с выходом сумматора, а выход - с входом объекта управления.
Блок-схема адаптивной системы управления (фиг. 1) содержит задатчик 1 входного сигнала, первый 2, второй 21 блоки четырехполюсников, эталонную модель 3, формирующий фильтр 4, измеритель 5 рассогласования, блок 6 формирования коэффициентов усиления, первый 7, второй 8, третий 9, четвертый 10 и пятый 11 блоки релейных элементов, первый 12, второй 13, третий 14 и четвертый 15 блоки умножителей, первый 16, второй 17, третий 18 и четвертый 19 масштабирующие усилители с переменным коэффициентом, сумматор 20 и объект управления 22.
Известен один из возможных принципов построения адаптивной системы управления для линейного объекта: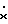 = Ax+Bu, (1)
= Ax+Bu, (1)
основанный на использовании эталонной модели (ЭМ)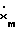 = Aмxм + Bмuз, (2)
= Aмxм + Bмuз, (2)
где x, xм, u, uз - векторы состояния OУ (n•1), ЭМ (n•1), управления (k= 1) и задающих воздействий (m•1) соответственно; A, Aм, B, Bм - матрицы соответствующих размерностей.
Управление выбирается так, чтобы ошибка e=xм-x была сведена к нулю. Для решения этой задачи используется уравнение движения относительно ошибки, получаемое из уравнений (1) и (2), т.е.
 = Aмe + (Aм-A)х + Bмuз-Bu. (3)
= Aмe + (Aм-A)х + Bмuз-Bu. (3)
Для обеспечения устойчивого скользящего режима по пересечению плоскостей скольжения
S=Cтe, (4)
где C - матрица (n•k), S - вектор (k•1), управление определяется из системы неравенств таким образом, чтобы условия существования устойчивого скользящего режима выполнялись во всем диапазоне изменения параметров объекта управления (OУ).
Если выполнены следующие условия:
1) пара матриц /A, B/ управляема;
2) det(CеB) ≠ 0; (5)
3) rank B=rank[B/Bм]=rank[B/Bм], (6)
то движение в скользящем режиме описывается уравнением =[E-B(CтB)-1Cт]Aмe, (7)
=[E-B(CтB)-1Cт]Aмe, (7)
т. е. не зависит ни от коэффициентов матрицы A, ни от задающего воздействия uз. Однако необходимость выполнения условий является серьезным препятствием при создании подобных адаптивных систем. Кроме того, вектор x должен быть непосредственно наблюдаем, иначе необходимо дополнительно синтезировать устройство оценивания вектора состояния, что требует решения задачи текущей идентификации. Отмеченные трудности легко преодолеваются, если при синтезе использовать неминимальную форму (НМФ) модели OУ.
Пусть динамические свойства линейного стационарного объекта управления с одним входом и одним выходом Z описываются передаточной функцией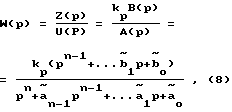
в котором нет сокращаемых нулей и полюсов. Разделим числитель и знаменатель функции (1) на устойчивый полином:
β(p) = pn-1+βn-2pn-2+...+β1p+βo
и результат запишем в виде
где ai, bi - коэффициенты, полученные при делении полиномов A(p) и B(p) на полином β(p).
Введем новые переменные:
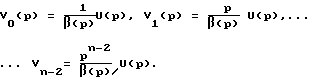
С учетом проведенных преобразований уравнения OУ (1) в пространстве состояний запишутся так: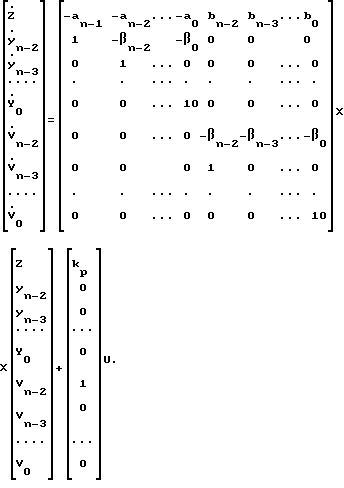 (10)
(10)
Порядок полученной модели равен (2n-1)>n, поэтому она называется неминимальной.
Запишем уравнение OУ (10) в ЭМ в следующем виде: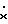 = Ax+Bu+Df, (11)
= Ax+Bu+Df, (11) = Aмхм+Bмuз, (12)
= Aмхм+Bмuз, (12)
где xт=[ZYn-2Yn-3...Y0], x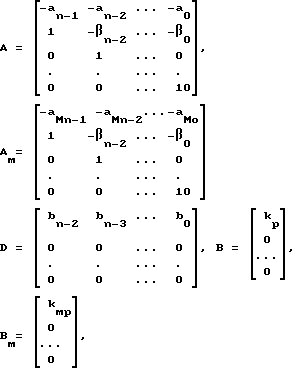
f - вектор, полученный из решения уравнения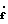 = Ff+Gu, (13)
= Ff+Gu, (13)
где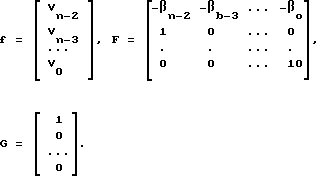
Введя для ЭВМ (12) переменные в виде (9), получим ее передаточную функцию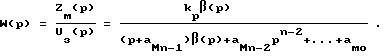
Таким образом, форма (11) ЭМ позволяет задавать желаемую передаточную функцию, у которой порядок полинома числителя на единицу меньше порядка полинома знаменателя и все корни полинома числителя лежат слева от мнимой оси на комплексной плоскости. Последнее условие связано с необходимостью обеспечения устойчивости модели, так как полином β(p), используемый при ее формировании, совпадает с точностью до постоянного множителя с числителем ЭМ.
Для получения уравнения движения относительно ошибки вычтем из уравнения (12) уравнение (11) и после преобразования получим = Aмe+(Aм-A)x+Bмuз-Df-Bu, (14)
= Aмe+(Aм-A)x+Bмuз-Df-Bu, (14)
где eт=[e1e2...en]=[Zм-Z/Yмn-2- Yn-2/Yм0-Y0].
Нетрудно убедиться, что при выбранной структуре модели OУ условия (6) выполняются:
Cт=[1Cn-2Cn-3...C0], (15)
то после преобразований уравнения движения в скользящем режиме принимают вид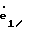 =-(cn-2e2+cn-3e3+... c0en), (16)
=-(cn-2e2+cn-3e3+... c0en), (16)
Таким образом, движение в скользящем режиме не зависит ни от параметров OУ (11): коэффициентов матриц A, B, D, ни от задающего воздействия uз, а целиком определяется заданием параметров плоскости скольжения и числителя ЭМ.
Для обепсечения устойчивости режима скольжения управление должно быть выбрано так, чтобы выполнялось условие 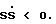
Закон управления будем искать в виде
u = ψ
где элементы векторов ψe,ψx,ψf и скаляр ψu определяются по формулам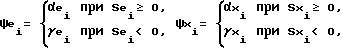
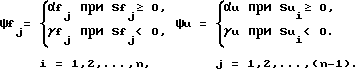
Найдем произведение SS с учетом уравнений (4), (14), (17):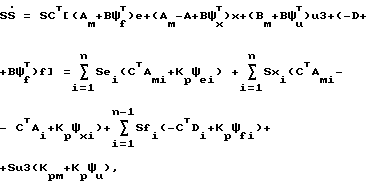
где Ai, Aмi, Di - столбцы матриц A, Aм, D; ei, xi, fi - элементы векторов e, x, f соответственно.
Условие устойчивого скользящего режима SS<0 будет выполняться, если коэффициенты закона управления (17) выбрать из условий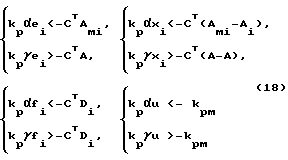
В процессе функционирования OУ изменяются коэффициенты матриц A, B, D. Однако границы их изменения известны и параметры закона управления (17) можно выбрать так, чтобы неравенства (18) соблюдались для всех режимов работы. В этом случае замкнутая система управления (11), (17) в скользящем режиме будет адаптивной, т.е. инвариантной к изменению характеристик OУ и задающего воздействия.
Необходимо также оценить характер изменения вектора f в уравнении (13) при управлении (17), так как при f → ∞ управление Uэкв определяется из уравнения 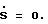 С учетом формул (4), (14) и (15) запишем
С учетом формул (4), (14) и (15) запишем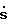 = Cт(Aмe+Aмx-Ax+Bмuз-Df- BUэкв)=0.
= Cт(Aмe+Aмx-Ax+Bмuз-Df- BUэкв)=0.
Определим из этого уравнения
Uэкв=(CтB)-1Cт[Df-Aмe+ (Aм-A)x+Bмuз]
и, подставив его в уравнение (13), получим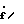 = [F-G(CтB)-1CтD]f+G(CтB)-1 Cт[Aмe+(Aм-A)x+Bмuз,
= [F-G(CтB)-1CтD]f+G(CтB)-1 Cт[Aмe+(Aм-A)x+Bмuз,
или после преобразований с учетом формул (11), (13) и (15)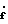 = Rf+Gkp -1 Cт[Aмe+(Aм-A)x+Bмuз],
= Rf+Gkp -1 Cт[Aмe+(Aм-A)x+Bмuз],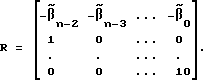
Так как в соответствии с (16) e ---> 0, ЭМ (12) выбирается устойчивой и значение uз ограничено по величине, то и значения компонент вектокра x ---> xм также ограничены. В этом случае значения компонент вектора f ограничены только тогда, когда матрица R - гурвицева. Это значит, что корни числителя передаточной функции (8) OУ должны располагаться слева от мнимой оси комплексной плоскости.
Рассмотрим эффективность предложенной методики на примере синтеза адаптивной системы управления гипотетического самолета с эталонной моделью в продольной плоскости. Уравнения короткопериодического движения самолета и ЭМ в этом случае имеет вид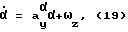
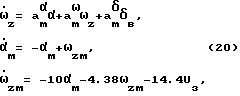
где α,αм - угол атаки, ωz,ωzм - угловая скорость тангажа самолета и ЭМ, δв - отклонение руля высоты самолета, uз - задающее воздействие. Коэффициенты уравнений (19) для двух режимов полета представлены в табл. 1
При исследовании эффективности адаптивной системы будем полагать, что
1) δвз = sint + 1/3sin3t + 1/5sin5t + 1/7sin7t,
2) в качестве цели синтеза адаптивной будем считать выполнение условия 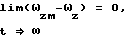
3) привод руля высоты будем описывать дифференциальным уравнением δв= -1/Tδв+1/TU, где T-постоянная времени привода, U - управляющий сигнал.
Из уравнений (19), (20) определяем передаточные функции (ПФ) самолета и ЭМ: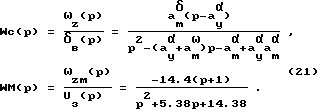
На этапе синтеза будем полагать привод руля высоты безинерционным: δв= U. Полином β(p) принимаем равным числителю Wм(p) β(p) = p+1, а вектор Cт = [1 0]. При сделанных допущениях уравнения (11) - (13) принимают вид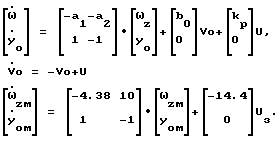
Коэффициенты уравнений (21) для рассматриваемых режимов приведены в табл. 2.
Неравенства (18) запишутся так:
1) для режима N 1:
2) для режима N 2: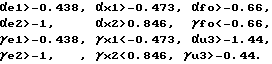
Выбираем коэффициенты закона управления (17), удовлетворяющие этим неравенствам: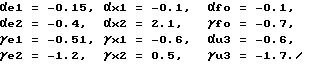
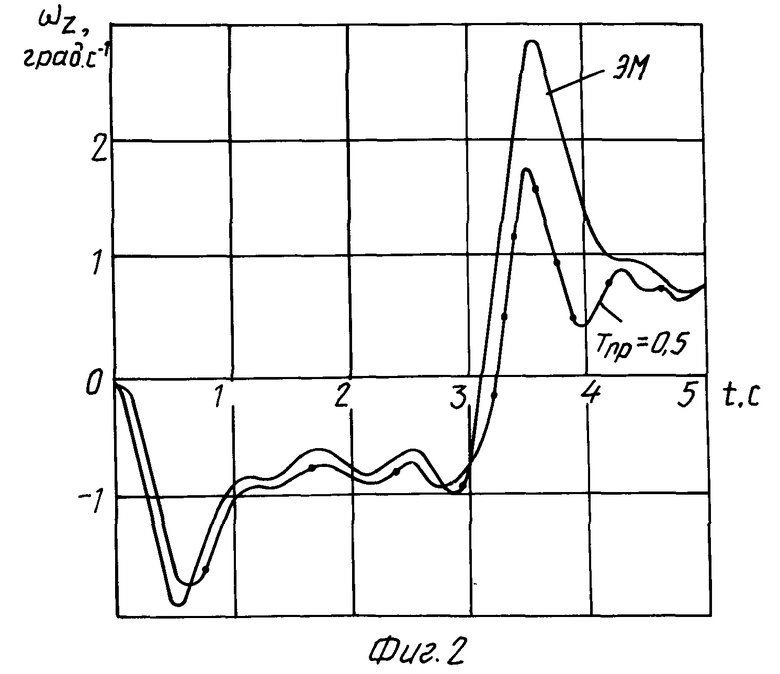
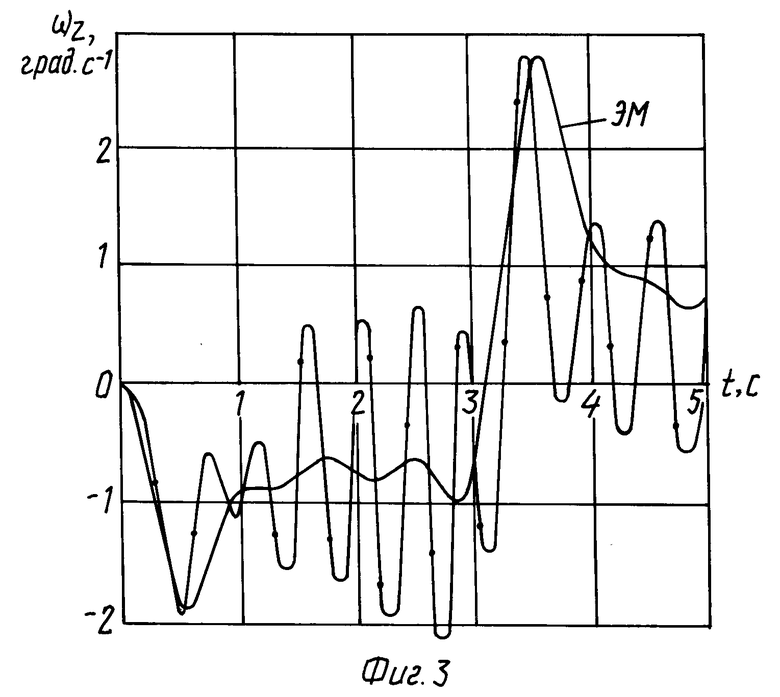
При включении синтезированной системы процессы ωz(t) и ωzм(t) для режима N 1 и режима N 2 практически не отличаются, что и было показано в прототипе. Однако при использовании в этой системе инерционных приводов возникают трудности с сохранением устойчивого скользящего режима. В качестве примера используем привод первого порядка с постоянной времени Tпр = 0.5с и привод второго порядка с параметрами: Tпр = 0.1c ξ = 1.5. Результаты моделирования синтезированной системы для режима N 1 представлены на фиг. 2 и фиг. 3. Из рисунков видно, что инерционность привода существенно влияет на процесс скольжения, особенно когда используется привод второго порядка, где помимо постоянной времени существенное влияние оказывает относительный коэффициент затухания.
При компенсации влияния инерционности привода попробуем учесть эту инерционность на этапе синтеза закона управления. Рассмотрим это на примере привода первого порядка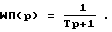
Передаточная функция ОУ (8) примет вид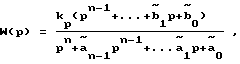
т. е. порядок числителя W(p) более чем на единицу меньше порядка знаменателя. В этом случае матрица B (11) в уравнениях неминимальной формы становится нулевой и основные (6) условия синтеза закона управления с переменной структурой не будут выполняться. Поэтому предлагается следующий подход при синтезе: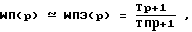
где T > Tп.
Постоянную времени T надо выбирать из условия совпадения реакций выходной управляемой координаты z(t) на типовые входные сигналы. В этом случае n-m=1 и указанные выше трудности должны быть преодолены. Размерность ЭМ увеличивается из таких же соображений, что и при изменении ПФ привода.
Проверку в численном эксперименте проведем для режима N 1.
Передаточную функцию ЭМ домножим на передаточную функцию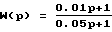 ,
,
при добавлении которой реакция ЭМ на входное воздействие существенно не изменилась. ПФ ЭМ в этом случае принимает вид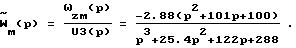
Неминимальная форма ЭМ в этом случае запишется следующим образом: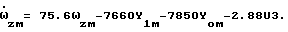

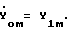
При синтезе ПФ привода примем в виде эквивалентной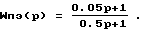
Тогда ПФ ОУ для режима 1 и НМФ ЭМ, ей соответствующая, принимают вид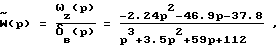

Неравенства, определяющие коэффициенты ЗУ, находятся так: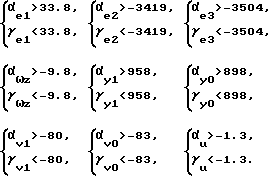
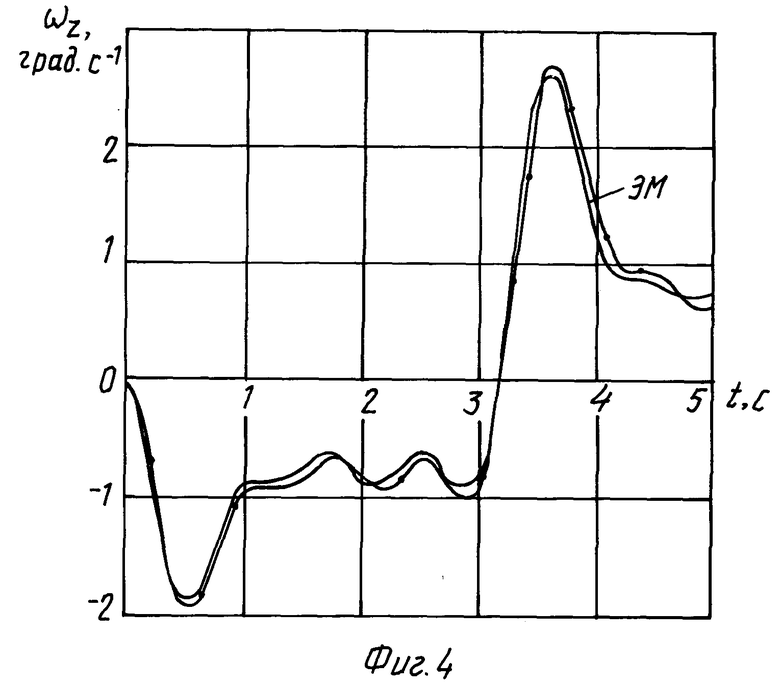
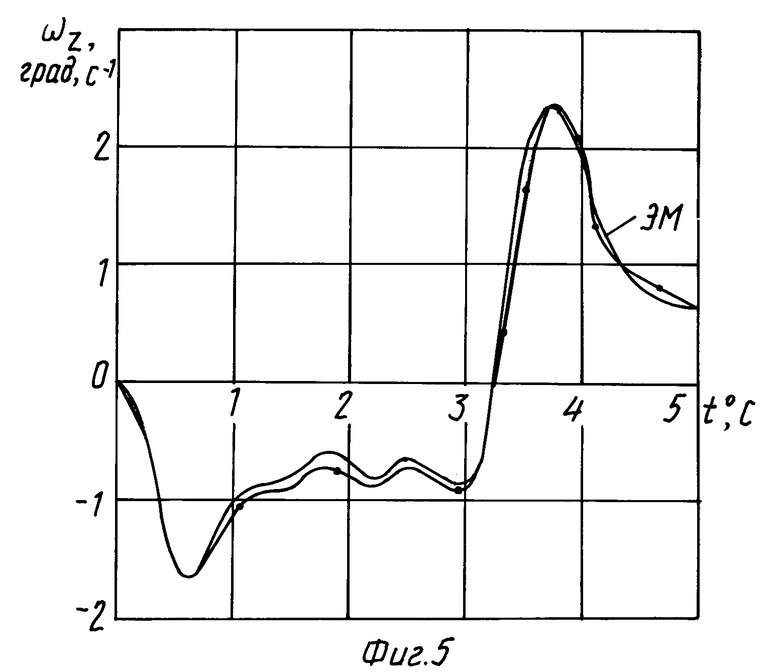
На фиг. 4, 5 представлены результаты моделирования синтезированной системы с компенсацией инерционности привода (КИП). Сравним с результатами фиг. 3, показывающими высокую эффективность предложенного метода компенсации.
Аналогичные исследования проведем для привода 2-го порядка. При синтезе параметры привода будем полагать такими, что были хуже реальных: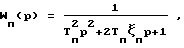
где Tп = 0.1с, ξп= 0.3.
Исследования показали, что эта передаточная функция может быть заменена эквивалентной: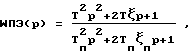
где Tп = 0.001, ξп = 1.5./
ПФ ЭМ, изменяя ее реакции на типовой входной сигнал, домножим на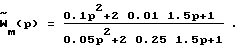
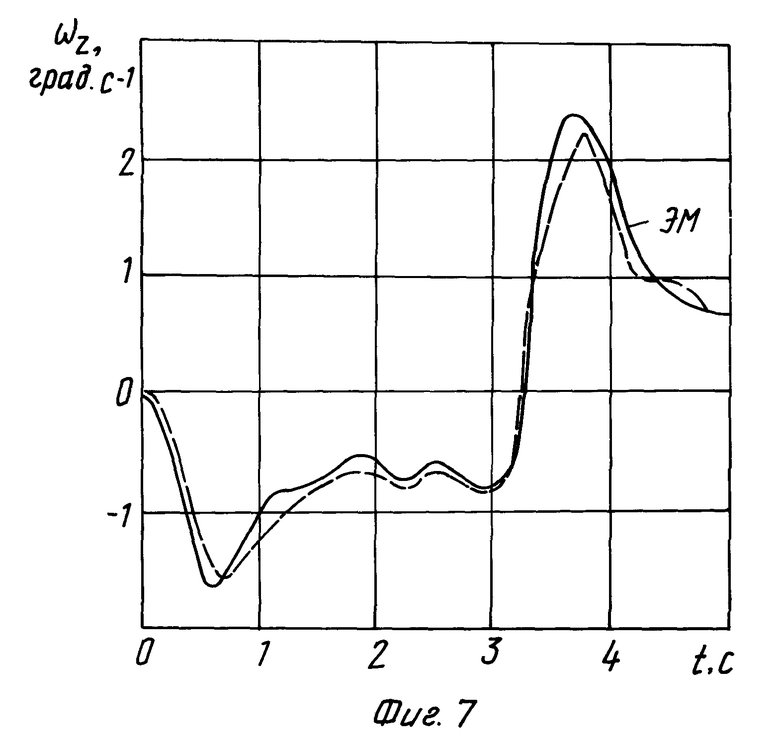
Результаты моделирования, полученные в результате синтеза, представленные на фиг. 5, свидетельствуют о высокой эффективности методики компенсации и для привода второго порядка. В заключении были проведены исследования синтезированной системы с переменной структурой при характеристиках привода, отличных от значений, принятых при синтезе:
вар. N 2 - Tn = 0.1 - ξn= 0.5,
вар. N 3 - Tn = 0.1 - ξn= 0.7,
вар. N 4 - Tn = 0.03 - ξn= 0.3,
вар. N 5 - Tn = 0.03 - ξn= 0.5.
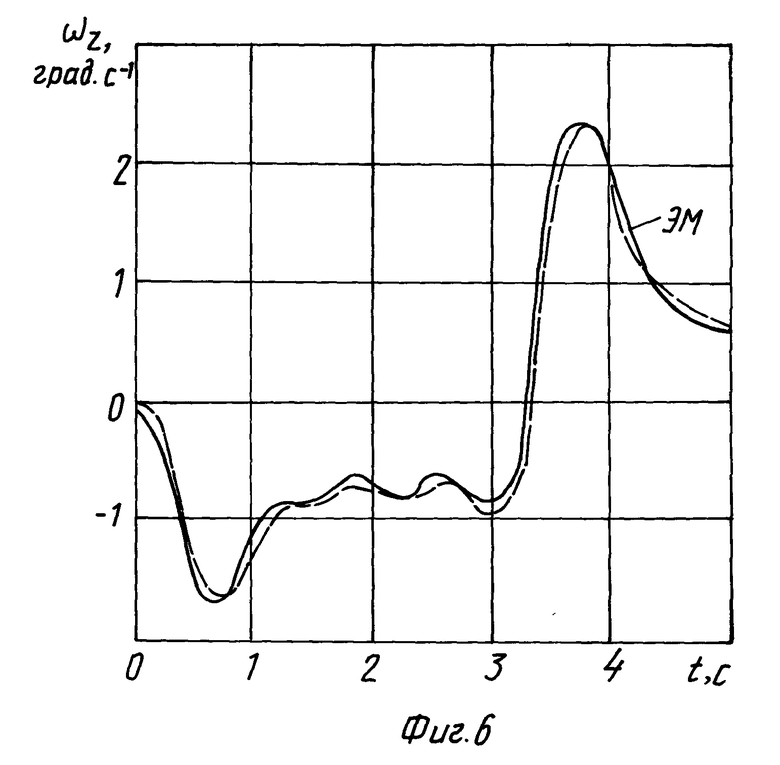
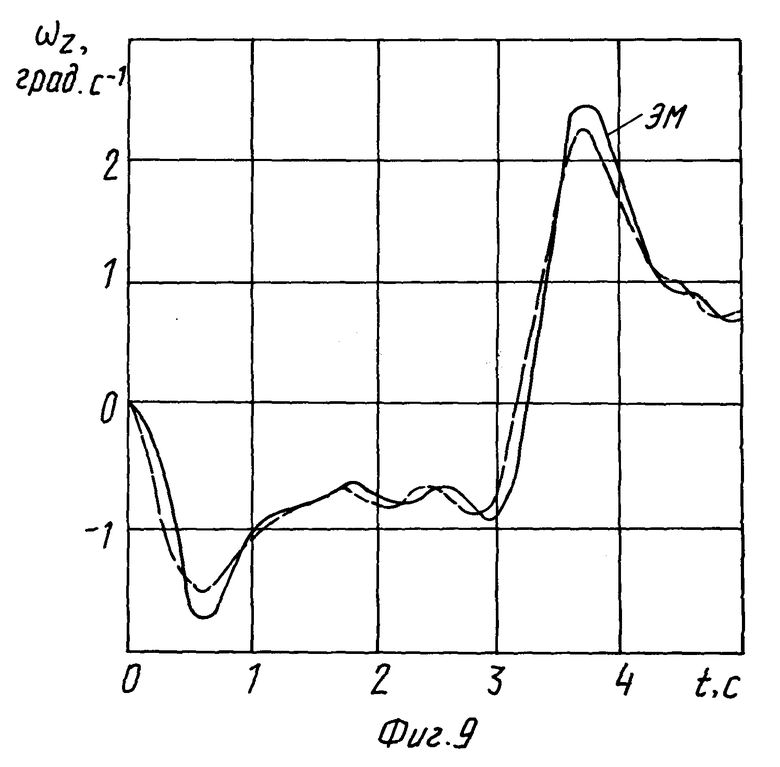
Результаты моделирования, приведенные на фиг. 6-9, доказывают возможность огрубления характеристик привода при синтезе. Однако, появление видимых отклонений реакции системы от реакции ЭМ наталкивает на мысль о необходимости уточнения пределов неравенств ЗУ СПС при рассмотрении различных вариантов приводов.
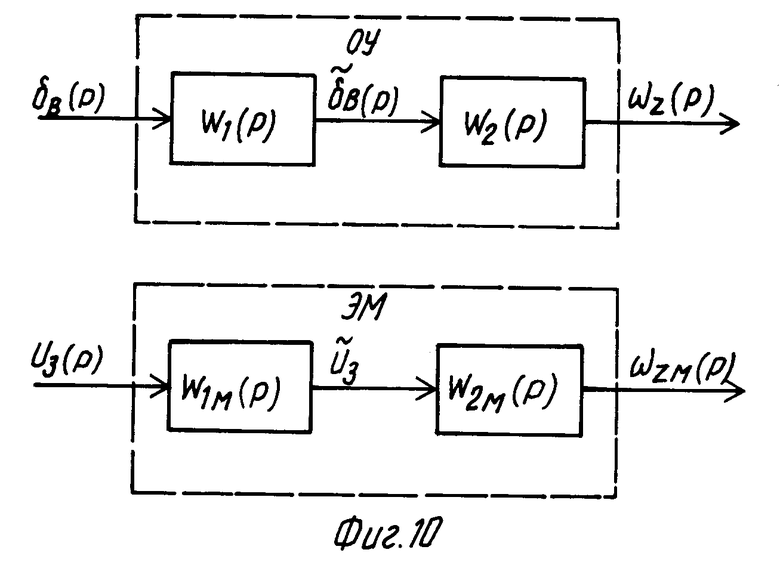
На фиг. 10 представлен ОУ и ЭМ в виде двух последовательно соединенных перердаточных функций,
где W1(p) • W2(p) =  (p), W1м(p) • W2м(p) =
(p), W1м(p) • W2м(p) =  (p).
(p).
В качестве технической реализации W1(p) и W1м(p) (блоки 2 и 21 на фиг. 1) могут быть предложены пассивные четырехполюсники, рассмотренные в [2].
Адаптивная система управления работает следующим образом. Задающее воздействие Uз с выхода задатчика 1 поступает на вход четырехполюсника 2, выход которого 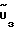 связан с выходом эталонной модели 3, выход которой
связан с выходом эталонной модели 3, выход которой 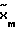 соединен с первым входом измерителя рассогласования 5. На второй вход измерителя рассогласования поступает сигнал
соединен с первым входом измерителя рассогласования 5. На второй вход измерителя рассогласования поступает сигнал 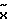 с выхода объекта управления 22. На выходе измерителя 5 формируется сигнал рассогласования
с выхода объекта управления 22. На выходе измерителя 5 формируется сигнал рассогласования 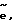 который поступает на первый вход блока 16, вход блока 8 и блока 6.
который поступает на первый вход блока 16, вход блока 8 и блока 6.
Усилитель 16 формирует сигнал управления 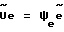 путем изменения коэффициента передачи канала управления по величине и знаку согласно следующему закону:
путем изменения коэффициента передачи канала управления по величине и знаку согласно следующему закону: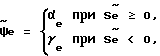
где 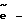 сигнал рассогласования измерителя 5,
сигнал рассогласования измерителя 5,
S - сигнал переключения,
αe и γe - переменные коэффициенты усилителя 16, формирующего сигнал управления.
Знаки сигнала рассогласования  и сигнала переключения S определяются с помощью блоков 7 и 8. Сравнение знаков (т.е. определения знака логического произведения
и сигнала переключения S определяются с помощью блоков 7 и 8. Сравнение знаков (т.е. определения знака логического произведения 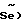 сигнала рассогласования
сигнала рассогласования  и сигнала переключения S осуществляется в множителе 12, выходной сигнал которого управляет работой блока 16.
и сигнала переключения S осуществляется в множителе 12, выходной сигнал которого управляет работой блока 16.
Задающее воздействие uз с выхода задатчика 1 поступает также на первый вход усилителя 17 и вход блока 9. Усилитель 17 формирует сигнал управления Uз = ηuзuз по следующему закону: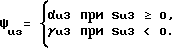
где uз - задающее воздействие задатчика 1,
S - сигнал переключения,
αu3 и γuз - переменные коэффициенты усилителя 17.
Знак uз определяется с помощью блока 9. Сравнение знаков задающего воздействия uз и сигнала переключения S осуществляется в множителе 13, выходной сигнал которого управляет работой усилителя 17.
Выходной сигнал 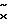 поступает также на первый вход усилителя 17 и вход блока 10. Усилитель 17 формирует сигнал управления
поступает также на первый вход усилителя 17 и вход блока 10. Усилитель 17 формирует сигнал управления 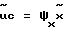 по следующему закону:
по следующему закону: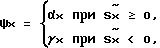
где 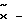 выходной сигнал объекта управления,
выходной сигнал объекта управления,
S - сигнал переключения,
αx и γx - переменные коэффициенты усилителя 17.
Знак выходного сигнала 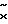 определяется с помощью блока 10. Сравнение знаков выходного сигнала
определяется с помощью блока 10. Сравнение знаков выходного сигнала 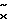 и сигнала S осуществляется в множителе 14, выходной сигнал которого управляет работой усилителя 17.
и сигнала S осуществляется в множителе 14, выходной сигнал которого управляет работой усилителя 17.
И, наконец, сигнал управления U с выхода сумматора 20, пройдя через формирующий фильтр 4, имеющий передаточную функцию для объекта второго порядка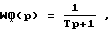
поступает на первый вход усилителя 19 и вход блока 11. Усилитель 19 формирует сигнал управления 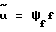 по следующему закону:
по следующему закону: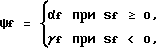
где f - выходной сигнал формирующего фильтра 4,
S - сигнал переключения,
αf и γf - переменные коэффициенты усилителя 19.
Знак выходного сигнала формирующего фильтра 4 определяется с помощью блока 11. Сравнение знаков выходного сигнала переключения S осуществляется в множителе 15, выходной сигнал которого управляет работой усилителя 19.
Литература
1. Авторское свидетельство СССР N 1659980 А1 от 30.06.91.
2. Макаров И. М. , Менский Б.М. Линейные автоматические системы. М., "Машиностроение", 1977, с. 441-452.
| название | год | авторы | номер документа |
|---|---|---|---|
| АДАПТИВНАЯ СИСТЕМА УПРАВЛЕНИЯ С ПЕРЕМЕННОЙ СТРУКТУРОЙ | 1998 |
|
RU2132079C1 |
| Адаптивная система управления с переменной структурой | 1988 |
|
SU1659980A1 |
| УСТРОЙСТВО ОБРАБОТКИ СИГНАЛОВ РАДИОЛОКАЦИОННОЙ СТАНЦИИ БОКОВОГО ОБЗОРА | 1998 |
|
RU2124738C1 |
| УСТРОЙСТВО ДЛЯ ОЦЕНКИ КАЧЕСТВА ПИЛОТИРОВАНИЯ САМОЛЕТА ЛЕТЧИКОМ | 1998 |
|
RU2136046C1 |
| ЭЛЕКТРИЧЕСКОЕ УСТРОЙСТВО ИЗМЕРЕНИЯ ПЛОТНОСТИ ЖИДКОСТИ В ГИДРОДИНАМИЧЕСКОЙ ТРУБЕ | 1998 |
|
RU2130176C1 |
| УСТРОЙСТВО ПОДАВЛЕНИЯ УЗКОПОЛОСНЫХ ПОМЕХ | 1998 |
|
RU2132592C1 |
| ИСТОЧНИК ЭЛЕКТРОПИТАНИЯ | 1998 |
|
RU2132107C1 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ЧАСТОТЫ ПУЛЬСА | 1994 |
|
RU2118119C1 |
| ЭЛЕКТРИЧЕСКОЕ УСТРОЙСТВО ИЗМЕРЕНИЯ ПЛОТНОСТИ ЖИДКОСТИ В ГИДРОДИНАМИЧЕСКОЙ ТРУБЕ ТЕРМОСОПРОТИВЛЕНИЯМИ | 1998 |
|
RU2133022C1 |
| УСТРОЙСТВО ДЛЯ ПОДАВЛЕНИЯ УЗКОПОЛОСНЫХ АКТИВНЫХ ПОМЕХ | 1996 |
|
RU2118047C1 |



Изобретение относится к области автоматики и может быть применено при управлении динамическими объектами с одним входом и одним выходом. Технический результат изобретения заключается в расширении области применения системы за счет возможности использования в ней инерционного привода. Система содержит задатчик входного сигнала, два блока четырехполюсников, эталонную модель, формирующий фильтр, измеритель рассогласования, блок формирования коэффициентов усиления, блоки релейных элементов, блоки умножителей, масштабирующие усилители с переменным коэффициентом, сумматор и объект управления. 10 ил., 2 табл.
Адаптивная система управления с переменной структурой, содержащая задатчик, выходом подключенный к третьему блоку релейных элементов и сигнальному входу второго масштабирующего усилителя с переменным коэффициентом, измеритель рассогласования, первым входом подключенный к выходу эталонной модели, вторым входом связанный с выходом объекта управления, входом четвертого блока релейных элементов и сигнальным входом третьего масштабирующего усилителя с переменным коэффициентом, а выходом - с входами блока формирования коэффициентов усиления, второго блока релейных элементов и сигнальным входом первого масштабирующего усилителя с переменным коэффициентом, первый блок релейных элементов, вход которого подключен к выходу формирования коэффициентов усиления, а выход - к первым входам первого, второго, третьего и четвертого блоков умножителей, вторые входы которых подключены соответственно к выходам второго, третьего, четвертого и пятого блоков релейных элементов, выходы первого, второго, третьего и четвертого блоков умножителей связаны соответственно с управляющими входами первого, второго, третьего и четвертого масштабирующих усилителей с переменным коэффициентом, выходы которых подключены соответственно к первому, второму, третьему и четвертому входам сумматора, выход сумматора связан с входом формирующего фильтра, выход которого соединен с входом пятого блока релейных элементов и сигнальным входом четвертого масштабирующего усилителя с переменным коэффициентом, отличающаяся тем, что дополнительно введены первый блок четырехполюсника, вход которого подключен к выходу задатчика входного сигнала, а выход - к входу эталонной модели, и второй блок четырехполюсника, вход которого связан с выходом сумматора, а выход - с входом объекта управления.
| Адаптивная система управления с переменной структурой | 1988 |
|
SU1659980A1 |
| Самонастраивающаяся система управления с эталонной моделью | 1990 |
|
SU1827664A1 |
| Макаров И.М., Менский Б.М | |||
| Линейные автоматические системы | |||
| - М.: Машиностроение, 1977, с.441-452 | |||
| Физический энциклопедический словарь | |||
| - М.: Сов | |||
| энциклопедия, 1966, т.5, с.414. | |||
Авторы
Даты
1999-05-20—Публикация
1998-03-30—Подача