Изобретение относится к строительству, а конкретно к способам создания строительных ферм.
Известные фермы, например ферма Шухова [1, стр. 106, рис. 4.16] является результатов изобретения автора, из этого подхода невозможно было отыскать какого-либо стройного способа-алгоритма, и все последующие фермы создавались, как правило, не в связи, а вопреки известному способу.
Известен [1, стр. 18, второй абзац сверху] способ создания строительных ферм путем последовательного присоединения к основному треугольнику узлов, а именно двух стержней, не лежащих на одной прямой, соединенных шарнирно. Любое соединение трех стержней в такой схеме может быть принято в качестве базового треугольника. Можно утверждать, что именно способ наращивания неизменяемого треугольника присоединения путем стержней с одним узлом, есть единственный отработанный способ, который и может быть принят в качестве прототипа.
Главными недостатками способа прототипа является невозможность создания сложных ферм и примитивизм получаемых конструкций.
Задачей настоящего изобретения является создание способа, который позволил бы создавать сложные фермы.
Решение поставленной задачи достигается тем, что по найденному значению числа стержней и узлов, определяется число звеньев кинематической цепи, представляющей собой группы Ассура, составляется универсальная структурная система с выбором наиболее сложного звена цепи и находятся все виды звеньев цепи. Затем строится кинематическая цепь при условии, когда она имеет два выхода и проводится связка кинематических пар в узлы. Замыкание выходов на опорах - заключительный этап построения ферм.
Сущность способа заключается в следующем.
На фиг.1 - схема кинематической цепи.
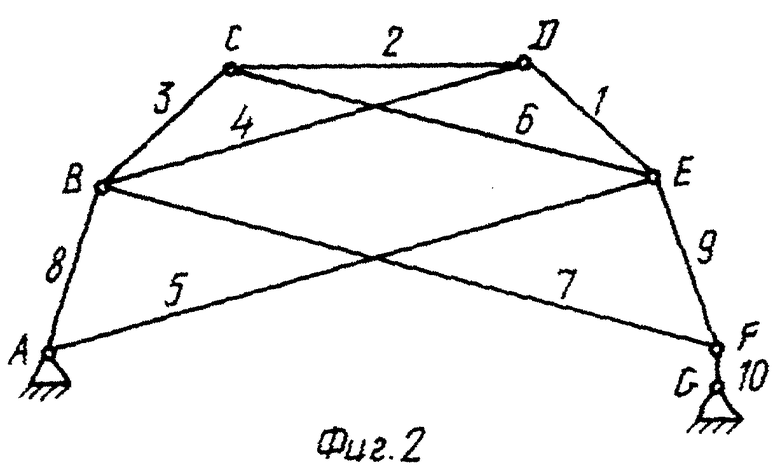
На фиг.2 - схема строительной фермы.
Введем понятие τ- угольника кинематической цепи. τ- Угольником будем называть звено, входящее в τ- кинематических пар с другими звеньями. Очевидно, что τ- угольник имеет τ геометрических элементов, если он свободен, или τ кинематических пар, если он находится в составе кинематической цепи. Любое звено в кинематической цепи, имеющее наибольшее число "углов", будет базисным звеном, которое определит конкретное τ. Приняв один из τ- угольников за τ- звено и зная все остальные звенья, можно сосчитать общее число кинематических пар, которое определяется как
p = τ+(τ-1)aτ-1+...+iai+...+2a2+a1, (1)
где ai - звенья, добавляющие по i пар в кинематическую цепь.
Общее число звеньев цепи тогда определится как
n = 1+aτ-1+...+ai+...+a2+a1, (2)
Известно [1] , что для статически определимой неизменяемой фермы между числом стержней n и числом узлов S существует связь
nф = 2S-3 (3)
Найдем связь между параметрами зависимости (3) и параметрами кинематических цепей. В соответствии с широко известным принципом Ассура Л.В. [2, стр. 52, 12] все механические подвижные системы создаются путем присоединения к ведущим звеньям таких групп звеньев, подвижность которых равняется нулю, т.е. группам Ассура. Подвижность плоских шарнирных механических систем определяется [2, стр. 40, формула (2.6)] известной формулой Чебышева П.Л.
W = 3n - 2p (4)
где W - подвижность или число степеней свободы системы,
n - число звеньев,
p - число шарниров в системе.
Группа Ассура удовлетворяет условию W = 0, т.е.
na = 2p/3 (5)
Здесь na обозначает число звеньев группы Ассура.
При подсчете стержней звено, соединяющее ферму со стойкой в подвижной опоре в формуле (2) не учитывается, поэтому всегда между na и nф существует связь
na = nф|1. (6)
Из (5) и (3) следует, что любая ферма может быть получена из групп Ассура при условии, что число узлов в ферме S определится как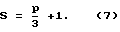
Для любой плоской кинематической цепи из зависимостей (1), (2) и (4) можно составить систему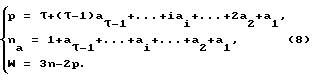
По этой системе можно найти все виды и количество звеньев кинематической цепи, необходимой для построения групп Ассура.
Обратимся к понятию числа ветвей кинематической цепи. Число ветвей или параметров γ цепи есть число свободных пар цепи. Число ветвей есть разница между числом кинематических пар p и числом реализованных пар. Так как в процессе построения цепи к τ- угольнику присоединяется (n-1) звеньев, то
γ = p-(n-1). (9)
Когда цепь сложная, т.е. в ней присутствуют изменяемые замкнутые контуры, число свободных выходов цепи δ и число образовавшихся замкнутых контуров в цепи α связываются зависимостью
γ = α+δ. (10)
Для того чтобы из кинематической цепи, представляющей собой группу Ассура, синтезировать ферму, необходимо произвести совмещение или связывание кинематических пар в узлы.
Пользуясь этой процедурой, можно из известной фермы путем перевязывания узлов получать иные формы ферм, в которых число стержней и число узлов будет одинаковым и соответствовать условию (3).
Рассмотрим предлагаемый метод создания плоской двухопорной фермы, состоящей из 9 стержней и 6 узлов. По зависимости (6) группа Ассура имеет 10 стержней, а по (5) число кинематических пар V класса в цепи - 15.
Для построения кинематической цепи такой группы необходимо определить виды и количество звеньев цепи ai, предварительно задавшись τ. Примем τ = 4. Решая систему (8) через a3 получаем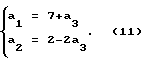
Решениями системы (11) будут
a3 = 1, a2 = 0, a1 = 8 и
a3 = 0, a2 = 2, a1 = 7.
Оба решения пригодны для синтеза групп. Воспользуемся первым решением, когда в цепи кроме базового четырехугольника ( τ- угольника) используется одно звено a3 и восемь звеньев a1. Для двухопорной фермы или для группы Ассура с двумя выходами (δ = 2) имеем по (10) α = 4, то есть группа должна быть построена с четырьмя замкнутыми изменяемыми контурами. Это значит, что четыре звена a1 будут применены не как линейные, а в более сложном исполнении.
Вариант группы Ассура приведен на фиг. 1. Все звенья и все пары специально обозначены.
Чтобы получить из этой группы нулевой подвижности ферму, произведем в соответствии с заявленным способом связывание узлов, то есть совмещение кинематических пар, что и показано на фиг. 2.
Отметим, что по найденным из системы (8) параметрам можно построить и другие группы Ассура, а следовательно, и другие фермы строительного назначения.
Литература
1. Дарков А.В. Шапошников Н.Н. Строительная механика. - М.: Высшая школа, 1986, 607 с.
2. Артоболевский И.К. Теория механизмов и машин. Издание 4-е. - М.: Наука, 1988.
| название | год | авторы | номер документа |
|---|---|---|---|
| САМОУСТАНАВЛИВАЮЩАЯСЯ ПЯТИКОНТАКТНАЯ ВРАЩАТЕЛЬНАЯ КИНЕМАТИЧЕСКАЯ ПАРА | 1998 |
|
RU2137965C1 |
| РЫЧАЖНЫЙ МЕХАНИЗМ ДЛЯ РАЗДЕЛЕНИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ | 2001 |
|
RU2207462C1 |
| КРИВОШИПНО-ПОЛЗУННЫЙ МЕХАНИЗМ ПРЕССА | 2001 |
|
RU2201348C1 |
| РЕДУКТОР ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ | 1999 |
|
RU2150626C1 |
| ЩЕКОВАЯ ДРОБИЛКА | 1998 |
|
RU2142850C1 |
| КРИВОШИПНО-ШАТУННЫЙ МЕХАНИЗМ | 2001 |
|
RU2210692C1 |
| РЫЧАЖНЫЙ МЕХАНИЗМ С ПОДВИЖНЫМ ПРИВОДОМ | 2002 |
|
RU2229641C2 |
| ПРОТЕЗ КИСТИ | 1998 |
|
RU2141289C1 |
| МАШИНА ДЛЯ УКЛАДКИ В ТАРУ ИЗДЕЛИЙ УДЛИНЕННОЙ ФОРМЫ | 2001 |
|
RU2176973C1 |
| БУРОВОЙ МАНИПУЛЯТОР | 2003 |
|
RU2242578C1 |
Изобретение относится к области строительства, а конкретно к способах создания строительных ферм. Технической задачей изобретения является создание способа сложных ферм различного назначения. Способ включает установление потребного числа стержней и узлов, удовлетворяющих условию ее статической определимости, при этом по найденному числу стержней определяют число звеньев кинематической цепи, представляющей собой структурную группу Ассура, производят выбор наиболее сложного звена цепи и находят все виды и числа звеньев цепи, а затем строят кинематическую цепь при условии, когда она имеет два выхода, и проводят процедуру связывания кинематических пар в узлы с замыканием выходов на опоры. 2 ил.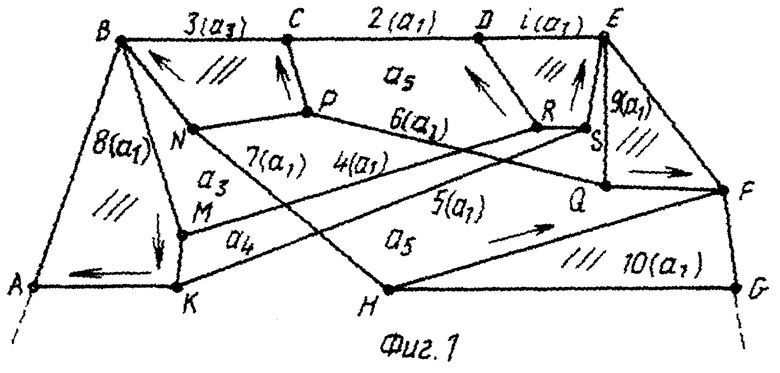
Способ создания конструктивных схем строительных ферм, включающий установление потребного числа стержней и узлов, удовлетворяющих условию ее статической определимости, отличающийся тем, что по найденному числу стержней определяют число звеньев кинематической цепи, представляющей собой структурную группу Ассура, производят выбор наиболее сложного звена цепи и находят все виды и числа звеньев цепи, а затем строят кинематическую цепь при условии, когда она имеет два выхода, и проводят процедуру связывания кинематических пар в узлы с замыканием выходов на опоры.
| АРТОБОЛЕВСКИЙ И.К | |||
| Теория механизмов и машин | |||
| - М.: Наука, 1988, с.52 и 12 | |||
| ДАРКОВ А.В | |||
| и др | |||
| Строительная механика | |||
| - М.: Высшая школа, 1986, с.607 | |||
| Способ извлечения иода | 1948 |
|
SU76355A1 |
| US 4982545 A, 08.01.1991. | |||
Авторы
Даты
2000-04-27—Публикация
1998-07-07—Подача