СПОСОБ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ ОСЕЙ КООРДИНАТ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ ОБЪЕКТА ОТНОСИТЕЛЬНО БАЗОВОЙ СИСТЕМЫ КООРДИНАТ (ЕГО ВАРИАНТЫ) Российский патент 2000 года по МПК B64G1/24 G01S5/02 G01S5/04 G01S5/00 

Изобретение относится к области навигации различных объектов, движущихся в инерциальном пространстве и имеющих на борту инерциальную навигационную систему.

К таким объектам могут относиться наземные и морские транспортные средства (автомобили, суда), а также воздушные и космические летательные аппараты (самолеты, ракеты, космические аппараты).

Известен способ определения положения трехосной навигационной системы по одновременным измерениям гравитационного ускорения и угловой скорости вращения Земли [1].

Способ используется, в основном, для начальной выставки инерциальных систем неподвижных относительно Земли объектов, причем в качестве базовой часто принимают географическую систему координат. Способ не может быть применен для движущихся объектов, испытывающих ускорения и угловые скорости.

Известен способ определения положения трехосной навигационной системы относительно базовой системы координат, заданной известными оптическими направлениями [2].

Способ используется как для начальной выставки осей навигационной системы неподвижных объектов по известным направлениям, например, на выбранные звезды, так и в процессе движения объекта.

Известен также способ астронавигации по патенту N 2033949 РФ (МКИ⁶ B 64 G, 1/24) включающий совмещение общей плоскости чувствительности датчиков Земли и Полярной звезды, содержащей продольную ось космического аппарата, с плоскостью "центр Земли-аппарат-Полярная звезда" (на основе измеренных угловых рассогласований по каналам тангажа, рысканья и крена), при этом определяется инерциальная долгота местоположения аппарата по азимуту угла поворота в поле зрения звездного датчика выбранной звезды вокруг направления "аппарат-Полярная звезда" относительно базы отсчета и с учетом инерциальной долготы этой базы, параметры которой запоминаются. При этом база отсчета - плоскость, содержащая направления "аппарат-Полярная звезда" и "аппарат-навигационная звезда", характеризуется инерциальной долготой, равной прямому восхождению Полярной звезды, и развернута относительно общей плоскости чувствительности датчиков Земли и Полярной звезды на угол, равный углу между плоскостью, содержащей направление "центр Земли-Полярная звезда" и "центр Земли-полюс Мира" и плоскостью, содержащей направление "центр Земли-Полярная звезда" и "центр Земли-навигационная звезда".

Однако эти способы требуют наличия на борту объекта оптических средств, например, астровизиров, и соблюдения условий видимости оптических ориентиров. Для наземных объектов и летательных аппаратов в атмосфере, подверженных влияниям метеоусловий, применение оптических средств ограничивает использование способа.

Наиболее близким аналогом предлагаемого способа определения положения осей координат инерциальной навигационной системы объекта относительно базовой системы координат является способ, основанный на одновременном измерении вектора ускорения в базовой и определяемой системах [3]. Причем вектор ускорения измеряется, по крайней мере, в двух точках траектории, где измеренные вектора ускорения не параллельны.

Способ может использоваться только в тех случаях, когда базовая система координат и система координат объекта испытывают одно и тоже ускорение, то есть носитель базовой системы и объект связаны механически и движутся по единой траектории. Например, самолет (объект) на палубе авианосца (носителя базовой системы), ракета (объект) на борту самолета-носителя (носителя базовой системы).

Способ имеет практический смысл в тех случаях, когда базовая система координат известна с лучшей точностью, чем система координат объекта, а также когда точность базовой системы координат достаточна для выполнения навигационной задачи объекта.

На практике часто эти условия не выполняются и способ не может быть применен, например, ракета носитель должна иметь точность ориентации осей инерциальной системы не хуже единиц угловых минут, в то время как самолет-носитель к моменту запуска ракеты-носителя может иметь ориентацию осей базовой системы координат с погрешностью - десятки угловых минут.

Задачей предлагаемого изобретения является повышение точности и надежности определения положения осей координат инерциальной навигационной системы движущегося объекта, обеспечение всепогодности этого определения.

Данная задача достигается тем, что в способе по варианту 1 определения положения осей координат инерциальной навигационной системы объекта относительно базовой системы координат, включающем навигационные измерения объекта, движущегося в инерциальном пространстве, в базовой системе координат и в инерциальной системе координат объекта
- в моменты времени t_i и t_i+1 измеряют координаты движущегося объекта в системе координат Глобальной навигационной системы типа "Глонас" или/и "Navstar", выбранной в качестве базовой системы координат;
- на участке траектории объекта t_i - t_i+1 измеряют вектор ускорения в инерциальной системе координат объекта, по которому определяют координаты объекта в те же моменты времени t_i и t_i+1;
- в моменты времени t_j и t_j+1 на участке траектории объекта, не параллельном участку предыдущих навигационных измерений, проводят аналогичные измерения координат объекта в базовой системе координат и в инерциальной системе координат объекта;
- затем по полученным координатам на каждом участке траектории t_i - t_i+1 и t_j - t_j+1, которых выбирают, по крайней мере, два, определяют вектора перемещения объекта L_i, L_j в базовой системе координат L_i ^B, L_j ^B и в инерциальной системе координат объекта L_i ^U, L_j ^U;
после чего определяют матрицу перехода между базовой системой координат и инерциальной системой координат объекта из системы уравнений
L_i ^B=AL_i ^U,
L_j ^B=AL_j ^U,
i,j = 1...n, i ≠ j,
где A - матрица перехода из базовой системы координат в инерциальную систему координат объекта,
n - количество участков траектории;
- при этом по компонентам матрицы A определяют положения осей координат инерциальной навигационной системы объекта относительно базовой.

В предлагаемом способе по варианту 2 определения положения осей координат инерциальной навигационной системы объекта относительно базовой системы координат, включающем навигационные измерения объекта, движущегося в инерциальном пространстве, в базовой системе координат и в инерциальной системе координат объекта
- в моменты временит t_i и t_i+1 измеряют вектор скорости движущегося объекта в системе координат Глобальной навигационной системы типа "Глонас" или/и "Navstar", выбранной в качестве базовой системы координат;
- на участке траектории объекта t_i - t_i+1 измеряют вектор ускорения в инерциальной системе координат объекта, по которому определяют вектор скорости объекта в те же моменты времени t_i и t_j+1;
- в моменты времени t_j и t_j+1 на участке траектории объекта, не параллельном участку предыдущих навигационных измерений, проводят аналогичные измерения вектора скорости объекта в базовой системе координат и в инерциальной системе координат объекта;
- затем по полученным векторам скоростей на каждом участке траектории t_i-t_i+1 и t_j-t_j+1, которых выбирают, по крайней мере, два, определяют приращения вектора скорости объекта ΔV_i, ΔV_j в базовой системе координат ΔV_i ^B,
ΔV_j ^B и в инерциальной системе координат объекта ΔV_i ^U, ΔV_j ^U;
- после чего определяют матрицу перехода между базовой системой координат и инерциальной системой координат объекта из системы уравнений
ΔV_i ^B = AΔV_i ^U,
ΔV_j ^B = AΔV_j ^U,
i, j = 1...n, i ≠ j,
где A - матрица перехода из базовой системы координат в инерциальную систему координат объекта,
n - количество участков траектории;
- при этом по компонентам матрицы A определяют положение осей координат инерциальной навигационной системы объекта относительно базовой.

В предлагаемом способе по варианту 3 определения положения осей координат инерциальной навигационной системы объекта относительно базовой системы координат, включающем навигационные измерения объекта, движущегося в инерциальном пространстве, в базовой системе координат и в инерциальной системе координат объекта
- в моменты времени t_i и t_i+1 измеряют координаты и вектор скорости движущегося объекта в системе координат Глобальной навигационной системы типа "Глонас" или/и "Navstar", выбранной в качестве базовой системы координат;
- на участке траектории объекта t_i-t_i+1 измеряют вектор ускорения в инерциальной системе координат объекта, по которому определяют координаты и вектор скорости объекта в те же моменты времени t_i и t_i+1;
- в моменты времени t_j и t_j+1 на участке траектории объекта, не параллельном участку предыдущих навигационных измерений, проводят аналогичные измерения координат и вектора скорости объекта в базовой системе координат и в инерциальной системе координат объекта;
- затем по полученным координатам и векторам скоростей на каждом участке траектории t_i-t_i+1 и t_j-t_j+1, которых выбирают, по крайней мере, два, определяют вектора перемещения объекта L_i, L_j и приращения вектора его скорости ΔV_i, ΔV_j в базовой системе координат L_i ^B, L_j ^B, ΔV_i ^B, ΔV_j ^B и в инерциальной системе координат объекта L_i ^U, L_j ^U, ΔV_i ^U, ΔV_j ^U;
- после чего определяют матрицу перехода между базовой системой координат и инерциальной системой координат объекта из системы уравнений
L_i ^B = AL_i ^B, ΔV_i ^B = AΔV_i ^U,
L_j ^B = AL_j ^U, ΔV_j ^B = AΔV_j ^U,
i, j = 1...n, i ≠ j,
где A - матрица перехода из базовой системы координат в инерциальную систему координат объекта,
n - количество участков траектории;
- при этом по компонентам матрицы A определяют положение осей координат инерциальной навигационной системы объекта относительно базовой.

В предлагаемом способе при движении объекта в инерциальном пространстве по прямолинейной траектории осуществляют его маневр, реализующий, по крайней мере, два непараллельных участка траектории, на которых проводят упомянутые навигационные измерения.

Существо предлагаемого способа иллюстрируется на чертежах, где:
1 - объект;
2 - оси координат инерциальной навигационной системы объекта X^U, Y^U, Z^U;
3 - оси координат базовой системы X^B, Y^B, Z^B;
4 - глобальная навигационная система типа "Глонас" ("Navstar");
t_i, t_i+1, t_j, t_j+1 - моменты времени, в которые определяют координаты движущегося объекта в базовой системе координат типа "Глонас" или/и "Navstar" и в инерциальной системе координат объекта;
L₁, L_j - вектора перемещения объекта соответственно на участке траектории t_i - t_i+1 и t_j-t_j+1,
ΔV_i, ΔV_j - приращение вектора скоростей объекта соответственно на участке траектории t_i-t_i+1 и t_j-t_j+1;
α,β,γ- углы, определяющие положение осей координат инерциальной навигационной системы объекта X^U, Y^U, Z^U относительно осей координат базовой системы X^B, Y^B, Z^B (углы Эйлера).

Способ отличается от известных аналогов тем, что в варианте 1
- в моменты времени t₁ и t_i+1 измеряют координаты движущегося объекта 1 в системе координат 3 Глобальной навигационной системы 4, выбранной в качестве базовой системы координат [4];
- в те же моменты времени t_i и t_i+1 определяют те же координаты объекта 1 в инерциальной навигационной системе координат объекта 2 по измерениям вектора ускорения на участке траектории t_i-t_i+1;
- в моменты времени t_j и t_j+1 на участке траектории объекта 1, не параллельном участку предыдущих навигационных измерений, производят аналогичные измерения координат объекта в базовой системе координат 3 и в инерциальной системе координат объекта 2;
- затем по полученным координатам объекта 1 на каждом участке траектории t_i-t_i+1 и t_j-t_j+1, которых выбирают, по крайней мере, два, определяют вектора перемещения L_i, L_j в базовой системе координат 3 L_i ^B, L_j ^B, и в инерциальной системе координат объекта 2L_i ^U, L_j ^U.

- после чего определяют углы рассогласования между базовой системой координат 3 и инерциальной системой координат объекта 2 из системы уравнений
L_i ^B=AL_i ^U,
L_j ^B=AL_j ^U,
i,j=1...n, i,j ≠j
где A - матрица перехода из базовой системы координат 3 в инерциальную систему координат объекта 2,
n - количество участков траекторий;
- по полученным компонентам матрицы перехода А определяют положение осей координат инерциальной навигационной системы объекта 2 относительно базовой 3; то есть определяют углы рассогласования между ними α,β,γ (углы Эйлера).

Способ отличается также тем, что в варианте 2
- в моменты времени t_i и t_i+1 измеряют вектор скорости движущегося объекта 1 в системе координат 3 Глобальной навигационной системы 4 типа "Глонас" (или/и "Navstar"), выбранной в качестве базовой системы координат;
- на участке траектории объекта 1 t_i-t_i+1 измеряют вектор ускорения в инерциальной системе координат объекта 2, по которому определяют вектор скорости объекта в те же моменты времени t_i и t_i+1;
- в моменты времени t_j и t_j+1 на участке траектории объекта, не параллельном участку предыдущих навигационных измерений, проводят аналогичные измерения вектора скорости объекта в базовой системе координат 3 и в инерциальной системе координат объекта 2;
- затем по полученным векторам скоростей на каждом участке траектории t_i-t_i+1 и t_j-t_j+1, которых выбирают, по крайней мере, два, определяют приращения вектора скорости объекта ΔV_i, ΔV_j в базовой системе координат 3 ΔV_i ^B, ΔV_j ^B и в инерциальной системе, координат 2 объекта ΔV_i ^U, ΔV_j ^U; - после чего определяют матрицу перехода между базовой системой координат 3 и инерциальной системой координат 2 объекта из системы уравнений:
ΔV_i ^B = AΔV_i ^U,
ΔV_j ^B = AΔV_j ^U,
i,j=1...n, i ≠j,
где A - матрица перехода из базовой системы координат в инерциальную систему координат объекта,
n - количество участков траектории;
- при этом по компонентам матрицы A определяют положение осей координат инерциальной навигационной системы 2 объекта относительно базовой 3.

Предлагаемый способ по варианту 3 отличается тем, что:
- в моменты времени t_i и t_i+1 измеряют координаты и вектор скорости движущегося объекта 1 в системе координат Глобальной навигационной системы 4 "Глонас" или/и "Navstar", выбранной в качестве базовой системы координат;
- на участке траектории объекта t_i-t_i+1 измеряют вектор ускорения в инерциальной системе координат 2 объекта, по которому определяют координаты и вектор скорости объекта 1 в те же моменты времени t_i и t_i+1;
- в моменты времени t_j и t_j+1 на участке траектории объекта 1, не параллельном участку предыдущих навигационных измерений, проводят аналогичные определения координат и вектора скорости объекта в базовой системе координат 3 и в инерциальной системе координат объекта 2;
- затем по полученным координатам и векторам скоростей на каждом участке траектории t_i-t_i+1 и t_j+t_j+1, которых выбирают, по крайней мере, два, определяют вектора перемещения объекта L_i, L_j и приращения вектора его скорости ΔV_i, ΔV_j в базовой системе координат 3 L_i ^B, L_j ^B, ΔV_i ^B, ΔV_j ^B и в инерциальной системе координат 2 объекта 1 L_i ^U, L_j ^U, ΔV_i ^U, ΔV_j ^U;
- после чего определяют матрицу перехода между базовой системой координат 3 и инерциальной системой координат 2 объекта 1 из системы уравнений
L_i ^B = AL_i ^U, ΔV_i ^B = AΔV_i ^U,
L_j ^B = AL_j ^U, ΔV_j ^B = AΔV_j ^U
i,j = 1...n, i≠j,
где A - матрица перехода из базовой системы координат в инерциальную систему координат объекта,
n - количество участков траектории;
- при этом по компонентам матрицы A определяют положение осей координат инерциальной навигационной системы 2 объекта относительно базовой 3.

Способ также отличается тем, что при движении объекта 1 в инерциальном пространстве по прямолинейной траектории, осуществляют его маневр, реализующий, по крайней мере, два непараллельных участка траектории, на которых проводят навигационные измерения.

Предлагаемый способ определения положения осей координат навигационной системы движущегося объекта позволяет определять с высокой точностью (единицы метров) большие перемещения объектов (тысячи километров) в любых погодных условиях с помощью Глобальных навигационных систем типа "Глонас" или/и "Navstar", работающих в радиодиапазоне.

Например, для таких движущихся объектов как самолеты, ракеты, космические аппараты, перемещения которых значительны, точность определения положения осей координат их навигационных систем может составлять единицы угловых секунд.

Отсутствие влияния погодных условий на навигационные измерения с помощью систем "Глонас" или "Navstar", в отличие от астронавигационных систем, обеспечивает способу высокую надежность и всепогодность. Примером реализации предлагаемого способа определения положения осей координат инерциальной навигационной системы объекта может служить авиационно-космическая система, использующая серийные самолеты-носители и запускаемые с их борта ракеты-носители. Самолеты-носители, как правило, имеют навигационные системы с точностью ориентации осей, достигающей десятки угловых минут, что является недостаточным для стартующей с его борта ракеты-носителя, точность ориентации осей навигационной системы которой должна быть не хуже единиц угловых минут, что достигается предложенным способом.

Литература
1. Г. А. Хлебников "Начальная выставка инерциальных навигационных систем", Военная академия имени Ф.Э. Дзержинского, М., 1994 г., стр. 225-228.

2. То же, стр. 230-231.

3. То же, стр. 237.

4. "Радиотехнические системы" под ред. Ю.М. Казаринова, М.: Высшая школа, 1990 г., стр. 304-306.

Изобретение относится к области навигации различных объектов, имеющих на борту инерциальную навигационного систему (самолетов, космических аппаратов, автомобилей, судов). Предлагаемый способ включает навигационные измерения в базовой и инерциальной системах координат объекта. В качестве базовой выбирают ту, которая используется в глобальной навигационной системе типа "Глонас" и "Navstar". В различные пары моментов времени на последовательных и непараллельных участках траектории измеряют координаты и/или векторы скорости объекта в обеих системах координат. При этом данные параметры движения определяют, измеряя вектор ускорения на этих участках. По координатам и/или скоростям на участках траектории определяют перемещения объекта и/или приращения его скорости. По ним строят матрицу перехода между базовой и инерциальной системами координат. По компонентам матрицы находят относительное положение осей координат обеих систем. Непараллельные участки траектории могут быть получены специальным маневром объекта. Изобретение позволяет повысить точность и обеспечивает всепогодность его реализации. 3 с. и 1 з.п. ф-лы, 1 ил.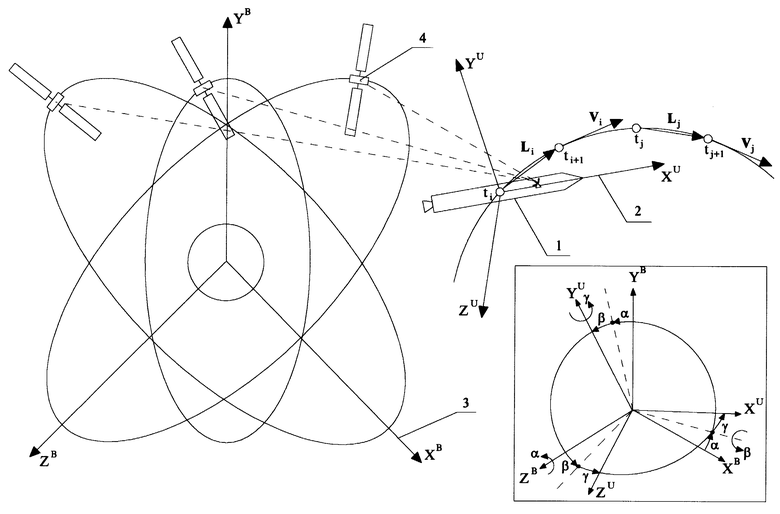

1. Способ определения положения осей координат инерциальной навигационной системы объекта относительно базовой системы координат, включающий навигационные измерения объекта, движущегося в инерциальном пространстве, в базовой системе координат и в инерциальной системе координат объекта, отличающийся тем, что в моменты времени t_i и t_i+1 измеряют координаты движущегося объекта в системе координат глобальной навигационной системы типа "Глонас" или/и "Navstar", выбранной в качестве базовой системы координат; на участке траектории объекта в период времени t_i - t_i+1 измеряют вектор ускорения в инерциальной системе координат объекта, по которому определяют координаты объекта в те же моменты времени t_i и t_i+1; в моменты времени t_j и t_j+1 на участке траектории объекта, не параллельном участку предыдущих навигационных измерений, проводят аналогичные определения координат объекта в базовой системе координат и в инерциальной системе координат объекта; затем по полученным координатам на каждом из, по меньшей мере, двух участков траектории в периоды времени t_i - t_i+1 и t_j - t_j+1 определяют векторы перемещения объекта в базовой (L_i ^B, L_j ^B) и в инерциальной (L_i ^U, L_j ^U) системах координат объекта, после чего определяют матрицу (A) перехода между базовой системой координат и инерциальной системой координат объекта из системы уравнений
L_i ^B = AL_i ^U,
L_j ^B = AL_j ^U,
i, j = 1 ... n, i ≠ j,
где n - количество участков траектории, при этом по компонентам матрицы A определяют положение осей координат инерциальной навигационной системы объекта относительно базовой. 2. Способ определения положения осей координат инерциальной навигационной системы объекта относительно базовой системы координат, включающий навигационные измерения объекта, движущегося в инерциальном пространстве, в базовой системе координат и в инерциальной системе координат объекта, отличающийся тем, что в моменты времени t_i и t_i+1 измеряют вектор скорости движущегося объекта в системе координат глобальной навигационной системы типа "Глонас" или/и "Navstar", выбранной в качестве базовой системы координат; на участке траектории объекта в период времени t_i - t_i+1 измеряют вектор ускорения в инерциальной системе координат объекта, по которому определяют вектор скорости объекта в те же моменты времени t_i и t_i+1; в моменты времени t_j и t_j+1 на участке траектории объекта, не параллельном участку предыдущих навигационных измерений, проводят аналогичные определения вектора скоростей объекта в базовой системе координат и в инерциальной системе координат объекта; затем по полученным векторам скоростей на каждом из, по меньшей мере, двух участков траектории в периоды времени t_i - t_i+1 и t_j - t_j+1 определяют приращения вектора скорости объекта в базовой (ΔV_i ^B, ΔV_j ^B) и в инерциальной (ΔV_i ^U, ΔV_j ^U) системах координат объекта, после чего определяют матрицу перехода (A) между базовой системой координат и инерциальной системой координат объекта из системы уравнений
ΔV_i ^B = AΔV_i ^U,
ΔV_j ^B = AΔV_j ^U,
i, j = 1 ... n, i ≠ j,
где n - количество участков траектории,
при этом по компонентам матрицы A определяют положение осей координат инерциальной навигационной системы объекта относительно базовой. 3. Способ определения положения осей координат инерциальной навигационной системы объекта относительно базовой системы координат, включающий навигационные измерения объекта, движущегося в инерциальном пространстве, в базовой системе координат и в инерциальной системе координат объекта, отличающийся тем, что в моменты времени t_i и t_i+1 измеряют координаты и вектор скорости движущегося объекта в системе координат глобальной навигационной системы типа "Глонас" или/и "Navstar", выбранной в качестве базовой системы координат; на участке траектории объекта в период времени t_i - t_i+1 измеряют вектор ускорения в инерциальной системе координат объекта, по которому определяют координаты и вектор скорости объекта в те же моменты времени t_i и t_i+1; в моменты времени t_j и t_j+1 на участке траектории объекта, не параллельном участку предыдущих навигационных измерений, проводят аналогичные определения координат и вектора скорости объекта в базовой системе координат и в инерциальной системе координат объекта; затем по полученным координатам и векторам скоростей на каждом из, по меньшей мере, двух участков траектории в периоды времени t_i - t_i+1 и t_j - t_j+1 определяют векторы перемещения и приращения скорости объекта в базовой (соответственно, L_i ^B, L_j ^B и ΔV_i ^B, ΔV_j ^B) и в инерциальной (соответственно, L_i ^U, L_j ^U и ΔV_i ^U, ΔV_j ^U) системах координат объекта, после чего определяют матрицу перехода (A) между базовой системой координат и инерциальной системой координат объекта из системы уравнений
L_i ^B = AL_i ^U, ΔV_i ^B = AΔV_i ^U,
L_j ^B = AL_j ^U, ΔV_j ^B = AΔV_j ^U,
i, j = 1 ... n, i ≠ j,
где n - количество участков траектории,
при этом по компонентам матрицы A определяют положение осей координат инерциальной навигационной системы объекта относительно базовой. 4. Способ по любому из пп.1 - 3, отличающийся тем, что при движении объекта в инерциальном пространстве по прямолинейной траектории, осуществляют его маневр, реализующий, по крайней мере, два непараллельных участка траектории, на которых проводят навигационные измерения.