Изобретение относится к измерительной технике и может быть использовано для определения физико-механических параметров жидких, твердых и газообразных сред, решения задач медицинской и технической диагностики.
Известен способ измерения нелинейного акустического параметра (НАП) (Железный В.Б., Ивлиев С.В. Способ измерения параметра нелинейности среды. - А. с. N 1233032, МКИ G 01 N 29/00 - опубл. БИ N 19, 1986), в котором устанавливают первый и второй высокочастотные преобразователи на расстоянии друг от друга, равном менее двух длин волн, излучаемых низкочастотным преобразователем, установленным под углом к направлению излучения высокочастотного сигнала. Излучают высокочастотный сигнал первым преобразователем и измеряют максимальный фазовый сдвиг между сигналами, излученным первым и принятым соответственно вторым преобразователями. Излучают высокочастотный сигнал вторым преобразователем и измеряют максимальный фазовый сдвиг между сигналами, излученным вторым и принятым первым преобразователями. По измеренным значениям максимальных фазовых сдвигов с учетом угла между направлениями распространения излученных низкочастотной и высокочастотной волн и расстояния между высокочастотными преобразователями определяют искомый параметр по формуле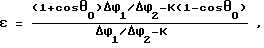
где ε - нелинейный акустический параметр среды; θ0 - угол между направлениями распространения низкочастотной и высокочастотной волн в случае, когда излучателем является первый, а приемником - второй высокочастотные преобразователи; ΔΦ1 и ΔΦ2 - измеренные максимальные фазовые сдвиги в высокочастотной волне, когда, соответственно, излучателем высокочастотной волны является первый преобразователь, а приемником - второй, и наоборот - излучателем является второй, а приемником - первый преобразователь;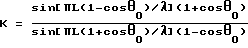
L - длина пути высокочастотной волны в поле низкочастотной; λ - длина низкочастотной волны.
Общим признаком аналога с заявляемым техническим решением является излучение в контролируемую среду двух акустических волн - низкочастотной и высокочастотной.
Недостатком этого способа являются низкая точность и достоверность определения НАП, обусловленная малостью измеряемых индексов фазовой модуляции. Известно (см. Зверев В.А., Калачев А.И. Модуляция звука звуком при пересечении акустических волн. // Акустический журнал. 1970, т. 16, вып. 2. С. 245-252), что величина фазовой модуляции в аналоге
ΔΦ ≈ εM = εν0/c0,
где M - акустическое число Маха; ν0- амплитуда колебательной скорости в низкочастотной волне; c0 - скорость звука; ε - НАП. В акустике, как правило, M ≈ 10-5 - 10-4 (см.: Ультразвук. Маленькая энциклопедия. Глав. ред. Голямина И. П. . - М.: Советская энциклопедия, 1979. С. 209). Поэтому величина ΔΦ лежит в пределах 3,5-10-5 - 3,5-10-4. Такие значения ΔΦ сравнимы по порядку величины с фазовыми шумами электронных трактов, возможными флуктуациями фазы за счет малых механических колебаний измерительных преобразователей друг относительно друга и т.д. Это приводит к значительному снижению точности измерения НАП.
В качестве прототипа выбран способ определения НАП твердых тел (Саперов В. А. , Зиновьева Г.П. Способ измерения нелинейного акустического параметра твердых тел и устройство для его осуществления. - А.с. N 1236363, МКИ G 01 N 29/00 - Опубл. БИ N 21, 1986), в котором в среду излучают акустическую волну, состоящую из двух гармоник - первой (с частотой ω) и второй (с частотой 2ω), принимают и регистрируют волну второй гармоники. Эти признаки являются общими для прототипа и заявляемого способа. Амплитуда принимаемой волны с частотой 2ω зависит от фазового инварианта ψ = Φ2-2Φ1 в излучаемой волне: при изменении фазового инварианта от 0 до π амплитуда принимаемой второй гармоники изменяется от максимального своего значения Umax до минимального Umin. Изменяя фазовый инвариант в излучаемой волне от 0 до π, измеряют максимальное и минимальное значения амплитуды принятой второй гармоники и вычисляют параметр, называемый в рассматриваемом изобретении коэффициентом модуляции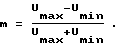
Измерив электрические мощности, потребляемые излучателем на первой и второй гармониках сигнала, определяют НАП с учетом рассчитанного коэффициента модуляции по формуле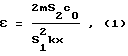
где k =ω/c0 волновое число; c0 - скорость звука в среде; x - расстояние между излучателем и приемником; S1 и S2 - амплитуды колебательного смещения в первой и второй гармониках излучаемого сигнала, рассчитываемые по формулам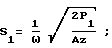
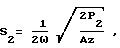
где P1 и P2 - электрические мощности, потребляемые излучателем на первой и второй гармониках, которые в данном способе приравниваются соответствующим акустическим мощностям; A - площадь поверхности излучателя ультразвука; z - волновое сопротивление среды.
Недостатками приведенного способа являются:
1) - низкая достоверность измерения НАП, следующая из немонотонного характера пространственного распределения амплитуды второй гармоники S2(x) в случае Φ2-2Φ1= π (Гаврилов А.М., Савицкий О.А. К вопросу об использовании эффекта вырожденного параметрического усиления. // Акуст. журн. 1992. Т. 38, N 4, с. 675). Наличие этой особенности у S2(x) не учитывается в данной работе;
2) - низкая достоверность определения НАП по выражению (1) в связи с ошибкой, допущенной при ее выводе. В этом легко убедиться, оценив размерность ε, которая согласно (1) равна (1/c), хотя НАП по определению безразмерен. С целью устранения ошибки обратимся к выражению для амплитуды колебательной скорости второй гармоники, генерируемой в среде синусоидальным сигналом конечной амплитуды (Шутилов В.А. Основы физики ультразвука. - Л.: Изд. ЛГУ, с. 82)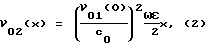
где ν01(0) - амплитуда колебательной скорости 1-й гармоники в излучаемой волне при x = 0; ν02(x) - пространственное распределение амплитуды колебательной скорости 2-й гармоники. Перейдя в (2) к колебательному смещению, получим выражение для НАП в виде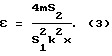
3) - низкая точность определения НАП, связанная с приближенным характером используемой физической модели нелинейных процессов в бигармонической волне, т.к. не учитываются изменения амплитуд 1-й и 2-й гармоник в процессе распространения за счет оттока энергии в другие компоненты спектра, генерируемые за счет взаимодействия и самовоздействия;
4) - низкая точность определения НАП, обусловленная допущением, что электроакустический коэффициент полезного действия (КПД) излучателя на частотах 1-й и 2-й гармоник равен единице. Однако даже при работе на механическом резонансе электроакустический КПД у существующих электроакустических преобразователей не превышает 70-80%. Реально эта величина может существенно отличаться в меньшую сторону. Неучет фактического КПД вносит систематическую погрешность в определение амплитуд смещения (S1, S2), а через них - погрешность в величину НАП.
Перед изобретателями стояла задача: 1) разработать способ достоверного определения НАП; 2) повысить точность измерения НАП.
Техническим результатом предлагаемого изобретения является повышение достоверности и точности измерения НАП.
Технический результат достигается тем, что в способе определения нелинейного акустического параметра твердых, жидких и газообразных сред, включающем излучение в контролируемую среду бигармонической волны, состоящей из гармоник с начальными амплитудами ν01(0), ν02(0) и частотами ω, 2ω, а также прием прошедшей через исследуемую среду волны и выделение второй гармоники, фазовый инвариант излучаемого сигнала выбирают равным ψ = Φ2-2Φ1= π, изменяют амплитуды компонент излучаемого сигнала, сохраняя постоянным отношение A = ν02(0)/ν01(0), где величина A выбирается из диапазона 0 < A < 0,61, до тех пор, пока амплитуда принимаемой второй гармоники в месте расположения приемника станет равной нулю, определяют соответствующую этому условию начальную амплитуду первой гармоники ν01(0) излучаемой волны, после чего по известным скорости звука c0 в исследуемой среде, частоте ω, начальной амплитуде ν01(0) первой гармоники излучаемой волны, расстоянию между приемником и излучателем x определяют НАП по формуле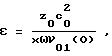
где z0 находят из уравнения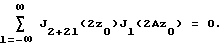
Изобретение соответствует критериям изобретательский уровень, новизна и промышленная применимость, поскольку не обнаружено решений с признаками, отличающими заявляемое техническое решение от прототипа.
Возможность достижения технического результата изобретения подтверждается следующими теоретическими выводами.
Представление о взаимодействии волн ν1 и ν2 с частотами ω и 2ω в нелинейной среде можно получить из решения уравнения Римана для граничного условия в виде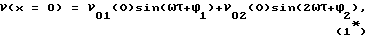
где τ = t - x/c0; t - время; x - координата; c0 - скорость звука; ν01(0), ν02(0) и Φ1,Φ2 - начальные амплитуды и фазы волн ν1 и ν2, соответственно (см. работу: Гаврилов А.M., Савицкий О.А. К вопросу об использовании эффекта вырожденного параметрического усиления. // Акустич. журн., 1992. Т.38, вып. 4. С. 671-677). Решение уравнения Римана при граничном условии (1*) позволяет получить следующие выражения для пространственных распределений амплитуд волн ν1 и ν2
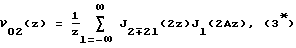
где z = εωxν01(0)/с
Выражения (2*) и (3*) корректно описывают взаимодействие волн в области до образования разрыва в волновом профиле (z < zp), за которой происходит формирование слабых ударных волн. Величина zp находится из выражений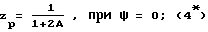

На фиг. 1 приведены зависимости нормированной амплитуды волны ν2 от нормированной координаты z для случаев ψ = 0 и ψ = π при значениях параметра A = 0,2; 0,4; 0,6. Пунктиром обозначена область z ≥ zp. Из фиг.1 видно, что поведение ν02(z) при ψ = 0 и ψ = π качественно различно. Если ψ = 0, то энергия волны основной частоты ω в процессе взаимодействия перекачивается в волну удвоенной частоты 2ω, что приводит к пространственному росту ее амплитуды ν02(z) относительно начального значения ν02(0) и одновременному убыванию амплитуды ν1. Если ψ = π, то имеет место обратный процесс - энергия второй гармоники по мере распространения перекачивается в первую гармонику. Это происходит до тех пор, пока амплитуда второй гармоники не станет равной нулю, что имеет место в точке z0 (точки, z01, z02, z03 на фиг. 1). При этом амплитуда ν1 увеличивается, достигая в точке z0, максимального значения. В области z > z0 начинается процесс генерации второй гармоники волной ν1, в результате чего амплитуда волны ν2 растет с увеличением расстояния, при этом фазовый инвариант уже равен нулю.
Как следует из фиг. 1, при ψ = π в пространственном распределении амплитуды второй гармоники имеется особая точка x = x0. Величина x0 однозначно связана с амплитудами исходных волн, нелинейным параметром и частотой соотношением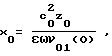
где z0 является корнем уравнения: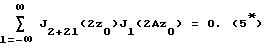
Сохраняя постоянным заданное значение A, одновременным изменением амплитуд ν01(0) и ν02(0) совмещают положение точки минимума амплитуды второй гармоники x0 с местоположением акустического приемника. После этого НАП можно определить по формуле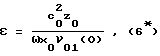
где z0 находится из уравнения (5*); x0 - расстояние между излучателем и приемником акустических волн.
Чтобы измерения проводились в области до точки образования разрыва в волновом профиле, должно соблюдаться условие z0 < zp. Это условие накладывает ограничения на диапазон возможных значений A. Как следует из фиг. 1, увеличение A одновременно приближает точку zp к излучателю и удаляет точку z0. При некотором значении A точки z0 и zp сольются, что соответствует максимально возможному значению A, при котором расчет НАП по формуле (6*) является корректным. Значение Amax можно найти, решая уравнение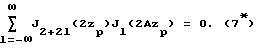
где zp = 16A/(1 + 32A2). Численное решение (7*) дает результат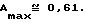
При выполнении условия 0 < A < 0,61 точка нулевого минимума зависимости ν02(z) всегда будет находиться ближе к излучателю, чем точка образования разрыва в волновом профиле, и НАП может быть определен точной формулой (6*).
Процедура определения НАП может быть значительно упрощена при малых значениях A (A << 1). В этом случае можно воспользоваться асимптотическим решением уравнения (5*)
z0 ≈ 2A
и определить НАП непосредственно из выражения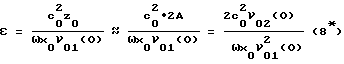
Расчеты показывают, что при A ≅ 0,06 отличие значения z0 = 2A от точного решения уравнения (5*) составляет не более 1%.
В прототипе НАП определяется из (3) с использованием коэффициента амплитудной модуляции m, вычисляемого по измеренным экстремальным значениям амплитуды волны ν02 (Umax и Umin соответственно при ψ = 0 и ψ = π).
Формула (3) в прототипе и приближенное выражение (8*) заявляемого способа (для частного случая A << 1) аналогичны друг другу при условии m = 1. Это условие правомерно, т.к. в заявляемом способе приемник помещен в точку x = x0, где имеет место равенство Umin = 0. Действительно, из (3) следует выражение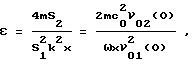
которое при m = 1 и x = x0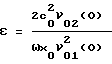
полностью идентично равенству (8*).
Формула (3) следует из точного выражения (3*) при двух допущениях:
1) ν02(z) монотонно убывает при ψ = π и монотонно возрастает при ψ = 0;
2) z << 1 и Az << 1. Измерения НАП в прототипе достоверны только при условии, что приемник расположен на расстоянии x < x0 от излучателя, где осевое распределение амплитуды второй гармоники ν02(z) при ψ = π монотонно убывает. Но без априорной информации о величине НАП невозможно проверить, выполнено ли это условие. Поэтому в прототипе невозможно достоверно определить НАП по измеренным значениям m, S1, S2 и известным x и k (здесь ν02 = 2ωS2), т.к. при расположении приемника в области x ≥ x0 расчет НАП по формуле (3) дает заведомо неверный результат.
Указанный недостаток прототипа в заявляемом способе устраняется тем, что для измерения НАП используется не произвольная точка осевого распределения ν02(z), а точка нулевого минимума амплитуды второй гармоники x = x0, имеющая место при ψ = π. Эта точка всегда единственная и ее координата однозначно связана с величиной НАП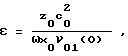
где z0 - корень уравнения (5*). Ограничение 0 < A < 0,61 автоматически обеспечивает корректность расчетных соотношений.
Другим недостатком прототипа является низкая точность определения НАП, обусловленная приближенным характером соотношения, связывающего искомый параметр с измеряемыми величинами. Используемая в прототипе расчетная формула (3) может быть получена из точного выражения (3*) аппроксимацией осевой зависимости ν02(z) в области z < z0 линейными функциями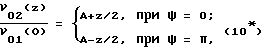
изображенными на фиг. 1 штрихпунктирными линиями. Физически это означает, что в прототипе пренебрегли влиянием на эффективность энергообмена между волнами ν01 и ν02 изменения их амплитуд, произошедшего в результате оттока энергии в высшие гармоники и волны комбинационных частот (2pω±nω), где p, n = 1, 2, 3, ... Как видно из фиг. 1, функция (10*) достаточно точно аппроксимирует реальное распределение амплитуды ν02(z) лишь на небольшом участке, примыкающем к излучателю. С увеличением z и A отклонение (10*) от точного значения (3*) возрастает. Следовательно, определяемое в прототипе значение НАП при любом x ≠ 0 будет содержать неучтенную систематическую погрешность, величина которой тем больше, чем больше расстояние между излучателем и приемником.
В заявляемом техническом решении указанный недостаток устраняется использованием для расчета НАП точных расчетных соотношений (5*) и (6*), учитывающих особенности нелинейного взаимодействия в бигармонической волне конечной амплитуды.
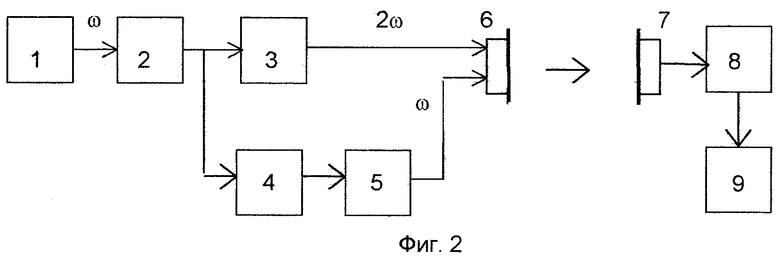
Предлагаемое изобретение поясняется графическими материалами. На фиг. 1 приведены зависимости нормированной амплитуды волны ν2 от безразмерной координаты z для ψ = 0 и ψ = π при значениях параметра A = 0,2; 0,4; 0,6. На фиг. 2 приведена структурная схема устройства, иллюстрирующая возможность технической реализации предлагаемого способа.
Изобретение иллюстрируется примером его конкретного осуществления. На фиг. 2 показана структурная схема устройства, реализующего способ измерения НАП жидких, твердых и газообразных сред. Устройство содержит последовательно включенные генератор синусоидальных колебаний 1 и первый регулируемый усилитель 2, к выходу которого подключены удвоитель частоты 3 и последовательно соединенные второй регулируемый усилитель 4 и фазовращатель 5; выходы удвоителя частоты 3 и фазовращателя 5 подключены к первому и второму входам излучателя 6, последовательно соединенные приемник 7, избирательный усилитель 8 и нуль-индикатор 9. Шкалы регулирующих элементов первого и второго регулируемых усилителей 2 и 4 предварительно проградуированы таким образом, чтобы путем непосредственного отсчета можно было определять амплитуды излучаемых волн ν01(0) и ν02(0).
Работает устройство следующим образом. Генератор 1 вырабатывает синусоидальные электрические колебания частоты ω, подаваемые на первый регулируемый усилитель 2, который предназначен для синхронного изменения амплитуд
излучаемых волн ν01(0) и ν02(0). С выхода первого регулируемого усилителя 2 сигнал поступает на входы удвоителя частоты 3 и второго регулируемого усилителя 4, предназначенного для установки выбранного значения A = ν02(0)/ν01(0). С выхода удвоителя частоты 3 сигнал частоты 2ω поступает на первый вход излучателя, а с выхода второго регулируемого усилителя 4 сигнал частоты ω через фазовращатель 5 поступает на второй вход излучателя 6. Излучатель 6 создает в исследуемой среде поле бегущих акустических волн ν1 и ν2 с частотами ω и 2ω, соответственно. В контролируемой среде, расположенной между излучателем 6 и приемником 7 происходит нелинейное взаимодействие этих волн, после чего они попадают на приемник 7, где преобразуются в электрический сигнал. Сигнал с выхода приемника 7 через избирательный усилитель 8, где происходит выделение и усиление сигнала с частотой 2ω поступает на нуль-индикатор 9. При измерении НАП вторым регулируемым усилителем 4 устанавливают значение A = ν02(0)/ν01(0), находящееся в диапазоне значений 0 < A < 0,61, а фазовращателем 5 устанавливают фазовый инвариант излучаемого сигнала равным ψ = π. Первым регулируемым усилителем 2 синхронно изменяют амплитуды излучаемых волн ν01(0) и ν02(0), добиваясь нулевого показания нуль-индикатора 9. По показаниям первого регулируемого усилителя 2 определяется начальное значение амплитуды 1-й гармоники излучаемого сигнала ν01(0). После этого величина НАП вычисляется по формуле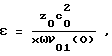
где c0 - скорость звука в среде; x - расстояние между излучателем и приемником; ω - частота волны ν1; z0 - определяется из уравнения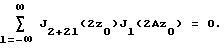
Использование предложенного способа измерения НАП жидких, твердых и газообразных сред позволяет производить достоверные измерения НАП различных сред, существенно повысить точность измерений.
| название | год | авторы | номер документа |
|---|---|---|---|
| МЕТОД ОПРЕДЕЛЕНИЯ НЕЛИНЕЙНОГО АКУСТИЧЕСКОГО ПАРАМЕТРА ЖИДКОСТЕЙ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2013 |
|
RU2532143C1 |
| СПОСОБ АКТИВНОГО ЗВУКОГАШЕНИЯ | 1999 |
|
RU2185666C2 |
| СПОСОБ ПОДАВЛЕНИЯ НЕЛИНЕЙНОГО ПОГЛОЩЕНИЯ ЗВУКА | 1991 |
|
RU2017232C1 |
| ПАРАМЕТРИЧЕСКИЙ ЭХО-ИМПУЛЬСНЫЙ ЛОКАТОР | 1996 |
|
RU2133047C1 |
| АКУСТИЧЕСКИЙ ЭХОЛОКАТОР | 2002 |
|
RU2205421C1 |
| ГЕНЕРАТОР СВЕРХВЫСОКИХ ЧАСТОТ | 1999 |
|
RU2190921C2 |
| ЭХОЛОКАТОР ДЛЯ ПОИСКА ОБЪЕКТОВ ВБЛИЗИ ДНА, НА ДНЕ И В ПРИПОВЕРХНОСТНОМ СЛОЕ ДНА | 1999 |
|
RU2149424C1 |
| АКУСТООПТИЧЕСКИЙ ПРИЕМНИК-ЧАСТОТОМЕР | 2000 |
|
RU2178181C2 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ КОНЦЕНТРАЦИИ СВОБОДНОГО ГАЗА В ЖИДКОСТИ | 1993 |
|
RU2008664C1 |
| УЛЬТРАЗВУКОВАЯ ЛИНИЯ ЗАДЕРЖКИ НА ОБЪЕМНЫХ АКУСТИЧЕСКИХ ВОЛНАХ | 2000 |
|
RU2169429C1 |
Изобретение относится к измерительной технике и может быть использовано для определения физико-механических параметров жидких, твердых и газообразных сред, решения задач медицинской и технической диагностики. Повышение достоверности и точности измерения нелинейного акустического параметра достигается за счет того, что в контролируемую среду излучают бигармоническую волну, состоящую из гармоник с начальными амплитудами ν01(0), ν02(0) колебательной скорости и частотами ω, 2ω, принимают прошедшую через исследуемую среду волну и выделяют вторую гармонику. Фазовый инвариант излучаемого сигнала устанавливают равным π, изменяют амплитуды компонент излучаемого сигнала, сохраняя постоянным параметр А, равный отношению начальной амплитуды второй гармоники ν02(0)к начальной амплитуде первой гармоники ν01(0). Величина А выбирается из диапазона от 0 до 0,61 до тех пор, пока амплитуда принимаемой второй гармоники в месте расположения приемника станет равной нулю. Определяют соответствующую этому условию начальную амплитуду первой гармоники ν01(0) излучаемой волны, рассчитывают нелинейный акустический параметр по формуле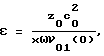
где z0 находится из уравнения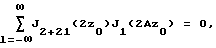
где с0 - скорость звука в исследуемой среде, ν01(0) - начальная амплитуда первой излучаемой гармоники, х - расстояние между излучателем и приемником. 2 ил.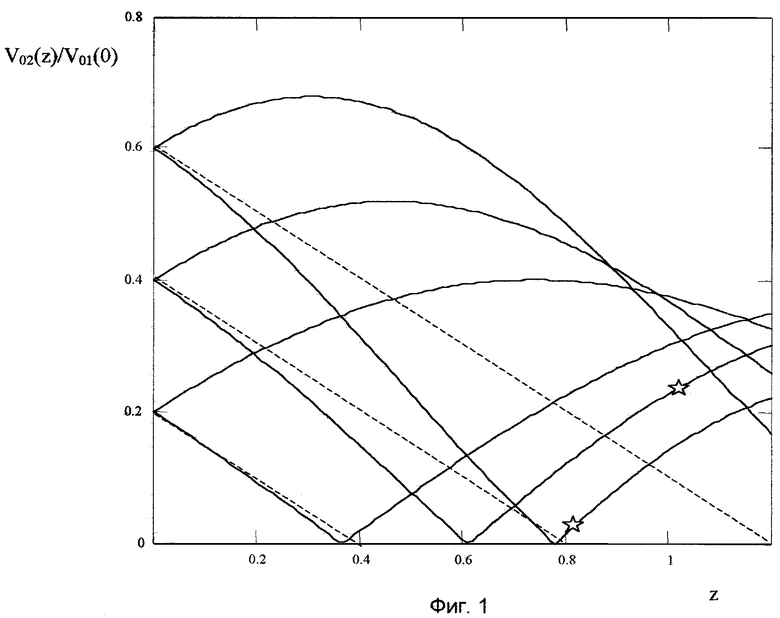
Способ измерения нелинейного акустического параметра жидких, твердых и газообразных сред, заключающийся в том, что в контролируемую среду излучают бигармоническую волну, состоящую из гармоник с начальными амплитудами ν01(0), ν02(0) колебательной скорости и частотами ω, 2ω, принимают прошедшую через исследуемую среду волну и выделяют вторую гармонику, отличающийся тем, что фазовый инвариант излучаемого сигнала устанавливают равным π, изменяют амплитуды компонент излучаемого сигнала, сохраняя постоянным параметр A, равный отношению начальной амплитуды второй гармоники ν02(0) к начальной амплитуде первой гармоники ν01(0), где величина A выбирается из диапазона от 0 до 0,61, до тех пор, пока амплитуда принимаемой второй гармоники в месте расположения приемника станет равной нулю, определяют соответствующую этому условию начальную амплитуду первой гармоники ν01(0) излучаемой волны, рассчитывают нелинейный акустический параметр по формуле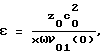
где z0 находится из уравнения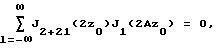
где c0 - скорость звука в исследуемой среде;
ν01(0) - начальная амплитуда первой излучаемой гармоники;
x - расстояние между излучателем и приемником.
Авторы
Даты
2001-06-10—Публикация
1999-03-10—Подача