Изобретение относится к исследованиям физических свойств материалов, преимущественно к анализу вязкоупругих свойств гибких элементов, таких как нити, тросы, кабели и т.п.
В теории вязкоупругих тел временем релаксации τ материала называется отношение его коэффициента вязкости μ к модулю упругости Е. В соответствии с моделью линейной вязкоупругости Кельвина-Фойхта) растяжение гибкого элемента может быть описано следующей зависимостью:
где N - сила натяжения гибкого элемента;
EF - жесткость гибкого элемента на растяжение;
l - длина гибкого элемента в ненапряженном состоянии;
δ- упругое удлинение гибкого элемента;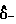 скорость изменения упругого удлинения (точкой здесь и далее обозначается производная по времени);
скорость изменения упругого удлинения (точкой здесь и далее обозначается производная по времени);
τ- время релаксации гибкого элемента.
Время релаксации представляет интерес для анализа затухания колебаний, вызываемого внутренним трением в гибком элементе. Для реальных материалов время релаксации, как правило, не является постоянной величиной, а зависит от условий динамического нагружения, в частности от величины номинальной нагрузки и частоты ее изменения во времени. В связи с этим обстоятельством экспериментальные исследования вязкоупругих свойств рекомендуется проводить в достаточно широких диапазонах условий нагружения испытуемых образцов.
Известен метод статической петли гистерезиса [1, с.318], заключающийся в однократном нагружении и разгружении исследуемого образца с построением зависимости внешней силы от перемещения или напряжения от деформации. По площади петли гистерезиса на графике такой зависимости можно судить о демпфирующих свойствах образца, но только при относительно низких скоростях изменения нагрузки - в диапазоне частот от десятых долей герца и ниже.
Известны также различные методы, предусматривающие циклическое нагружение исследуемого образца с помощью внешнего возбудителя вынужденных колебаний. Метод резонансной кривой [1, с.316-317; 2,3] заключается в получении экспериментальной амплитудно-частотной характеристики, по ширине пика или впадины которой можно определить демпфирующие свойства образца. Метод нарастающих резонансных колебаний [1, с. 317; 2,3] заключается в регистрации процесса нарастания резонансных колебаний при постоянной амплитуде вынуждающей силы. Фазовый метод [1, с.317] заключается в экспериментальном определении угла сдвига фаз между гармоническим возбуждением и вызываемым им перемещением системы при данной частоте возбуждения. Метод максимальной резонансной амплитуды [1, с.318] заключается в измерениии амплитуды вынужденных колебаний системы с частотой, достаточно малой по сравнению с резонансной или примерно в 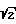 раз большей ее. Энергетический метод [1, с.318] заключается в непосредственном измерении затрат электрической или механической мощности возбудителя на поддержание установившихся колебаний системы. Термический метод [1, с.318] заключается в измерении температуры воды, охлаждающей циклически деформируемый образец. Метод динамической петли гистерезиса [1, с.318-319; 4] заключается в одновременной регистрации сигналов, пропорциональных напряжению (или нагрузке) и деформации (или перемещению) в процессе циклического нагружения образца и получении на этой основе экспериментальной петли гистерезиса, по площади или ширине которой можно определить демпфирующие свойства образца. Эти методы позволяют определить демпфирующие свойства различных конструкционных элементов в достаточно широких диапазонах условий динамического нагружения. Однако такие способы сложны в реализации, так как требуют применения мощных возбудителей вынужденных колебаний, точной измерительной аппаратуры и специальных методов обработки экспериментальных данных. Кроме того, получаемые этими методами экспериментальные данные могут содержать существенные погрешности, вызванные неучитываемым динамическим взаимодействием исследуемого объекта и экспериментальной установки.
раз большей ее. Энергетический метод [1, с.318] заключается в непосредственном измерении затрат электрической или механической мощности возбудителя на поддержание установившихся колебаний системы. Термический метод [1, с.318] заключается в измерении температуры воды, охлаждающей циклически деформируемый образец. Метод динамической петли гистерезиса [1, с.318-319; 4] заключается в одновременной регистрации сигналов, пропорциональных напряжению (или нагрузке) и деформации (или перемещению) в процессе циклического нагружения образца и получении на этой основе экспериментальной петли гистерезиса, по площади или ширине которой можно определить демпфирующие свойства образца. Эти методы позволяют определить демпфирующие свойства различных конструкционных элементов в достаточно широких диапазонах условий динамического нагружения. Однако такие способы сложны в реализации, так как требуют применения мощных возбудителей вынужденных колебаний, точной измерительной аппаратуры и специальных методов обработки экспериментальных данных. Кроме того, получаемые этими методами экспериментальные данные могут содержать существенные погрешности, вызванные неучитываемым динамическим взаимодействием исследуемого объекта и экспериментальной установки.
Наиболее близким аналогом заявляемого изобретения является метод свободных затухающих колебаний [1, с. 315], заключающийся в получении экспериментальных осциллограмм свободных затухающих колебаний механической системы, по темпу убывания амплитуды которых определяют относительное рассеяние энергии или логарифмический декремент колебаний. При исследовании демпфирующих свойств протяженных в одном направлении, в том числе гибких, элементов (стержней, тросов и т.п.) обычно возбуждают свободные продольные (в вертикальном направлении) колебания груза, подвешенного на исследуемом образце [1, с. 319]. Номинальная нагрузка на исследуемый образец будет равна весу подвешенного на нем груза, а частота динамического нагружения - собственной частоте продольных колебаний образца с подвешенным грузом. Для обеспечения чистоты эксперимента требуется уменьшить влияние различных возмущений, в частности по возможности исключить возникновение маятниковых колебаний подвешенного груза. Логарифмический декремент колебаний определяют расчетом по измерениям начальной и конечной амплитуд колебаний и количества совершенных циклов колебаний. Затем по логарифмическому декременту колебаний может быть рассчитано время релаксации исследуемого элемента. Этот способ позволяет исследовать вязкоупругие свойства гибких элементов только в области относительно высоких частот - от нескольких герц и выше.
Техническим результатом заявляемого изобретения является получение дополнительных или уточненных экспериментальных данных о вязкоупругих свойствах гибкого элемента в диапазоне средних частот изменения динамической нагрузки - от десятых долей герца до нескольких герц.
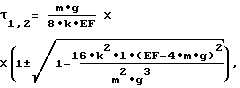
Указанный технический результат достигается тем, что в первом варианте изобретения возбуждают маятниковые колебания подвешенного на исследуемом образце груза в барокамере, измеряют длительность затухания маятниковых колебаний от начальной до конечной амплитуды, два возможных значения времени релаксации гибкого элемента определяют по формуле (2)
(2)
где τ1,2- два возможных значения времени релаксации;
m - масса груза, подвешенного на исследуемом образце;
g - местное ускорение свободного падения;
l - длина исследуемого образца гибкого элемента;
EF - жесткость исследуемого образца на растяжение;
k - параметр, определяющий темп затухания маятниковых колебаний, вычисляемый по формуле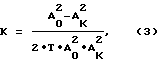
где А0 - начальная амплитуда маятниковых колебаний;
Ак - конечная амплитуда маятниковых колебаний;
Т - длительность затухания маятниковых колебаний от начальной до конечной амплитуды,
истинное значение времени релаксации выбирают из его двух возможных значений с учетом априорной информации о вязкоупругих свойствах гибкого элемента.
Во втором варианте изобретения возбуждают маятниковые колебания подвешенного на исследуемом образце груза в барокамере и оценивают темп затухания маятниковых колебаний, повторяют предыдущие операции для разных длин исследуемого образца и определяют длину образца, при которой темп затухания имеет максимум, время релаксации гибкого элемента определяют по формуле
где τ- время релаксации гибкого элемента;
l* - длина исследуемого образца, при которой темп затухания колебаний имеет максимум;
g - местное ускорение свободного падения.
Сущность изобретения поясняется чертежом, где показаны:
1 - барокамера;
2 - исследуемый образец;
3 - груз;
4 - измерительная шкала.
В барокамере 1 на исследуемом образце 2 подвешивается груз 3, барокамера 1 вакуумируется и возбуждаются маятниковые колебания груза 3 на исследуемом образце 2. Амплитуда маятниковых колебаний может измеряться с помощью измерительной шкалы 4, а текущее время - по часам. Темп затухания маятниковых колебаний может оцениваться визуально, с помощью кино- или видеосъемки и т.п.
В процессе маятниковых колебаний груза 3 возникают вынужденные продольные колебания исследуемого образца 2, частота которых равна удвоенной частоте маятниковых колебаний. В процессе продольных колебаний происходит рассеивание энергии вследствие внутреннего трения в исследуемом образце 2. Вследствие этого уменьшается амплитуда как продольных, так и маятниковых колебаний груза 3, подвешенного на исследуемом образце 2. Для исключения влияния на этот процесс сопротивления атмосферы исследования необходимо проводить в вакуумированной барокамере 1.
Темп затухания маятниковых колебаний определяется вязкоупругими свойствами исследуемого образца 2, следовательно, по наблюдаемому процессу можно судить о величине времени релаксации гибкого элемента. При этом номинальной нагрузкой можно считать вес груза 3, а частотой изменения динамической нагрузки - частоту продольных колебаний. Для длин исследуемого образца 2 от 0,1 до 10 м эта частота будет находиться в диапазоне от 0,3 до 3 Гц. Таким образом, проводя исследования для разных длин исследуемого образца 2 и разных масс груза 3, можно построить зависимость времени релаксации гибкого элемента в определенных областях номинальных нагрузок и частот колебаний.
Формулы для расчета времени релаксации получаются из анализа математического описания продольно-маятниковых колебаний груза 3, подвешенного на исследуемом образце 2 гибкого элемента, вязкоупругие свойства которого описываются зависимостью (1). Движение такой динамической системы описывается следующими дифференциальными уравнениями:
где ϕ- текущий угол отклонения исследуемого образца 2 от вертикали.
Изменение амплитуды маятниковых колебаний груза 3 на исследуемом образце 2 можно приближенно описать дифференциальным уравнением
где А - амплитуда маятниковых колебаний;
k - параметр, определяющий темп затухания маятниковых колебаний, рассчитываемый по формуле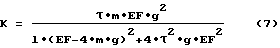
или по эквивалентной ей формуле
где р и q - круговые частоты соответственно маятниковых и продольных колебаний груза 3 на исследуемом образце 2, вычисляемые по формулам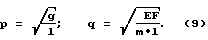
Из формулы (7) следует, что зависимость параметра к от времени релаксации τ немонотонная, то есть одному значению к соответствуют два возможных значения τ (см. формулу (2)). Это означает, что процесс затухания маятниковых колебаний может иметь один и тот же вид при двух разных значениях времени релаксации. Увеличение времени релаксации до определенной критической величины приводит к повышению темпа затухания маятниковых колебаний, а затем - к его снижению. Значение параметра к и, соответственно, темп затухания маятниковых колебаний будут иметь максимум при величине времени релаксации, равной
Поскольку для реальных гибких элементов, как правило, жесткость на растяжение намного превышает разрывную нагрузку, можно считать, что EF>m•g. Следовательно, формулу (10) можно записать в приближенном виде
то есть темп затухания маятниковых колебаний будет иметь максимум в случае, когда время релаксации гибкого элемента в 4π раз меньше периода маятниковых колебаний. Из формулы (11) следует, что существует определенная длина l* исследуемого образца 2, при которой темп затухания маятниковых колебаний имеет максимум. Определив эту длину, можно по формуле (4) вычислить время релаксации гибкого элемента.
Для малых маятниковых колебаний дифференциальное уравнение (6) можно приближенно записать в виде уравнения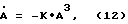
которое имеет аналитическое решение
где А0 - начальная амплитуда маятниковых колебаний;
t - время, отсчитываемое от начала колебаний.
Численные исследования показывают, что аналитическое решение (13) достаточно точно согласуется с численным решением уравнения (6), которое в свою очередь хорошо согласуется с численным решением уравнений (5). Если за время Т амплитуда маятниковых колебаний уменьшается от начального значения А0 до конечного значения Ак, то в соответствии с (13) параметр сможет быть вычислен по формуле (3).
В первом варианте способа определения времени релаксации гибкого вязкоупругого элемента один сеанс измерений позволяет определить два возможных значения времени релаксации, причем для их расчета по формулам (2) и (3) необходимо знать такую величину, как жесткость гибкого элемента на растяжения. Кроме того, для выбора истинного значения времени релаксации гибкого элемента необходимо иметь какую-либо априорную ориентировочную информацию о его вязкоупругих свойствах. В то же время дополнительные сеансы измерений с варьированием массы груза 3 и длины исследуемого образца 2 позволяют построить зависимость времени релаксации от номинальной величины динамической нагрузки и частоты ее изменения.
Во втором варианте способа необходимо выполнить несколько сеансов измерений с варьированием длины исследуемого образца 2 гибкого элемента. Определив длину исследуемого образца 2, при которой темп затухания маятниковых колебаний имеет максимум, можно по формуле (4) однозначно вычислить время релаксации, причем для этого не требуется какой-либо дополнительной информации о вязкоупругих свойствах гибкого элемента. В то же время этот способ не позволяет построить зависимость времени релаксации от частоты динамического нагружения.
Представляется, что выполнение исследований с использованием обоих предлагаемых вариантов позволит получить достаточно полные, однозначные и точные сведения о вязкоупругих свойствах гибкого элемента.
Литература
1. Машиностроение. Энциклопедия. Ред. совет: К.В. Фролов (пред.) и др. - М. : Машиностроение / Динамика и прочность машин. Теория механизмов и машин. Т. 1-3. В 2-х кн. Кн.2 / А.В. Александров, Н.А. Алфутов, В.В. Астанин и др.; Под общ. ред. К.С. Колесникова. - 1995. 624 с., ил.
2. Матвеев В.В. Демпфирование колебаний деформируемых тел. Киев: Наук. думка, 1985. - 264 с.
3. Писаренко Г.С., Яковлев А.П., Матвеев В.В. Вибропоглощающие свойства конструкционных материалов: Справочник. - Киев: Наук. думка, 1971. - 375 с.
4. Трошенко В.Т. Усталость и неупругость металлов. - Киев: Наук. думка, 1971. - 268 с.
Изобретение относится к исследованиям физических свойств материалов, преимущественно к анализу вязкоупругих свойств гибких элементов. Способ определения времени релаксации гибкого вязкоупругого элемента по первому варианту заключается в подвешивании груза на исследуемом образце элемента в барокамере, возбуждении его маятниковых колебаний с измерением длительности затухания от начальной до конечной амплитуды, а также самих значений амплитуды. Два возможных значения времени релаксации гибкого элемента определяют расчетным путем, а истинное значение времени релаксации выбирают из его двух возможных значений с учетом априорной информации о вязкоупругих свойствах гибкого элемента. Способ определения времени релаксации гибкого вязкоупругого элемента по второму варианту заключается в подвешивании груза на исследуемом образце элемента в барокамере, возбуждении его маятниковых колебаний и оценивании темпа затухания маятниковых колебаний. Затем повторяют предыдущие операции для разных длин исследуемого образца и определяют длину образца, при которой темп затухания имеет максимум, а время релаксации гибкого элемента определяют расчетным путем. Данное изобретение направлено на получение дополнительных или уточненных экспериментальных данных о вязкоупругих свойствах гибкого элемента в диапазоне средних частот изменения динамической нагрузки. 2 с.п. ф-лы, 1 ил.
где τ1,2 - два возможных значения времени релаксации;
m - масса груза, подвешенного на исследуемом образце;
g - местное ускорение свободного падения;
l - длина исследуемого образца гибкого элемента;
EF - жесткость исследуемого образца на растяжение;
k - параметр, определяющий темп затухания маятниковых колебаний, вычисляемый по формуле
где А0 - начальная амплитуда маятниковых колебаний;
Ак - конечная амплитуда маятниковых колебаний;
Т - длительность затухания маятниковых колебаний от начальной до конечной амплитуды,
истинное значение времени релаксации выбирают из его двух возможных значений с учетом априорной информации о вязкоупругих свойствах гибкого элемента.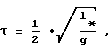
где τ - время релаксации гибкого элемента;
l* - длина исследуемого образца, при которой темп затухания колебаний имеет максимум;
g - местное ускорение свободного падения.
| Динамика и прочность машин | |||
| Теория механизмов и машин./Под ред | |||
| КОЛЕСНИКОВА К.С | |||
| кн | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| - М.: Машиностроение, 1995, с.315 | |||
| СПОСОБ ПОЛИМЕРНОГО БАЛЬЗАМИРОВАНИЯ АНАТОМИЧЕСКИХ ПРЕПАРАТОВ СИЛОКСАНОВЫМИ КОМПОЗИЦИЯМИ | 2009 |
|
RU2426311C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НЕИСПРАВНОЙ СВЕЧИ В ДВИГАТЕЛЕ ВНУТРЕННЕГО СГОРАНИЯ И УСТРОЙСТВО ДЛЯ РЕАЛИЗАЦИИ СПОСОБА | 1997 |
|
RU2146772C1 |
| Способ прогнозирования времени длительной прочности материалов | 1987 |
|
SU1422082A1 |
| GB 1123213 А, 14.08.1968 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ ЗОНЫ И МЕСТА ЗАМЫКАНИЯ ЛИНИИ ЭЛЕКТРОПЕРЕДАЧИ | 1992 |
|
RU2073876C1 |
Авторы
Даты
2002-02-27—Публикация
2000-04-17—Подача